Large-Sized Multirotor Design: Accurate Modeling with Aerodynamics and Optimization for Rotor Tilt Angle
Abstract
:1. Introduction
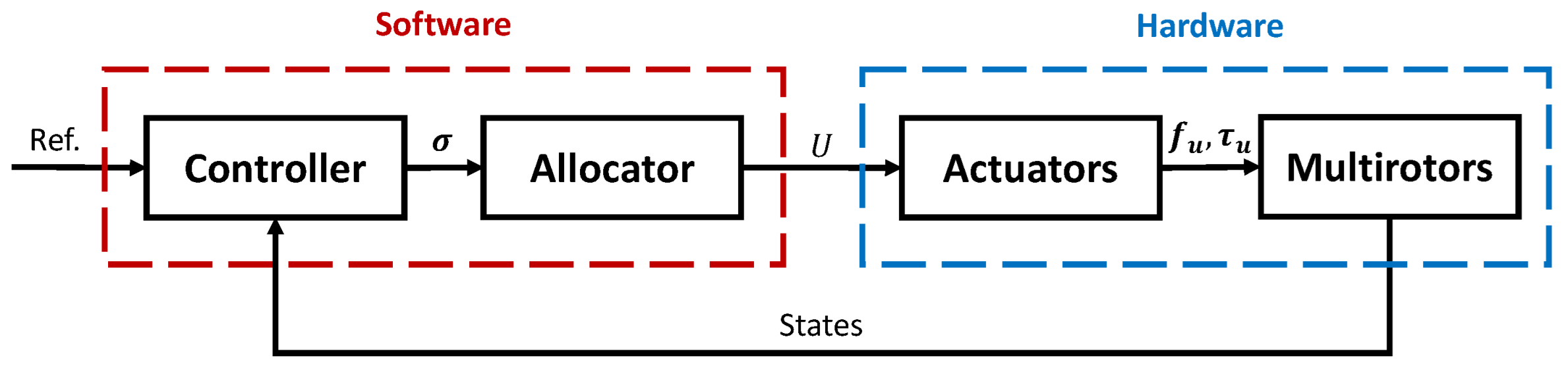
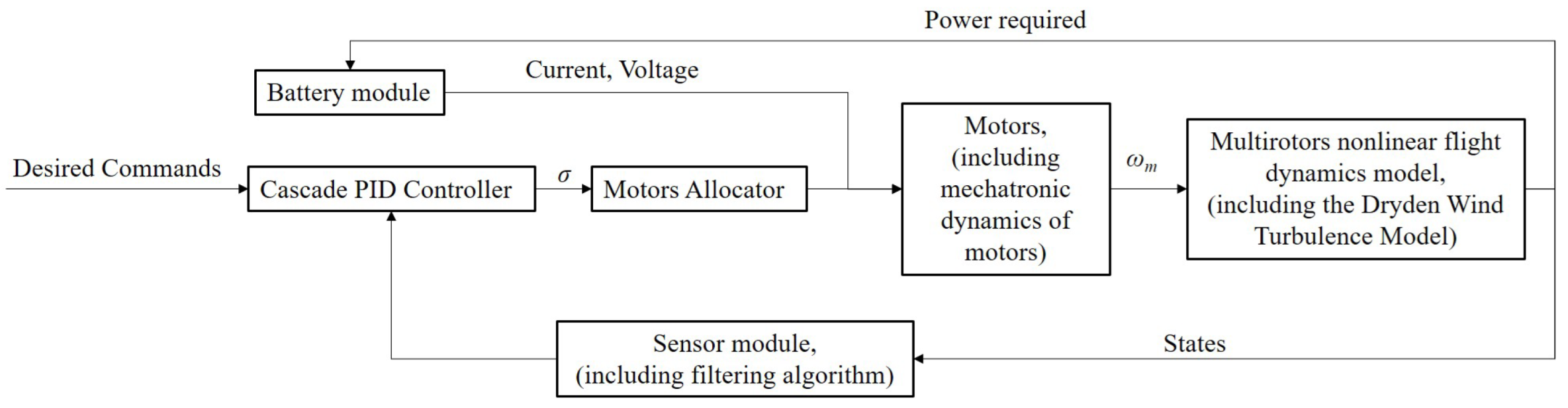
2. System Modeling
2.1. Rigid-Body Dynamics
2.2. Aerodynamics
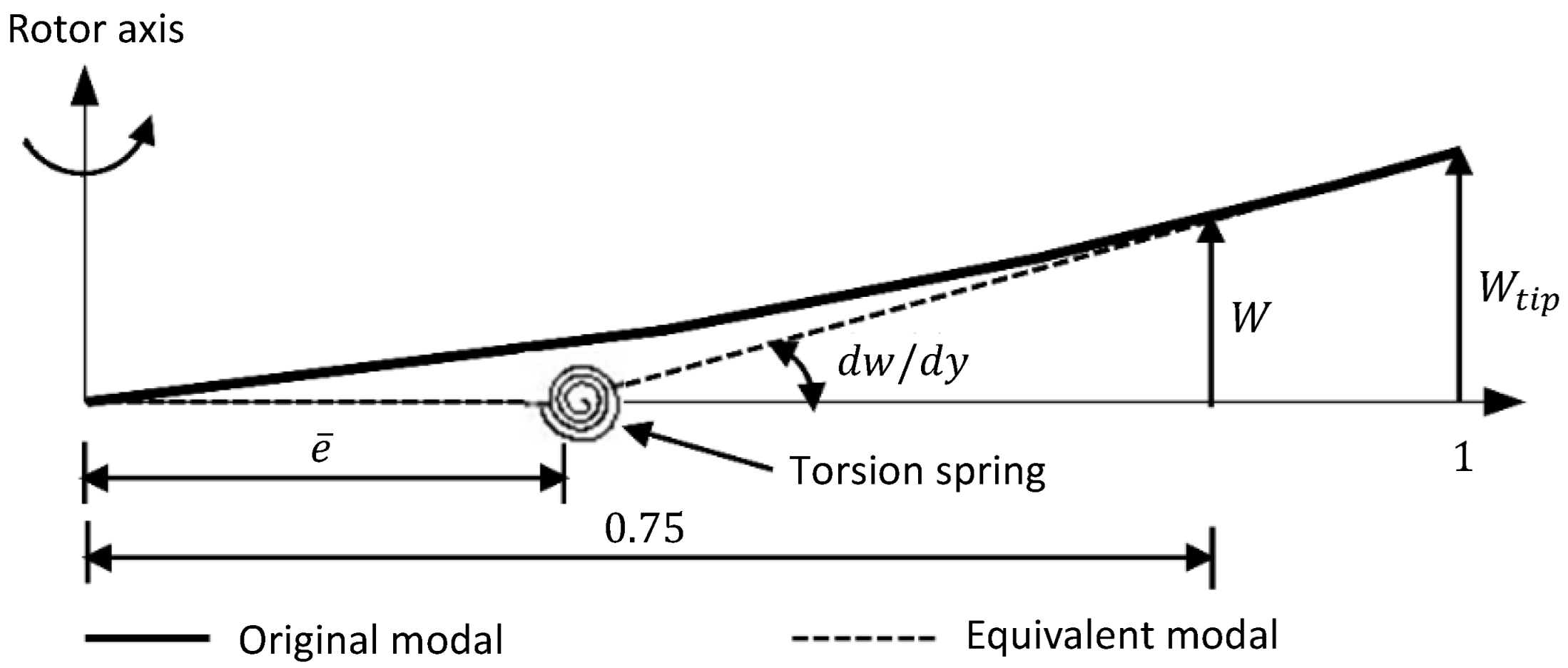
2.2.1. Blade Flapping
2.2.2. Propeller Aerodynamics
2.2.3. Airframe Aerodynamics
2.3. Actuator Dynamics
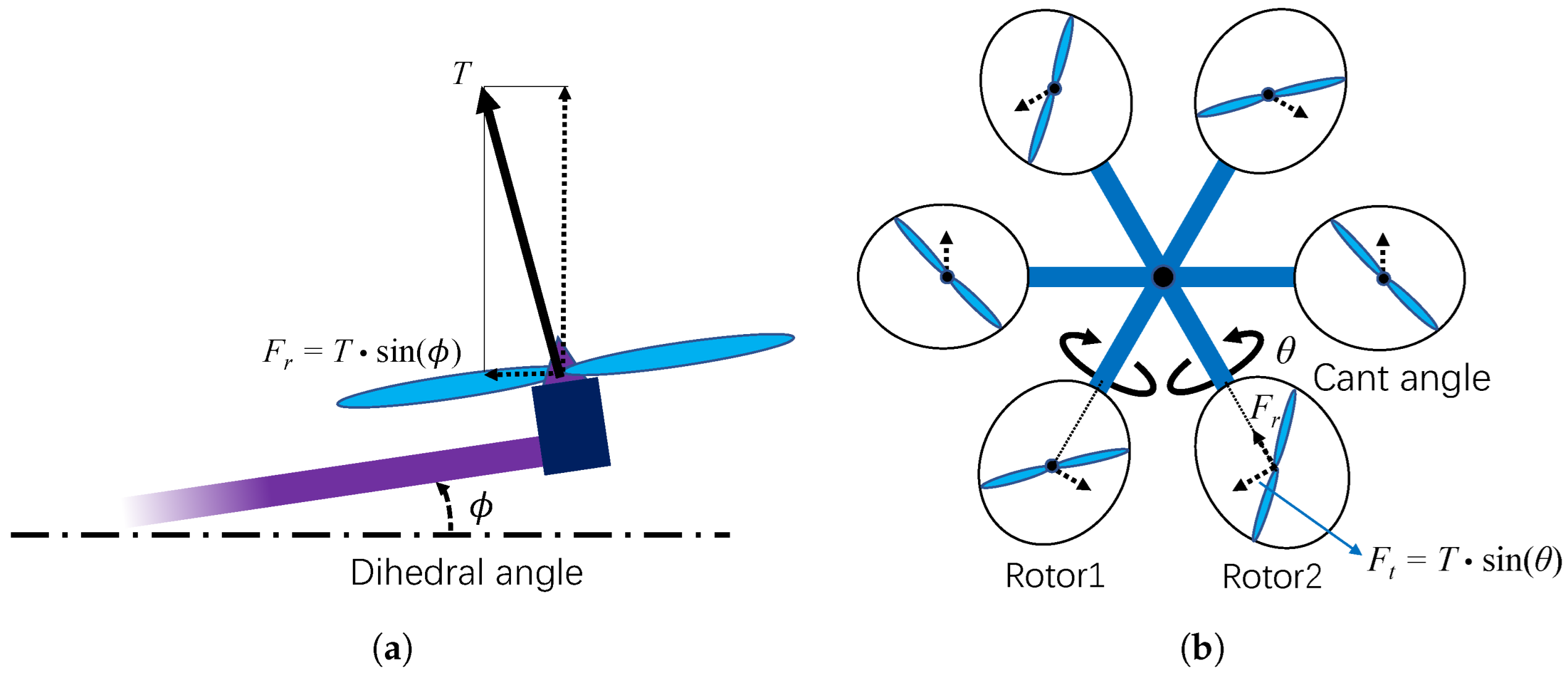
3. Rotor Tilt Angle Design
3.1. Motivation and Purpose
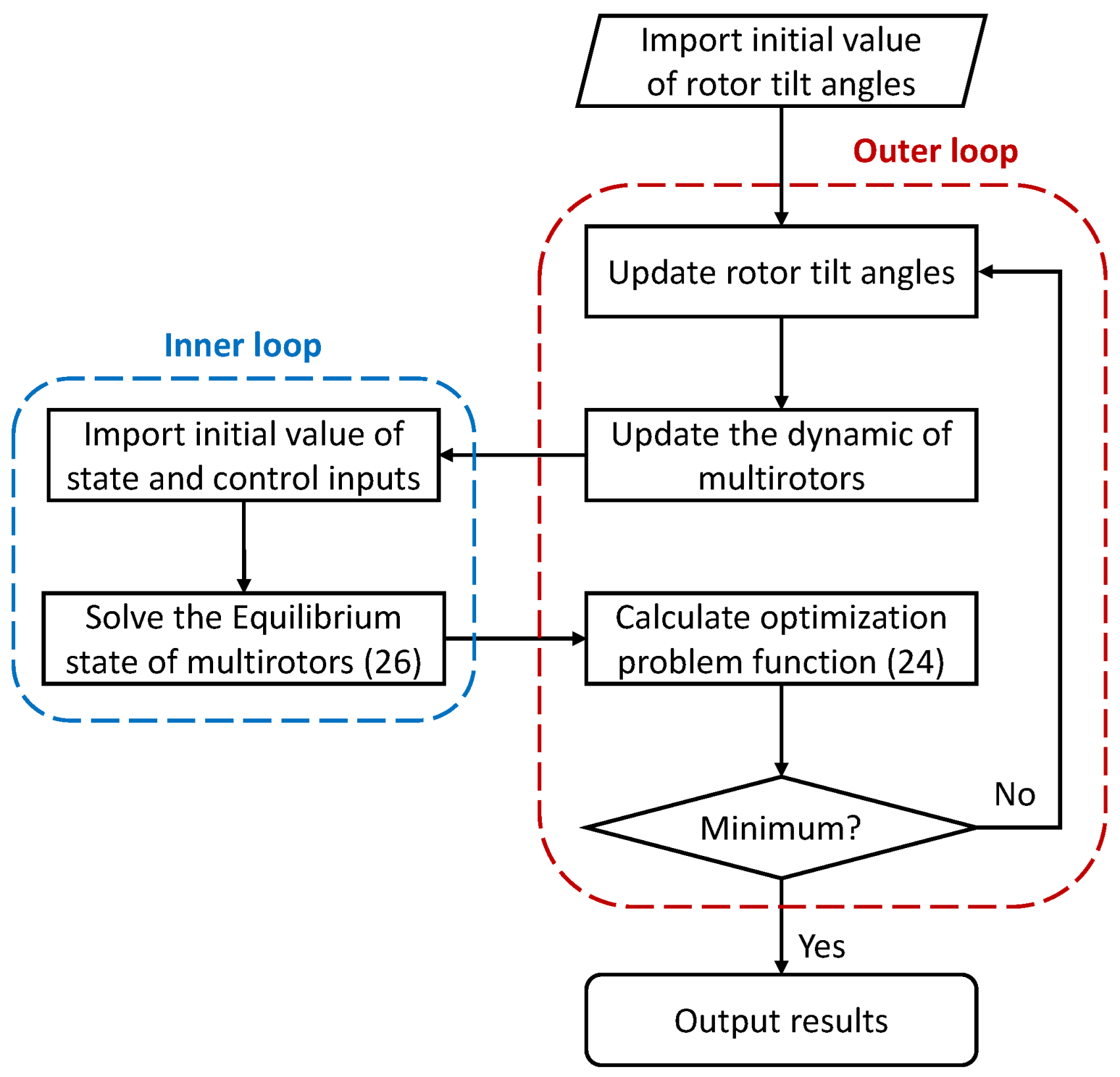
3.2. Optimization Method
4. Experimental Verification
4.1. Model Verification
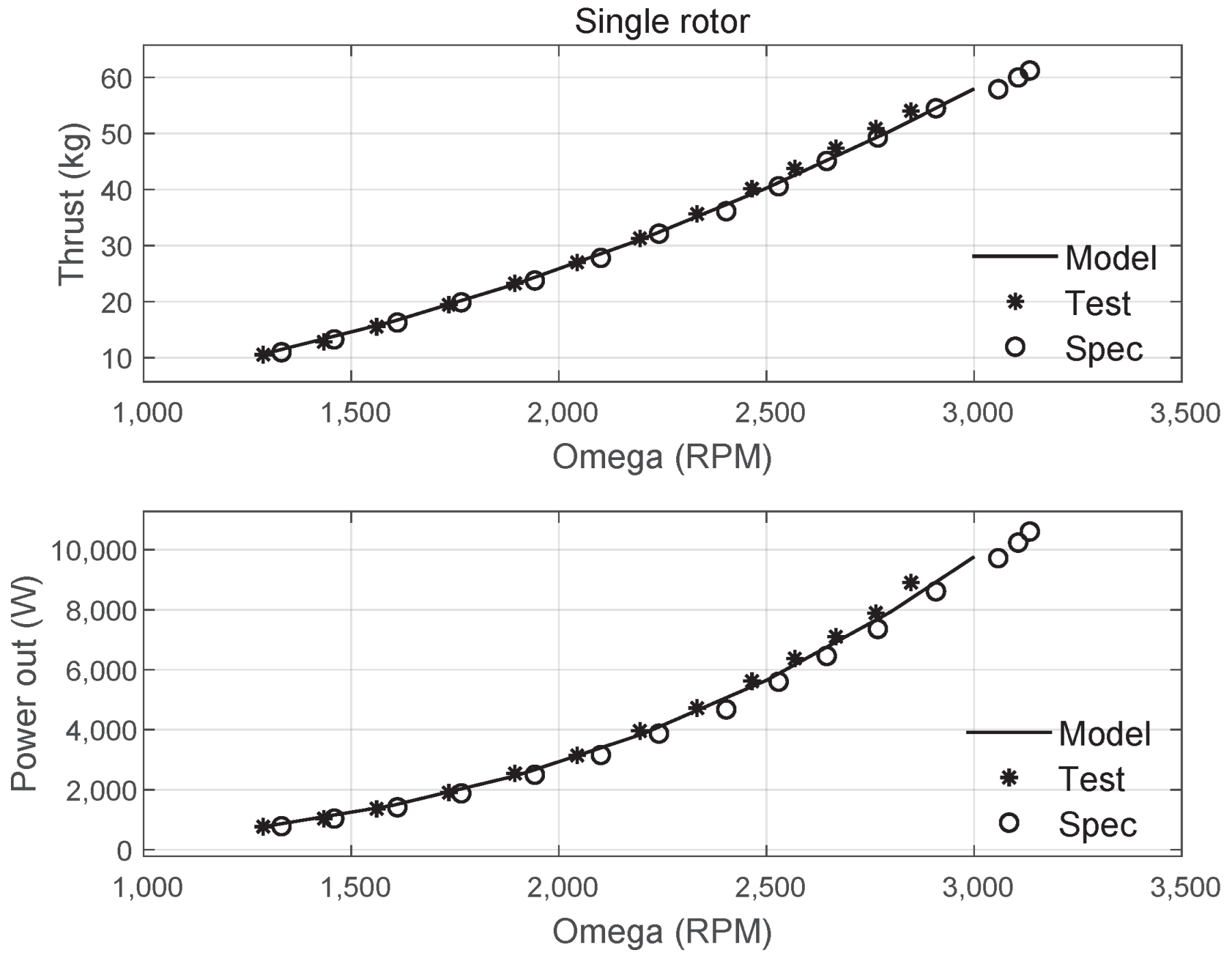
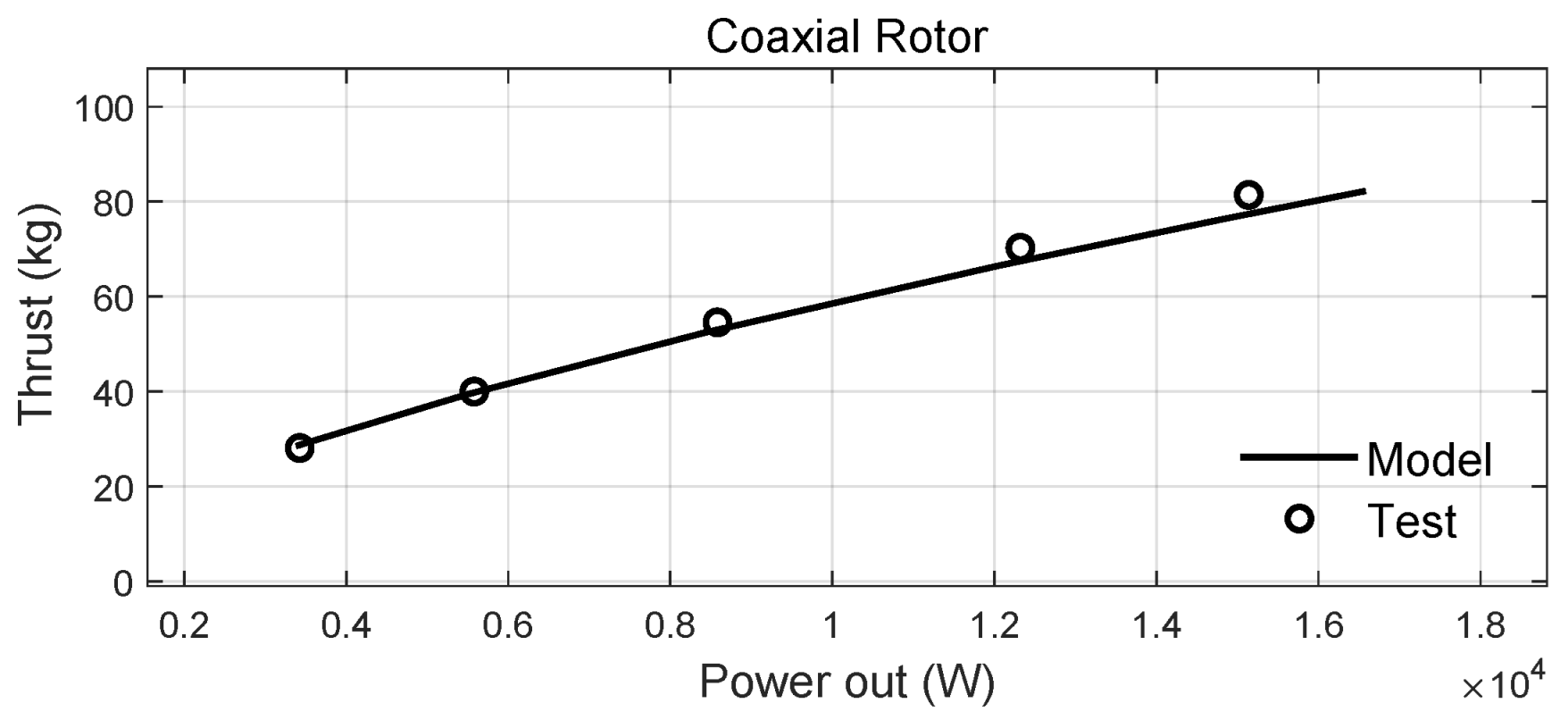
4.1.1. Rotor Tests
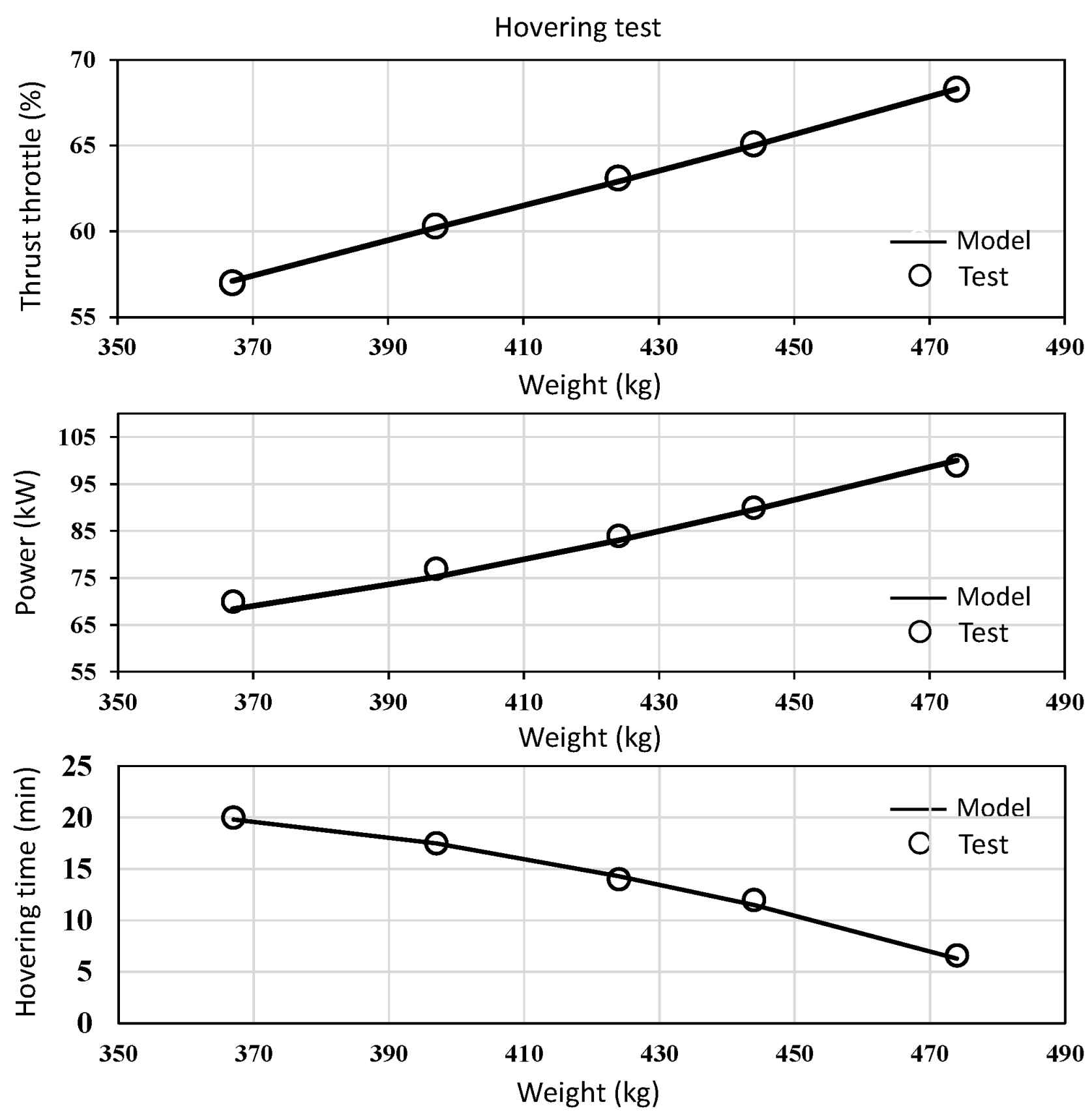
4.1.2. Multirotor Tests
4.2. Design Verification
4.2.1. Preliminary Design in Simulation
4.2.2. Offline Design Optimization
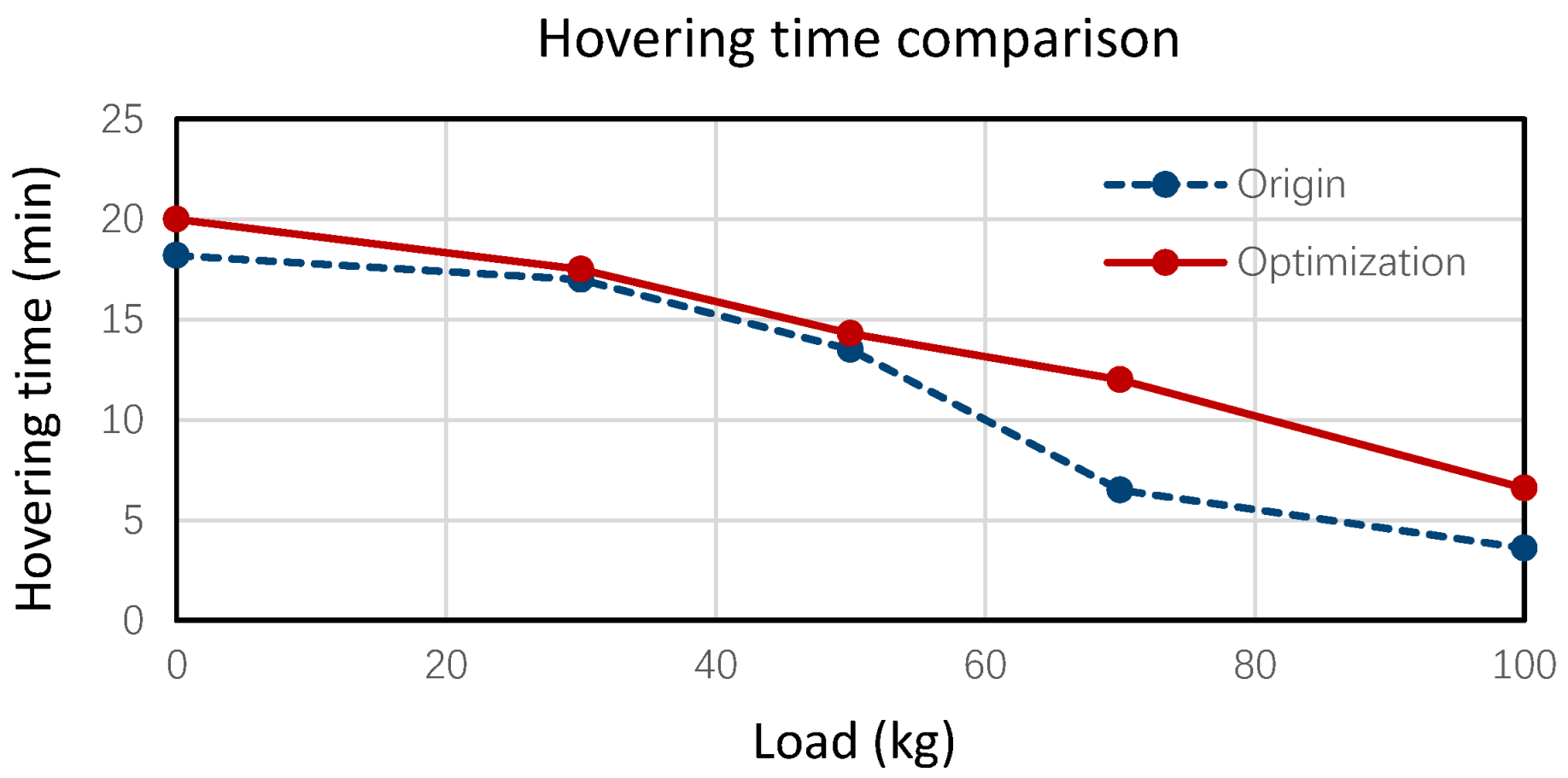
4.2.3. Experimental Design Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Coluccia, A.; Parisi, G.; Fascista, A. Detection and classification of multirotor drones in radar sensor networks: A review. Sensors 2020, 20, 4172. [Google Scholar] [CrossRef]
- Yao, W.; Chen, Y.; Fu, J.; Qu, D.; Wu, C.; Liu, J.; Sun, G.; Xin, L. Evolutionary utility prediction matrix-based mission planning for unmanned aerial vehicles in complex urban environments. IEEE Trans. Intell. Veh. 2022, 8, 1068–1080. [Google Scholar] [CrossRef]
- Rodríguez Marco, J.E.; Sánchez Rubio, M.; Martínez Herráiz, J.J.; González Armengod, R.; Del Pino, J.C.P. Contributions to Image Transmission in Icing Conditions on Unmanned Aerial Vehicles. Drones 2023, 7, 571. [Google Scholar] [CrossRef]
- Villa, D.K.; Brandao, A.S.; Sarcinelli-Filho, M. A survey on load transportation using multirotor UAVs. J. Intell. Robot. Syst. 2020, 98, 267–296. [Google Scholar] [CrossRef]
- Kotarski, D.; Piljek, P.; Kasać, J. Design considerations for autonomous cargo transportation multirotor UAVs. In Self-Driving Vehicles and Enabling Technologies; IntechOpen: London, UK, 2020. [Google Scholar]
- Day, D. Advancing Aerial Mobility: A National Blueprint; National Academies Press: Washington, DC, USA, 2021. [Google Scholar]
- Ploetner, K.; Al Haddad, C.; Antoniou, C.; Frank, F.; Fu, M.; Kabel, S.; Llorca, C.; Moeckel, R.; Moreno, A.; Pukhova, A.; et al. Long-term application potential of urban air mobility complementing public transport: An upper Bavaria example. CEAS Aeronaut. J. 2020, 11, 991–1007. [Google Scholar] [CrossRef]
- Hamilton, B.A. Urban air mobility market study. In Presentation to NASA Aeronautics Research Mission Directorate; NASA: Washington, DC, USA, 2018. [Google Scholar]
- Rashad, R.; Goerres, J.; Aarts, R.; Engelen, J.B.; Stramigioli, S. Fully actuated multirotor UAVs: A literature review. IEEE Robot. Autom. Mag. 2020, 27, 97–107. [Google Scholar] [CrossRef]
- Tadokoro, Y.; Ibuki, T.; Sampei, M. Maneuverability analysis of a fully-actuated hexrotor UAV considering tilt angles and arrangement of rotors. IFAC-PapersOnLine 2017, 50, 8981–8986. [Google Scholar] [CrossRef]
- de Angelis, E.L. Stability analysis of a multirotor vehicle hovering condition. Aerosp. Sci. Technol. 2018, 72, 248–255. [Google Scholar] [CrossRef]
- Mehmood, H.; Nakamura, T.; Johnson, E.N. A maneuverability analysis of a novel hexarotor UAV concept. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016; pp. 437–446. [Google Scholar]
- Bershadsky, D.; Haviland, S.; Johnson, E.N. Electric multirotor UAV propulsion system sizing for performance prediction and design optimization. In Proceedings of the 57th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, San Diego, CA, USA, 4–8 January 2016; p. 0581. [Google Scholar]
- Biczyski, M.; Sehab, R.; Whidborne, J.F.; Krebs, G.; Luk, P. Multirotor sizing methodology with flight time estimation. J. Adv. Transp. 2020, 2020, 9689604. [Google Scholar] [CrossRef]
- Dai, X.; Quan, Q.; Ren, J.; Cai, K.Y. An analytical design-optimization method for electric propulsion systems of multicopter UAVs with desired hovering endurance. IEEE/ASME Trans. Mechatron. 2019, 24, 228–239. [Google Scholar] [CrossRef]
- Liscouët, J.; Pollet, F.; Jézégou, J.; Budinger, M.; Delbecq, S.; Moschetta, J.M. A methodology to integrate reliability into the conceptual design of safety-critical multirotor unmanned aerial vehicles. Aerosp. Sci. Technol. 2022, 127, 107681. [Google Scholar] [CrossRef]
- Dai, X.; Quan, Q.; Cai, K.Y. Design Automation and Optimization Methodology for Electric Multicopter Unmanned Aerial Robots. IEEE Trans. Autom. Sci. Eng. 2021, 19, 2354–2368. [Google Scholar] [CrossRef]
- Jiang, G.; Voyles, R.; Sebesta, K.; Greiner, H. Estimation and optimization of fully-actuated multirotor platform with nonparallel actuation mechanism. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 6843–6848. [Google Scholar]
- Franz, H.; Michael, T. System Design for Uncertainty; Massachusetts Institute of Technology: Cambridge, MA, USA, 2010; Chapter 10; pp. 73–82. [Google Scholar]
- Ding, C.; Wang, C.; Lu, L.; Ouyang, B. Modeling and control of fully actuated vector thrust unmanned aerial vehicles. In Proceedings of the International Symposium on Flexible Automation 2018 International Symposium on Flexible Automation; The Institute of Systems, Control and Information Engineers: Kanazawa, Japan, 2018; pp. 451–458. [Google Scholar]
- Phang, S.K.; Li, K.; Wang, F.; Chen, B.M.; Lee, T.H. Explicit model identification and control of a micro aerial vehicle. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014; pp. 1048–1054. [Google Scholar]
- Bouabdallah, S.; Siegwart, R. Backstepping and sliding-mode techniques applied to an indoor micro quadrotor. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 2247–2252. [Google Scholar]
- Sun, S.; de Visser, C.C.; Chu, Q. Quadrotor gray-box model identification from high-speed flight data. J. Aircr. 2019, 56, 645–661. [Google Scholar] [CrossRef]
- Lei, Y.; Cheng, M. Aerodynamic performance of a Hex-rotor unmanned aerial vehicle with different rotor spacing. Meas. Control 2020, 53, 711–718. [Google Scholar] [CrossRef]
- Yao, L.; Cheng, M. Aerodynamic performance of hex-rotor UAV considering the horizontal airflow. Appl. Sci. 2019, 9, 4797. [Google Scholar]
- Abbaraju, P.; Ma, X. Aerodynamic Modeling of Fully-Actuated Multirotor UAVs with Nonparallel Actuators. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 9639–9645. [Google Scholar]
- Ji, H.; Chen, R.; Li, P. Rotor-state feedback control design to improve helicopter turbulence alleviation in hover. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 232, 156–168. [Google Scholar] [CrossRef]
- Ji, H.; Chen, R. Real-time simulation model for helicopter flight task analysis in turbulent atmospheric environment. Aerosp. Sci. Technol. 2019, 92, 289–299. [Google Scholar] [CrossRef]
- Yuan, Y.; Thomson, D.; Chen, R. Investigation of lift offset on flight dynamics characteristics for coaxial compound helicopters. J. Aircr. 2019, 56, 2210–2222. [Google Scholar] [CrossRef]
- Ferguson, K.; Thomson, D. Flight dynamics investigation of compound helicopter configurations. J. Aircr. 2015, 52, 156–167. [Google Scholar] [CrossRef]
- Ferguson, K.M. Towards a Better Understanding of the Flight Mechanics of Compound Helicopter Configurations. Ph.D. Thesis, University of Glasgow, Glasgow, UK, 2015. [Google Scholar]
- Meier, L.; Honegger, D.; Pollefeys, M. PX4: A node-based multithreaded open source robotics framework for deeply embedded platforms. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 6235–6240. [Google Scholar]
- Lee, T.; Leok, M.; McClamroch, N.H. Geometric tracking control of a quadrotor UAV on SE (3). In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010; pp. 5420–5425. [Google Scholar]
- Gill, P.E.; Murray, W.; Saunders, M.A. SNOPT: An SQP algorithm for large-scale constrained optimization. SIAM Rev. 2005, 47, 99–131. [Google Scholar] [CrossRef]



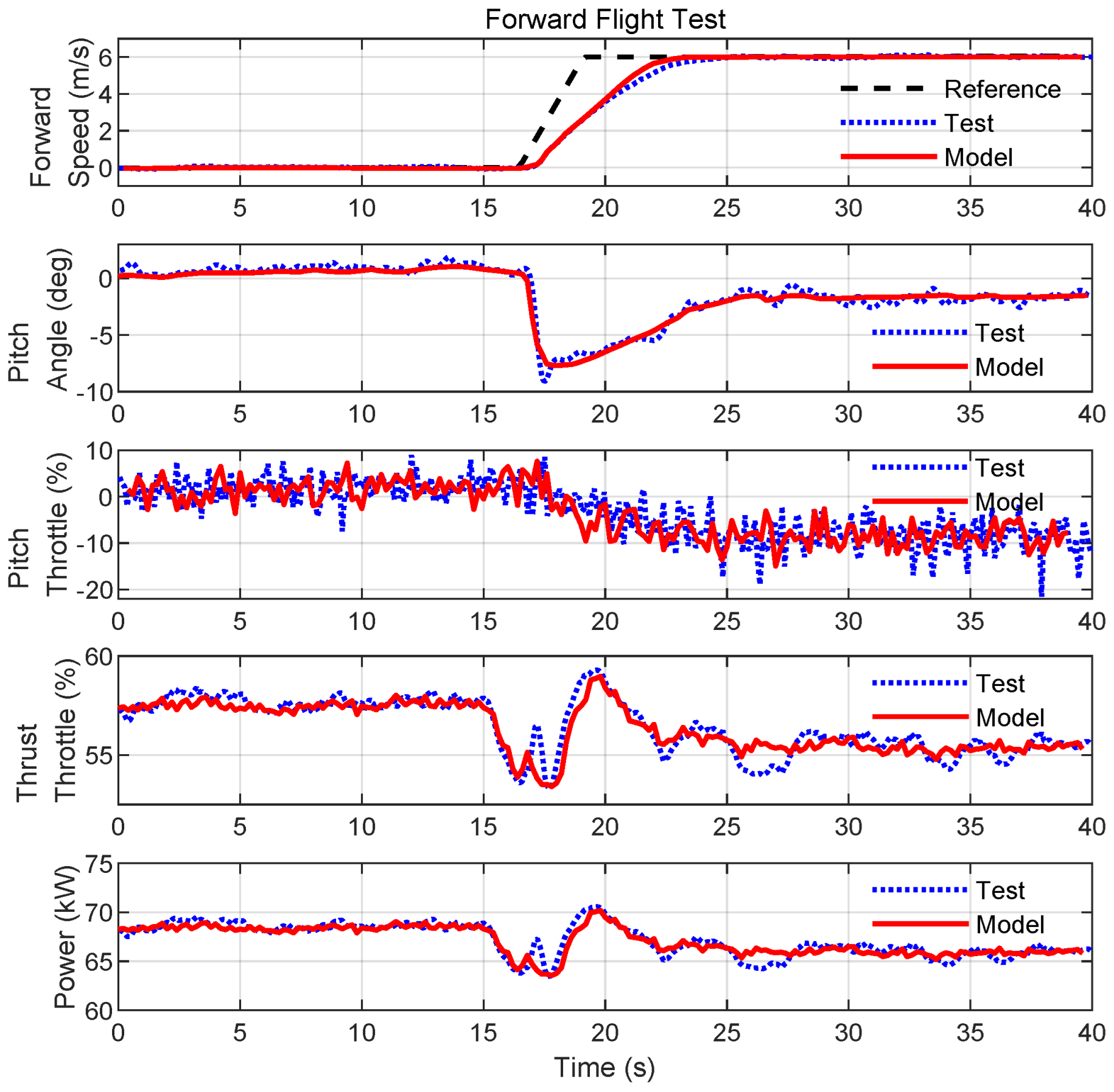
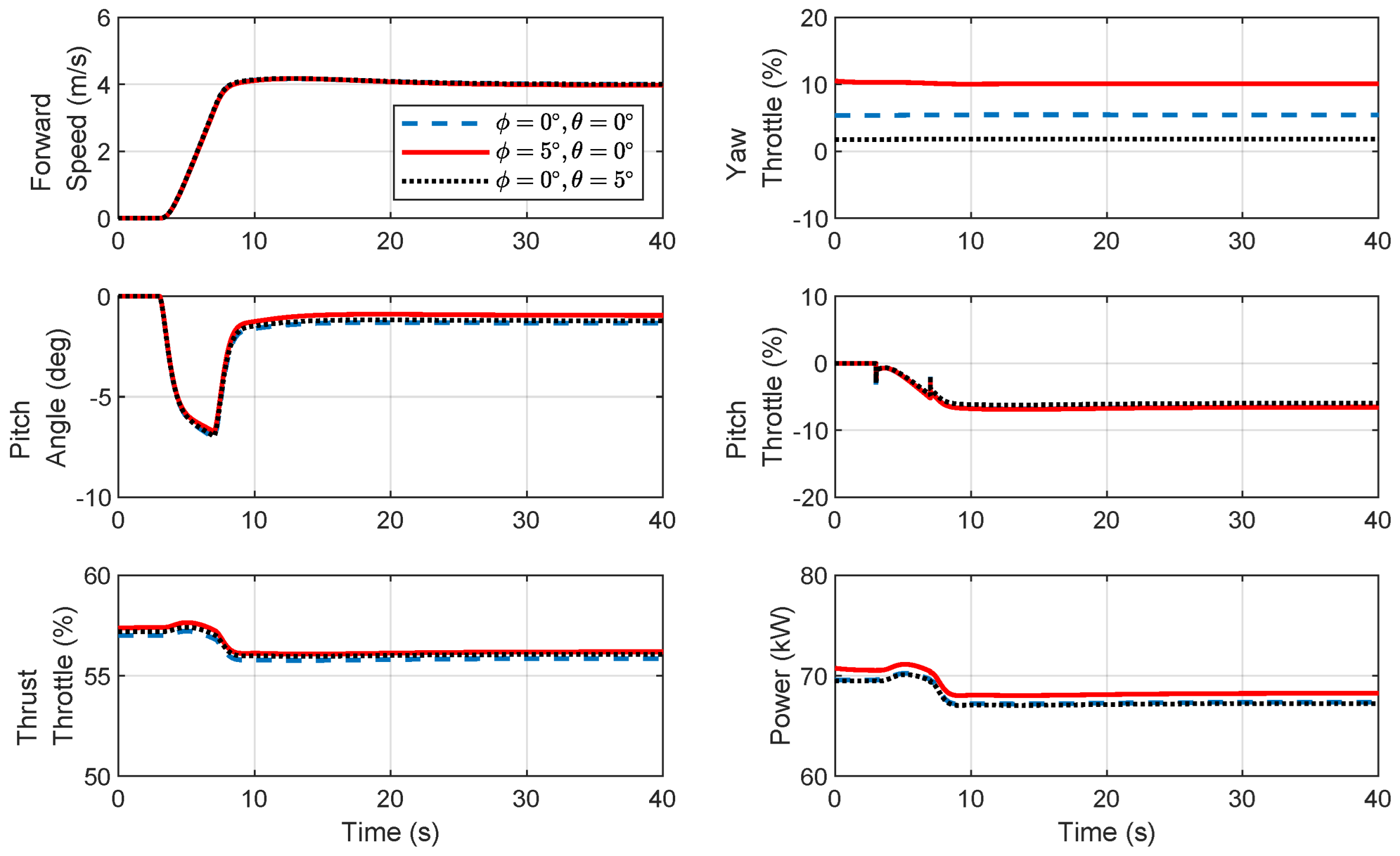


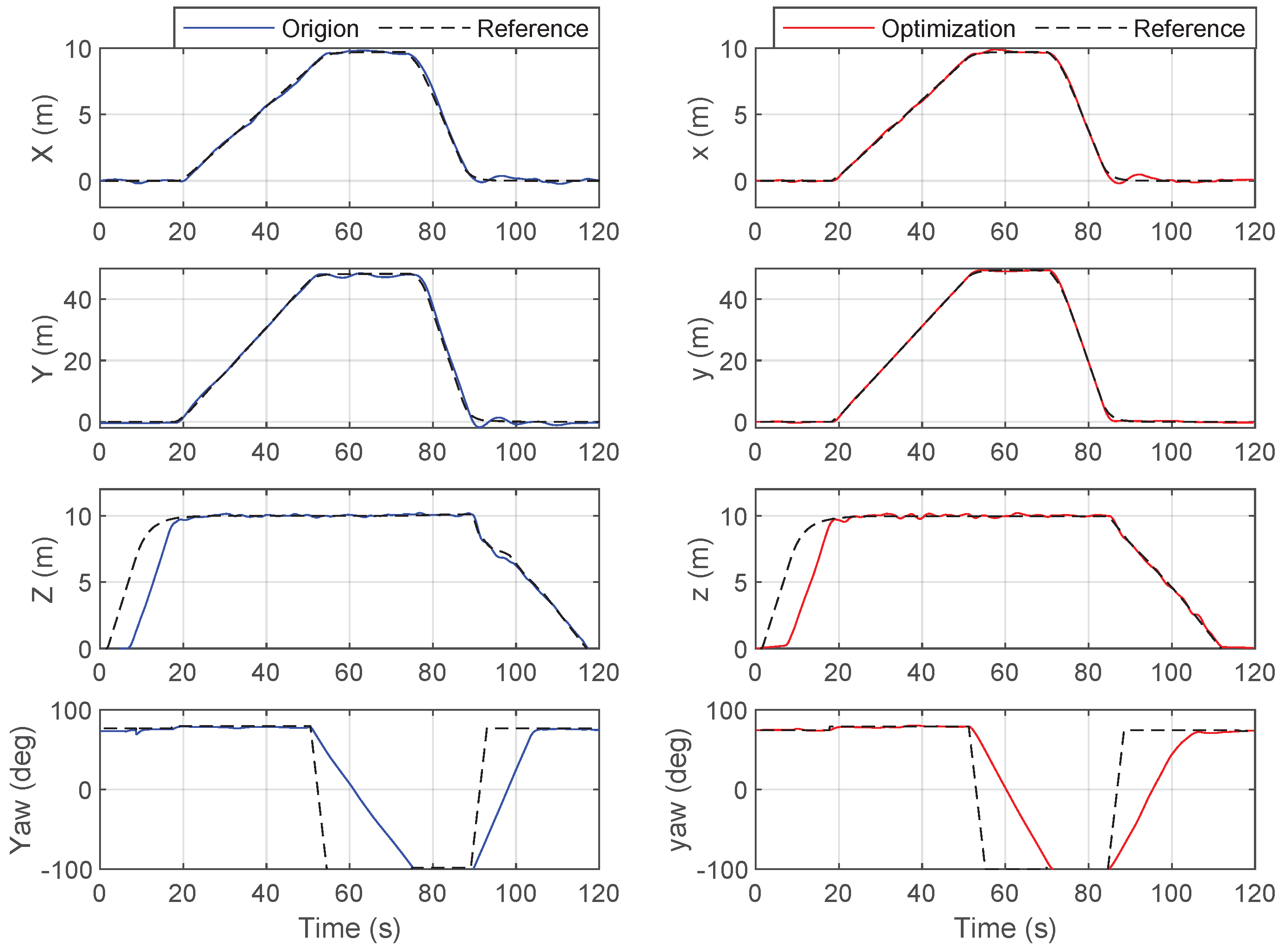
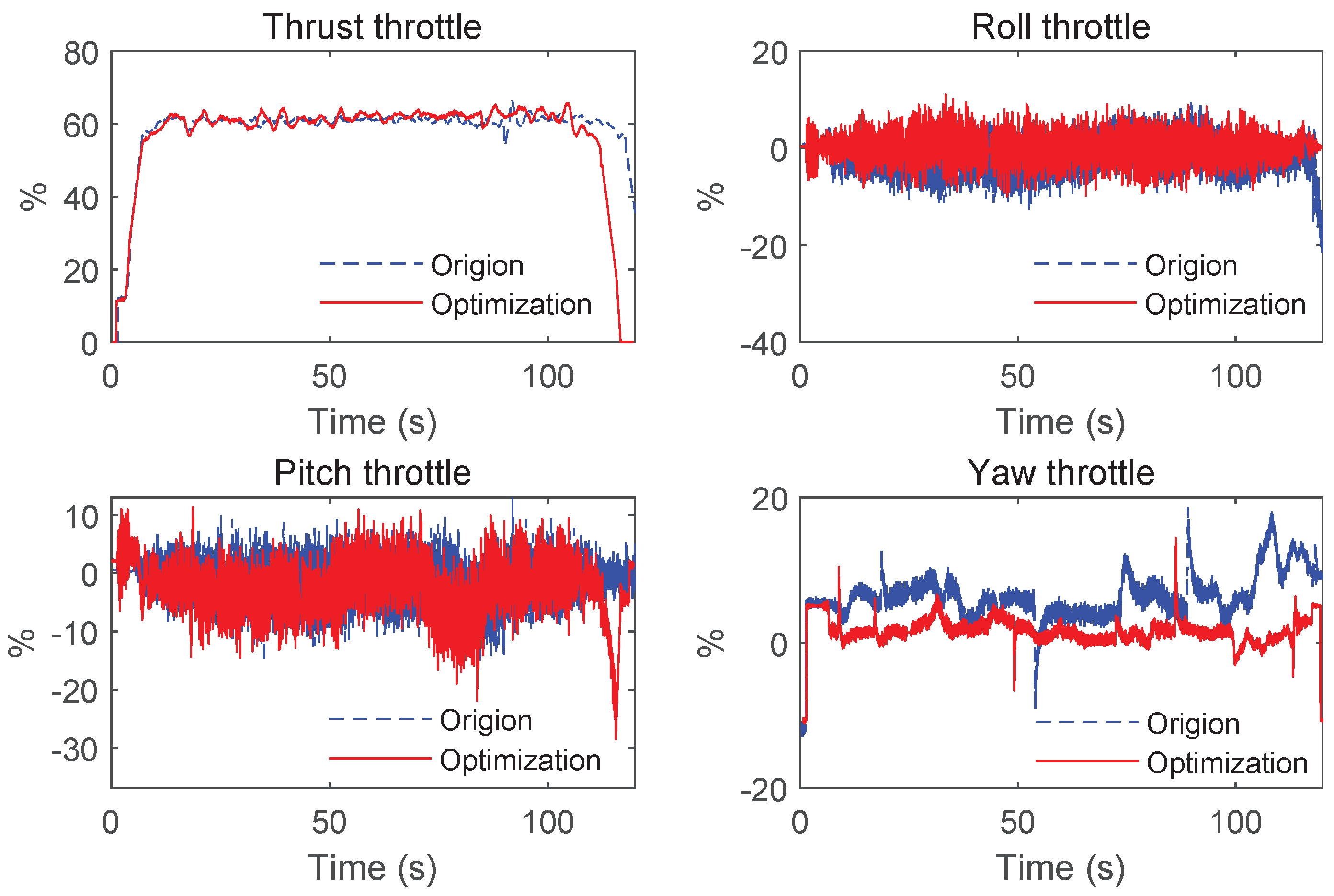
| Weight | Forward Speed | Thrust Throttle | Pitch Throttle | Pitch Angle | Power | ||||
|---|---|---|---|---|---|---|---|---|---|
| Test | Model | Test | Model | Test | Model | Test | Model | ||
| Initial Error | Load | CoG | Forward Speed | Cant Angle | Throttle Variation * | |||
|---|---|---|---|---|---|---|---|---|
| Thrust | Pitch | Roll | Yaw | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, A.; Yan, X.; Liang, W.; Zhu, S.; Chen, Z. Large-Sized Multirotor Design: Accurate Modeling with Aerodynamics and Optimization for Rotor Tilt Angle. Drones 2023, 7, 614. https://doi.org/10.3390/drones7100614
Xie A, Yan X, Liang W, Zhu S, Chen Z. Large-Sized Multirotor Design: Accurate Modeling with Aerodynamics and Optimization for Rotor Tilt Angle. Drones. 2023; 7(10):614. https://doi.org/10.3390/drones7100614
Chicago/Turabian StyleXie, Anhuan, Xufei Yan, Weisheng Liang, Shiqiang Zhu, and Zheng Chen. 2023. "Large-Sized Multirotor Design: Accurate Modeling with Aerodynamics and Optimization for Rotor Tilt Angle" Drones 7, no. 10: 614. https://doi.org/10.3390/drones7100614
APA StyleXie, A., Yan, X., Liang, W., Zhu, S., & Chen, Z. (2023). Large-Sized Multirotor Design: Accurate Modeling with Aerodynamics and Optimization for Rotor Tilt Angle. Drones, 7(10), 614. https://doi.org/10.3390/drones7100614








