Abstract
In the massive machine type of communication (mMTC), grant-free non-orthogonal multiple access (NOMA) is receiving more and more attention because it can skip the complex grant process to allocate non-orthogonal resources to serve more users. To address the limited wireless resources and substantial connection challenges, combining grant-free NOMA and multiple-input multiple-output (MIMO) is crucial to further improve the system’s capacity. In the grant-free MIMO-NOMA system, the base station should obtain the relevant information of the user before data detection. Thus, user activity detection (UAD) and channel estimation (CE) are two problems that should be solved urgently. In this paper, we fully consider the sparse characteristics of signals and the spatial correlation between multiple antennas in the grant-free MIMO-NOMA system. Then, we propose a spatial correlation block sparse Bayesian learning (SC-BSBL) algorithm to address the joint UAD and CE problems. First, by fully mining the block sparsity of signals in the grant-free MIMO-NOMA system, we model the joint UAD and CE problem as a three-dimensional block sparse signal recovery problem. Second, we derive the cost function based on the hierarchical Bayesian theory and spatial correlation. Finally, to estimate the channel and the set of active users, we optimize the cost function with fast marginal likelihood maximization. The simulation results indicate that, compared with the existing algorithms, SC-BSBL can always fully use the signal sparsity and spatial correlation to accurately complete UAD and CE under various user activation probabilities, SNRs, and the number of antennas. The normalized mean square error of CE can be reduced to 0.01, and the UAD error rate can be less than .
1. Introduction
The Internet of things (IoT) has recently become one of the most popular research directions, which allows many physical devices to be connected to the network. Massive machine type of communication (mMTC) can provide massive connections and lower latencies for devices of large-scale IoT. It plays a vital role in 5G/B5G mobile wireless communication networks. Furthermore, mMTC mainly focuses on the uplink of sporadic small-packet communication of large-scale IoT devices. That is, only a small number of devices are active and send low transmission rate short data to the access point (AP) at any time [1]. In IoT, the access point is usually a base station (BS), but with the development of unmanned aerial vehicles (UAV), it has recently been considered as a mobile base station to collect data from IoT users in remote areas [2]. Due to the excessive signaling overhead caused by the complex handshake in the scheduling process and the lack of time or frequency resources, the performance of mMTC still has some room for improvement in practical use [3].
Grant-free non-orthogonal multiple access (NOMA) has gradually become a new research direction to support the connection of large-scale devices in the IoT [4,5]. In the grant-based NOMA scheme, the BS requires predefining the transmission power or the spreading sequence of different users [6], leading to excessive signaling overheads prior to data transmission. In sporadic transmission scenarios, grant-free NOMA allows users to skip complex handshakes in the scheduling process and to transmit information directly to the BS. Thus, it could reduce complex signaling overheads and end-to-end delays [1]. In the 3GPP TSG-RAN WG1 Meeting #86, it was agreed that the grant-free NOMA scheme was suitable for mMTC [7].
In the grant-free NOMA scheme, the BS does not have a priori knowledge of each user’s activity and channel state information prior to data packet transmission. Therefore, the encapsulated pilot sequence should be used for user activity detection (UAD) and channel estimation (CE). This ensures the BS can find a small number of active users in a large potential user pool and further complete data decoding. In the downlink, the BS transmits data to the user, is always active, and does not require user activity detection. Therefore, this paper discusses UAD and CE in the uplink. Channel estimation is a widely investigated technology. Currently, many good CE schemes exist, such as [8,9], which can well estimate the information transmission channel. However, these channel estimation schemes are not perfect for all scenarios. In the grant-free NOMA scheme, a number of studies on active user detection and channel estimation have been developed wherein the NOMA detection scheme based on compressed sensing (CS) algorithm is more common. Compressed sensing can take advantage of the sparsity of signals to accurately reconstruct the original signal from a limited number of random mappings. Therefore, a CS-based algorithm can be well used in mMTC scenes with sporadic transmission characteristics. The orthogonal matching pursuit (OMP) algorithm in [10] is a classical compressed sensing algorithm, and its primary concept is to iterate between orthogonality and matching. The author in [11] compares the application effects of five multiuser detection algorithms based on the compressed sensing algorithm. A multiuser detection algorithm based on a combination of message passing (MP) and generalized approximate MP is proposed in [12], and this algorithm fully reflects the flexibility of a message-passing algorithm. However, the OMP algorithm must normalize a perceptual matrix and a priori information concerning sparsity. The MP algorithm has higher requirements for restricting the isotropy property of the perceptual matrix.
With the development of machine learning technologies, CS-based machine learning algorithms provide a new solution for solving UAD and CE problems. Among them, sparse Bayesian learning (SBL) is one of the most innovative directions in existing studies. The SBL algorithm was first systematically proposed by Michael Tipping in [13], and the SBL model was further described in [14,15]. It is based on a Bayesian hierarchical model and fully uses the potential prior information in sparse signals. Therefore, its application is convenient for describing the structure information of the signal. Simultaneously, the SBL algorithm can automatically determine the position and size of non-zero elements in the signal to be reconstructed through iteration without prior sparsity information. When the column correlation of a perceptual matrix is strong, the SBL algorithm can still maintain good performance. Block sparse Bayesian learning (BSBL) is proposed on the basis of SBL and by fully considering the block correlation in the signal. Joint UAD and CE are described as a block sparse signal recovery problem in [16], and hence a BSBL algorithm based on message passing is proposed. The authors in [17] further proposed a BSBL algorithm based on deep neural-network-assisted MP. These algorithms demonstrate that BSBL can excellently solve the UAD and CE problems in grant-free NOMA. However, most existing studies only consider a situation in which both base stations and users are equipped with a single antenna, while the situation of having multiple antennas in base stations is, relatively, less of a concern.
As a technology that has been studied for a long period of time, multiple-input multiple-output (MIMO) has now been mature. MIMO can greatly increase a system’s throughput and expand the coverage and reduce the power loss [18]. In recent years, MIMO and NOMA are often combined in a system to further improve spectral efficiency. Some studies have been conducted on UAD and CE in a MIMO-NOMA system. In [19], the author proposed two CE schemes to examine a channel’s response to frequency-selective sparse structures in the uplink of the MIMO-NOMA system. In [20], the author investigated the signal detection of large-scale grant-free MIMO-NOMA uplink systems. Based on the sparsity of user activity, they used an algorithm to detect each antenna and then fuse the obtained data on a single antenna into the final set of active users using a data fusion strategy. In [21,22], considering the joint temporal and spatial correlation, a new framework for joint UAD and CE was proposed. This framework combines the temporal correlation of active user sets with multi-antenna reception to achieve better user detection performance. However, in existing studies, some algorithms adopt relatively simple data fusion schemes, ignoring the spatial correlation of received signals between multiple antennas (e.g., [20]). Simultaneously, although some algorithms, such as [19], consider spatial correlations, the algorithms themselves are based on a conventional approach, which is inefficient and cannot converge when the number of users is large. Although the authors of [21,22] make use of spatial and temporal correlations, the time for packet transmission is very short or discrete in some practical scenarios. Therefore, the spatial correlation cannot be fully utilized.
In summary, in the grant-free MIMO-NOMA system, active users should be determined among a large number of potential users, and their channels are estimated. However, the algorithm design of joint UAD and CE involves the following challenges. First, the algorithm must address the challenge of a large number of users in mMTC networks. In this case, most conventional algorithms cannot converge quickly, and hence the effect is limited. Second, the spatial correlation between antennas should be considered in MIMO scenarios to improve the accuracy of the algorithm. Finally, the user’s channel may change rapidly. Hence, the design of the frame-by-frame CE algorithm should be considered. To address the challenges, we introduce spatial correlations in the derivation of the intelligent algorithm BSBL and make a decision based on each frame to complete the UAD and CE in the grant-free MIMO-NOMA system.
The following is the summary of the contributions of this study based on grant-free MIMO-NOMA systems:
- To fully use the sparsity and spatial correlation of the signal, we model the problem of joint user activity detection and channel estimation as the problem of the recovery of the multi-dimensional block sparse signal based on the inherent sparsity of active users in the uplink grant-free MIMO-NOMA system. Most conventional algorithms regard signal sparsity as random. Conversely, this study considers that using the block sparse structure of the signal is helpful for better active user detection.
- To address the challenge of a large number of users, we propose a spatial correlation block sparse Bayesian learning algorithm in the grant-free MIMO-NOMA system. In SC-BSBL, we can make full use of the block sparsity and spatial correlation of the signal when the user sparsity is unknown. Simulation results indicate that our algorithm can effectively improve the accuracy of joint UAD and CE in a grant-free MIMO-NOMA system.
- Currently, research on grant-free NOMA barely considers the multiple antenna scenario. The proposed SC-BSBL can make full use of the spatial correlation between signals received by different receiving antennas in a grant-free NOMA system. Thus, we improve the accuracy of joint UAD and CE in the grant-free MIMO-NOMA system and increase the richness of the algorithm in this system.
In this paper, we propose a spatial correlation block sparse Bayesian learning (SC-BSBL)-based joint user activity detection and channel estimation algorithm in the grant-free MIMO-NOMA system to solve the problems mentioned above. The algorithm is derived based on the signal block sparse model and hierarchical Bayesian theory. Therefore, it can fully use the inherent sparsity of the signals in grant-free MIMO-NOMA systems and the spatial correlation between multi-antenna-received signals to improve the accuracy of joint UAD and CE. As channel estimation is for active users, we can jointly address the UAD and CE problem. Specifically, based on the sparse characteristics and spatial correlation of the signals in the grant-free MIMO-NOMA system, first, we model the UAD and CE problem as a multi-dimensional block sparse signal recovery problem. Second, we propose a spatial correlation block sparse Bayesian learning algorithm to address this problem. In the algorithm, we derive the cost function based on the hierarchical Bayesian theory. The cost function is optimized according to the alternating minimization theory, and the estimated channel and estimated active user set are obtained. The simulation results show that the SC-BSBL algorithm can fully use the block sparsity and spatial correlation to accurately complete UAD and CE with the existence of a large number of users and unknown user sparsity in grant-free MIMO-NOMA systems.
2. System Model
2.1. Network Model
Consider a typical uplink grant-free MIMO-NOMA system, as shown in Figure 1. We assume that a large number of potential users exist in the grant-free MIMO-NOMA system. However, only a small number of users are active simultaneously, while other users are inactive. That is, the system has sporadic transmission characteristics, and active users are sparse.
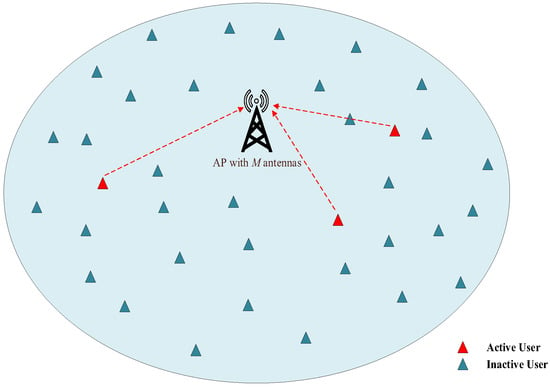
Figure 1.
An uplink grant-free MIMO-NOMA system model.
Suppose there are K users within the range of a central access point (e.g., UAV or base station). When the user needs to transfer data, it is in the active state, and the probability that the user is in the active state is . The number of sub-carriers of the system is N. Assume that all users are equipped with a single antenna and the access point is equipped with M antennas. To meet the requirements of massive connections in the IoT, we consider the overload system (i.e., ). Additionally, we consider the low-density signature OFDM (LDS-OFDM) [23] communication system in the code field NOMA, and the QPSK modulation mode is used in this system.
2.2. Signal Sparse Model
We develop a sparse signal model by fully using the sparse characteristics of active users in the grant-free MIMO-NOMA system. For each active user, its binary information sequence is encoded with length , whereas the information sequence is 0 for inactive users. To complete the channel estimation, we assign each user a unique training sequence. The length of the training sequence is , and information sequence is the length of . It should be noted that the length of the training sequence cannot be excessively long, so the sequence cannot be orthogonal. In this study, we use the Zadoff–Chu sequence with good auto-correlation and cross-correlation as the training sequence [24]. Subsequently, each symbol in is mapped to D subcarriers with a low-density spreading sequence, , which is a sparse vector of length N and contains D non-zero elements. In this manner, the same sequence, , is transmitted on D, which is a different subcarrier.
In the grant-free MIMO-NOMA system, users have sporadic transmission characteristics, that is, only a small number of users are active at the same time. Therefore, we define as the active user indicator for user k. When the user is active, takes a value of 1. Otherwise, takes a value of 0. We incorporate into the signal matrix: .
Thereafter, the signal of the n-th carrier received by the access point on the m-th antenna can be expressed as follows:
where is user k’s components of the spread spectrum sequences on the n-th carrier received by the m-th antenna, and is the channel coefficient of user k on the n-th carrier received by the m-th antenna, which is assumed to be independently and identically distributed (i.i.d) with a zero mean complex Gaussian distribution. When the UAV is used as the access point, we assume that the distance between the UAV and the user is constant in a time slot. Further, is the component of the noise vector and follows complex Gaussian distribution .
At the matrix level, the signal received by the m-th antenna at the AP can be expressed as follows:
where the -th entry of , -th entry of , and -th entry of represent the l-th received symbol on the n-th subcarrier, l-th transmitted symbol of the k-th user, and , respectively. Further, is the noise matrix.
Then, the signal received by the M antennas at the access point can be expressed as follows:
Due to the sparse user activity, channel matrix is row sparse. That is, has the property of being block sparse (Figure 2). As described in (3), is a three-dimensional matrix of size . When information on the subcarrier exists, this indicates that the channel vector corresponds to the active user; otherwise, it is the channel of the inactive user. Therefore, is sparse in the user dimension. In the carrier dimension, the user’s information is mapped to D subcarriers. As the low-density sequence is sparse, the carrier dimension is also sparse. The information transmitted by user k on the same subcarrier n has spatial correlations on different antennas, m, and this correlation can be fully utilized.
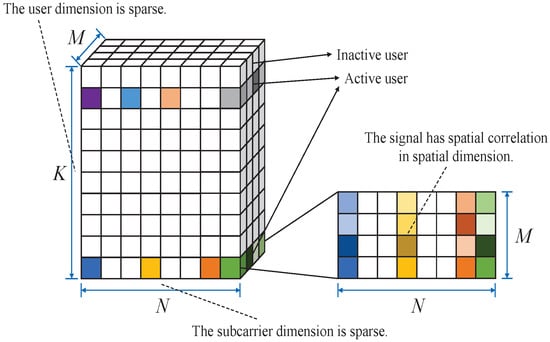
Figure 2.
Schematic diagram of the elements in channel matrix .
3. SC-BSBL Algorithm in Grant-Free MIMO-NOMA
Based on the sparse signal model, we propose the spatial correlation block sparse Bayesian learning algorithm to complete the joint UAD and CE in grant-free MIMO-NOMA systems. First, based on the expressions of the channel and received signal models, we derive the posterior probability density of the channel and the likelihood function of the received signal. Moreover, we represent the likelihood function as the form of the cost function. Finally, the cost function is optimized by alternating minimization, and hence the final estimated channel and the estimated active user set are obtained.
3.1. Problem Formulation
In a grant-free MIMO-NOMA system, as the active status and channel information of users is not prior knowledge, relevant information should be obtained from the received signal. According to the combination of , can be decomposed into , where and represent the signal matrix of the received training sequence and data sequence, respectively. Further, can be expressed as follows:
In the LDS-OFDM system, the transmission sequence of each user is mapped to D subcarriers, and the access point knows the location of all non-zero elements. Therefore, we can eliminate the zero elements in each user’s channel matrix to simplify channel matrix . (4) can be further expressed as follows:
After decomposing and removing the zero elements, the proposed SC-BSBL algorithm is used to further process for user active detection and channel estimation. Therefore, (5) is the formula of the problem to be solved. Assuming that the training sequence is known at AP, this problem is equivalent to a recovery problem that involves the multi-dimensional block sparse signal. In block-sparse Bayesian theories, the most basic mathematical model is expressed as follows:
where is the observation matrix, is the underdetermined perceptual matrix, is the block sparse signal matrix that needs to be recovered, and is the observation noise.
The block sparse Bayesian theory aims to solve underdetermined matrix . However, when satisfies the restricted isotropy property (RIP), block sparse signal can be accurately reconstructed from observation matrix [25,26].
According to block sparse Bayesian learning theory and proposed signal sparse model, in (5) can be considered known perception matrix in (6), in (5) can be regarded observation matrix in (6), and is the matrix to be reconstructed. Therefore, the joint user active detection and channel estimation problem in the grant-free MIMO-NOMA system is transformed into the problem of multi-dimensional block sparse signal recovery.
3.2. Representation of the Cost Function for Joint UAD and CE
As described in the previous section, is a block sparse matrix. On the m-th antenna, the i-th channel, , obeys a complex Gaussian distribution:
where , . To fully use the spatial correlation, we regard multiple channels between different antennas and the k-th user as an entire block. Specifically, represents the correlation between the entire block of channel matrix and received signal matrix . For larger , will be the channel of the active user, and for smaller , will be noise. Further, is the covariance matrix of . The positive definite matrix, , represents the correlation structure information in channel .
According to the matrix Gaussian probability density expression, the channel model is equivalent to the following:
For received signal at the m-th antenna, it conforms to the following expression:
where the noise in (4) obeys complex Gaussian distribution . As described in the previous chapter, can be considered the known perception matrix, , in (6). In order to facilitate the expression, we define .
Using the channel and the received signal models, posterior probability density and likelihood function are further expressed as:
with
To make full use of the spatial correlation between the received signals on different receiving antennas, we combine the received signals on all antennas into a three-dimensional matrix. Then, the likelihood function of M antennas is expressed as follows:
By utilizing the type-II maximum likelihood estimation method, the cost function can be expressed as follows:
3.3. Optimization of the Cost Function for Joint UAD and CE
For the optimization of the cost function (16), we can calculate the partial derivative of parameter , , and , and obtain the updated formula of the corresponding parameters. In the optimization process, we regard the i-th channel on the M antennas as an entire block signal to utilize the spatial correlation. Hyperparameter represents the correlation of the entire block signal.
By calculating the partial derivative of parameter in (16), we can obtain the following:
By solving , we can obtain the updated formula of .
Parameters and can be optimized simultaneously using the fast marginal likelihood maximization (FMLM) method. In practical applications, is mostly set to a constant. We set the value of as . To facilitate the expression, we define the following:
We can decompose in (19) into the following:
where subscripts i and j represent the i-th and j-th basis vectors in the matrix, respectively. With , it represents the remaining part after removing the base i-th vector from .
can be further expressed as:
with
where and . is a sparse factor, which represents the degree of overlap between the basis vector and existing vectors in the model. Moreover, is the quality factor, which refers to the alignment measure without the model error of vector [15].
In (21), is a function independent of , while is only related to . Suppose that, when is optimized, the rest of the basis vectors in the model remain constant. By calculating the partial derivative of in (23), we can obtain the following:
By solving , we can obtain the updated formula of .
In (25) and (18), to improve the accuracy of the joint UAD and CE, we regard the received signals on all antennas, in general, to fully use the spatial correlation between the algorithm.
Algorithm 1 is the proposed SC-BSBL algorithm. In this algorithm, we can use alternating minimization to optimize the cost function (16). First, assuming that is known, we optimize to obtain the updated value of . Second, the updated is used to calculate . Finally, is updated according to (18). In this manner, alternate updates are performed to optimize the cost function.
| Algorithm 1 SC-BSBL algorithm for joint UAD and CE in grant-free MIMO-NOMA |
Input: received signal , training matrix Output: estimated channel , estimated set of active users |
In the iterative process, steps 5 and 6 aim to find a basis vector that maximizes the change in in all to update to improve the efficiency of the algorithm. In the algorithm, and represent the basis vector to be updated, and the change observed in , respectively. For the update of the parameters in step 7, adding, deleting, or re-estimating a block is possible, and the detailed process of parameter updates can utilize the method proposed in [15].
When the normalized variation between the two iterations is less than the set exit condition, the iteration is stopped. According to the known position of the zero element at the access point, insert the zero element into the corresponding position of . The final value of the is estimated channel . As discussed previously in this section, indicates the correlation of the i-th channel. When is greater than the threshold , the user can be considered active. Consequently, we can obtain the active user set .
3.4. Algorithm Complexity
The complexity of the proposed SC-BSBL algorithm is mainly caused by matrix inversions and the accumulation operation. Specifically, the algorithm has the complexity of , , , and in steps 4, 7, 8, and 9, respectively. Therefore, the complexity of each iteration of the SC-BSBL algorithm is . In the grant-free MIMO-NOMA system, the values of D and are small relative to the number of subcarriers N and the length of the signal sequence , so the high-order term in the complexity of the algorithm is acceptable.
The computational complexity of the BSBL algorithm that is performed independently for the received signal on each antenna is . Unlike the independent detection algorithm, the SC-BSBL algorithm reduces the computational complexity of joint UAD and CE. Simultaneously, by fully using the spatial correlation of the signals received by each antenna, we also improve the accuracy of the joint UAD and CE in the grant-free MIMO-NOMA system.
4. Simulation Results
In this section, the simulation considers the active user detection scenario in the frame-based uplink grant-free MIMO-NOMA system to verify the effectiveness of the SC-BSBL algorithm. Table 1 presents the relevant simulation parameters. The channel is set to the block fading channel, and its elements obey the independent complex Gaussian distribution . The number of potential users in the grant-free MIMO-NOMA system is often large, we set its default value to 300. Additionally, we set the threshold to 0.1 based on the experience of existing research.

Table 1.
Related simulation parameters.
To verify the accuracy of channel estimation, we use normalized mean square error (NMSE) and NMSE as performance parameters in the simulation. Specifically, NMSE represents an error between the estimated channel and the original channel. The smaller NMSE, the higher the accuracy of the channel estimations. NMSE denotes an error between the signal calculated by the estimated channel and the primitive signal. It can judge the accuracy of channel estimation from signal recovery. By definition, NMSE and NMSE can be expressed as follows:
Meanwhile, we evaluate the performance of user activity detection by UAD error rate, probability of missed detection , and probability of false alarm . If the user has the condition of missing detection or a false alarm, it is considered a detection failure. UAD error rate is the ratio of all failed detection users to total active users and it represents the overall accuracy of UAD. and provides the performance of UAD in more detail.
Inspired by [27,28], to verify the feasibility of the algorithm in dynamic scenarios, we provide the simulation results in that scenario. We also simulate the influence of a different number of antennas M on the performance of the algorithm. In the rest of the simulation, we set the number of antennas to eight, which is commonly adopted in practice.
We also provided the performance of the following four algorithms for comparison:
- Orthogonal matching pursuit (OMP) [10]: This algorithm is a conventional CS algorithm, which requires a priori knowledge of the sparsity of the signal to be reconstructed.
- Generalized approximate message passing (GAMP) [29]: This algorithm is a derivative of the iterative threshold reconstruction algorithm, which reduces the complexity of the message-passing algorithm by approximating the conventional message-passing algorithm.
- MIMO-NOMA-DL: In MIMO-NOMA-DL, we extend the model of [30] to multiple antennas to complete UAD and CE in multi-antenna scenarios.
- Random sparsity learning multiuser detection (RSL-MUD) [31]: The algorithm regards CE and UAD as a dictionary learning problem and solves the problem based on bilinear generalized approximate message passing.
4.1. Convergence of SC-BSBL
Figure 3 shows the convergence of the SC-BSBL algorithm under different SNRs and antenna numbers M. We simulate the convergence of SC-BSBL when M = 2 and M = 8 and SNR = −5 dB, SNR = 5 dB, and SNR = 15 dB. In the simulation, we set the number of active users to 30 to ensure fairness.
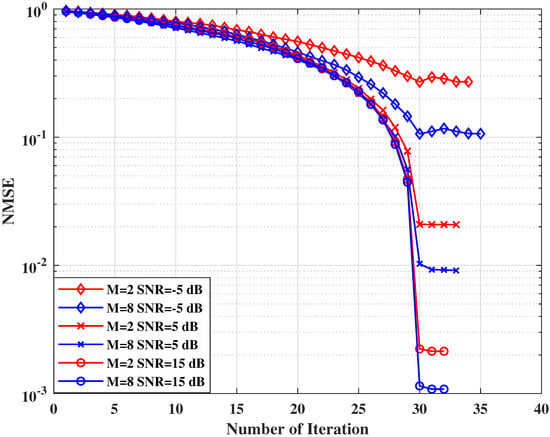
Figure 3.
Convergence of the SC-BSBL.
In the SC-BSBL, we start with ; that is, at the beginning of the algorithm, all basis vectors are not in the model. After obtaining all the for updates, we choose a base that maximizes the change in for the operation to achieve rapid declines. As the SC-BSBL updates, only one base at a time maximizes the change in , and the NMSE reduction per iteration is similar. Therefore, the iterative convergence curve shows the trend in Figure 3. As observed in Figure 3, when the number of iterations equals the number of active users, the algorithm tends to converge because only one base is updated per iteration and all active users have been found after updating 30 bases. After 30 iterations, the algorithm performs block re-estimations to further make the estimated channel close to the original channel. In the case of a low SNR, the SC-BSBL may misestimate the active users, leading to an increase in the NMSE. The algorithm misestimates one user while M = 2 and SNR = −5 dB. When M = 8 and SNR = −5 dB, the algorithm misestimates two users. Noted that the occurrence of wrong users is random and is not related to the number of antennas. When M = 8, SC-BSBL can make full use of spatial correlations so that the performance of the channel’s estimation is better than that of M = 2.
4.2. Performance of Channel Estimation
Figure 4 shows the NMSE of the algorithms under different activation probabilities . Here, represents the probability that each user may be activated, and the definition of NMSE is shown in (26). In the simulation, we set the number of antennas to eight, which is a common setting in algorithm simulations. We set the SNR to 5 dB, and to demonstrate the performance of the SC-BSBL algorithm in different SNR situations, we simulated channel estimations when SNR = 15 dB. We also simulate the channel estimation performance of the proposed algorithm in a dynamic scene channel model.
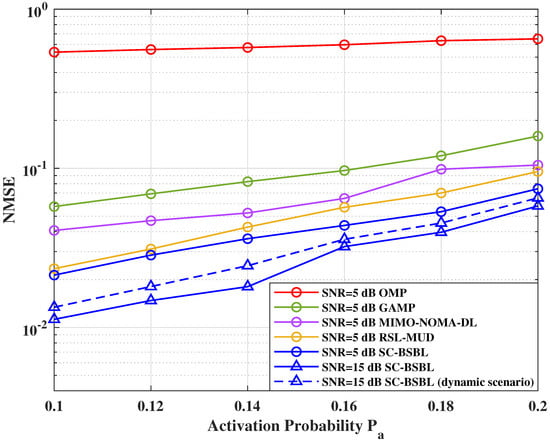
Figure 4.
NMSE performance under different activation probabilities .
As can be seen from Figure 4, with an increase in the activation probability, the NMSE of each algorithm gradually worsens. The algorithms used in this simulation are all based on the characteristics of sparse data. However, an increase in potential users in the system leads to a decrease in sparsity. Thus, the NMSE of the algorithm worsens. The proposed SC-BSBL algorithm fully considered the block sparse property of the system and the spatial correlation between antennas in the model’s derivation. Therefore, a high NMSE level can still be maintained when the sparsity is low. The NMSE of the OMP algorithm is poor and changes little with changes in . Meanwhile, the changing trend of GAMP, RSL-MUD, and MIMO-NOMA-DL algorithms is more evident. In the simulation, we set the prior sparsity of the OMP algorithm to a fixed value. Therefore, the NMSE curve of the algorithm hardly changes with the change in the activation probability. In Figure 4, the NMSE of the SC-BSBL algorithm is better than other algorithms under different activation probabilities. Moreover, it can still meet the system’s requirements when the activation probability is 0.2, whereas the other algorithms have poor performance. In addition, the SC-BSBL algorithm remains applicable to dynamic scenarios. We simulate the performance of the proposed algorithm under the UAV channel used in [32]. For the uplink transmission from an IoT user to the UAV, the channel gain is composed of line-of-sight and non-line-of-sight components, which vary with the distance between the UAV and the IoT user. Affected by the change of the channel with distance in the UAV-assisted ground communication network, the channel estimation performance of the SC-BSBL algorithm is degraded, but can still meet the basic performance requirements.
As shown in Figure 5, when the user activation probability and SNR are the same, the NMSE of channel estimation increases with an increase in the number of potential users. This is because, when the number of subcarriers in the system is constant, the number of potential users decreases, and the overload rate of the system also decreases. Moreover, SC-BSBL is an additive search algorithm. When active users are few, the algorithm can converge faster and have better estimation results. Meanwhile, the relationship between the comparison algorithms in Figure 5 is the same as that in Figure 4. Therefore, the change in the number of potential users only affects the channel estimation performance of each algorithm.
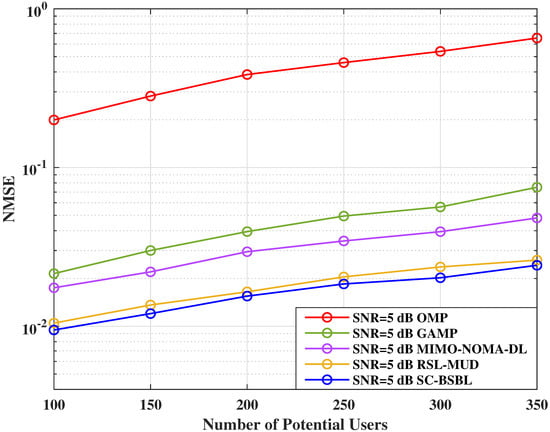
Figure 5.
NMSE performance under different numbers of potential users K.
Figure 6 shows the NMSE of the algorithms under different activation probabilities. In the OMP, GAMP, and SC-BSBL algorithms, we substitute the estimated channel, , into (3). The estimated noise, , can be solved, and then, the estimated signal can be obtained.
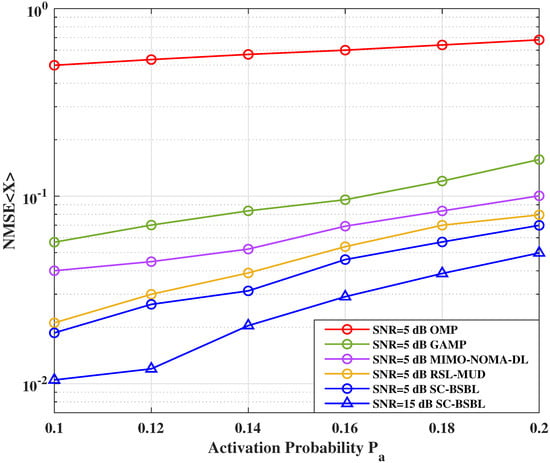
Figure 6.
NMSE performance under different activation probabilities .
As shown in Figure 6, the channel estimated by the SC-BSBL algorithm achieves good performance for signal recovery. In the simulation, the signal recovery performance of OMP, GAMP, and SC-BSBL algorithms depends on the accuracy of channel estimation. The RSL-MUD algorithm provides the function of recovering the signal while estimating the channel, and the performance of the two is similar. We trained the model of the MIMO-NOMA-DL algorithm for signal recovery. We found that the performance of the algorithm for signal recovery is also the same as that for channel estimation. As we use the NMSE to judge the signal recovery capability and channel estimation capability, the overall trend and position relationship of Figure 4 and Figure 6 are similar. Nevertheless, we can still learn from Figure 6 that the proposed SC-BSBL algorithm has advantages in signal recovery.
4.3. Performance of User Activity Detection
Figure 7 shows the UAD error rate of the algorithm under different SNRs. The UAD error rate is an overall index that can test the UAD ability of the algorithm. To discuss the performance of UAD in more detail, Figure 8 and Figure 9 provide the probability of missed detection and probability of false alarm under different activation probabilities .
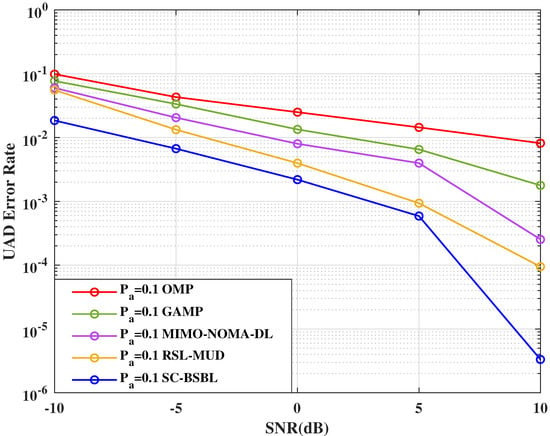
Figure 7.
UAD error rate under different SNRs.
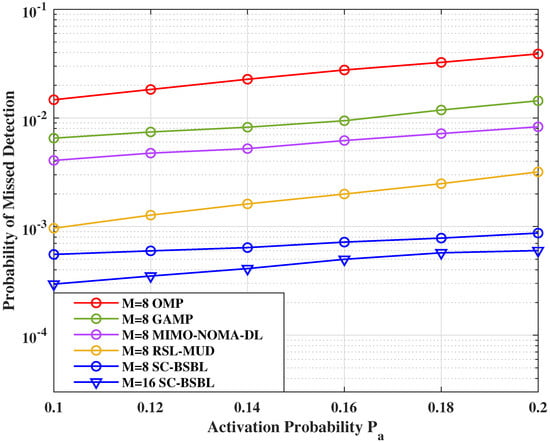
Figure 8.
Probability of missed detection under different activation probabilities .
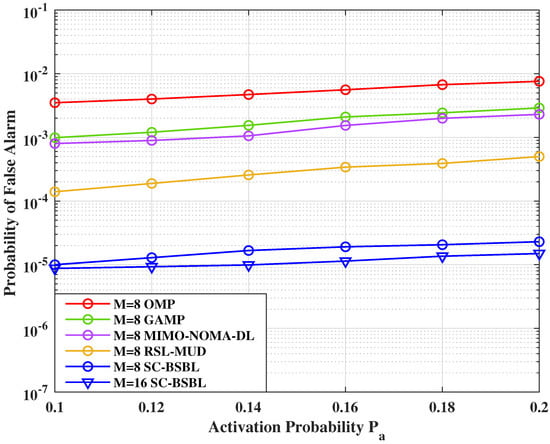
Figure 9.
Probability of false alarm under different activation probabilities .
As shown in Figure 7, the UAD error rate of the algorithms decreases with an increase in SNR. When the SNR is low, the UAD performance of OMP, GAMP, and MIMO-NOMA-DL algorithms is very poor, while that of the SC-BSBL algorithm is clearly better. When SNR > 5 dB, almost no error occurs in the active user detection of the SC-BSBL algorithm. Noted that the active user detection performance of the SC-BSBL algorithm is better than its channel estimation performance in a low-SNR scenario. We can simply understand that the corresponding channel is activated only when the user is active. Therefore, the performance of active user detection is related to the performance of channel estimations. However, the channel estimation performance of the OMP algorithm is worse than that of other algorithms. Hence, its active user detection performance is also poor. Specifically, the proposed SC-BSBL algorithm is based on the block sparse Bayesian principle, which detects active users by finding non-zero blocks in sparse data. Therefore, compared with other algorithms, the SC-BSBL algorithm can always find active users well when SNRs are poor. When the sparsity is high and the interference is lower, the SC-BSBL algorithm has a very strong ability to find active users, and almost no active user detection errors occur.
As can be seen from Figure 8 and Figure 9, similar to channel estimation, the performance of UAD decreases with the decrease of sparsity. However, noted that benefit from the experience-based threshold selection, the UAD performance of the proposed algorithm is less affected by sparsity than other algorithms. We also simulate and with a different number of antennas. As expected, the increase in the number of antennas will improve the performance of UAD as more observation information can be obtained by BS. Compared with Figure 8, the performance of the proposed algorithm is significantly lower than that of other algorithms in Figure 9. This is because the SC-BSBL algorithm is constructive and the probability of a false alarm will be reduced.
4.4. Influence of the Number of Antennas
Figure 10 shows the variation curve of the NMSE under different antenna numbers. In the simulation, we set to 0.1 and SNR to 5 dB. To demonstrate the channel estimation performance of SC-BSBL under different antennas in scenes with higher SNR, we also simulate it when SNR = 15 dB.
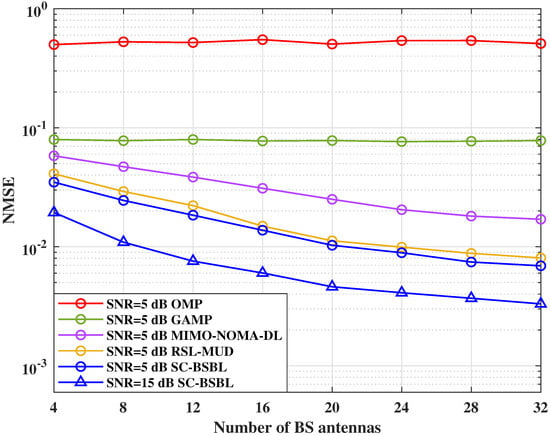
Figure 10.
NMSE under different numbers of BS antennas M.
From Figure 10, we can see that the NMSE of the MIMO-NOMA-DL, RSL-MUD, and the proposed SC-BSBL algorithm improves with an increase in the number of antennas, M. However, the NMSE of the OMP and GAMP algorithms does not change with an increase in the number of antennas. When = 0.1 and SNR = 15 dB, the proposed SC-BSBL algorithm achieves good performance in the case of the various antennas. Both OMP and GAMP algorithms process the signals received by each antenna separately, and then they fuse all processing results. Therefore, the change in the number of antennas will not affect the performance of their channel estimation. Neither of these two algorithms fully considers the spatial correlation between the signals received by each antenna. Particularly, the MIMO-NOMA-DL algorithm regards the signals received on all antennas in general. Thus, its channel estimation performance improves with an increase in the number of antennas. However, due to the problems of deep learning itself, the performance of the MIMO-NOMA-DL algorithm is slightly worse than that of the SC-BSBL algorithm under the same conditions. The RSL-MUD algorithm considers the structure of a multi-layer message-passing factor graph. Therefore, spatial correlations can be used to improve the reconstruction performance of multi-dimensional sparse signals. The proposed SC-BSBL algorithm makes full use of the spatial correlation between the received signals of each antenna. Thus, the performance improves with an increase in the number of antennas; then, the simulation results are also consistent with BSBL’s theory.
4.5. Algorithm Comparison
We also provided the performance of four algorithms in the simulation for comparison. The simulation results indicate that the OMP algorithm, as a conventional CS algorithm that needs to know the sparsity in advance, has the worst reconstruction performance. The GAMP algorithm reconstructs sparse signals by using a message-passing factor graph, so it can complete the channel estimation without specifying the sparsity, and its recovery performance is better than that of the OMP algorithm. However, both OMP and GAMP algorithms fail to fully use the spatial correlation between the receiving antennas. Therefore, their channel estimation performance is limited in MIMO systems. Compared with these two algorithms, the MIMO-NOMA-DL and RSL-MUD algorithms can make use of spatial correlation. As the MIMO-NOMA-DL algorithm is model-driven, the performance of the MIMO-NOMA-DL algorithm degrades when the same model is used in different activation probabilities. However, as the SC-BSBL algorithm is iterated independently for each case, it can maintain a high level of performance under various conditions. Meanwhile, the channel estimation performance of the RSL-MUD algorithm is worse than that of the SC-BSBL algorithm because of the high requirement of the finite isometry of a perceptual matrix. Overall, compared with other algorithms, the proposed SC-BSBL algorithm can fully use the signal sparsity and spatial correlation to accurately complete user active detection and channel estimation.
5. Conclusions
In this paper, we proposed a spatial BSBL algorithm to solve the joint UAD and CE problems in grant-free MIMO-NOMA systems. The block sparsity of signals and the spatial correlation between antennas were fully used. First, by fully mining the block sparsity of signals in the grant-free MIMO-NOMA system, the channel estimation problem was modeled as a three-dimensional block sparse signal recovery problem. Second, we derived the cost function to solve the problem based on the hierarchical Bayesian theory and optimize it with fast marginal likelihood maximization to obtain the estimated channel and set of estimated active users. The simulation results indicate that the proposed SC-BSBL algorithm can always make use of the sparse characteristics and spatial correlation of signals to accurately complete the combination of UAD and CE when no prior information exists, and a large number of users are available in the grant-free MIMO-NOMA system. This study restricts general grant-free MIMO-NOMA scenarios; the simulation results indicate that the proposed algorithm can be used in mobile scenes, but its reconstruction performance degrades. Additionally, the current cost function optimization uses the FMLM method, which has a poor convergence effect when the number of users is large, or the SNR is low. For future work, we will investigate a novel user activity detection and channel estimation algorithm in the UAV-assisted ground communication network to have better detection performance when the channel varies with the position of the UAV. Moreover, we will consider using a more intelligent cost function optimization method to expand the application range of the algorithm.
Author Contributions
All the authors contributed equally to the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grant 61901043; the Qin Xin Talents Cultivation Program, Beijing Information Science and Technology University under Grant QXTCP B202101; and the R&D Program of Beijing Municipal Education Commission (KM202211232010).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shahab, M.B.; Abbas, R.; Shirvanimoghaddam, M.; Johnson, S.J. Grant-Free Non-Orthogonal Multiple Access for IoT: A Survey. IEEE Commun. Surv. Tutor. 2020, 22, 1805–1838. [Google Scholar] [CrossRef]
- Dai, H.; Zhang, H.; Li, C.; Wang, B. Efficient deployment of multiple UAVs for iot communication in dynamic environment. China Commun. 2020, 17, 89–103. [Google Scholar] [CrossRef]
- Bockelmann, C.; Pratas, N.; Nikopour, H.; Au, K.; Svensson, T.; Stefanovic, C.; Popovski, P.; Dekorsy, A. Massive machine-type communications in 5G: Physical and MAC-layer solutions. IEEE Commun. Mag. 2016, 54, 59–65. [Google Scholar] [CrossRef]
- Liu, H.; Li, G.; Li, X.; Liu, Y.; Huang, G.; Ding, Z. Effective Capacity Analysis of STAR-RIS-Assisted NOMA Networks. IEEE Wirel. Commun. Lett. 2022, 11, 1930–1934. [Google Scholar] [CrossRef]
- Li, X.; Zheng, Y.; Zeng, M.; Liu, Y.; Dobre, O.A. Enhancing Secrecy Performance for STAR-RIS NOMA Networks. IEEE Trans. Veh. Technol. 2022, 1–6. [Google Scholar] [CrossRef]
- Zhang, Y.; He, W.; Li, X.; Peng, H.; Rabie, K.; Nauryzbayev, G.; ElHalawany, B.M.; Zhu, M. Covert Communication in Downlink NOMA Systems With Channel Uncertainty. IEEE Sens. J. 2022, 22, 19101–19112. [Google Scholar] [CrossRef]
- Huawei; HiSilicon. Discussion on Grant-Free Transmission; Technical Report document R1-166095, TSG-RAN WG1 Meeting #86, 3GPP; Sophia Antipolis: Provence, France, 2016. [Google Scholar]
- Liu, C.; Liu, X.; Ng, D.W.K.; Yuan, J. Deep Residual Learning for Channel Estimation in Intelligent Reflecting Surface-Assisted Multi-User Communications. IEEE Trans. Wirel. Commun. 2022, 21, 898–912. [Google Scholar] [CrossRef]
- Gu, X.; Chen, Y. Channel-Estimation-Aware Joint Radar-Communications Designs. In Proceedings of the 2022 IEEE 95th Vehicular Technology Conference: (VTC2022-Spring), Helsinki, Finland, 19–22 June 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Shim, B.; Song, B. Multiuser Detection via Compressive Sensing. IEEE Commun. Lett. 2012, 16, 972–974. [Google Scholar] [CrossRef]
- Oyerinde, O.O. Compressive Sensing Algorithms for Multiuser Detection in Uplink Grant Free NOMA Systems. In Proceedings of the 2019 IEEE 89th Vehicular Technology Conference (VTC2019-Spring), Kuala Lumpur, Malaysia, 28 April–1 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Gao, Y.; Zheng, J.; Li, B. Multiuser Detection of GF-NOMA with Dynamic-Active Users and Temporal-Correlated Channels. IEEE Commun. Lett. 2022, 26, 2380–2384. [Google Scholar] [CrossRef]
- Tipping, M.E. Sparse Bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Tipping, M.E. Bayesian inference: An introduction to principles and practice in machine learning. In Proceedings of the Summer School on Machine Learning; Springer: Berlin/Heidelberg, Germany, 2003; pp. 41–62. [Google Scholar]
- Tipping, M.E.; Faul, A.C. Fast marginal likelihood maximisation for sparse Bayesian models. In Proceedings of the Ninth International Workshop on Artificial Intelligence and Statistics, Key West, FL, USA, 3–6 January 2003; PMLR: New York, NY, USA, 2003; pp. 276–283. [Google Scholar]
- Zhang, Y.; Guo, Q.; Wang, Z.; Xi, J.; Wu, N. Block Sparse Bayesian Learning Based Joint User Activity Detection and Channel Estimation for Grant-Free NOMA Systems. IEEE Trans. Veh. Technol. 2018, 67, 9631–9640. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Y.; Huang, C.; Guo, Q.; Yuen, C.; Guan, Y.L. DNN-Aided Block Sparse Bayesian Learning for User Activity Detection and Channel Estimation in Grant-Free Non-Orthogonal Random Access. IEEE Trans. Veh. Technol. 2019, 68, 12000–12012. [Google Scholar] [CrossRef]
- Chen, Z.; Sohrabi, F.; Yu, W. Multi-Cell Sparse Activity Detection for Massive Random Access: Massive MIMO Versus Cooperative MIMO. IEEE Trans. Wirel. Commun. 2019, 18, 4060–4074. [Google Scholar] [CrossRef]
- Haq, I.U.; Nawaz, S.J.; Mansoor, B.; Baltzis, K.B. Superimposed Pilots based Estimation of Sparse Multipath massive-MIMO NOMA Channels. In Proceedings of the 2019 8th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 13–15 May 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Tan, S. Research on Signal Detection Method based on Quantum Bacterial Foraging Optimization in Massive MIMO NOMA Systems. Ph.D. Thesis, Nanjing University of Posts and Telecommunications, Nanjing, China, 2020. [Google Scholar]
- Wu, L.; Sun, P.; Wang, Z.; Yang, Y. Joint User Activity Identification and Channel Estimation for Grant-Free NOMA: A Spatial-Temporal Structure-Enhanced Approach. IEEE Internet Things J. 2021, 8, 12339–12349. [Google Scholar] [CrossRef]
- Wu, L.; Wang, Z.; Sun, P.; Yang, Y. Temporal Correlation Enhanced Sparse Activity Detection in MIMO Enabled Grant-Free NOMA. IEEE Trans. Veh. Technol. 2022, 71, 2887–2899. [Google Scholar] [CrossRef]
- Razavi, R.; AL-Imari, M.; Imran, M.A.; Hoshyar, R.; Chen, D. On Receiver Design for Uplink Low Density Signature OFDM (LDS-OFDM). IEEE Trans. Commun. 2012, 60, 3499–3508. [Google Scholar] [CrossRef]
- Chu, D. Polyphase codes with good periodic correlation properties (Corresp.). IEEE Trans. Inf. Theory 1972, 18, 531–532. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B. An Introduction to Compressive Sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Liu, B.; Fan, H.; Lu, Z.; Fu, Q. Scan-based Compressed Terahertz Imaging and Real-Time Reconstruction via the Complex-valued Fast Block Sparse Bayesian Learning Algorithm. arXiv 2013, arXiv:1309.6195. [Google Scholar]
- Liu, C.; Yuan, W.; Li, S.; Liu, X.; Li, H.; Ng, D.W.K.; Li, Y. Learning-Based Predictive Beamforming for Integrated Sensing and Communication in Vehicular Networks. IEEE J. Sel. Areas Commun. 2022, 40, 2317–2334. [Google Scholar] [CrossRef]
- Cheng, X.; Duan, D.; Gao, S.; Yang, L. Integrated Sensing and Communications (ISAC) for Vehicular Communication Networks (VCN). IEEE Internet Things J. 2022, 9, 23441–23451. [Google Scholar] [CrossRef]
- Li, B.; Zheng, J.; Gao, Y. Compressed Sensing Based Multiuser Detection of Grant-Free NOMA with Dynamic User Activity. IEEE Commun. Lett. 2022, 26, 143–147. [Google Scholar] [CrossRef]
- Kim, W.; Ahn, Y.; Shim, B. Deep Neural Network-Based Active User Detection for Grant-Free NOMA Systems. IEEE Trans. Commun. 2020, 68, 2143–2155. [Google Scholar] [CrossRef]
- Ding, T.; Yuan, X.; Liew, S.C. Sparsity Learning-Based Multiuser Detection in Grant-Free Massive-Device Multiple Access. IEEE Trans. Wirel. Commun. 2019, 18, 3569–3582. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, L.; Liang, Y.C. Deep Reinforcement Learning for Channel and Power Allocation in UAV-enabled IoT Systems. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).