Respiration Detection of Ground Injured Human Target Using UWB Radar Mounted on a Hovering UAV
Abstract
:1. Introduction
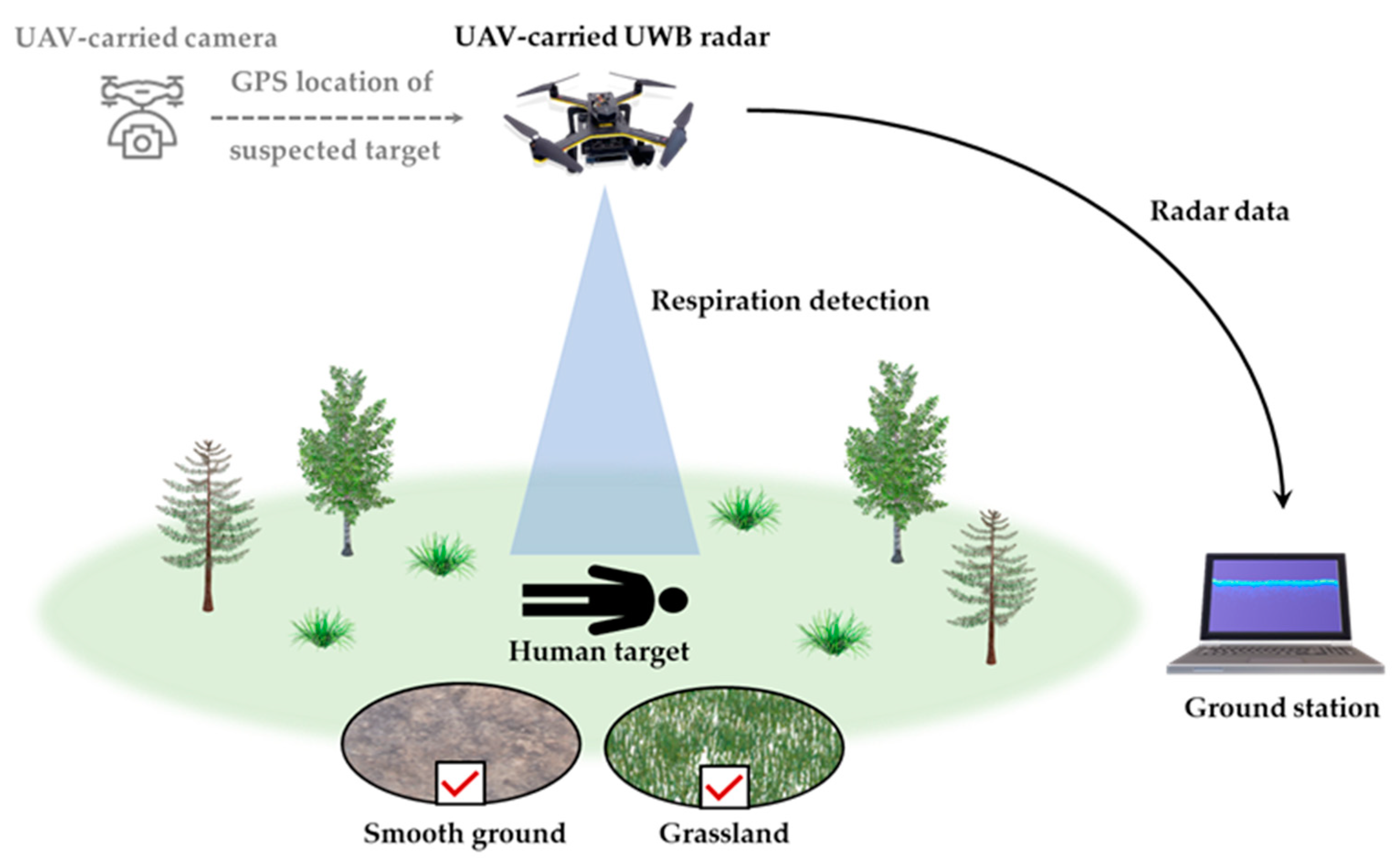
2. UAV-mounted UWB Radar System
3. Signal Model
4. Signal Processing
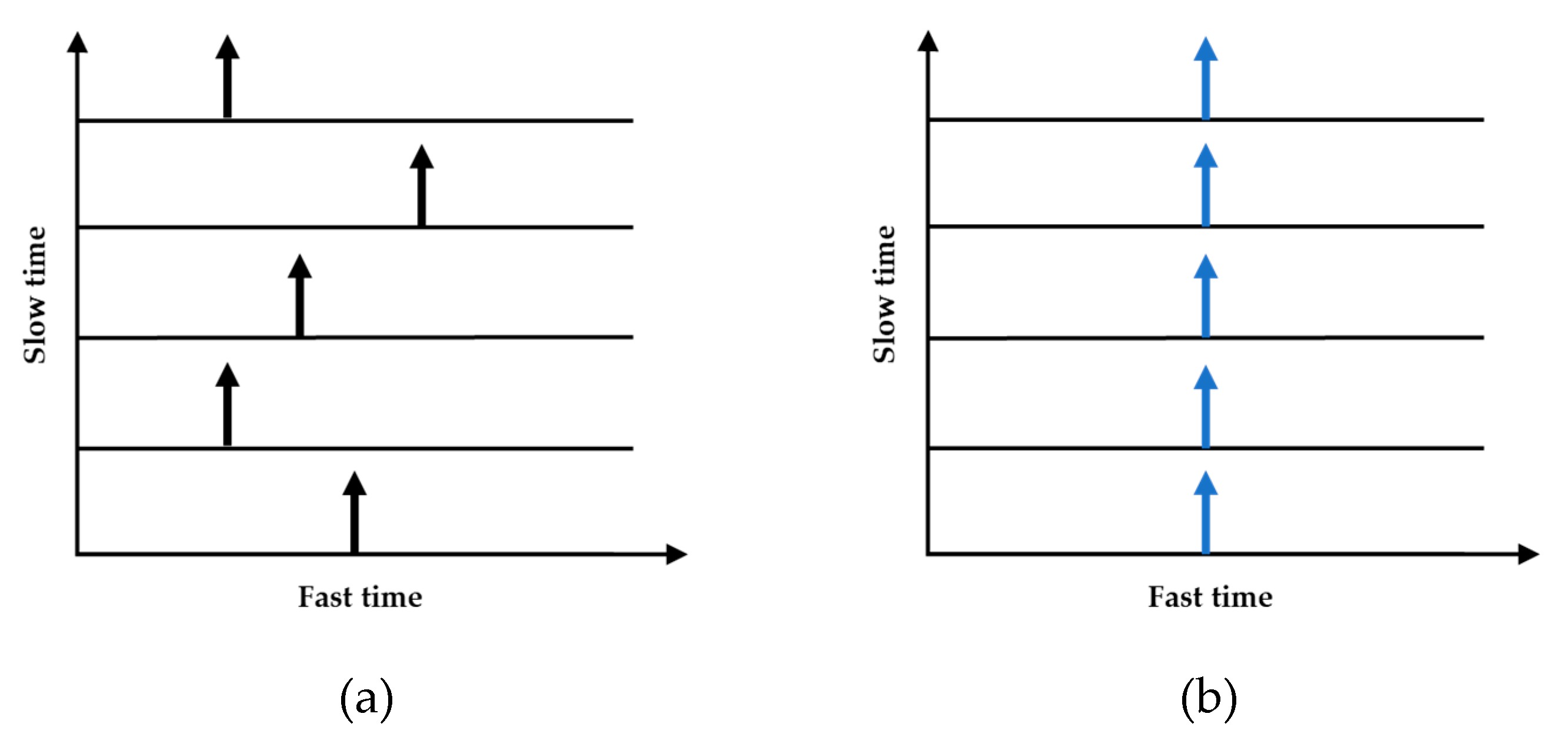
4.1. Range Migration Compensation
4.2. Observed Signals Extraction
4.3. Pre-Processing
4.4. Independent Component Analysis
4.4.1. ICA Compliance
4.4.2. Process of ICA
| Algorithm 1 FastICA |
| 1: Input the observed signals. |
| 2: Centre the data to give . 3: Whiten the data to give . 4: Choose the number of independent components m. 5: For 6: Initialize the weight vector 7: 8: 9: 10: If is not converged, go back to step 7. 11: End for 12: |
4.5. Respiratory Signal Extraction
5. Experiments
5.1. Experimental Setup
5.2. Results and Discussion
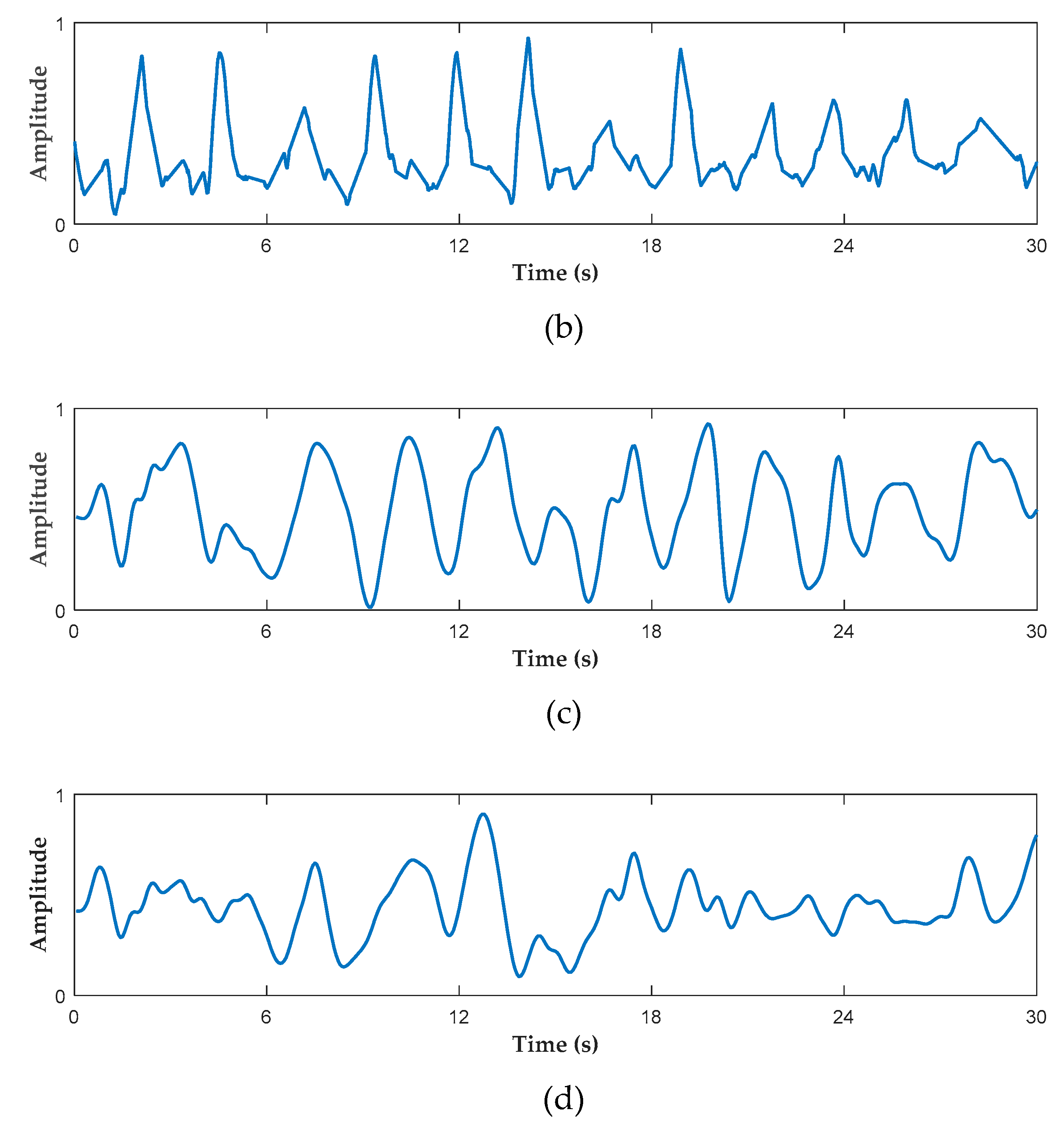
5.2.1. Observed Signals Extraction
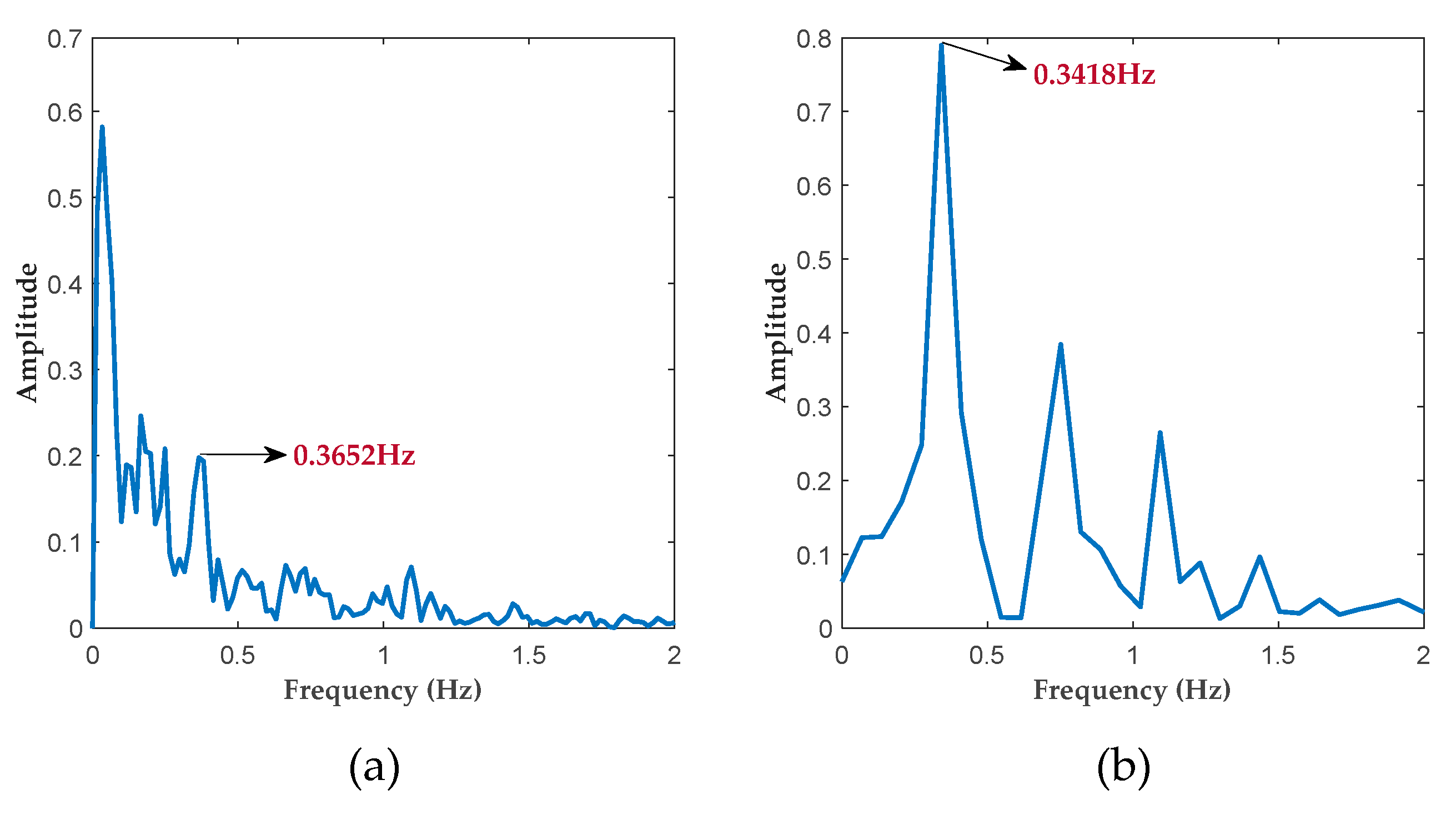
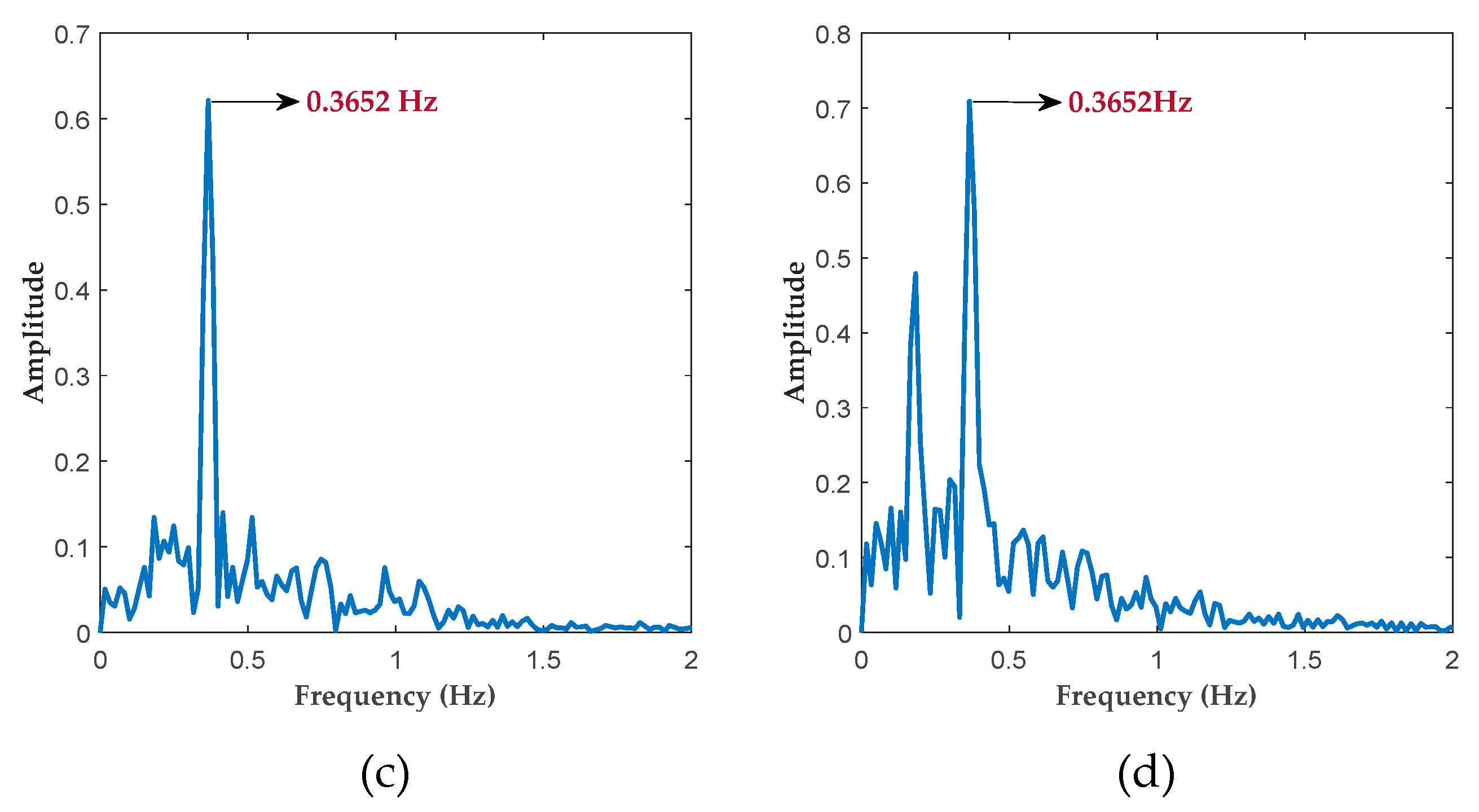
5.2.2. Respiration Detection in Scenario 1
5.2.3. Respiration Detection in Scenario 2
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Berawi, M.A.; Leviäkangas, P.; Siahaan, S.A.O.; Hafidza, A.; Sari, M.; Miraj, P.; Harwahyu, R.; Saroji, G. Increasing Disaster Victim Survival Rate: SaveMyLife Mobile Application Development. Int. J. Disaster Risk Reduct. 2021, 60, 102290. [Google Scholar] [CrossRef]
- Farahani, R.Z.; Lotfi, M.; Baghaian, A.; Ruiz, R.; Rezapour, S. Mass Casualty Management in Disaster Scene: A Systematic Review of OR&MS Research in Humanitarian Operations. Eur. J. Oper. Res. 2020, 287, 787–819. [Google Scholar]
- Qi, J.; Song, D.; Shang, H.; Wang, N.; Hua, C.; Wu, C.; Qi, X.; Han, J. Search and Rescue Rotary-wing UAV and its Application to the Lushan ms 7.0 Earthquake. J. Field Robot. 2016, 33, 290–321. [Google Scholar] [CrossRef]
- Tian, Y.; Liu, K.; Ok, K.; Tran, L.; Allen, D.; Roy, N.; How, J.P. Search and Rescue under the Forest Canopy Using Multiple UAVs. Int. J. Robot. Res. 2020, 39, 1201–1221. [Google Scholar] [CrossRef]
- Mohsan, S.A.H.; Khan, M.A.; Noor, F.; Ullah, I.; Alsharif, M.H. Towards the Unmanned Aerial Vehicles (UAVs): A Comprehensive Review. Drones 2022, 6, 147. [Google Scholar] [CrossRef]
- Kucharczyk, M.; Hugenholtz, C.H. Remote Sensing of Natural Hazard-related Disasters with Small Drones: Global Trends, Biases, and Research Opportunities. Remote Sens. Environ. 2021, 264, 112577. [Google Scholar] [CrossRef]
- Pensieri, M.G.; Garau, M.; Barone, P.M. Drones as an Integral Part of Remote Sensing Technologies to Help Missing People. Drones 2020, 4, 15. [Google Scholar] [CrossRef]
- Kundid Vasić, M.; Papić, V. Improving the Model for Person Detection in Aerial Image Sequences Using the Displacement Vector: A Search and Rescue Scenario. Drones 2022, 6, 19. [Google Scholar] [CrossRef]
- Xing, L.; Fan, X.; Dong, Y.; Xiong, Z.; Xing, L.; Yang, Y.; Bai, H.; Zhou, C. Multi-UAV Cooperative System for Search and Rescue based on YOLOv5. Int. J. Disaster Risk Reduct. 2022, 76, 102972. [Google Scholar] [CrossRef]
- Schedl, D.C.; Kurmi, I.; Bimber, O. An Autonomous Drone for Search and Rescue in Forests using Airborne Optical Section-ing. Sci. Robot. 2021, 6, 1188. [Google Scholar] [CrossRef]
- Jiang, C.; Ren, H.; Ye, X.; Zhu, J.; Zeng, H.; Nan, Y.; Sun, M.; Ren, X.; Huo, H. Object Detection from UAV Thermal Infrared Images and Videos using YOLO Models. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102912. [Google Scholar] [CrossRef]
- Qi, F.; Zhu, M.; Li, Z.; Lei, T.; Xia, J.; Zhang, L.; Yan, Y.; Wang, J.; Lu, G. Automatic Air-to-Ground Recognition of Outdoor Injured Human Targets Based on UAV Bimodal Information: The Explore Study. Appl. Sci. 2022, 12, 3457. [Google Scholar] [CrossRef]
- Cao, Y.; Qi, F.; Jing, Y.; Zhu, M.; Lei, T.; Li, Z.; Xia, J.; Wang, J.; Lu, G. Mission Chain Driven Unmanned Aerial Vehicle Swarms Cooperation for the Search and Rescue of Outdoor Injured Human Targets. Drones 2022, 6, 138. [Google Scholar] [CrossRef]
- Islam, S.M.; Lubecke, L.C.; Grado, C.; Lubecke, V.M. An Adaptive Filter Technique for Platform Motion Compensation in Unmanned Aerial Vehicle based Remote Life Sensing Radar. In Proceedings of the 2020 50th European Microwave Conference (EuMC), Utrecht, The Netherlands, 12–14 January 2021; pp. 937–940. [Google Scholar]
- Rong, Y.; Herschfelt, A.; Holtom, J.; Bliss, D.W. Cardiac and Respiratory Sensing from a Hovering UAV Radar Platform. In Proceedings of the 2021 IEEE Statistical Signal Processing Workshop (SSP), Rio de Janeiro, Brazil, 11–14 July 2021; pp. 541–545. [Google Scholar]
- Rohman, B.P.; Andra, M.B.; Nishimoto, M. Through-the-wall Human Respiration Detection Using UWB Impulse Radar on Hovering Drone. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6572–6584. [Google Scholar] [CrossRef]
- Wang, D.; Yoo, S.; Cho, S.H. Experimental comparison of IR-UWB radar and FMCW radar for vital signs. Sensors 2020, 20, 6695. [Google Scholar] [CrossRef]
- Liang, X.; Deng, J.; Zhang, H.; Gulliver, T.A. Ultra-wideband Impulse Radar Through-wall Detection of Vital Signs. Sci. Rep. 2018, 8, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Zhang, H.; Ye, S.; Fang, G.; Gulliver, T.A. Improved Denoising Method for Through-wall Vital Sign Detection Using UWB Impulse Radar. Digit. Signal Processing 2018, 74, 72–93. [Google Scholar] [CrossRef]
- Cardillo, E.; Li, C.; Caddemi, A. Vital Sign Detection and Radar Self-motion Cancellation Through Clutter Identification. IEEE Trans. Microw. Theory Tech. 2021, 69, 1932–1942. [Google Scholar] [CrossRef]
- Cardillo, E.; Li, C.; Caddemi, A. Empowering Blind People Mobility: A Millimeter-wave Radar Cane. In Proceedings of the 2020 IEEE International Workshop on Metrology for Industry 4.0 & IoT, Roma, Italy, 3–5 June 2020; pp. 213–217. [Google Scholar]
- Sharafi, A.; Baboli, M.; Eshghi, M.; Ahmadian, A. Respiration-rate Estimation of a Moving Target Using Impulse-based Ultra Wideband Radars. Australas. Phys. Eng. Sci. Med. 2012, 35, 31–39. [Google Scholar] [CrossRef]
- Xu, H.; Ebrahim, M.P.; Hasan, K.; Heydari, F.; Howley, P.; Yuce, M.R. Accurate Heart Rate and Respiration Rate Detection Based on a Higher-Order Harmonics Peak Selection Method Using Radar Non-Contact Sensors. Sensors 2021, 22, 83. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, P.; Huang, W.; Qi, F.; Liang, F.; Lv, H.; Yu, X.; Wang, J.; Zhang, Y. A Robust Multi-feature based Method for Distinguishing between Humans and Pets to Ensure Signal Source in Vital Signs Monitoring Using UWB Radar. EURASIP J. Adv. Signal Processing 2021, 2021, 1–24. [Google Scholar] [CrossRef]
- Ning, X.; Selesnick, I.W.; Duval, L. Chromatogram Baseline Estimation and Denoising Using Sparsity (BEADS). Chemom. Intell. Lab. Syst. 2014, 139, 156–167. [Google Scholar] [CrossRef]
- Calhoun, V.D.; Liu, J.; Adalı, T. A Review of Group ICA for FMRI Data and ICA for Joint Inference of Imaging, Genetic, and ERP Data. Neuroimage 2009, 45, S163–S172. [Google Scholar] [CrossRef]
- Ren, W.; Qi, F.; Foroughian, F.; Kvelashvili, T.; Liu, Q.; Kilic, O.; Long, T.; Fathy, A.E. Vital Sign Detection in Any Orientation Using a Distributed Radar Network via Modified Independent Component Analysis. IEEE Trans. Microw. Theory Tech. 2021, 69, 4774–4790. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Oja, E. Independent Component Analysis: Algorithms and Applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Hiroe, A. In Solution of Permutation Problem in Frequency Domain ICA, using Multivariate Probability Density Functions. In Proceedings of the International Conference on Independent Component Analysis and Signal Separation, Charleston, SC, USA, 5–8 March 2006; pp. 601–608. [Google Scholar]
- Zhang, S.; Zhao, C. Hybrid Independent Component Analysis (H-ICA) with Simultaneous Analysis of High-order and Second-order Statistics for Industrial Process Monitoring. Chemom. Intell. Lab. Syst. 2019, 185, 47–58. [Google Scholar] [CrossRef]
- Oja, E.; Yuan, Z. The FastICA Algorithm Revisited: Convergence Analysis. IEEE Trans. Neural Netw. 2006, 6, 1370–1381. [Google Scholar] [CrossRef] [PubMed]
- Contin, A.; Pastore, S. Classification and Separation of Partial Discharge Signals by Means of Their Auto-correlation Function Evaluation. IEEE Trans. Dielectr. Electr. Insul. 2009, 16, 1609–1622. [Google Scholar] [CrossRef]
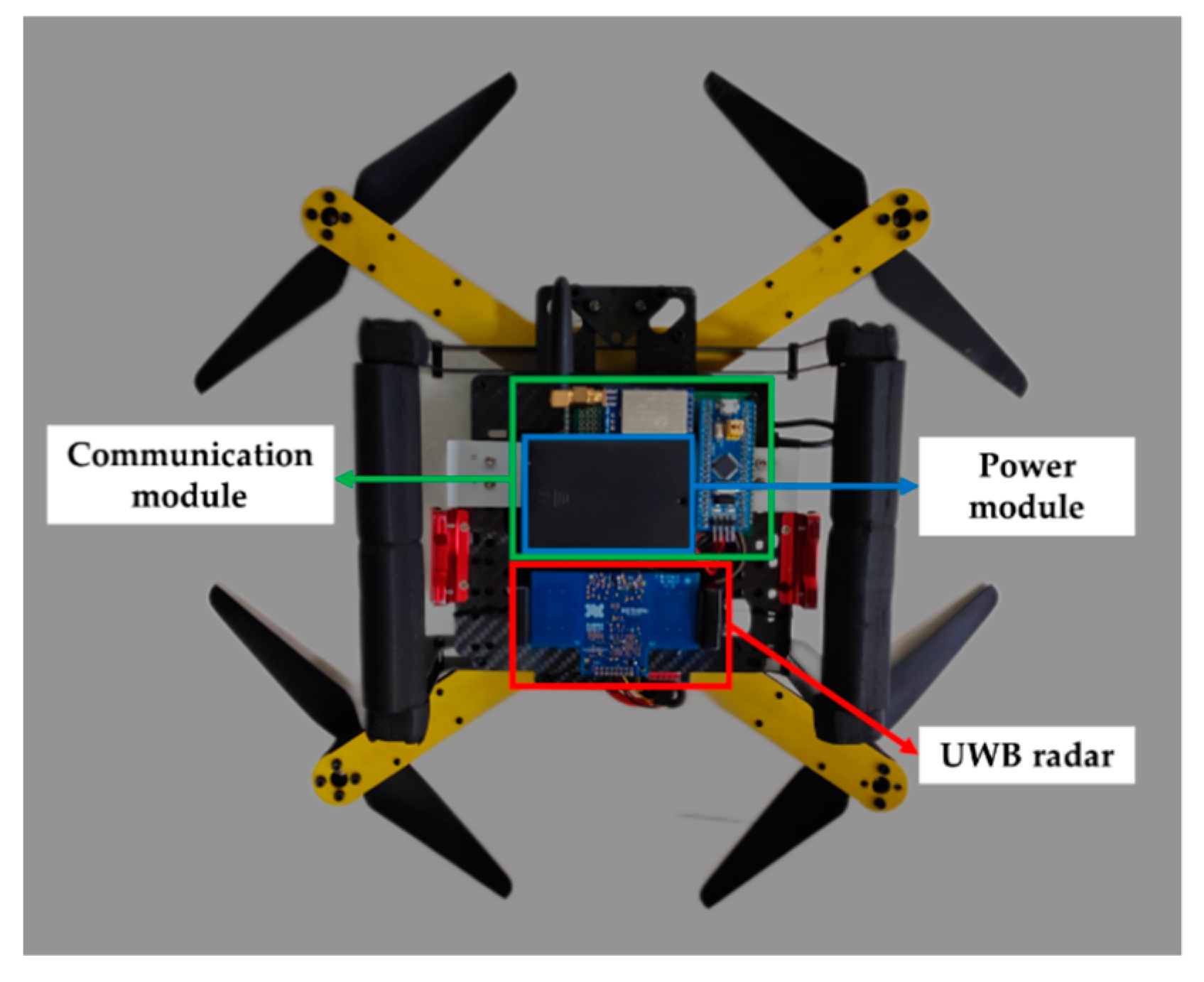








| Parameters | Values |
|---|---|
| Centre frequency | 7.29 GHz |
| Bandwidth | 1.4 GHz |
| Detection range | 0.4–5 m |
| Range resolution | 0.0514 m |
| Frame rate | 17 Hz |
| Scenario 1 | RR (Hz) | Accuracy (%) | SNR (dB) | ||||
|---|---|---|---|---|---|---|---|
| Reference | Our Method | BGR | Our Method | BGR | Our Method | BGR | |
| Subject 1 | 0.3418 | 0.3652 | 0.3652 | 93.15 | 93.15 | 15.82 | 10.56 |
| Subject 2 | 0.2032 | 0.2153 | 0.2210 | 94.05 | 91.24 | 16.18 | 11.49 |
| Subject 3 | 0.2889 | 0.2833 | 0.2833 | 98.05 | 98.05 | 15.27 | 11.35 |
| Scenario 2 | RR (Hz) | Accuracy (%) | SNR (dB) | ||||
|---|---|---|---|---|---|---|---|
| Reference | Our Method | BGR | Our Method | BGR | Our Method | BGR | |
| Subject 1 | 0.4329 | 0.4482 | 0.1268 | 96.47 | 29.29 | 6.69 | 5.48 |
| Subject 2 | 0.2930 | 0.2988 | 0.3682 | 98.02 | 74.33 | 7.38 | 5.95 |
| Subject 3 | 0.2500 | 0.2656 | 0.4016 | 93.76 | 39.36. | 6.74 | 4.92 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, Y.; Qi, F.; Yang, F.; Cao, Y.; Zhu, M.; Li, Z.; Lei, T.; Xia, J.; Wang, J.; Lu, G. Respiration Detection of Ground Injured Human Target Using UWB Radar Mounted on a Hovering UAV. Drones 2022, 6, 235. https://doi.org/10.3390/drones6090235
Jing Y, Qi F, Yang F, Cao Y, Zhu M, Li Z, Lei T, Xia J, Wang J, Lu G. Respiration Detection of Ground Injured Human Target Using UWB Radar Mounted on a Hovering UAV. Drones. 2022; 6(9):235. https://doi.org/10.3390/drones6090235
Chicago/Turabian StyleJing, Yu, Fugui Qi, Fang Yang, Yusen Cao, Mingming Zhu, Zhao Li, Tao Lei, Juanjuan Xia, Jianqi Wang, and Guohua Lu. 2022. "Respiration Detection of Ground Injured Human Target Using UWB Radar Mounted on a Hovering UAV" Drones 6, no. 9: 235. https://doi.org/10.3390/drones6090235
APA StyleJing, Y., Qi, F., Yang, F., Cao, Y., Zhu, M., Li, Z., Lei, T., Xia, J., Wang, J., & Lu, G. (2022). Respiration Detection of Ground Injured Human Target Using UWB Radar Mounted on a Hovering UAV. Drones, 6(9), 235. https://doi.org/10.3390/drones6090235






