Stability Derivatives of Various Lighter-than-Air Vehicles: A CFD-Based Comparative Study
Abstract
1. Introduction
2. Stability Derivatives’ Extraction Methodology
2.1. Pure Surge Oscillations
2.2. Pure Heave Oscillations
2.3. Pure Pitch Oscillations
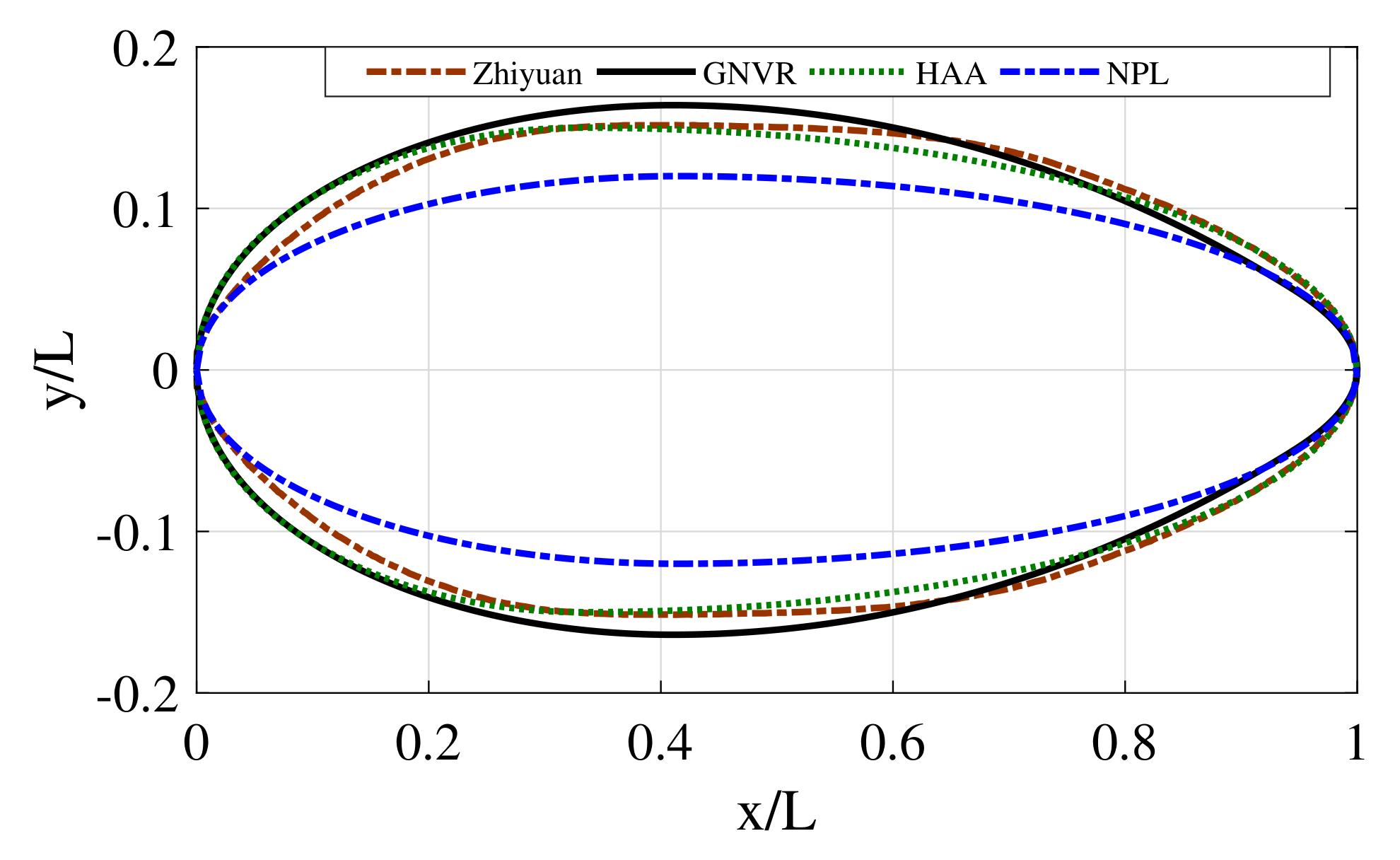
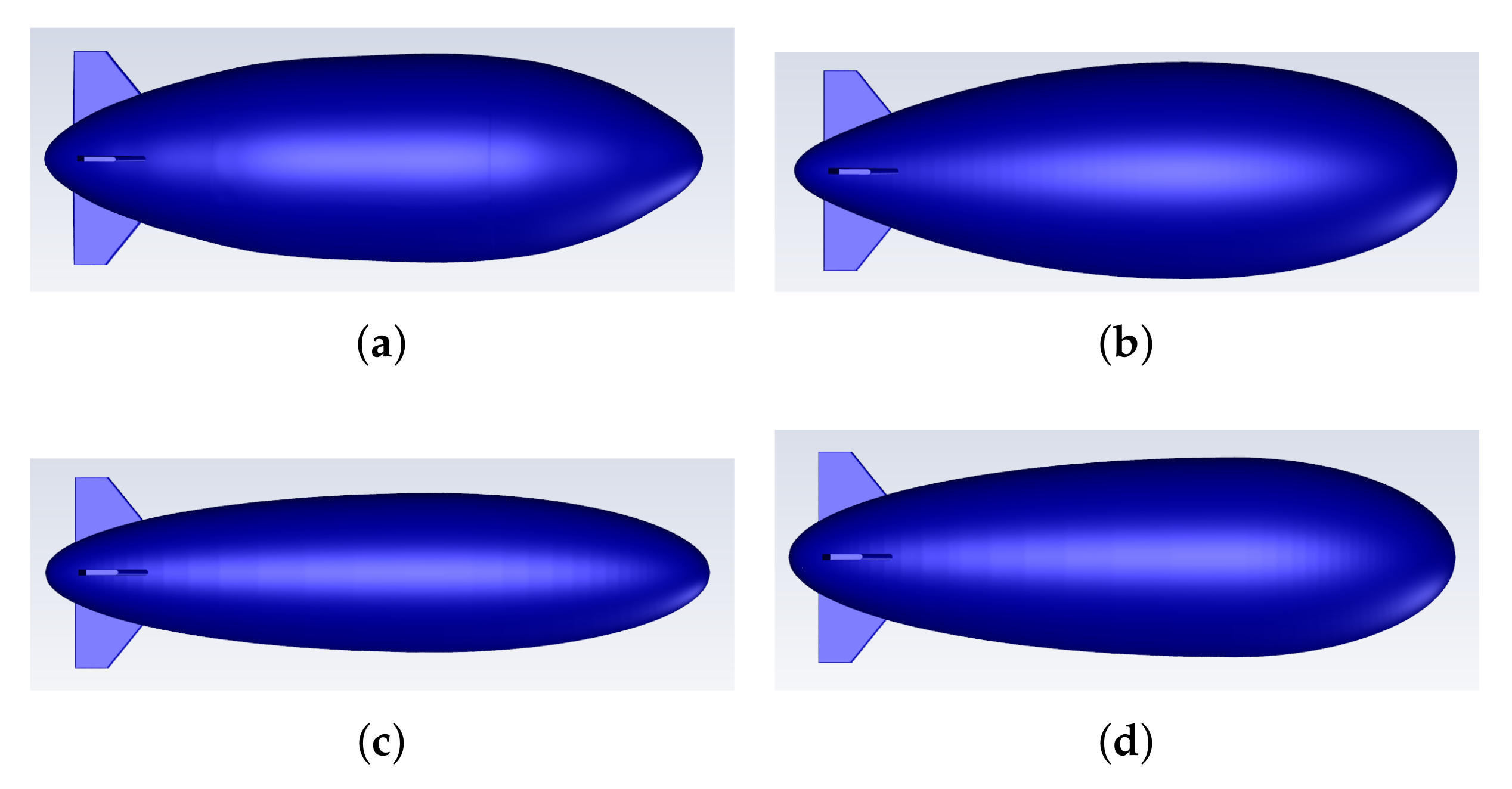
3. Aerostat Shapes
4. Numerical Simulation
4.1. Governing Equations
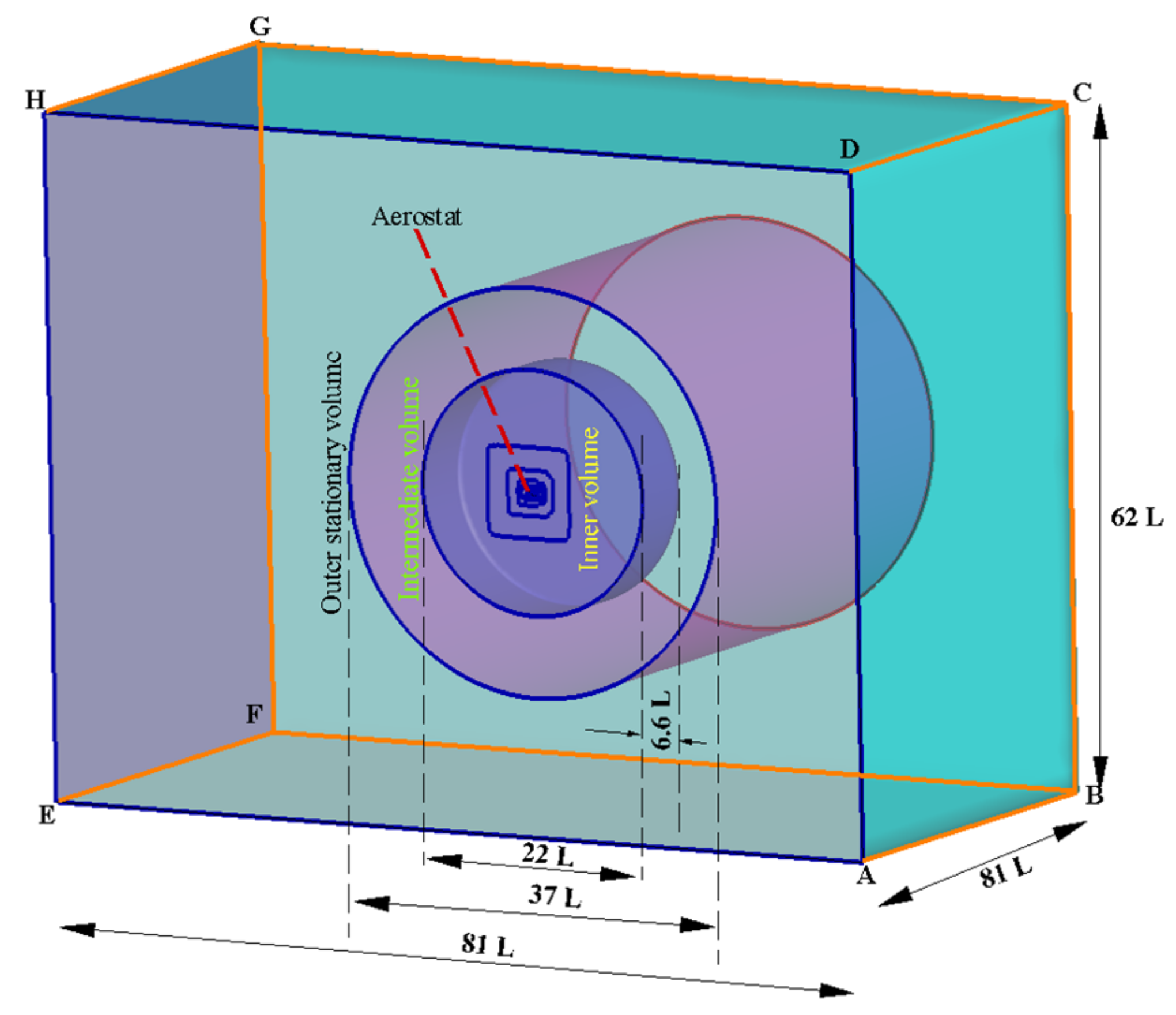
4.2. Computational Setup—Domain and Mesh
4.3. Simulation Details
5. Simulation Results
5.1. Grid and Time Step Independence Study
5.2. Validation of the Grid Motion
5.3. Validation of the Stability Derivative Extraction Methodology
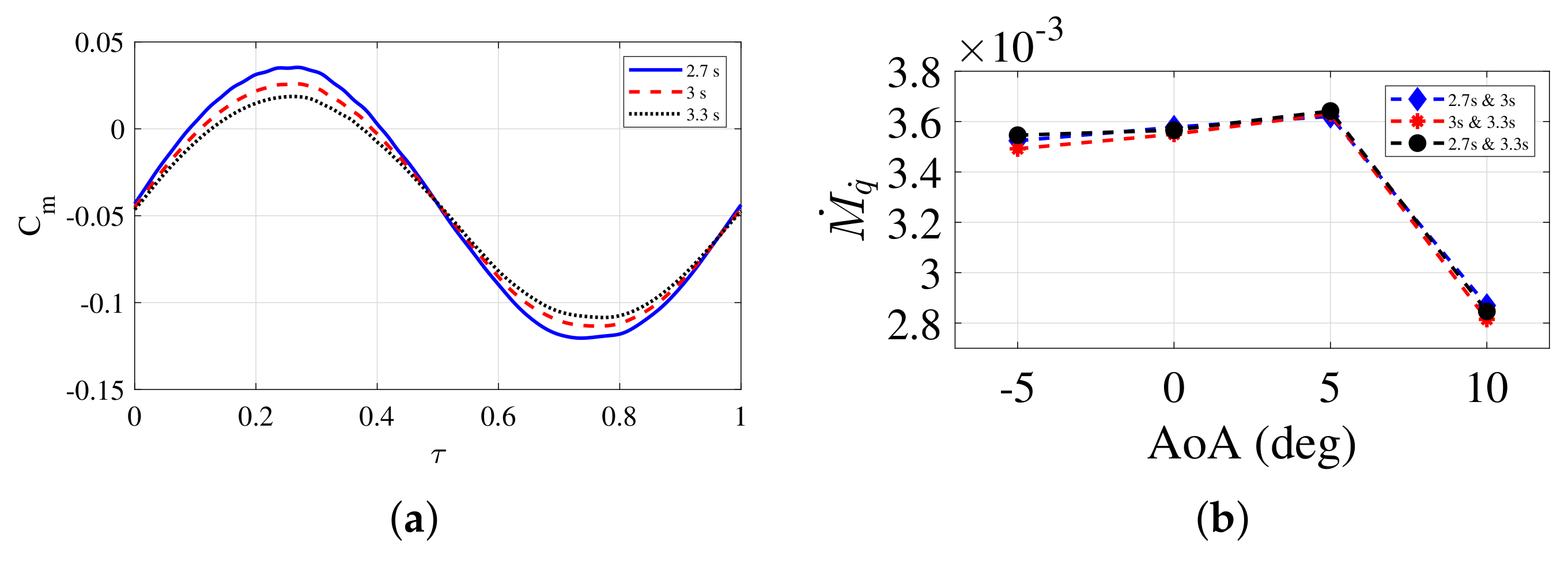
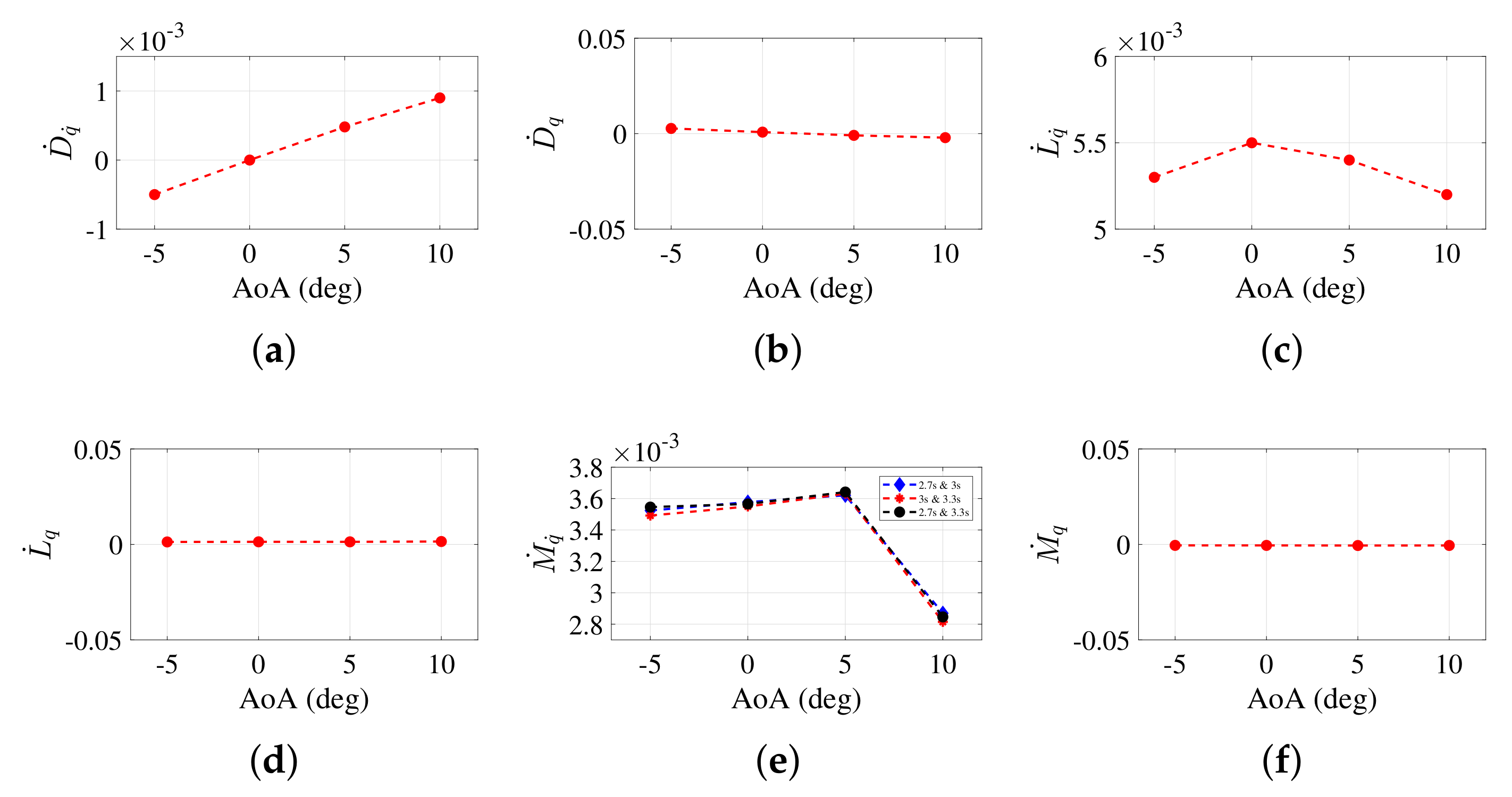
5.4. Acceleration and Frequency Independence Study
5.5. Static Aerodynamic Characteristics
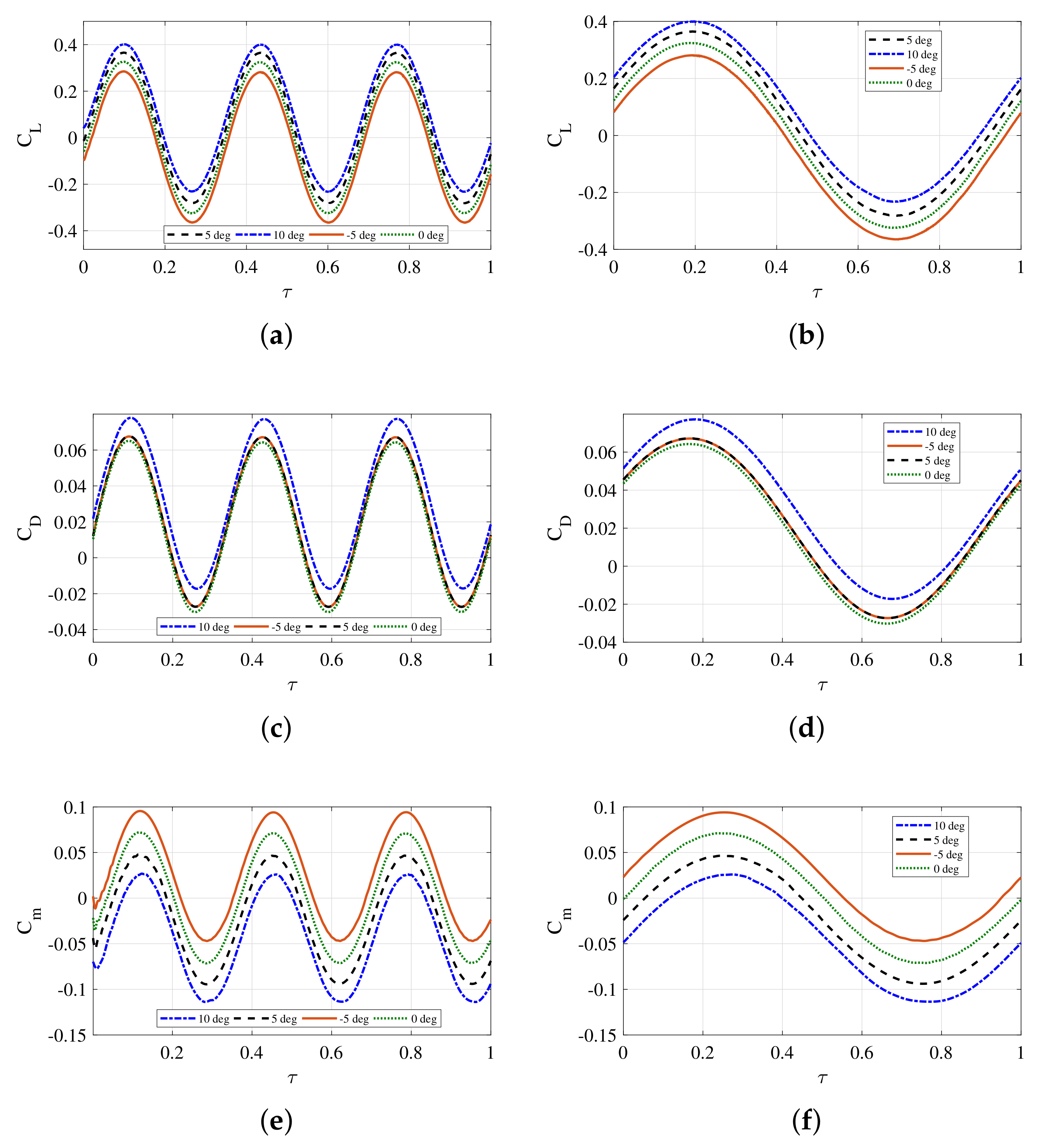
5.6. Dynamic Stability Derivatives
5.6.1. Zhiyuan Aerostat
5.6.2. GNVR, HAA and NPL Aerostats
6. Conclusions of the Study
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Allison, S.; Bai, H.; Jayaraman, B. Wind estimation using quadcopter motion: A machine learning approach. Aerosp. Sci. Technol. 2020, 98, 105699. [Google Scholar] [CrossRef]
- Beaucage, P.; Lafrance, G.; Lafrance, J.; Choisnard, J.; Bernier, M. Synthetic aperture radar satellite data for offshore wind assessment: A strategic sampling approach. J. Wind Eng. Ind. Aerodyn. 2011, 99, 27–36. [Google Scholar] [CrossRef]
- Schmitt, N.P.; Rehm, W.; Pistner, T.; Zeller, P.; Diehl, H.; Navé, P. The AWIATOR airborne LIDAR turbulence sensor. Aerosp. Sci. Technol. 2007, 11, 546–552. [Google Scholar] [CrossRef]
- Grillo, C.; Montano, F. Wind component estimation for UAS flying in turbulent air. Aerosp. Sci. Technol. 2019, 93, 105317. [Google Scholar] [CrossRef]
- Anoop, S.; Velamati, R.K.; Oruganti, V.R.M.; Mohammad, A. Computational analysis of the aerodynamic characteristics and stability derivatives of an aerostat under unsteady wind conditions. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 225. [Google Scholar] [CrossRef]
- Satapathy, J.; Bhat, G.S. Studies of Extreme Gust Storm Events in Bengaluru, India. Curr. Sci. 2020, 119, 343–351. [Google Scholar] [CrossRef]
- Santos, L.; Marques, F. Nonlinear aeroelastic analysis of airfoil section under stall flutter oscillations and gust loads. J. Fluids Struct. 2021, 102, 103250. [Google Scholar] [CrossRef]
- Akhlaghi, H.; Soltani, M.R.; Maghrebi, M.J. Transitional boundary layer study over an airfoil in combined pitch-plunge motions. Aerosp. Sci. Technol. 2020, 98, 105694. [Google Scholar] [CrossRef]
- Anoop, S.; Velamati, R.K.; Oruganti, V.R.M. Aerodynamic characteristics of an aerostat under unsteady wind gust conditions. Aerosp. Sci. Technol. 2021, 113, 106684. [Google Scholar] [CrossRef]
- Mueller, J.; Paluszek, M.; Zhao, Y. Development of an Aerodynamic Model and Control Law Design for a High Altitude Airship. In Proceedings of the AIAA 3rd “Unmanned Unlimited” Technical Conference, Workshop and Exhibit, Chicago, IL, USA, 20–23 September 2004. [Google Scholar] [CrossRef]
- Jones, S.P.; DeLaurier, J.D. Aerodynamic estimation techniques for aerostats and airships. J. Aircr. 1983, 20, 120–126. [Google Scholar] [CrossRef]
- Ashraf, M.; Choudhry, M. Dynamic modeling of the airship with Matlab using geometrical aerodynamic parameters. Aerosp. Sci. Technol. 2013, 25, 56–64. [Google Scholar] [CrossRef]
- Anoop, S.; Oruganti, V.R.M. Modelling and simulation of aerodynamic parameters of an airship. Adv. Sci. Technol. Eng. Syst. J. 2020, 5, 167–176. [Google Scholar] [CrossRef]
- Mahmood, K.; Ismail, N.A. Application of multibody simulation tool for dynamical analysis of tethered aerostat. J. King Saud Univ. Eng. Sci. 2020, 34, 209–216. [Google Scholar] [CrossRef]
- Anoop, S.; Ramana Murthy, O.V.; Sharma, K.R. Analysis of Airship Dynamics using Linear Quadratic Regulator Controller. In Proceedings of the 15th IEEE India Council International Conference (INDICON), Coimbatore, India, 16–18 December 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Zhao, L.; Liu, S.; Yan, J.; Ge, Y. Aerodynamic modeling for streamlined box girders using nonlinear differential equations and validation in actively generated turbulence. Wind Struct. Int. J. 2021, 33, 71–86. [Google Scholar] [CrossRef]
- Nguyen, K.; Au, L.T.K.; Phan, H.V.; Park, H.C. Comparative dynamic flight stability of insect-inspired flapping-wing micro air vehicles in hover: Longitudinal and lateral motions. Aerosp. Sci. Technol. 2021, 119, 107085. [Google Scholar] [CrossRef]
- Bykerk, T.; Verstraete, D.; Steelant, J. Low speed lateral-directional aerodynamic and static stability analysis of a hypersonic waverider. Aerosp. Sci. Technol. 2020, 98, 105709. [Google Scholar] [CrossRef]
- Bryan, G. Stability in Aviation: An Introduction to Dynamical Stability as Applied to the Motions of Aeroplanes; Macmillan and Company, Limited: New York, NY, USA, 1911. [Google Scholar]
- Mi, B.G.; Zhan, H. Review of Numerical Simulations on Aircraft Dynamic Stability Derivatives. Arch. Comput. Methods Eng. 2019, 27, 1515–1544. [Google Scholar] [CrossRef]
- Khoury, G. Airship Technology; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Wu, Y.; Li, L.; Su, X.; Gao, B. Dynamics modeling and trajectory optimization for unmanned aerial-aquatic vehicle diving into the water. Aerosp. Sci. Technol. 2019, 89, 220–229. [Google Scholar] [CrossRef]
- Bykerk, T.; Verstraete, D.; Steelant, J. Low speed longitudinal dynamic stability analysis of a hypersonic waverider using unsteady Reynolds averaged Navier Stokes forced oscillation simulations. Aerosp. Sci. Technol. 2020, 103, 105883. [Google Scholar] [CrossRef]
- Badesha, S. Aerodynamics of the TCOM 71M aerostat. In Proceedings of the 10th Lighter-Than-Air Systems Technology Conference, Scottsdale, AZ, USA, 14–16 September 1993; pp. 1–4. [Google Scholar] [CrossRef]
- Ignatyev, D.I.; Khrabrov, A.N. Neural network modeling of unsteady aerodynamic characteristics at high angles of attack. Aerosp. Sci. Technol. 2015, 41, 106–115. [Google Scholar] [CrossRef]
- Waqar, A.; Ali, O.A.; Erwin, S.; Mohamed, A.J. Wind tunnel testing of hybrid buoyant aerial vehicle. Aircr. Eng. Aerosp. Technol. 2017, 89, 174–180. [Google Scholar] [CrossRef]
- Tao, Q.; Tan, T.J.; Cha, J.; Yuan, Y.; Zhang, F. Modeling and Control of Swing Oscillation of Underactuated Indoor Miniature Autonomous Blimps. Unmanned Syst. 2021, 9, 73–86. [Google Scholar] [CrossRef]
- Junior, J.L.M.; Santos, J.S.; Morales, M.A.; Goes, L.C.; Stevanovic, S.; Santana, R.A. Airship Aerodynamic Coefficients Estimation Based on Computational Method for Preliminary Design. In Proceedings of the AIAA Aviation Forum, Dallas, TX, USA, 17–21 June 2019. [Google Scholar] [CrossRef]
- Ullah, A.; Badar Zaman, M.; Aashan Bhatti, M.; Qasim, D.; Hamid, A.; Xiong, Q.; Khan, A. CFD study of drag and lift coefficients of non-spherical particles. J. King Saud. Univ. Eng. Sci. 2021, in press. [Google Scholar] [CrossRef]
- Wang, X.L. Computational Fluid Dynamics Predictions of Stability Derivatives for Airship. J. Aircr. 2012, 49, 933–940. [Google Scholar] [CrossRef]
- Ronch, A.D.; Vallespin, D.; Ghoreyshi, M.; Badcock, K.J. Evaluation of Dynamic Derivatives Using Computational Fluid Dynamics. AIAA J. 2012, 50, 470–484. [Google Scholar] [CrossRef]
- Ronch, A.D. On the Calculation of Dynamic Derivatives Using Computational Fluid Dynamics. Ph.D. Thesis, University of Liverpool, Liverpool, UK, 2012. [Google Scholar]
- Carrión, M.; Biava, M.; Barakos, G.N.; Stewart, D. Study of Hybrid Air Vehicle Stability Using Computational Fluid Dynamics. J. Aircr. 2017, 54, 1328–1339. [Google Scholar] [CrossRef][Green Version]
- Lee, S.K.; Joung, T.H.; Cheo, S.J.; Jang, T.S.; Lee, J.H. Evaluation of the added mass for a spheroid-type unmanned underwater vehicle by vertical planar motion mechanism test. Int. J. Nav. Archit. Ocean Eng. 2011, 3, 174–180. [Google Scholar] [CrossRef]
- Mader, C.A.; Martins, J.R.R.A. Computing Stability Derivatives and Their Gradients for Aerodynamic Shape Optimization. AIAA J. 2014, 52, 2533–2546. [Google Scholar] [CrossRef]
- Muller, L.; Libsig, M.; Martinez, B.; Bastide, M.; Bidino, D.; Yannick, B.; Roy, J.C. Wind tunnel measurements of the dynamic stability derivatives of a fin-stabilized projectile by means of a 3-axis freely rotating test bench. In Proceedings of the AIAA Aviation Forum, Virtual, 15–19 June 2020. [Google Scholar] [CrossRef]
- Javanmard, E.; Mansoorzadeh, S.; Mehr, J.A. A new CFD method for determination of translational added mass coefficients of an underwater vehicle. Ocean Eng. 2020, 215, 107857. [Google Scholar] [CrossRef]
- Ghoreyshi, M.; Jirásek, A.; Cummings, R.M. Reduced order unsteady aerodynamic modeling for stability and control analysis using computational fluid dynamics. Prog. Aerosp. Sci. 2014, 71, 167–217. [Google Scholar] [CrossRef]
- Kale, S.; Joshi, P.; Pant, R. A generic methodology for determination of drag coefficient of an aerostat envelope using CFD. In Proceedings of the AIAA 5th ATIO and 16th Lighter-Than-Air Sys Tech. and Balloon Systems Conferences, Arlington, VA, USA, 26–28 September 2005. [Google Scholar] [CrossRef]
- Liang, H.; Zhu, M.; Guo, X.; Zheng, Z. Conceptual Design Optimization of High Altitude Airship in Concurrent Subspace Optimization. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, Tennessee, 9–12 January 2012. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, X.; Zhang, B.; Zheng, W.; Wang, Y. Bionic design for the aerodynamic shape of a stratospheric airship. Aerosp. Sci. Technol. 2020, 98, 105664. [Google Scholar] [CrossRef]
- Wang, Q.B.; Chen, J.A.; Fu, G.Y.; Duan, D.P. An approach for shape optimization of stratosphere airships based on multidisciplinary design optimization. J. Zhejiang Univ. Sci. A Appl. Phys. Eng. 2009, 10, 1609–1616. [Google Scholar] [CrossRef]
- ANSYS. Academic Research FLUENT, Release 20.2, Help System, Fluent Theory Manual; ANSYS, Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- Olsen, J. Compendium of Unsteady Aerodynamic Measurements; AGARD-R-702 Report; North Atlantic Treaty Organization (NATO) Advisory Group for Aerospace Research and Development: London, UK, 1982. [Google Scholar]
- Korotkin, A. Added Masses of Ship Structures; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009; Volume 88. [Google Scholar] [CrossRef]










| Simulation | Shape | Gust | AoA (deg) | Amplitude | Time Period (s) |
|---|---|---|---|---|---|
| Grid independence | Zhi | IEC/Sine | 10 | 12.5 m/s | 10.5 |
| Time step independence | Zhi | IEC/Sine | 10 | 12.5 m/s | 10.5 |
| Mesh motion validation | NACA-0012 | Sine | 0.5 to 5 | 2.4 deg | 0.12 |
| Method validation | Spheroid | Sine | 0 | 1 m/s | 1.6 |
| Acceleration independence | Zhi | Sine | 10 | 0.5, 0.75, 1 m/s | 3 |
| Frequency independence | Zhi | Sine | 10 | 5 deg | 2.7, 3, 3.3 |
| Surge motion | Zhi, HAA, GNVR, NPL | Sine | −5, 0, 5, 10 | 1 m/s | 3 |
| Heave motion | Zhi, HAA, GNVR, NPL | Sine | −5, 0, 5, 10 | 1 m/s | 3 |
| Pitch motion | Zhi, HAA, GNVR, NPL | Sine | −5, 0, 5, 10 | 5 deg | 2.7, 3, 3.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sasidharan, A.; Velamati, R.K.; Janardhanan, S.; Oruganti, V.R.M.; Mohammad, A. Stability Derivatives of Various Lighter-than-Air Vehicles: A CFD-Based Comparative Study. Drones 2022, 6, 168. https://doi.org/10.3390/drones6070168
Sasidharan A, Velamati RK, Janardhanan S, Oruganti VRM, Mohammad A. Stability Derivatives of Various Lighter-than-Air Vehicles: A CFD-Based Comparative Study. Drones. 2022; 6(7):168. https://doi.org/10.3390/drones6070168
Chicago/Turabian StyleSasidharan, Anoop, Ratna Kishore Velamati, Sheeja Janardhanan, Venkata Ramana Murthy Oruganti, and Akram Mohammad. 2022. "Stability Derivatives of Various Lighter-than-Air Vehicles: A CFD-Based Comparative Study" Drones 6, no. 7: 168. https://doi.org/10.3390/drones6070168
APA StyleSasidharan, A., Velamati, R. K., Janardhanan, S., Oruganti, V. R. M., & Mohammad, A. (2022). Stability Derivatives of Various Lighter-than-Air Vehicles: A CFD-Based Comparative Study. Drones, 6(7), 168. https://doi.org/10.3390/drones6070168








