1. Introduction
Due to the advantages of powerful execution and low risk to human life, UAVs have been widely used for various military purposes such as reconnaissance, precision strike, surveillance, communication relay, decoy, etc. [
1]. Compared with a single UAV, UAVs with different capacities can achieve more complicated mission goals through cooperation. Nowadays, there is a growing consensus that mission planning, which is generally composed of task assignment and path planning, should be taken as the core technique to improve the combat efficiency [
2,
3].
The task assignment problem is essentially a nondeterministic polynomial hard (NP-hard) problem [
4], which suggests that the scale of the problem severely impacts the solving process. The multi-UAV task assignment problem can generally be modeled as a mixed-integer linear programming (MILP), and commonly used models include vehicle routing problem (VRP) [
5], multiple traveling salesman problem (MTSP) [
6], multiple processors resource allocation (MPRA) [
7], etc. Complicated constraints are embedded in the models to give an accurate description of the mission. The exhaustive enumerations of MILP and the tree search method lead to prohibitive computational complexity when handling large and complex missions [
8,
9]. Instead, due to the powerful optimality-seeking ability and extraordinary computational stability, swarm intelligence algorithms (SIAs) have become the mainstream. Commonly used SIAs in these fields include particle swarm optimization (PSO) [
10], genetic algorithm (GA) [
11,
12], ant colony optimization (ACO) [
13,
14], reactive tabu search algorithm [
15] and their variations. In order to improve the solving performance, many studies combine multiple SIAs to construct novel compound methods [
16,
17]. In addition to the centralized algorithms mentioned above, distributed task assignment methods such as contract net [
18], auction methods [
19] are also popular for their advantages in real-time implementation.
When the factors considered are different, the model of the task assignment problem and the corresponding algorithm are different. These factors may include the types of UAVs, the types of tasks, and the types of constraints, etc. For the multi-UAV collaborative task assignment problem, Jia et al. [
20] proposed the two-parent genetic algorithm based on the given coding scheme and a sequence number cross method. Considering the task coupling constraints, the resource constraints and the strict task precedence constraint comprehensively, Ye et al. [
21] established a cooperative multiple task assignment model to minimize the makespan, and an adaptive genetic algorithm is developed to address the problem (note that makespan is often used in scheduling problems, where it represents the total execution time of UAV tasks). Taking the benefits of UAVs, the time required to execute tasks and the task load into account, Yang et al. [
22] proposed a hybrid task allocation method for the multi-UAV cooperative task allocation, where the quantum genetic algorithm, the grouping optimization strategy and the simulated annealing criterion are considered in the proposed method. Zhen et al. [
23] proposed an intelligent self-organized algorithm to solve the cooperative task planning problem, which the maneuverability constraints, the collision avoidance constraints, the threat avoidance constraints and the range constraints are considered. Environmental uncertainty also affects models and algorithms. Bertuccelli et al. [
24] studied the real-time multi-UAV task assignment in dynamic and uncertain environment, and analyzed task assignment for heterogeneous air vehicles using a guaranteed conflict-free assignment algorithm. Considering the stochastic velocities of UAVs, Jia et al. [
25] studied the cooperative multiple task assignment problem, which is formulated as a two-stage stochastic programming model, and proposed an improved genetic algorithm. A task assignment problem that many criteria values essential to task assignment were random or fuzzy was studied in the literature [
26], and a novel approach based on stochastic multicriteria acceptability analysis method was proposed in this study. There are many other related studies on the consideration of uncertain factors in the task assignment of multiple UAVs [
27,
28,
29,
30], which will not be described in detail here.
It should be noted that general crossover and mutation operations in SIAs are likely to generate chromosome with constraint violation, which results in the deadlock (or “lock” for short) phenomenon. Each algorithm has its mechanism to fix these infeasible solutions, known as the unlocking process. During the implementation, a large portion of computational time is consumed by the unlocking process. For example, unlocking process is achieved by keeping swapping two columns of the chromosome randomly until all constraints are satisfied in [
31]. It results in an unacceptable computational burden as the problem scale increases. Hence, developing efficient unlock mechanisms is significantly beneficial for improving the computational efficiency.
Considering the complexity in the both spatial and time domain of modern air warfare, CRJOs are frequently executed to cover the battlefield with a vast range. It may require heterogeneous UAVs distributed at different bases to constitute a fleet or a swarm to achieve certain mission goals cooperatively. For example, aiming to attack an island, the carrier-based combat UAVs on the sea and the bomber UAVs at home should cooperate, where the former tries to win the air superiority and the latter executes bombing missions. However, task assignment problems under the multi-base scenario are rarely seen in previous research. Hence, in this paper, we address the cooperative task assignment for multiple heterogeneous UAVs in CRJOs by an IGA. First, the task assignment problem is formulated into a multi-objective MILP. In the developed mathematical model, heterogeneous UAVs set off from different airports and they are not required to return exactly to the airport they depart. Three types of tasks (i.e., classification, attack, and verification) are expected to be executed sequentially on each target. Each target is prescribed with a fixed value, and it allows multiple attacks on a certain target. Two contradictory objectives, i.e., minimization of execution time and maximization of obtained value expectation are set. Practical constraints such as maximum ammunition load, time constraints, and so on are imposed. In addition, the ammunition inventory of each airport, which is rarely seen in the existing literature, is also taken into consideration. To solve the problem, an IGA is developed. It deals with various constraints in the formulated problem through a unique encoding of chromosomes and specifically designed resource constraint sets (RCSs). Special crossover and mutation operations can adaptively adjust the number of attacks on the target according to the fitness function. Furthermore, the logic-based unlocking method greatly reduces the time consumption of unlocking process and effectively improves the efficiency of the algorithm.
To the best of our knowledge, this is the first paper to address the problem of multi-heterogeneous UAV mission assignment with multiple airports and munitions inventory constraints. The main contributions of this paper can be summarized as follows: (i) a novel IGA with a special encoding format and genetic operations is developed to solve the problem; (ii) an efficient logic-based unlocking mechanism is designed by using RCS; and (iii) the number of attacks on the target can be determined by the IGA without the need of prior setting.
The remainder of the paper is organized as follows.
Section 2 describes the multi-airport task assignment problem.
Section 3 establishes the corresponding MILP model. An IGA to solve the problem is developed in
Section 4 and then validated in
Section 5. Finally,
Section 6 concludes the paper.
2. Problem Description
Suppose that
detected targets with known positions in the battlefield. Let
denote the set of targets. Target
is assigned with a value
. For a target, a series of sub-tasks need to be performed on it until the desired goal is reached. Each target contains 3 types of tasks, that is, classification task, attack task and verification task. Let
k represent the task type,
, respectively, represent classification task, attack task and verification task. In particular, let
represents that the UAV returns to the airport. In addition,
represents the number of task types, thus,
.
For simplicity of description, the classification, attack and verification tasks are abbreviated as
C,
A,
V, respectively. Let
be the task set of target
,
where
is the number of attack tasks of target
, which depends on the value of the target
. In this paper, the values of
are quantities to be optimized rather than being prescribed. Since multiple airports are considered, we suppose that
denote the set of airports, where
is the
m-th airport.
According to the actual situation, for the same target, classification, attack and verification tasks should be executed sequentially. Let
,
,
denote the execution time of the task
C,
,
V of target
, respectively. Then, we have,
where
,
.
Three types of UAVs, i.e., surveillance UAV, combat UAV and munition UAV cooperate to conduct the CRJO. Among them, surveillance UAVs can perform the classification and verification tasks, combat UAVs can perform all types of tasks, and munition UAVs can only perform the attack task. Let
denote the set of UAVs, where
is the
i-th UAV. The tasks assigned to a certain UAV constitute the task set of the UAV. Each UAV loads ammunition at the airport and then takes off to perform its tasks. Suppose that the task set of UAV
is
where
,
is the
n-th task of UAV
. Each UAV completes the tasks one by one in the order of task assignment. Let
denote the execution time of the
n-th task of UAV
. Then, we have,
There is the possibility, in practical situations, that a UAV does not completely destroy a target by one attack. In this paper, we assume that each UAV has different success probabilities when attacking different targets. Let the probability of target being destroyed by UAV is written as . We only consider the success probability of the attack task.In addition, for the cross-regional joint operations problem, we also make the following assumptions:
To reduce the complexity of the problem, the environment considered is a two-dimensional plane;
UAVs all fly at different altitudes, and there will be no collision even if the trajectories overlap;
The success rate in performing classification and verification tasks is 100%.
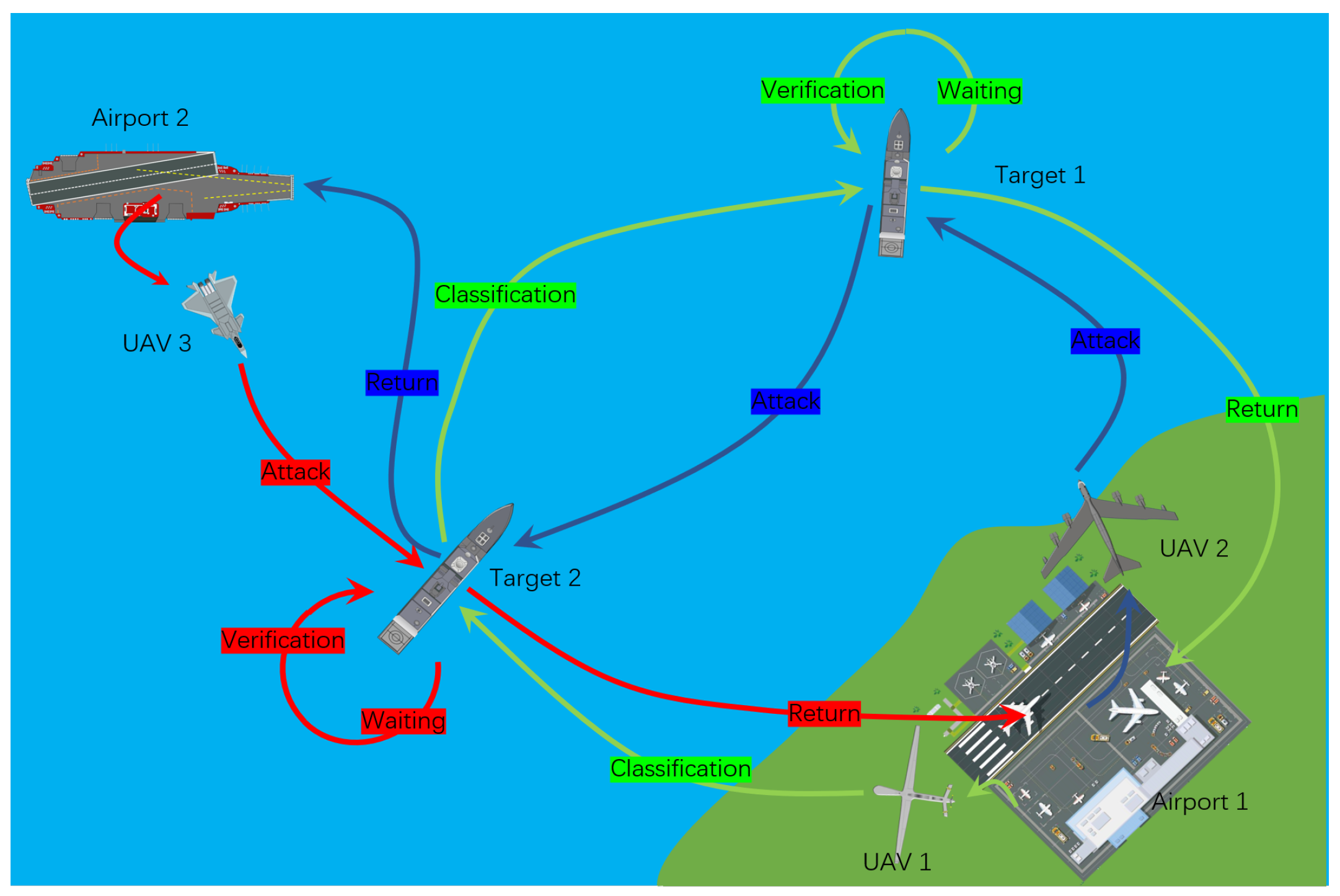
For the above problem description and assumptions,
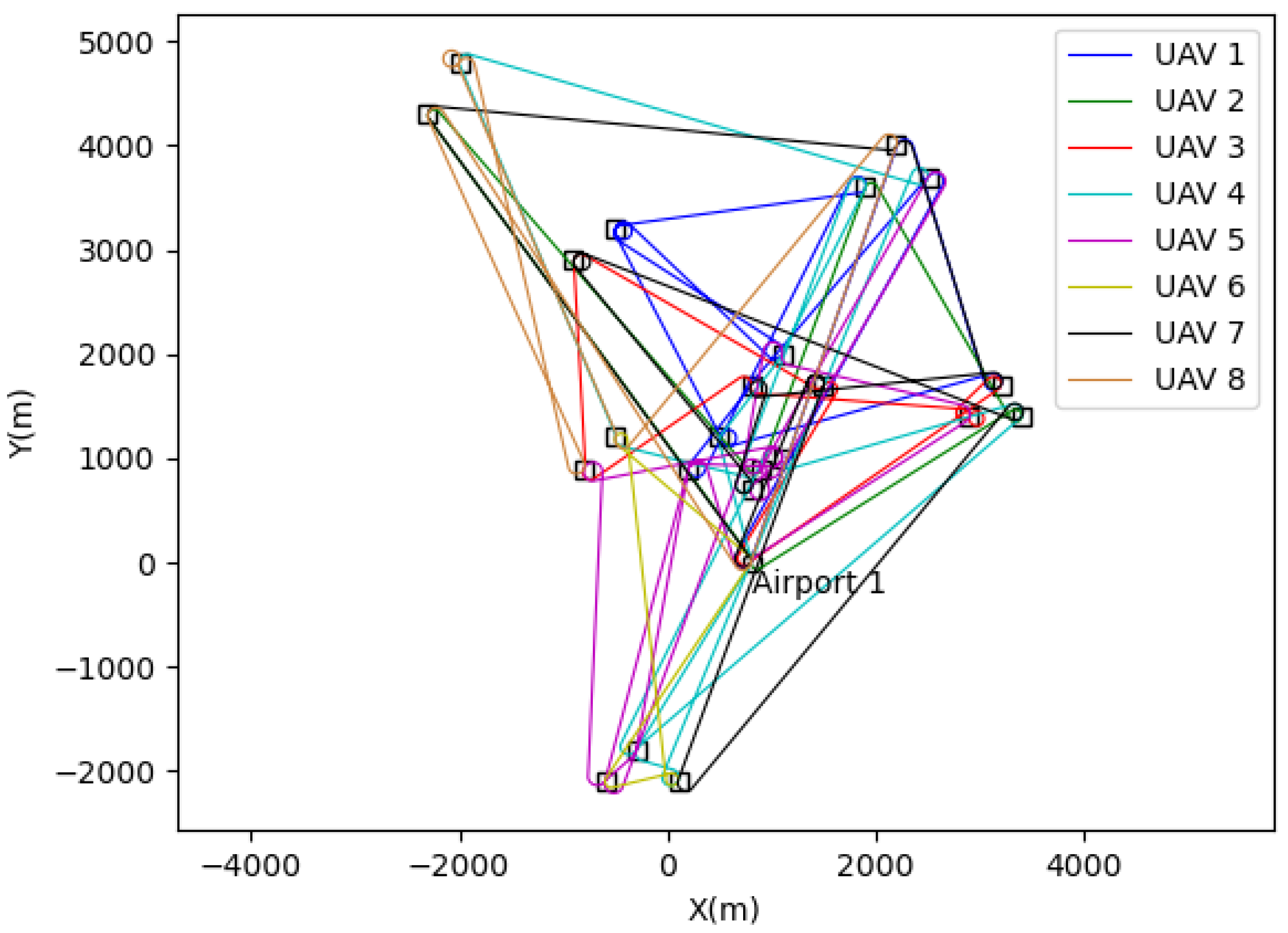
Figure 1 shows an example of cross-regional joint operations for 2 airports, 2 targets and 3 UAVs. Among them,
,
and
are the survival UAV, munition UAV and combat UAV, respectively.
4. An IGA with Flexible Unlock Mechanism
4.1. Chromosome Encoding
According to the above description, in order to make the genetic algorithm suitable for solving the multi-airport task assignment problem, the algorithm needs to be modified. The modified chromosome coding is given in this section.
4.1.1. Encoding Format
In the original genetic algorithm, each chromosome represents a feasible solution. Similarly, this method is also used in the improved algorithm. We know that although the task assignment problem is an NP-hard problem, it is essentially to find the corresponding relationship between tasks and UAVs and the sequence of these corresponding relationships. Therefore, each given plan contains two aspects: 1. the corresponding relationship between UAVs and tasks; 2. the order in which UAVs perform tasks. Based on this idea, the following chromosome fragment can be constructed.
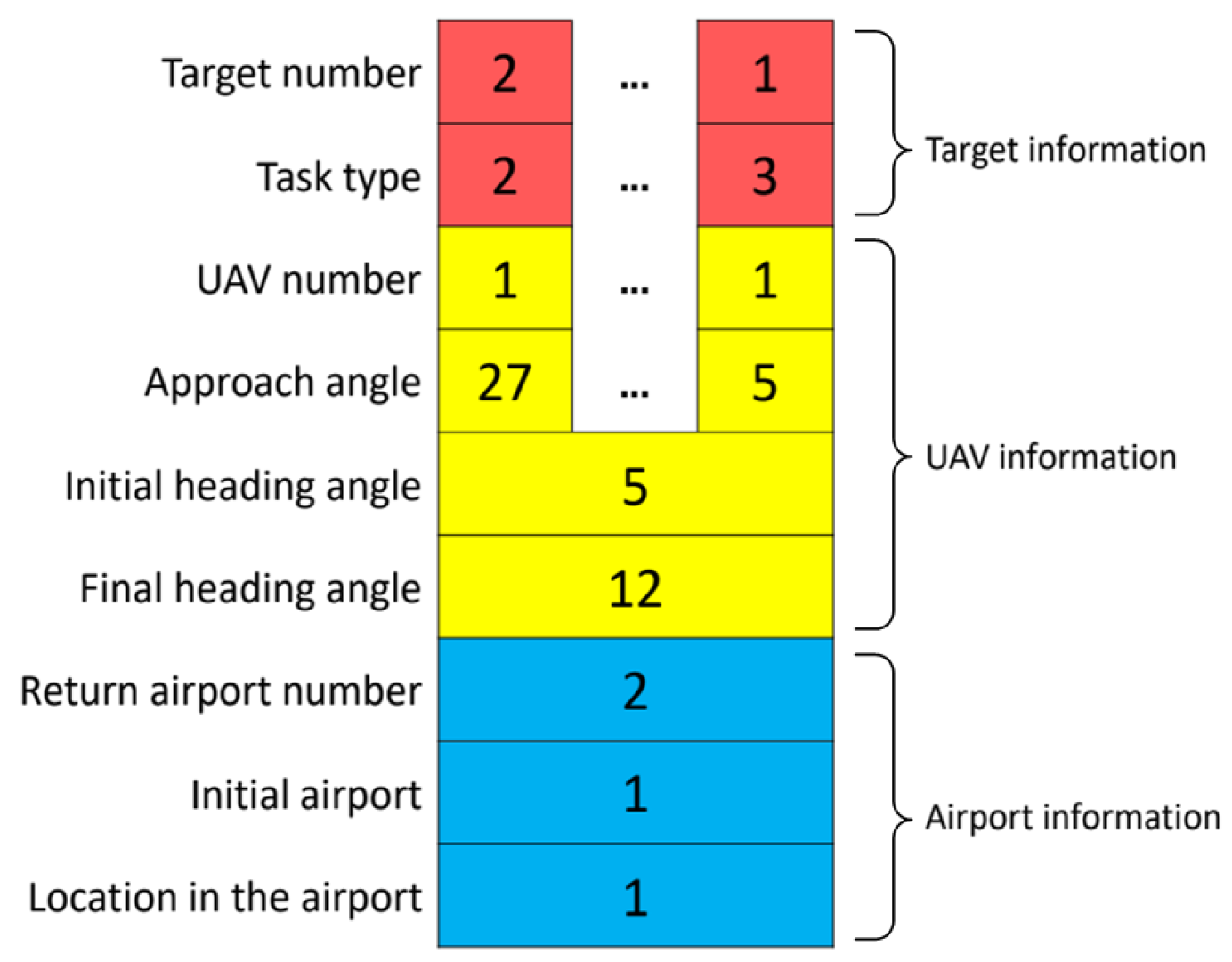
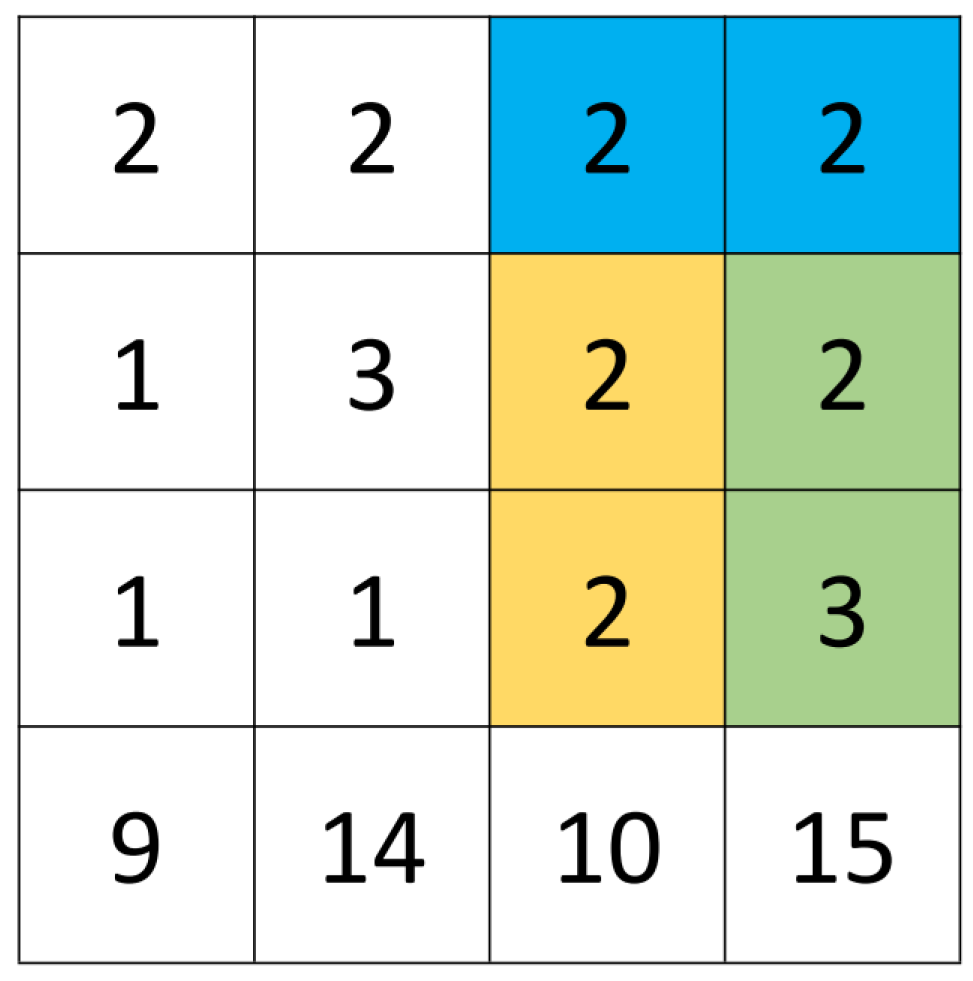
Figure 2 is a chromosome fragment, and the third row represents the number of the UAV.
Figure 2 represents the plan of UAV
in the chromosome. A complete plan is executed by multiple UAVs collaboratively, so a complete chromosome contains several fragments similar to
Figure 1. In addition, in each fragment, the first and second rows are the task number and task type, respectively. The information in the first three rows forms the above-mentioned corresponding relationship between UAVs and tasks. The order of tasks corresponding to the chromosome from left to right is the order of execution of tasks. Because the distance is calculated by using the Dubins path, the information in Dubins path is added to the chromosome. The fourth row is the angle when the UAV approaches the target. The fifth and sixth rows are the angles of the UAV when it leaves and returns to the airport. In addition, the background of multiple airports also makes the chromosome need to include the necessary airport information. The seventh row is the number of the airport where the UAV returns, and the eighth row is the number of the airport where the UAV departs, and the ninth row is the location of the UAV in the airport. For example, in
Figure 2, the eighth and ninth rows in the chromosome indicate that UAV
is at position 1 of airport 1. If UAV
is also at Airport 1, then the values of the eighth and ninth rows corresponding to the UAV
are 1 and 2, respectively. This agreement is to facilitate program calculations.
Figure 3 is a complete chromosome, which consists of several fragments illustrated in
Figure 2.
4.1.2. Initialization Strategy
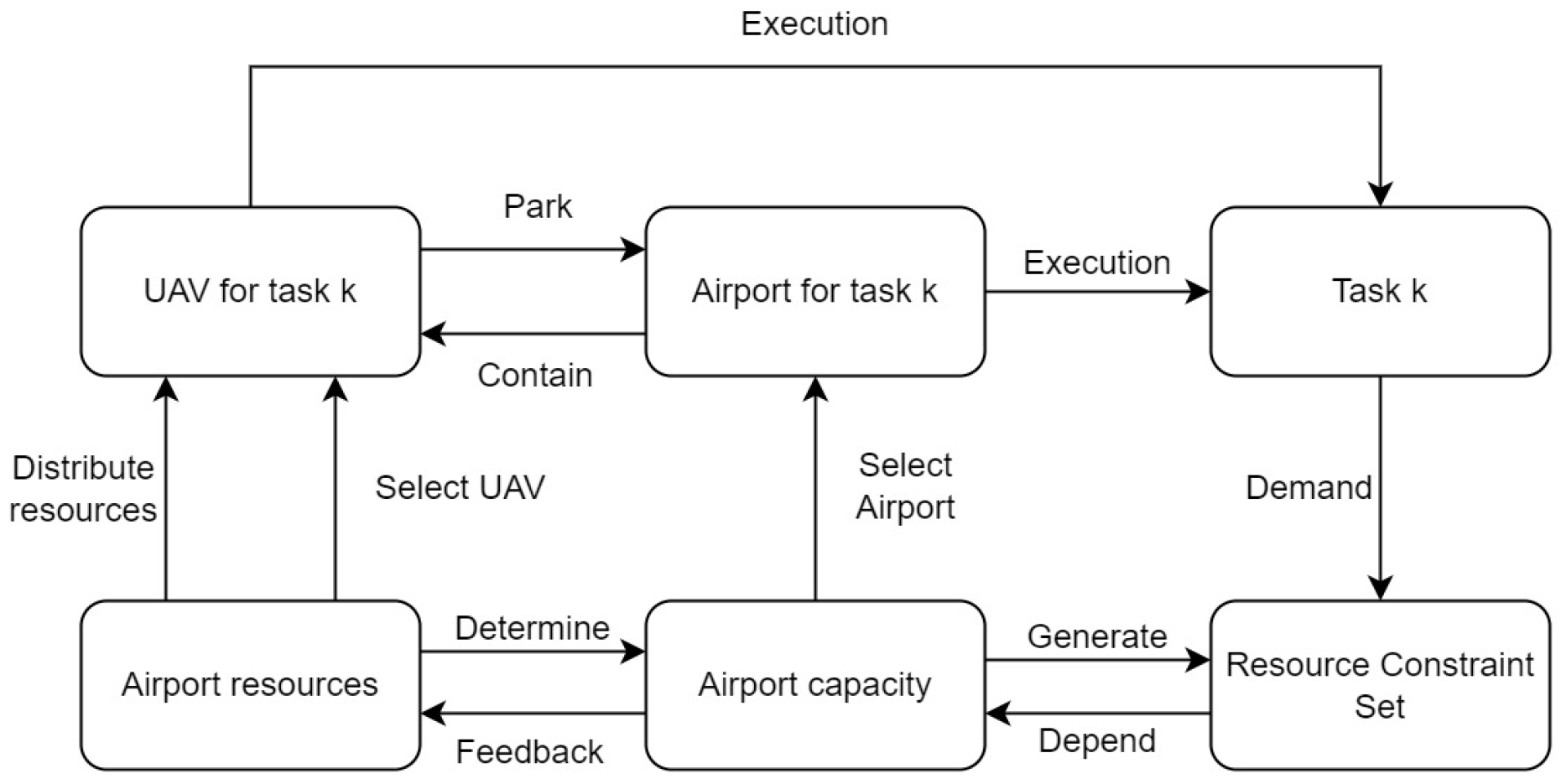
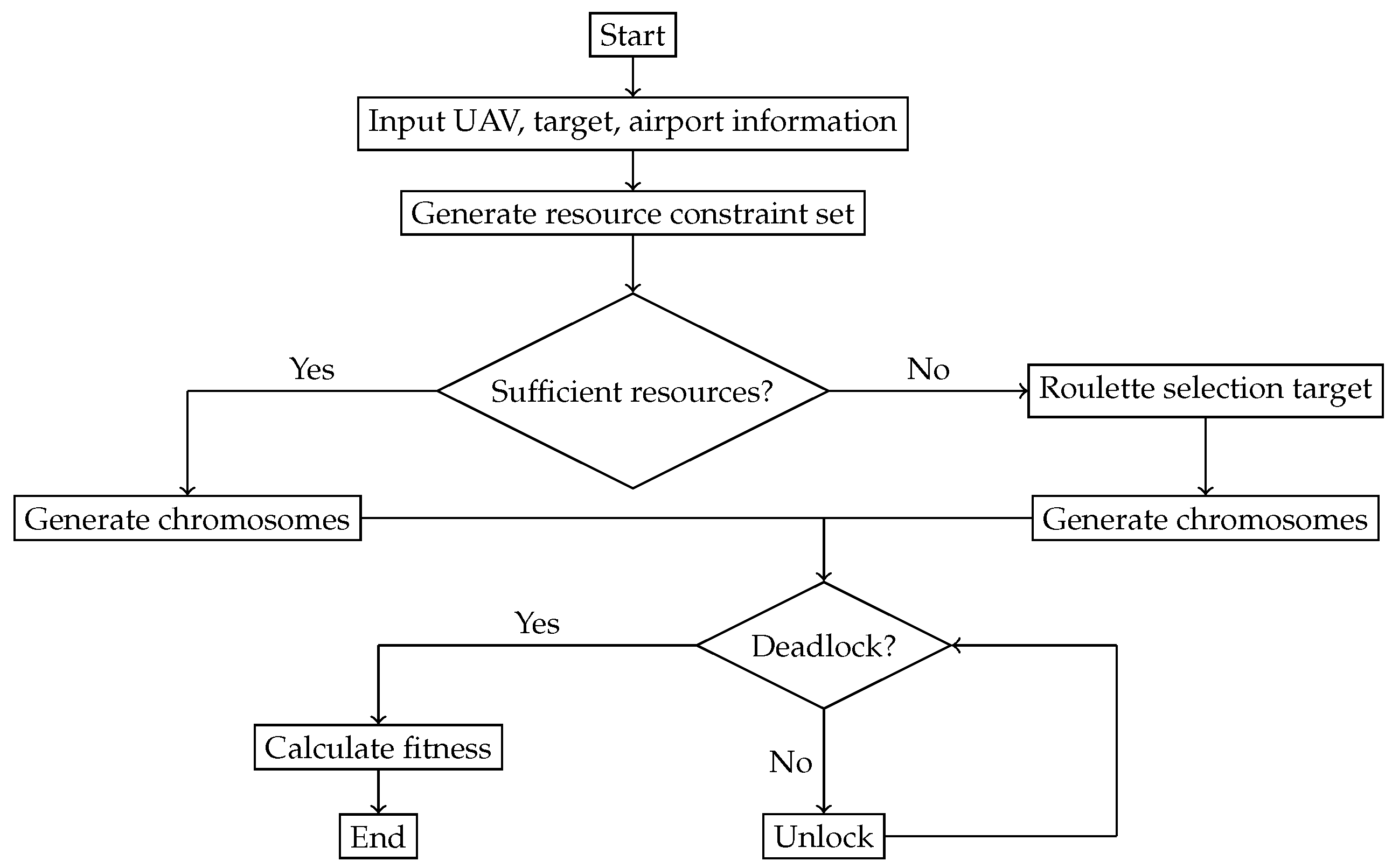
Because the CRJO problem contains many constraints, there are many infeasible solutions in our randomly generated chromosomes, and a large number of infeasible solutions will affect the speed of algorithm convergence. Therefore, in the process of generating chromosomes, we must avoid some infeasible solutions. A resource constraint set is defined in the algorithm of this paper, which is generated according to the ammunition reserves owned by the airport and the docked UAVs, and represents the capabilities of each airport.
Figure 4 shows the process of assigning task k to execute the UAV in the encoding of chromosomes. The advantage of assigning tasks through resource constraint set encoding is that the resulting chromosomes satisfy resource constraints. Therefore, the resource constraint set needs to be used in the subsequent cross-mutation process.
Figure 4 completes the coding of lines 1–3 of the initial chromosome, various heading angles in lines 4–6 are randomly given, and the airport information in lines 7–9 is initially determined. The chromosomes in
Figure 3 are obtained by arranging the generated chromosomes according to the UAV number. Since this article considers the situation of ammunition scarcity, first, we need to judge the size of
and
. If the ammunition is sufficient, assign the UAV to the task of the
targets, otherwise, select
targets by roulette according to the target value, and assign the UAV to perform their tasks.
4.2. Crossover Operator
The crossover operator is an important part of the genetic algorithm. In essence, the crossover operation is to exchange the information of the two chromosomes. This paper, it is to exchange the correspondence between the tasks in the two schemes and the UAV. First, this paper uses the roulette algorithm to select two good parents according to the fitness function value. Second, a single-point crossover method is used to randomly select a point from parent 1 as the crossover starting point. All information from the beginning to the end of parent 1 is exchanged with the corresponding information of parent 2. Since the attack task will involve resource constraints, the crossover of attack information is different from that of classification evaluation.
Furthermore, under the background assumptions of this paper, the number of attacks against the target is no longer deterministic. In the initial process of chromosomes, the number of attacks on the target is 1, but in the subsequent calculation, the algorithm will determine the number of attacks on the target by itself according to the value of the fitness function. Therefore, this will lead to the phenomenon of crossover operation of chromosomes of different sizes during the crossover process, and changes in chromosome dimensions may also occur during the crossover process. The crossover method in this paper takes the dimension of the first chromosome as a reference, so different dimensions and changes in dimensions will not affect the crossover operation.
4.2.1. Crossover of Attack Genes
This section gives the specific operation of single-point crossover of attack genes. Since the attack task involves ammunition constraints, the crossover operation of attack genes will be divided into two cases by discussing whether the attackable UAV set is empty or not. Because the crossover process involves the crossover of chromosomes of different dimensions, the set of attackable UAVs corresponding to one chromosome may be empty, while the other is not. In this case, the chromosome corresponding to the empty set is defined as parent 1. As long as the attackable UAV set of parent 1 is empty, the attackable UAV set is considered empty (the attackable UAV set corresponding to another chromosome may not be empty at this time). We call the constraint that the same target can only be attacked once by the same UAV as constraint A. A detailed description of the single-point crossover of the attack gene is as follows.
If the attackable set is not empty, then the tasks information remain unchanged, and the exchange of the information of the two chromosomes is achieved by exchanging the information of the UAVs performing the attack tasks in the two chromosomes. The specific steps are shown in Algorithm 1, In addition,
Table 1 is a notation description of the algorithm in this section.
A simple example is given to assist readers in understanding the operation flow of the crossover operation when the set of attackable UAVs is not empty. In this example, there are 2 airports, 3 UAVs, and 2 targets. First, two parents are obtained through the roulette algorithm, as shown in the following figure.
| Algorithm 1 Crossover operations where the attackable set is not empty |
Input: , , , Output: , , , - 1:
Find out all the attack tasks of , marked as . - 2:
Remove the UAV number a of the exchange line of from . In addition, let . - 3:
ifthen - 4:
Randomly select an element b from I. - 5:
while b does not satisfy do - 6:
Randomly select an element b from I. - 7:
if a is not in or a does not satisfy then - 8:
Randomly select an element c from . - 9:
- 10:
Change b into the cross column of , and change a into the corresponding column of . - 11:
Update and . - 12:
return, , ,
|
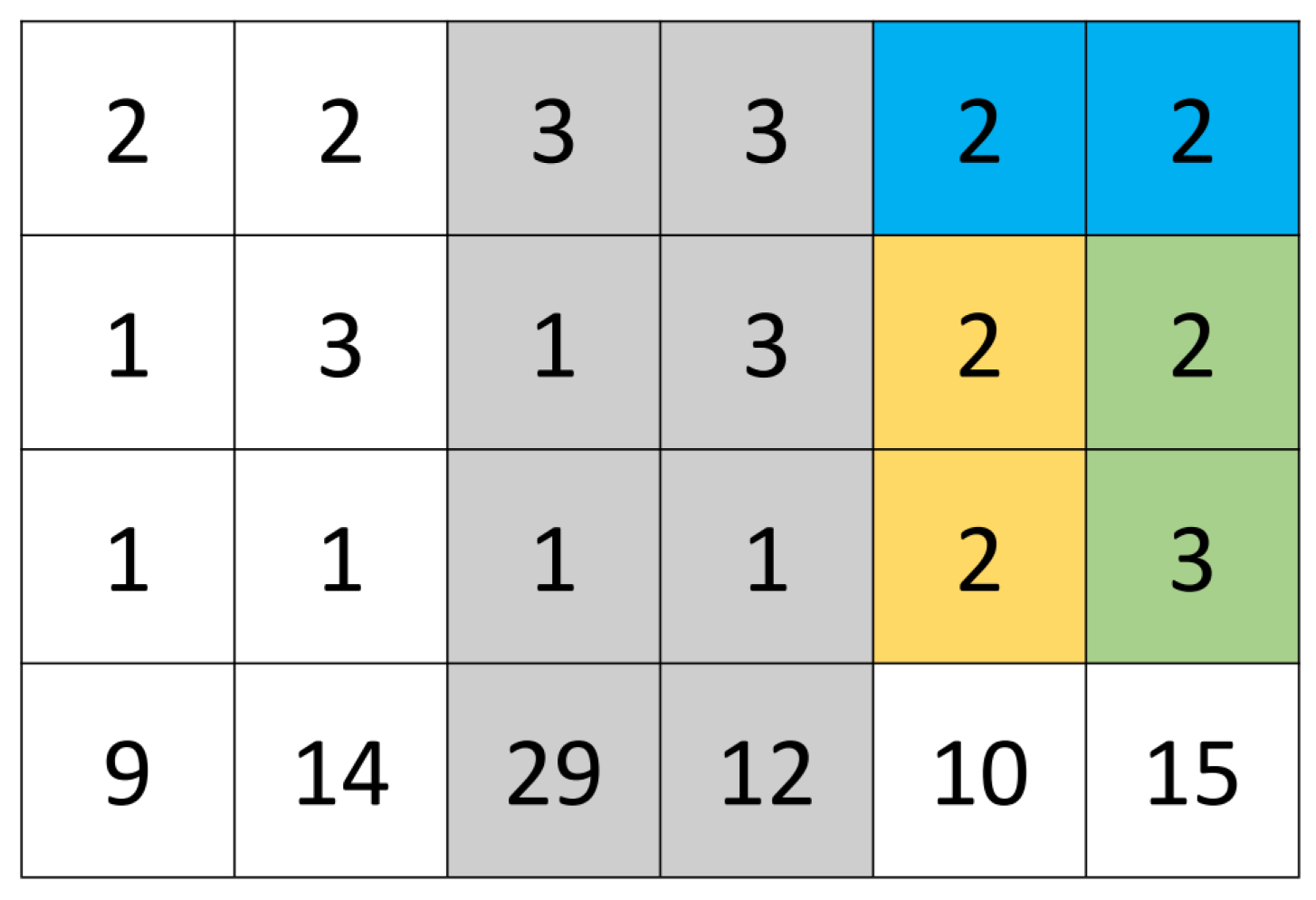
As shown in the
Figure 5, the orange column in parent 1 is the column for single-point crossover operation, and the UAV performing the attack task in this column is
. The attack resource constraint set of parent 1 is
, it means
,
,
that can also perform attack tasks under the task assignment plan of parent 1. The columns of attack tasks in Parent 2 is marked in green in the
Figure 5, and it is represented by a set as
. The attack resource constraint set of parent 2 can also be expressed as
. Remove 2 from
, and then take the intersection with
, which is expressed as
. Because 1 is in
, so the number in the red position of parent 1 can be exchanged with the number in the blue position of parent 2 in the
Figure 5.
After swapping the UAVs of the crossed columns of the two chromosomes, it is also necessary to swap the approach angle and other information, and finally get the result shown in the
Figure 6. This is the process of single-point crossover operation of attack genes when resources are sufficient.
When the attackable set is empty, then all the ammunition are allocated, so the operation of changing the UAV cannot be performed. According to the previous description, the nature of crossover operation is to exchange the corresponding relationship between the targets and the UAVs in the two chromosomes. Therefore, when the attack set is empty, the UAVs that perform the attack task can be fixed, and the targets being attacked in the two parents can be exchanged.
Table 1 is a notation description of the algorithm in this section. If
is not an empty set, when the crossover operation is performed on chromosome 1 and chromosome 2, chromosome 1 can refer to the information of chromosome 2 for internal exchange. Internal exchange is a random selection of an element of
, which is a target that the UAV
did not perform on chromosome 1, but according to the definition of the set, this target is chromosome 2 The target of the attack mission performed by
. Exchange this target with the target executed by
in chromosome 1, so as to indirectly achieve the purpose of exchanging information with chromosome 2. Similarly, if
is not an empty set, chromosome 2 can also refer to the information of chromosome 1 for internal exchange. We refer to the restriction of internal exchange as Constraint B.
The specific steps are shown in Algorithm 2.
| Algorithm 2 Crossover operations where the attack set is empty |
Input: , , Output: , - 1:
Calculate ,,, according to , . - 2:
ifthen - 3:
Calculate ,. - 4:
- 5:
while do - 6:
if and then - 7:
Randomly select an element a from , elect an element b from . - 8:
if a, b satisfies then - 9:
and are exchanged internally accordingly. - 10:
- 11:
else - 12:
Remove the corresponding elements from ,. - 13:
if and then - 14:
Randomly select an element a from . - 15:
if a satisfies then - 16:
exchanges internally. - 17:
Replace cross column elements into , and adjust . - 18:
- 19:
else - 20:
Remove a from . - 21:
if and then - 22:
Randomly select an element b from . - 23:
Traverse if can be exchanged internally, record ; - 24:
if then - 25:
exchanges internally. - 26:
Replace cross column elements into , and adjust . - 27:
- 28:
else - 29:
Remove the corresponding elements from . - 30:
if and then - 31:
Replace cross column elements into , and adjust . - 32:
Replace cross column elements into , and adjust . - 33:
- 34:
return,
|
In order to facilitate readers to understand the above-mentioned crossover process, take the situation that resources are insufficient as an example to illustrate how the crossover operation is performed. The example contains 2 airports, 4 targets, 3 UAVs, and each airport has 1 ammunition. The two parents are given as follows:
The orange column of parent 1 in the
Figure 7 is the column where parent 1 performs single-point crossover operation, and the target number that needs to be changed is marked in red. Obviously,
,
,
,
,
,
. The UAV that performs the attack task in the crossed column of parent 1 is
. In parent 2, we also use orange to mark the column that
performs the attack task, and the target number is marked in blue. As shown in the
Figure 7, there is only one column for
to execute the attack, so this column can only be used as the crossed column of parent 2. If there are multiple columns of
to perform the attack task in Parent 2, it is necessary to use the information of
,
to select the crossed columns according to the algorithm steps. In this example,
is not empty, so first determine whether parent 1 can be exchanged internally. We mark the column in parent 1 that performs attack tasks on target 1 in green, and the target is marked in blue. We found that the numbers in the red block and the blue block in parent 1 can still satisfy the constraints after being exchanged, so parent 1 can be exchanged internally. Since
is an empty set, the number 3 can only be exchanged into the blue block of parent 2 to replace the previous number 1. After this treatment, there are no attack tasks of target 1 in parent 2, so the classification task and verification task (the gray column in parent 2) are meaningless, so they need to be deleted in the subsequent operations.
The result obtained after the two chromosomes are crossed is shown in the
Figure 8. The target 1 and target 3 in parent 1 are interchanged. Change the previous target 1 in parent 2 to target 3, because there was no attack task of target 3 in the previous chromosome, so after adding the attack task of target 3, the classification task and verification task of target 3 are need to be added, such as the red columns in parent 2. The above process completes the single-point crossover operation for the attack task in the case of insufficient resources.
4.2.2. Crossover Operations of the Classification Genes and the Verification Genes and the Heading Angles
Because the ammunition constraints do not need to be considered in the classification and verification tasks, so their crossover method is simple. The crossover operation is similar to the simplified version of the crossover operation where the attackable set is not empty. The specific steps are shown in Algorithm 3.
| Algorithm 3 Crossover operator for classification and verification tasks |
Input: , , , Output: , , , - 1:
Find all UAVs that perform classification and verification tasks in , marked as . - 2:
Remove the UAV number a of the exchange line of from . In addition, let . - 3:
ifthen - 4:
Randomly select an element b from I. - 5:
Change b into the cross column of , and change a into the corresponding column of . - 6:
Update and . - 7:
return, , ,
|
In addition, in the fifth step of the crossover operation, the initial and final heading angles of the two chromosomes need to be exchanged.The specific steps are shown in Algorithm 4.
| Algorithm 4 The heading angle crossover operator |
Input: , Output: , - 1:
Count the number of heading angles of and and record them as and , respectively. - 2:
. - 3:
. - 4:
Exchange the first R heading angles of and . - 5:
return,
|
The above is all about performing crossover operations on a pair of chromosomes.
4.3. Mutation Operator
In this paper, mutation operation can not only prevent the algorithm from falling into a local optimum, but also change the dimension of chromosomes by adding or deleting attack tasks for a certain target. The mutation operation mainly consists of two parts. The probability of the occurrence of a given mutation. When the generated random number is less than , perform related operations. First of all, to make the attack times of each solution to the target not fixed, it is necessary to increase or decrease the attack times of a certain target during the mutation process. Second, to avoid falling into a local optimum, it is necessary to change the task sequence of the random UAVs in the scheme and the various heading angles of the randomly selected UAVs.
We want to increase the number of attacks on high-value targets when each target has value. In addition, we want to drop low value targets when ammo is limited. For the selection method of high-value targets, the value of the target is used as the standard, and high-value targets are selected through roulette. In the case of insufficient resources, repeated attacks on some high-value targets meant that some low-value targets had to be abandoned. This paper takes the inverse of the target value and selects low-value targets through the roulette method. The Algorithm 5 gives the algorithm flow for the first part of the mutation.
We call the constraint A that the same UAV can only attack the same target once and the total number of attacks . In addition, we call the attack task whose resource constraint set can guarantee the increase of the corresponding target as constraint C.
In order to facilitate the readers to understand the above process, a simple example is given here. The example contains 2 airports, 4 targets, 3 UAVs, and each airport has 1 ammunition. This example is used to illustrate how the algorithm can increase the number of attacks on a certain target when resources are insufficient. The initial chromosome for the mutation operation is given in
Figure 9.
| Algorithm 5 Mutation operations |
Input: , , Output: c, - 1:
- 2:
whiledo - 3:
Roulette chooses a target a that increases the number of attacks. - 4:
if a satisfies . then - 5:
if a satisfies . then - 6:
Increase the number of attacks on a. - 7:
- 8:
else - 9:
- 10:
while do - 11:
Copy c and as and . - 12:
Delete an attack task of and update . - 13:
if a and satisfies . then - 14:
- 15:
,. - 16:
Increase the number of attacks on a. - 17:
- 18:
Update the heading angle of c. - 19:
returnc,
|
First, the roulette method is used to select the target that needs to be increased the number of attacks. Since target 2 has the highest value, it has the greatest probability of being selected. In this example, the target that needs to be increased the number of attacks is also target 2. The second step of the algorithm needs to determine whether the target 2 can be attacked again. Although target 2 has been attacked once in the chromosome, there are two UAVs that can perform the attack task, so in theory, target 2 can still be attacked again. Because the current resource constraint set is empty, the target of some attack tasks in the chromosome needs to be replaced with target 2. Because in the chromosome, except for the orange column, only the green column is the attack task column. Therefore, replace the value in the gray position in the
Figure 9 with 2. When the value of the gray position is changed to 2, the chromosome still satisfies the constraint, so this operation is reasonable.
After the replacement, the attack task of target 3 does not exist in the chromosome, so the classification task and verification task of target 3 are meaningless (the column marked in gray in the
Figure 10). The original chromosome contains the classification task and verification task for target 2, so there is no need to add the classification task and verification task for target 2 after replacement.
The
Figure 11 is the final result of the mutation operation. The size of the chromosome has been changed through the mutation operation.
4.4. Program Initialization
The content of chromosome initialization coding has been described in detail above. At the same time, a very important part of program initialization is the calculation of fitness. Many issues in fitness calculation will be discussed in this part.
4.4.1. Unlock
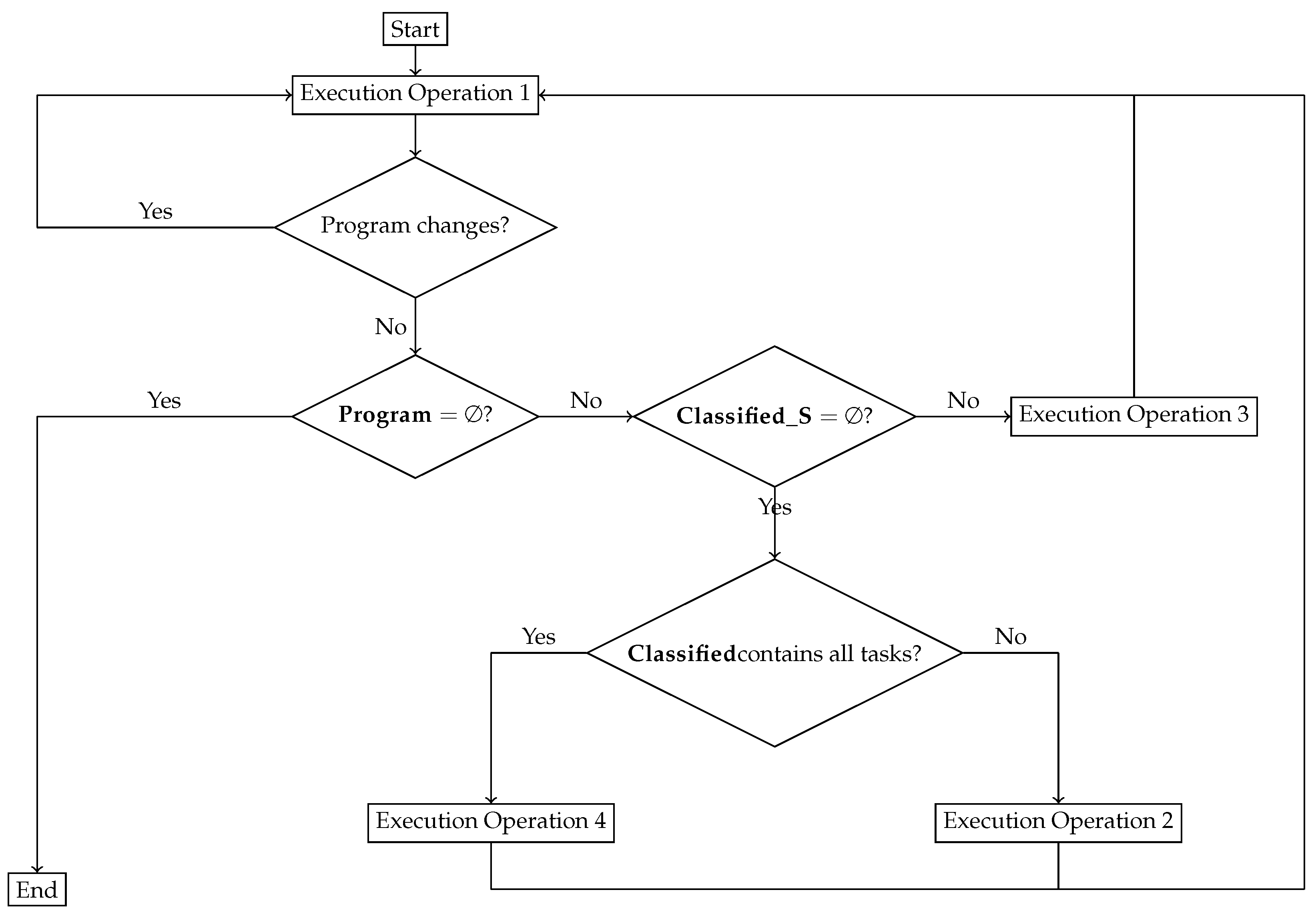
This article uses a logic-based unlocking method to deal with the deadlock issue. This unlocking method can extract the program information contained in the chromosome, and then logically determine whether it is locked and use corresponding strategies for different deadlock scenarios.
First, we define some set symbols as shown in
Table 2. Through the previous explanation of the structure of the chromosome, we know that a chromosome represents a task assignment plan. Each UAV executes a part of the overall plan. We call the part executed by UAV
as a sub-program (Subprogram) of the overall plan. Next, we define the Subprogram task execution logic and four strategies.
Task execution logic: we traverse the program of the UAV .
1. When encountering a reconnaissance task, we remove the task from the Subprogram, and then add it to and .
2. When encountering an attack task, we judge whether the target number is in , if it is in it, execute the attack task, and remove the task from the Subprogram, and update , add 1 to the number of attacks on the target. At this time, if the number of attacks on the target is equal to the total number of attacks in the plan, the target number is added to and removed from .
3. When encountering an evaluation task, we judge whether the target is in , if it is, we remove the task from the Subprogram, and add the target number to .
Operation 1. Use task execution logic for each Subprogram in the overall program.
Operation 2. Traverse each Subprogram to find the reconnaissance task, and if found, exchange the execution order with the first task of the current Subprogram, and use task execution logic for the Subprogram of the exchange order.
Operation 3. Find the attack task of the first element in , and if found, exchange the execution order with the first task of the current Subprogram, and use the task execution logic for the Subprogram of the exchange order and the subsequent Subprograms.
Operation 4. Traverse , Find the first attack mission of the target that did not complete the attack mission. The found target exchanges the execution order with the first task of the current sub-program. And use task execution logic for the sub-schemes of the exchange sequence.
After defining the above four strategies, We combine them through the process in
Figure 12 to get a logic-based unlocking method.
4.4.2. Fitness Function and Initialization
In the program initialization process, we first calculate the optimal solution in the initial population, and use of this optimal solution as the initial value of and as the initial value of . In the optimization process, and are constantly changing and the magnitude of the change is not the same, which will actually change the fitness function. In order to ensure that the actual meaning of the fitness function does not change significantly during the iteration process, we need to iterate a certain number of times to update the standard value. Every time the specified number of iterations is reached, the standard value is replaced with and of the optimal solution of this generation.
Here is a special explanation that constantly changing the
for dimensionlessness will not affect the optimization process. In other words, constantly changing the dimensionless dividend
can still ensure that the algorithm is moving towards to the optimal direction. For example, we suppose
. In the first dimensionless process, we choose
a as the
, compare
, we can see that
is smaller. Selecting
c as the
for the second time, comparing
, obviously
f is the smallest, when a is the dividend,
f is also the smallest. After adding a minus sign to all values, the maximum value of this group of numbers becomes
. Taking f as the first
, through similar discussions, we can also know that updating
will not affect the optimization. In summary, the constant replacement of
can still ensure that the algorithm proceeds in the direction of optimization.
Section 5.3 will discuss the impact of the replacement frequency of
on the two optimization indicators.
In the actual calculation process, the value of the fitness function of Formula (
4) theoretically should be [−1,1], and the roulette in the algorithm requires the value of the fitness function to be of the same sign. So we shift the fitness function value by one unit and turn it into a number between [0,2]. Finally, the fitness function will eventually become
The overall process of initialization is shown in
Figure 13.