Research on Modeling and Fault-Tolerant Control of Distributed Electric Propulsion Aircraft
Abstract
:1. Introduction
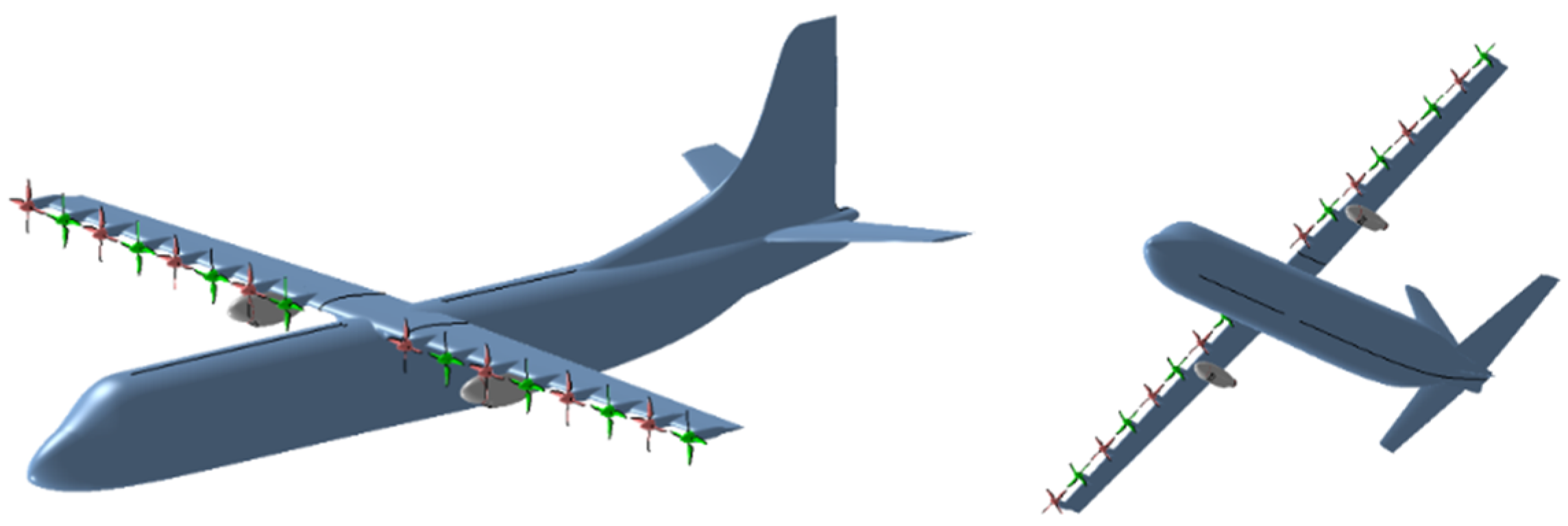
2. Modelling of the DEP Aircraft
2.1. Mathematical Model of the DEP Aircraft’s Propulsion System
2.1.1. Engine Module
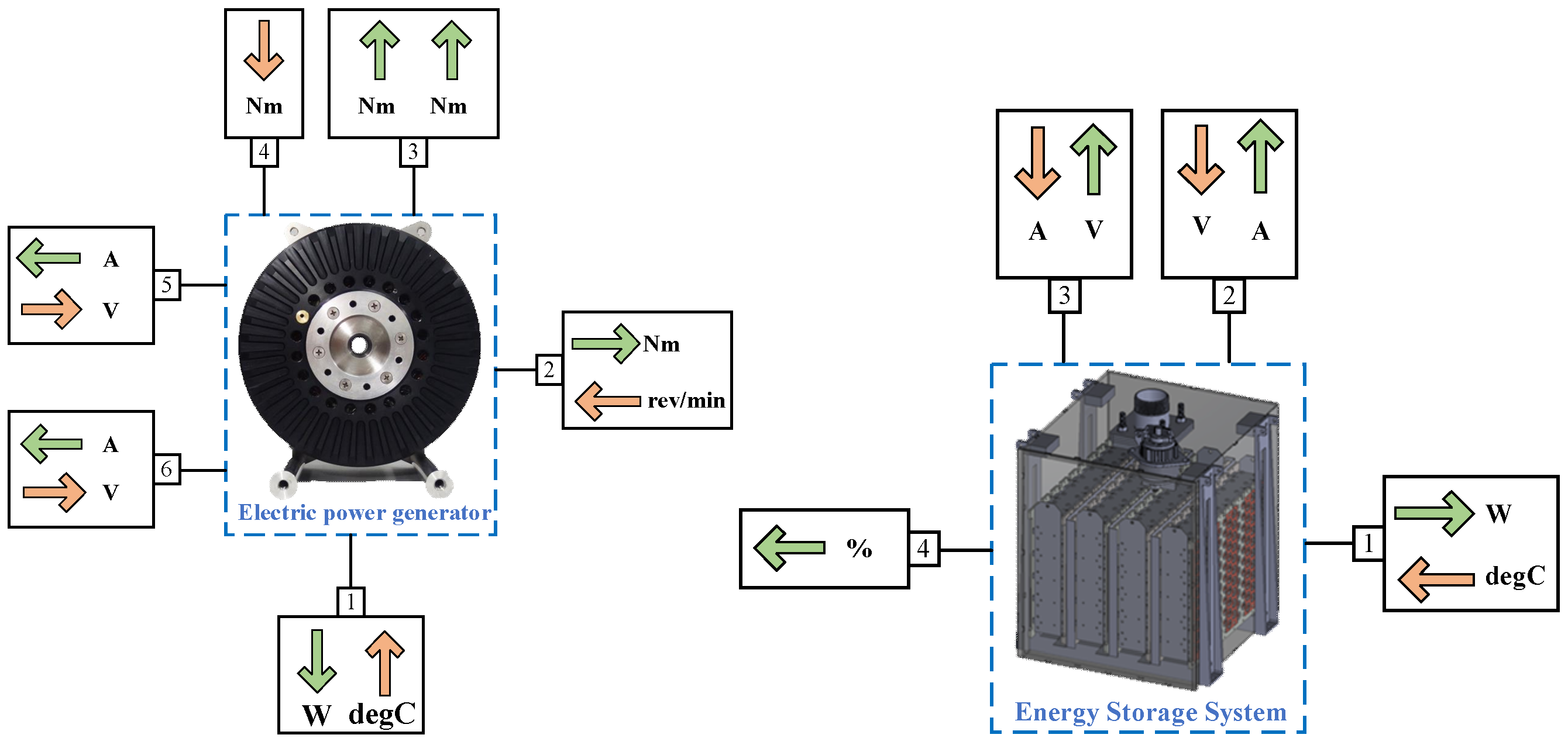
2.1.2. Electric Power Generation and Energy Storage Module
2.1.3. Thruster Module
2.2. Mathematical Model of the DEP Aircraft
2.2.1. Earth-Surface Reference Frame
2.2.2. Aircraft-Body Coordinate Frame
2.2.3. Velocity of Aircraft Relative to the Air
2.2.4. Angle of Attach and Sideslip Angle
2.2.5. Force and Moment
2.2.6. Flight Dynamics Equations
3. Coordinated Thrust Control and Fault-Tolerant Control of the DEP Aircraft
3.1. Coordinated Thrust Control of the DEP Aircraft
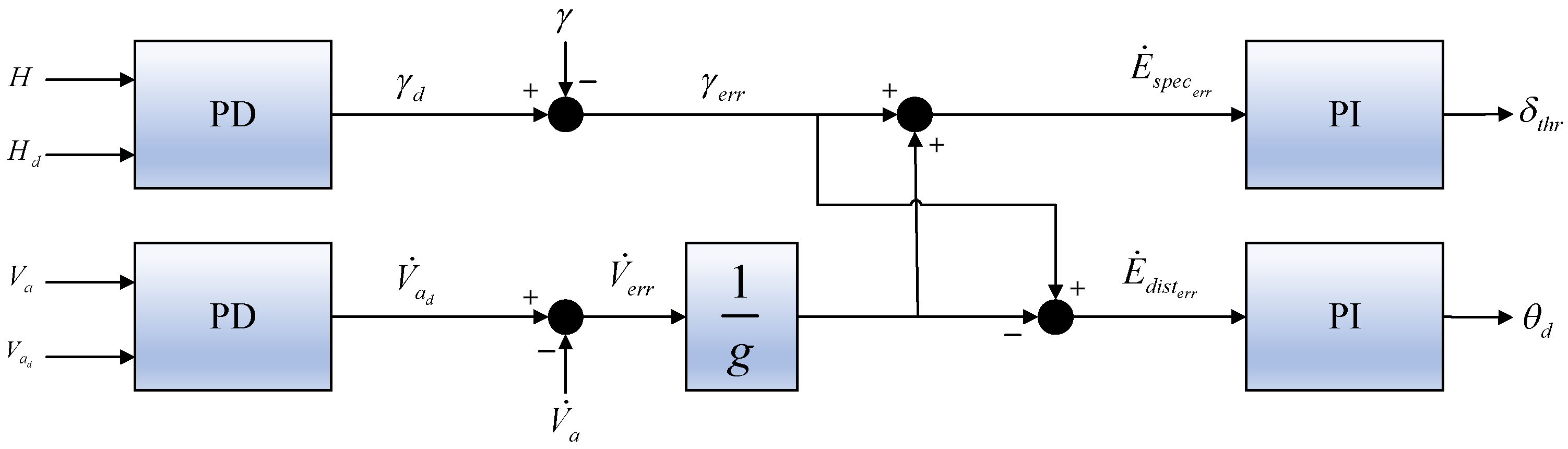
3.1.1. Longitudinal Control Loop
3.1.2. Lateral Control Loop
3.2. Fault Response Strategy and Fault-Tolerant Control of DEP Aircrafts
4. Simulation Results and Discussion
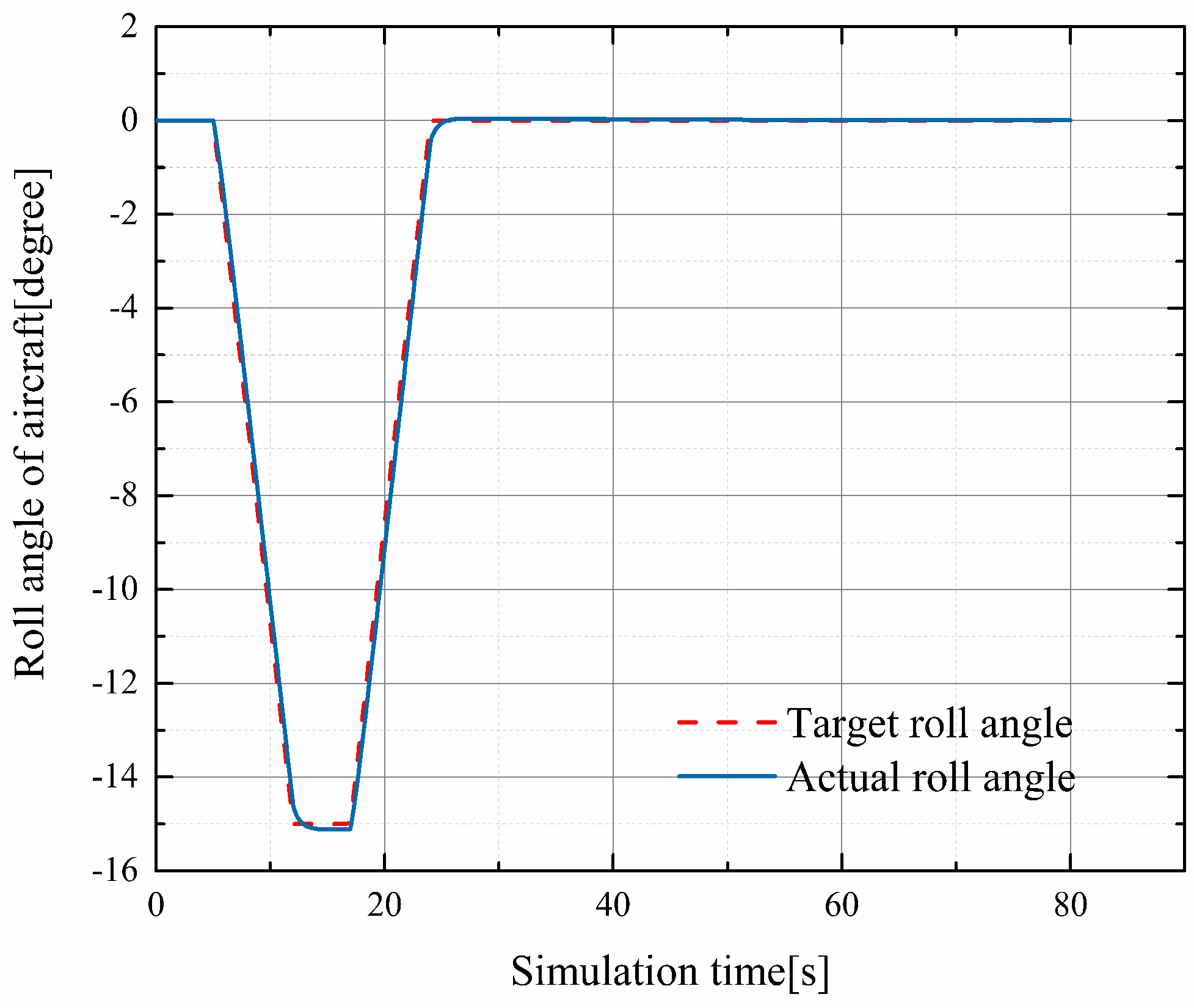
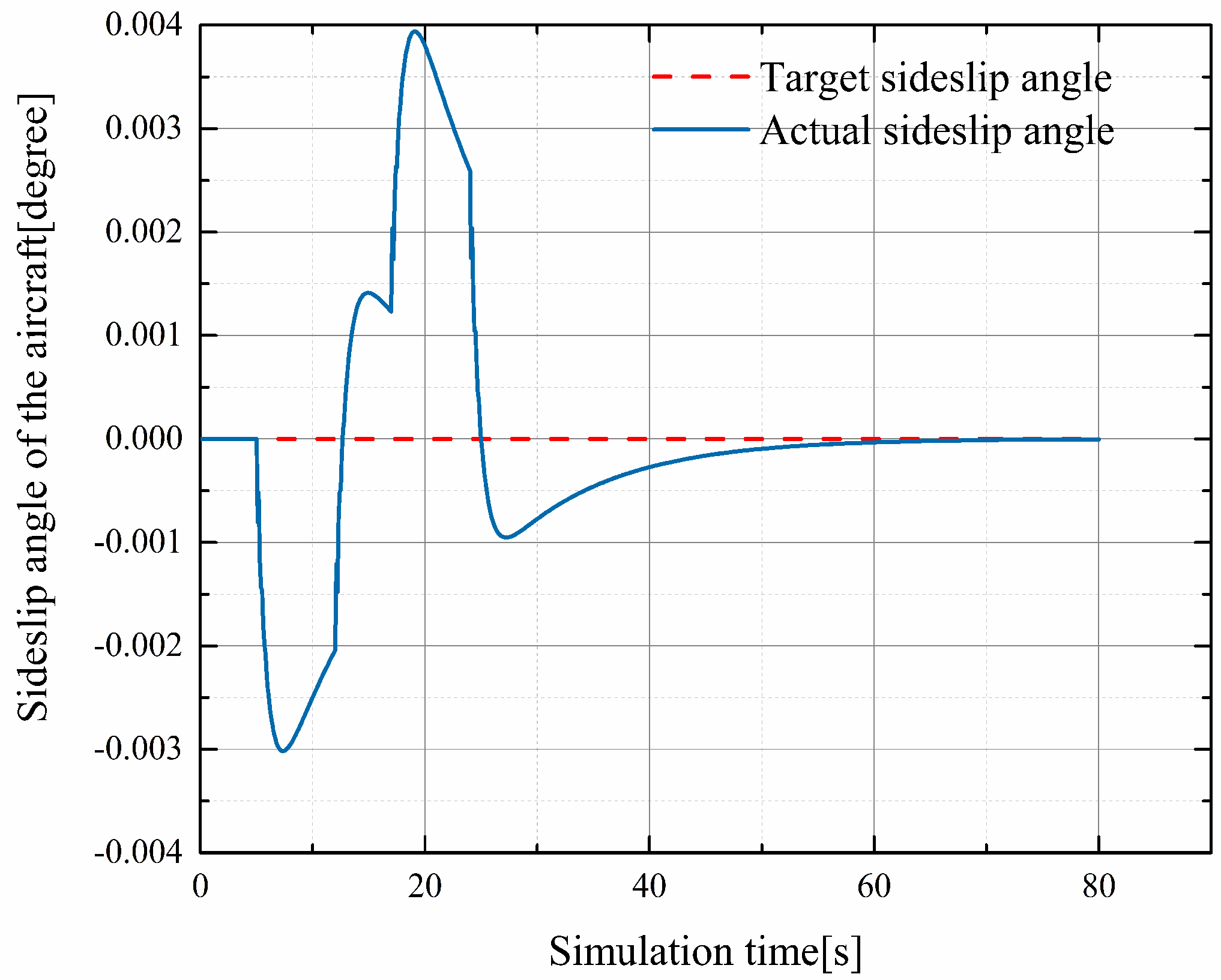
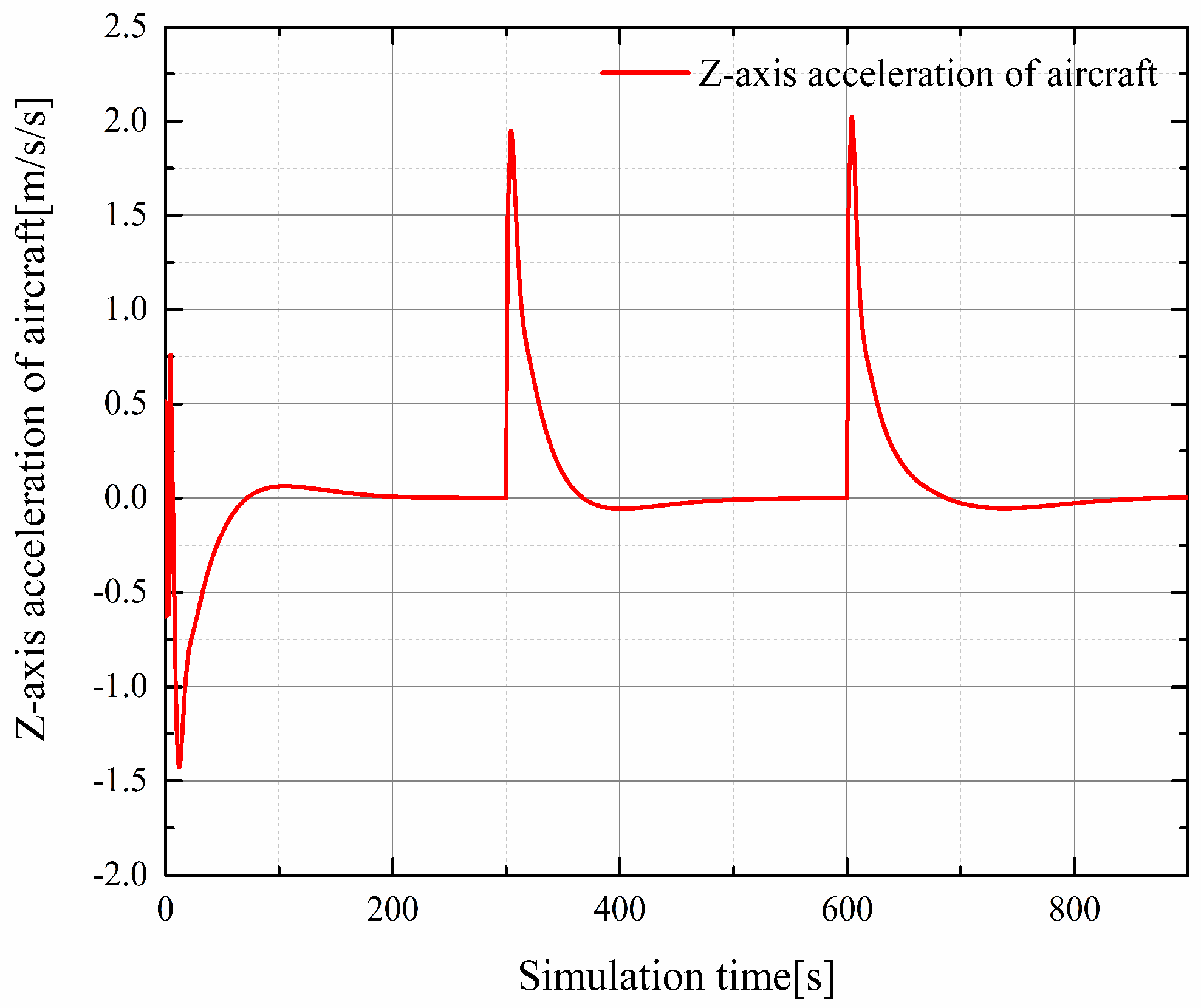
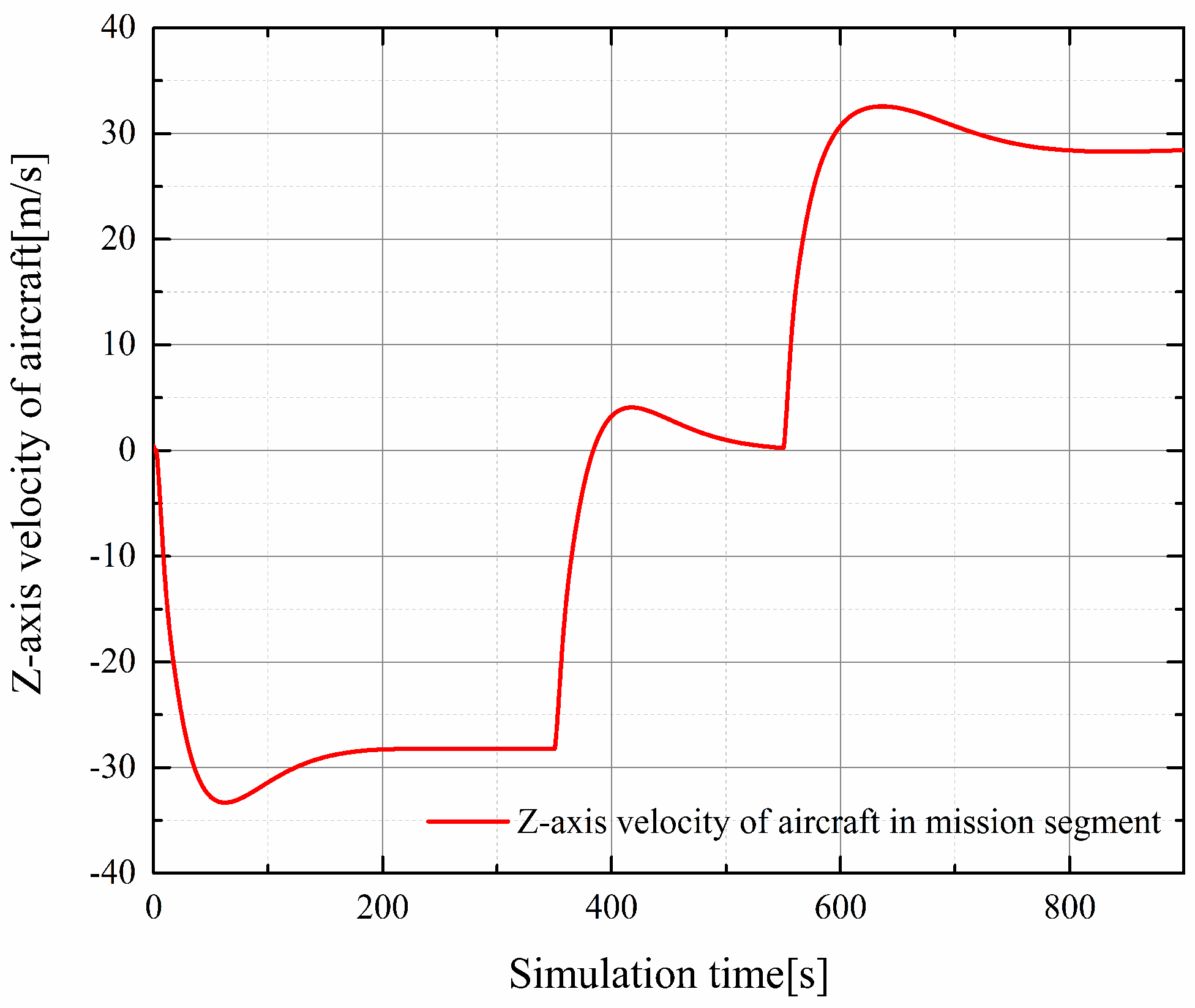
4.1. Simulation Tests Carried out within Mission Segments
4.2. DEP System Thruster Fault-Tolerant Control Simulation Test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | ||
| DEP | distributed electric propulsion | |
| NASA | National Aeronautics and Space Administration | |
| TeDP | turboelectric distributed propulsion | |
| VTOL | vertical takeoff and landing | |
| TIT | turbine inlet temperature | |
| SOC | state of charge | |
| Roman letters | ||
| specific heat ratio of the ideal gas | ||
| total pressure | ||
| total temperature | ||
| static pressure | ||
| static temperature | ||
| Mach number | ||
| total inlet pressure of compressor | ||
| total outlet pressure of compressor | ||
| total inlet temperature of compressor | ||
| total outlet temperature of compressor | ||
| constant pressure specific heat | ||
| total inlet temperature of gas turbine | ||
| total inlet temperature of power turbine | ||
| total inlet pressure of gas turbine | ||
| total inlet pressure of power turbine | ||
| total inlet pressure of nozzle | ||
| total outlet pressure of nozzle | ||
| mass flow of air | ||
| heat exchanged with the system | ||
| mass flow of fuel | ||
| maximum mass flow of fuel | ||
| heat value of fuel | ||
| highest temperature of the turbine inlet temperature | ||
| power recovery of the turboshaft engine | ||
| specific fuel consumption | ||
| mechanical power of the generator | ||
| torque of the shaft at the generator’s Port 2 | ||
| rotational speed of the shaft at the generator’s Port 2 | ||
| lost power | ||
| electrical energy generated by generator | ||
| load of the charge extracted from the energy storage system for use | ||
| current of a battery at Port 3 of the energy storage system | ||
| rated capacity of a battery | ||
| output power of the energy storage system at Port 1 | ||
| internal resistance of a battery cell | ||
| battery current | ||
| number of cells in series in a battery | ||
| number of cells in parallel in a battery | ||
| thrust of a single propeller | ||
| torque of a single propeller | ||
| thrust coefficient of a single propeller | ||
| power coefficient of a single propeller | ||
| rotational speed | ||
| diameter of propeller | ||
| propulsion ratio of the propeller | ||
| airspeed vector | ||
| norm of the airspeed vector | ||
| linear velocity of the aircraft’s x-axis | ||
| linear velocity of the aircraft’s y-axis | ||
| linear velocity of the aircraft’s z-axis | ||
| angular velocity of the aircraft’s x-axis | ||
| angular velocity of the aircraft’s y-axis | ||
| angular velocity of the aircraft’s z-axis | ||
| Earth-surface reference frame | ||
| aircraft-body coordinate frame | ||
| relative velocities to the Earth | ||
| relative wind speed to the Earth | ||
| mass of aircraft | ||
| wing area | ||
| wingspan | ||
| mean aerodynamic wing chord | ||
| drag coefficient | ||
| lateral force coefficient | ||
| lift coefficient | ||
| roll moment coefficient | ||
| pitch moment coefficient | ||
| yaw moment coefficient | ||
| moment of inertia of the aircraft | ||
| total energy of the aircraft | ||
| kinetic energy of the aircraft | ||
| potential energy of aircraft | ||
| altitude of the aircraft | ||
| gravitational acceleration | ||
| proportional gain of thrust control loop | ||
| integral gain of thrust control loop | ||
| specific energy distribution rate | ||
| incremental thrust | ||
| specific energy gradient | ||
| commanded pitch angle changes | ||
| proportional gain of pitch angle control loop | ||
| integral gain of pitch control loop | ||
| change of elevator deflection angle | ||
| combined thrust control and function | ||
| combined pitch control and elevator actuator dynamics function | ||
| commanded roll angle changes | ||
| commanded yaw rate changes | ||
| proportional gain of roll angle control loop | ||
| integral gain of roll angle control loop | ||
| proportional gain of yaw rate control loop | ||
| integral gain of yaw rate control loop | ||
| ailerons controller and the actuator dynamics function | ||
| rudder controller and the actuator dynamics function | ||
| state matrices of the thrusters | ||
| total yaw moment provided by DEP system | ||
| random fault thruster ID number | ||
| Greek letters | ||
| specific heat ratio of the ideal gas | ||
| efficiency defined by the motor’s characteristics | ||
| air density | ||
| rotational speed in the international system of units | ||
| propeller’s aerodynamic efficiency | ||
| roll angle of the aircraft | ||
| pitch angle of the aircraft | ||
| yaw angle of the aircraft | ||
| angle of attack | ||
| sideslip angle | ||
| track angle | ||
| fault rate | ||
| time of thruster failure in simulation | ||
| control error of yaw angle | ||
| Subscript | ||
| vector component corresponding to the x-axis of the coordinate system | ||
| vector component corresponding to the y-axis of the coordinate system | ||
| vector component corresponding to the z-axis of the coordinate system | ||
| the variable control command input into the system | ||
| thruster’s variable on the left side of DEP aircraft | ||
| thruster’s variable on the right side of DEP aircraft | ||
| count value of left thruster | ||
| count value of right thruster | ||
| Superscript | ||
| vector or scalar under the aircraft-body coordinate frame | ||
| vector or scalar under the Earth-surface reference frame | ||
| Prefix | ||
| change value of variable | ||
References
- Serrano, J.R.; García-Cuevas, L.M.; Bares, P.; Varela, P. Propeller Position Effects over the Pressure and Friction Coefficients over the Wing of an UAV with Distributed Electric Propulsion: A Proper Orthogonal Decomposition Analysis. Drones 2022, 6, 38. [Google Scholar] [CrossRef]
- Amoozgar, M.; Friswell, M.; Fazelzadeh, S.; Khodaparast, H.H.; Mazidi, A.; Cooper, J. Aeroelastic Stability Analysis of Electric Aircraft Wings with Distributed Electric Propulsors. Aerospace 2021, 8, 100. [Google Scholar] [CrossRef]
- Serrano, J.; Tiseira, A.; García-Cuevas, L.; Varela, P. Computational Study of the Propeller Position Effects in Wing-Mounted, Distributed Electric Propulsion with Boundary Layer Ingestion in a 25 kg Remotely Piloted Aircraft. Drones 2021, 5, 56. [Google Scholar] [CrossRef]
- Kirner, R.; Raffaelli, L.; Rolt, A.; Laskaridis, P.; Doulgeris, G.; Singh, R. An assessment of distributed propulsion: Part B – Advanced propulsion system architectures for blended wing body aircraft configurations. Aerosp. Sci. Technol. 2016, 50, 212–219. [Google Scholar] [CrossRef]
- Gohardani, A.S.; Doulgeris, G.; Singh, R. Challenges of future aircraft propulsion: A review of distributed propulsion technology and its potential application for the all electric commercial aircraft. Prog. Aerosp. Sci. 2011, 47, 369–391. [Google Scholar] [CrossRef]
- Nickol, C.L.; Haller, W.J. Assessment of the Performance Potential of Advanced Subsonic Transport Concepts for NASA’s Environmentally Responsible Aviation Project. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; p. 1030. [Google Scholar]
- Connolly, J.W.; Chapman, J.W.; Stalcup, E.J.; Chicatelli, A.; Hunker, K.R. Modeling and Control Design for a Turboelectric Single Aisle Aircraft Propulsion System. In Proceedings of the 2018 AIAA/IEEE Electric Aircraft Technologies Symposium (EATS), Cincinnati, OH, USA, 12–14 July 2018; pp. 1–19. [Google Scholar]
- Nguyen, N.T.; Reynolds, K.; Ting, E.; Nguyen, N. Distributed Propulsion Aircraft with Aeroelastic Wing Shaping Control for Improved Aerodynamic Efficiency. J. Aircr. 2018, 55, 1122–1140. [Google Scholar] [CrossRef]
- Zhang, J.; Kang, W.; Li, A.; Yang, L. Integrated flight/propulsion optimal control for DPC aircraft based on the GA-RPS algorithm. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 230, 157–171. [Google Scholar] [CrossRef]
- Lei, T.; Kong, D.; Wang, R.; Li, W.; Zhang, X. Evaluation and optimization method for power systems of distributed electric propulsion aircraft. Acta Aeronaut. Et Astronaut. Sin. 2021, 42, 624047. (In Chinese) [Google Scholar] [CrossRef]
- Da, X.; Fan, Z.; Xiong, N.; Wu, J.; Zhao, Z. Modeling and analysis of distributed boundary layer ingesting propulsion system. Acta Aeronaut. Et Astronaut. Sin. 2018, 39, 122048. (In Chinese) [Google Scholar] [CrossRef]
- Liu, C.; Si, X.; Teng, J.; Ihiabe, D. Method to Explore the Design Space of a Turbo-Electric Distributed Propulsion System. J. Aerosp. Eng. 2016, 29, 04016027. [Google Scholar] [CrossRef]
- Choi, B.; Brown, G.V.; Morrison, C.; Dever, T. Propulsion Electric Grid Simulator (PEGS) for Future Turboelectric Distributed Propulsion Aircraft. In Proceedings of the 12th International Energy Conversion Engineering Conference, Cleveland, OH, USA, 28–30 July 2014; p. 3644. [Google Scholar]
- Rothhaar, P.M.; Murphy, P.C.; Bacon, B.J.; Gregory, I.M.; Grauer, J.A.; Busan, R.C.; Croom, M.A. NASA Langley Distributed Propulsion VTOL TiltWing Aircraft Testing, Modeling, Simulation, Control, and Flight Test Development. In Proceedings of the 14th AIAA Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 16–20 June 2014; p. 2999. [Google Scholar] [CrossRef] [Green Version]
- Freeman, J.L.; Klunk, G.T. Dynamic Flight Simulation of Spanwise Distributed Electric Propulsion for Directional Control Authority. In Proceedings of the 2018 AIAA/IEEE Electric Aircraft Technologies Symposium, Cincinnati, OH, USA, 9–11 July 2018; Volume 2018, pp. 1–15. [Google Scholar] [CrossRef]
- Kratz, J.L.; Thomas, G.L. Dynamic Analysis of the STARC-ABL Propulsion System. In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IN, USA, 19–22 August 2019. [Google Scholar]
- Van, E.N.; Alazard, D.; Döll, C.; Pastor, P. Co-design of aircraft vertical tail and control laws using distributed electric propulsion. IFAC-Pap. 2019, 52, 514–519. [Google Scholar] [CrossRef]
- Van, E.N.; Alazard, D.; Döll, C.; Pastor, P. Co-design of aircraft vertical tail and control laws with distributed electric propulsion and flight envelop constraints. CEAS Aeronaut. J. 2021, 12, 101–113. [Google Scholar] [CrossRef]
- Garrett, M.; Avanesian, D.; Granger, M.; Kowalewski, S.; Maroli, J.; Miller, W.A.; Jansen, R.; Kascak, P.E. Development of an 11 kW lightweight, high efficiency motor controller for NASA X-57 Distributed Electric Propulsion using SiC MOSFET Switches. In Proceedings of the AIAA (American Institute of Aeronautics and Astronautics) Propulsion and Energy 2019 Forum, Indianapolis, IN, USA, 19–22 August 2019; pp. 1–8. [Google Scholar]
- Klunk, G.T.; Freeman, J.L. Vertical Tail Area Reduction for Aircraft with Spanwise Distributed Electric Propulsion. In Proceedings of the 2018 AIAA/IEEE Electric Aircraft Technologies Symposium, Cincinnati, OH, USA, 9–11 July 2018; p. 5022. [Google Scholar] [CrossRef]
- Suzuki, Y.; Dunham, W.; Kolmanovsky, I.; Girard, A. Failure Detection and Control of Distributed Electric Propulsion Aircraft Engines. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; p. 0109. [Google Scholar]
- Shah, R.; Sands, T. Comparing Methods of DC Motor Control for UUVs. Appl. Sci. 2021, 11, 4972. [Google Scholar] [CrossRef]
- Koo, S.M.; Travis, H.D.; Sands, T. Evaluation of Adaptive and Learning in Unmanned Systems. Preprints 2022. [Google Scholar] [CrossRef]
- Chakraborty, I.; Ahuja, V.; Comer, A.; Mulekar, O. Development of a Modeling, Flight Simulation, and Control Analysis Capability for Novel Vehicle Configurations. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; p. 3112. [Google Scholar]
- Armstrong, M.; Ross, C.; Phillips, D.; Blackwelder, M. Stability, Transient Response, Control, and Safety of a High-Power Electric Grid for Tur-Boelectric Propulsion of Aircraft; NASA/CR 2013-217865; National Aeronautics and Space Administration: Cleveland, OH, USA, 2013.


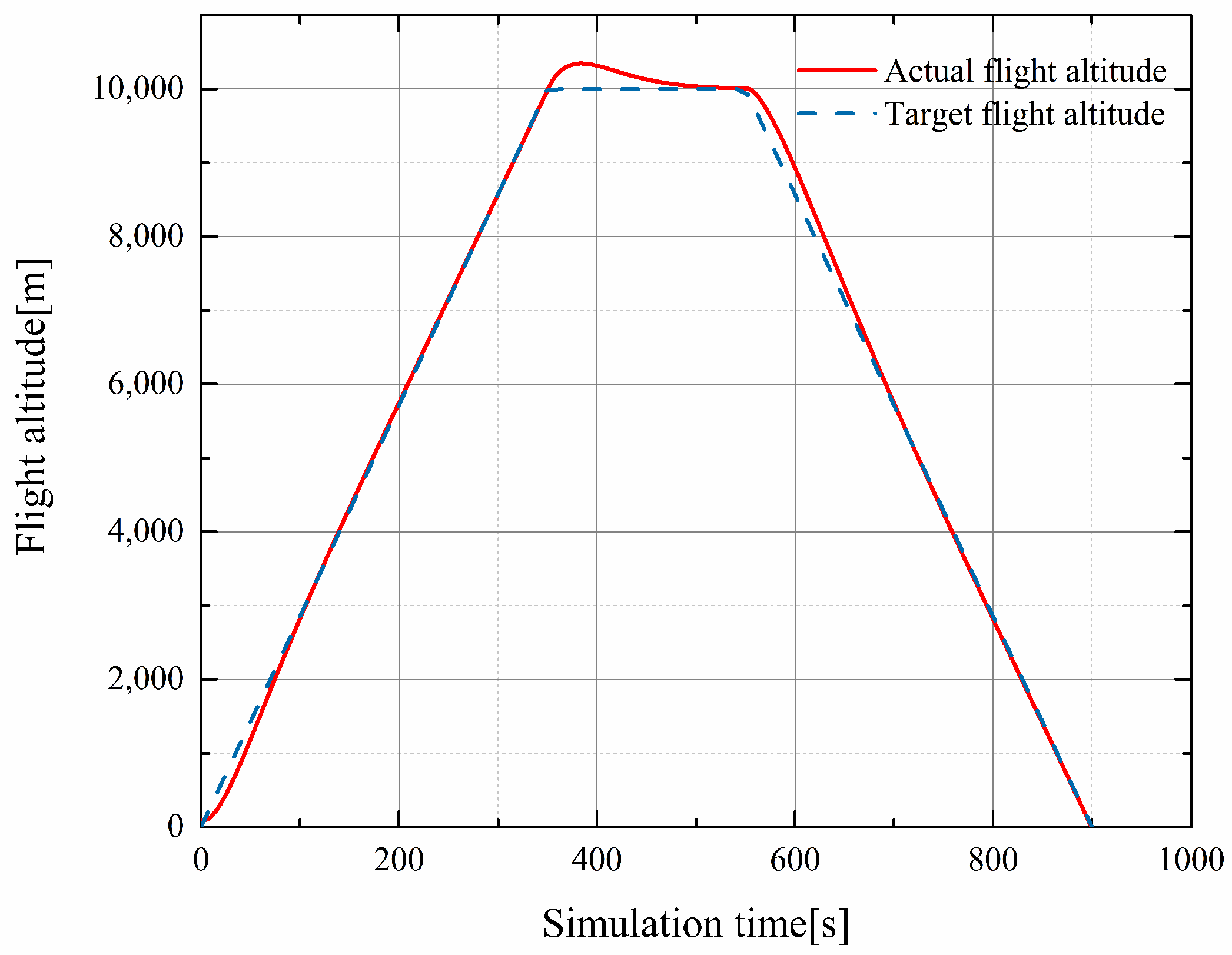
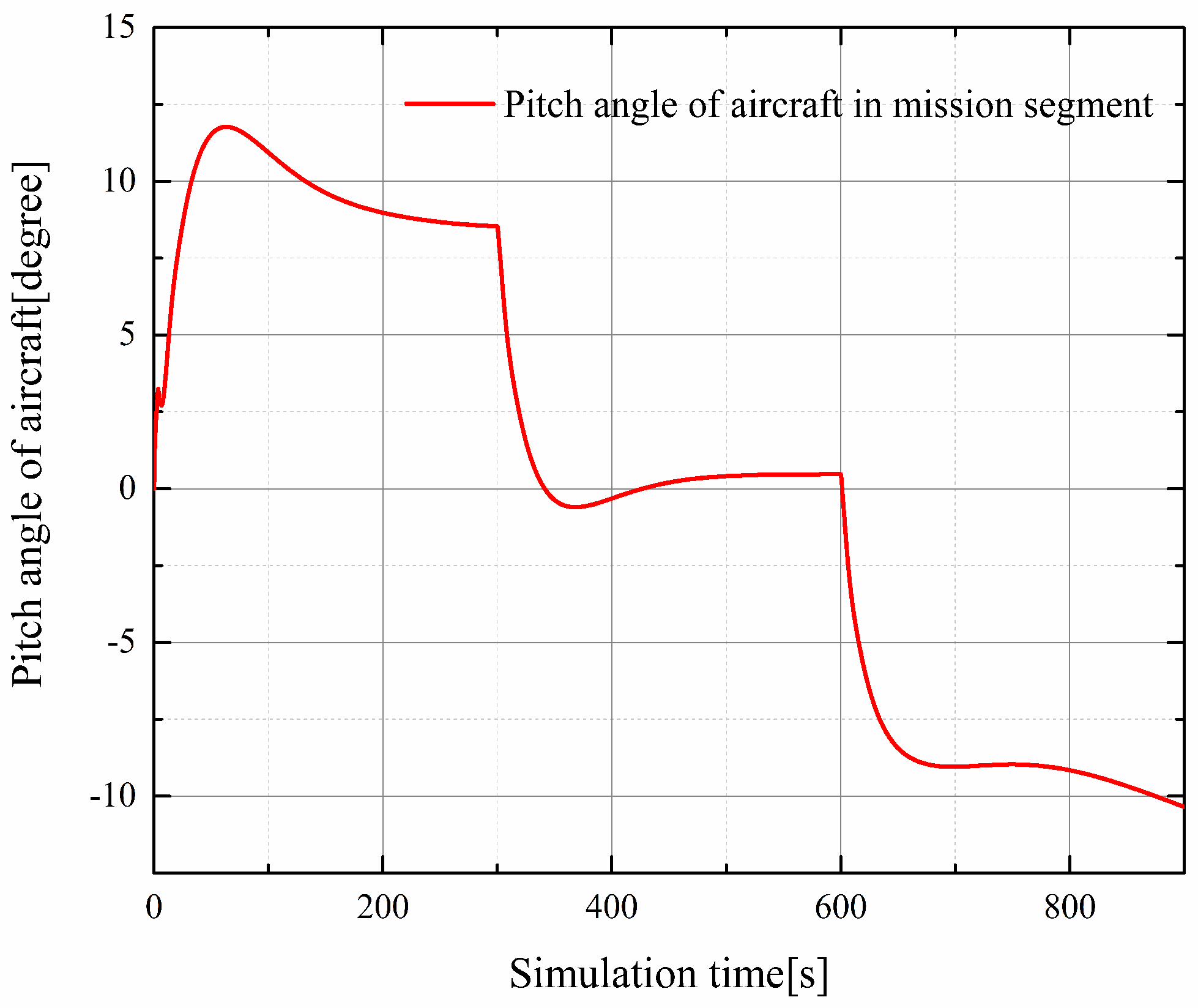
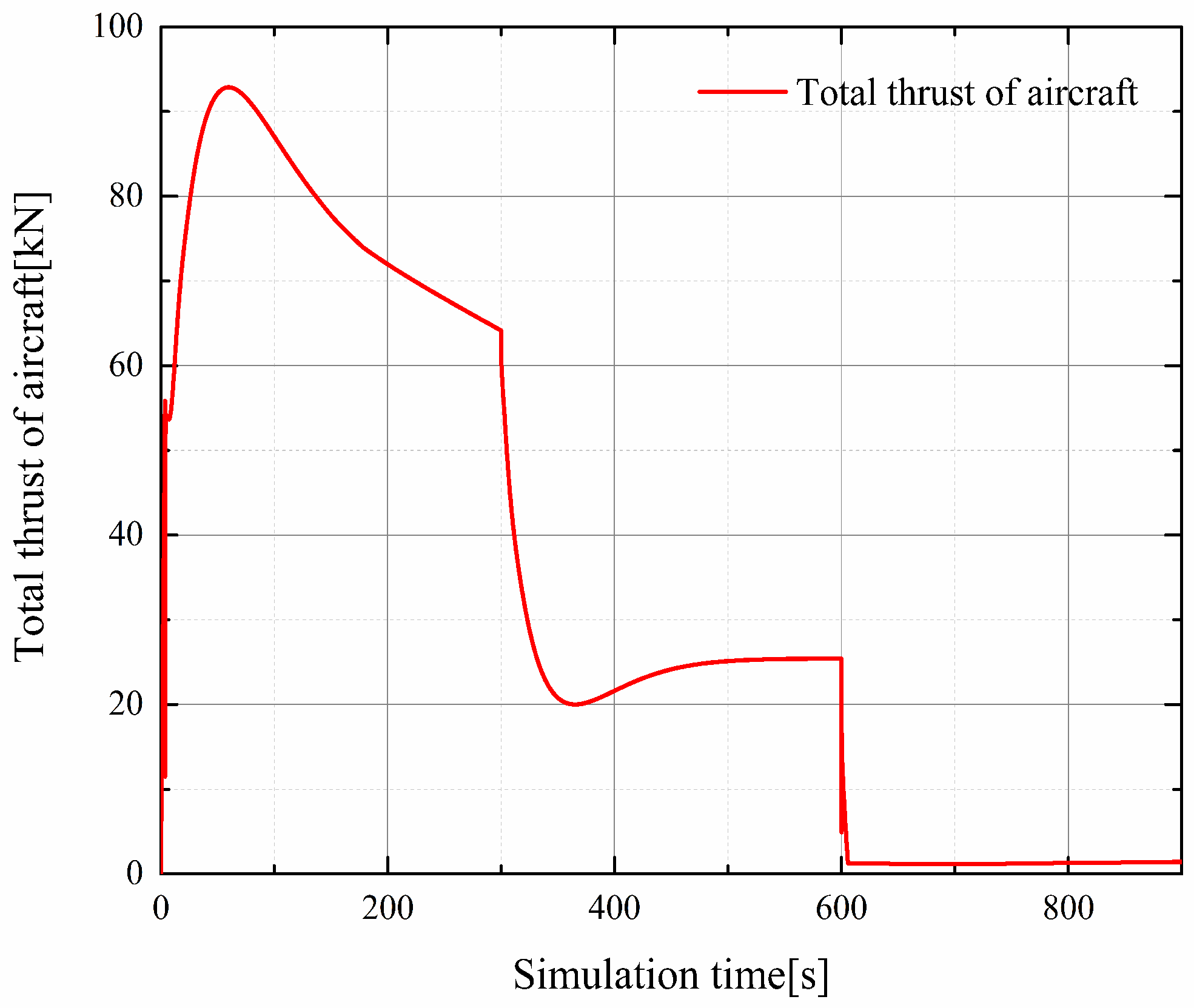
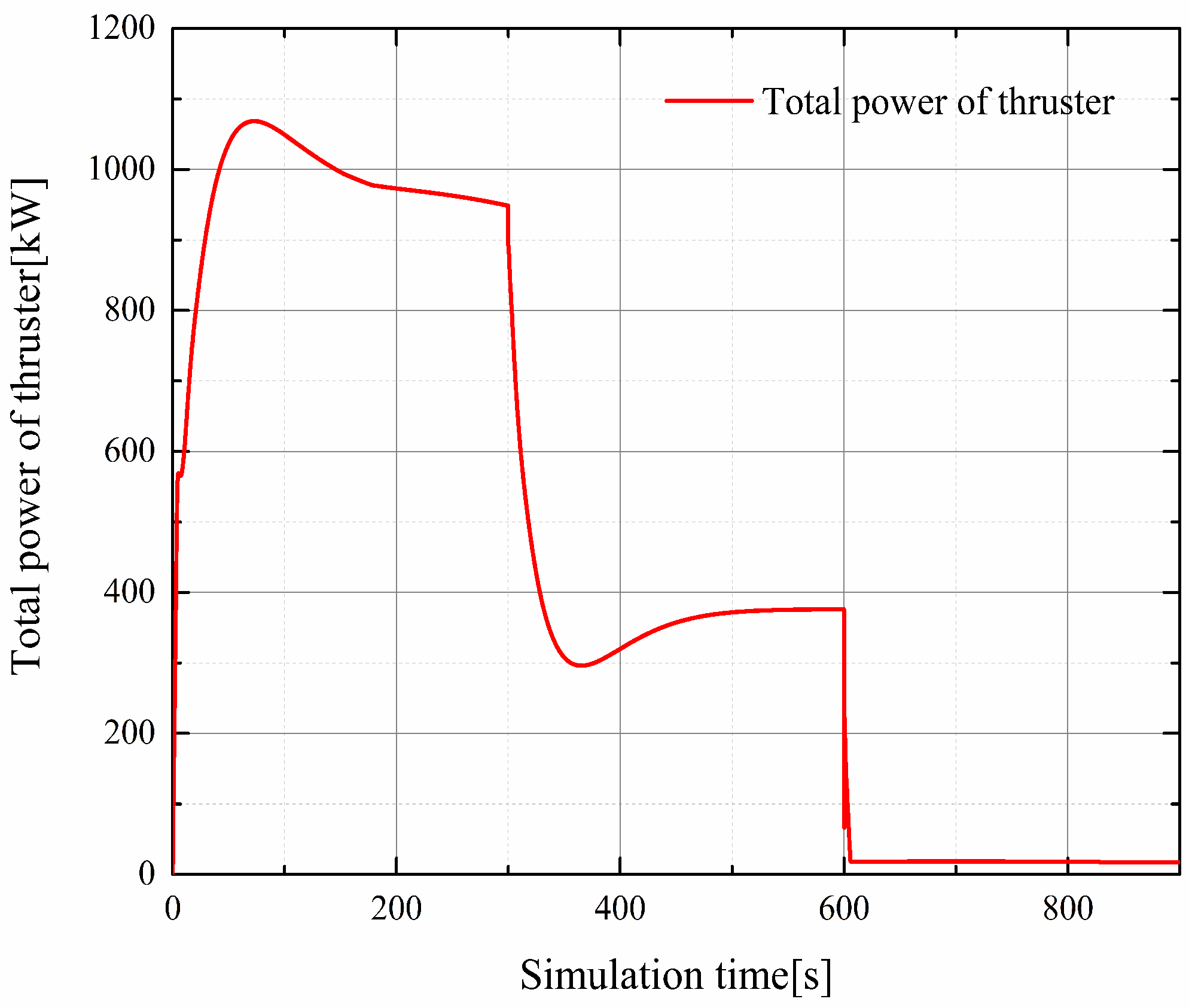
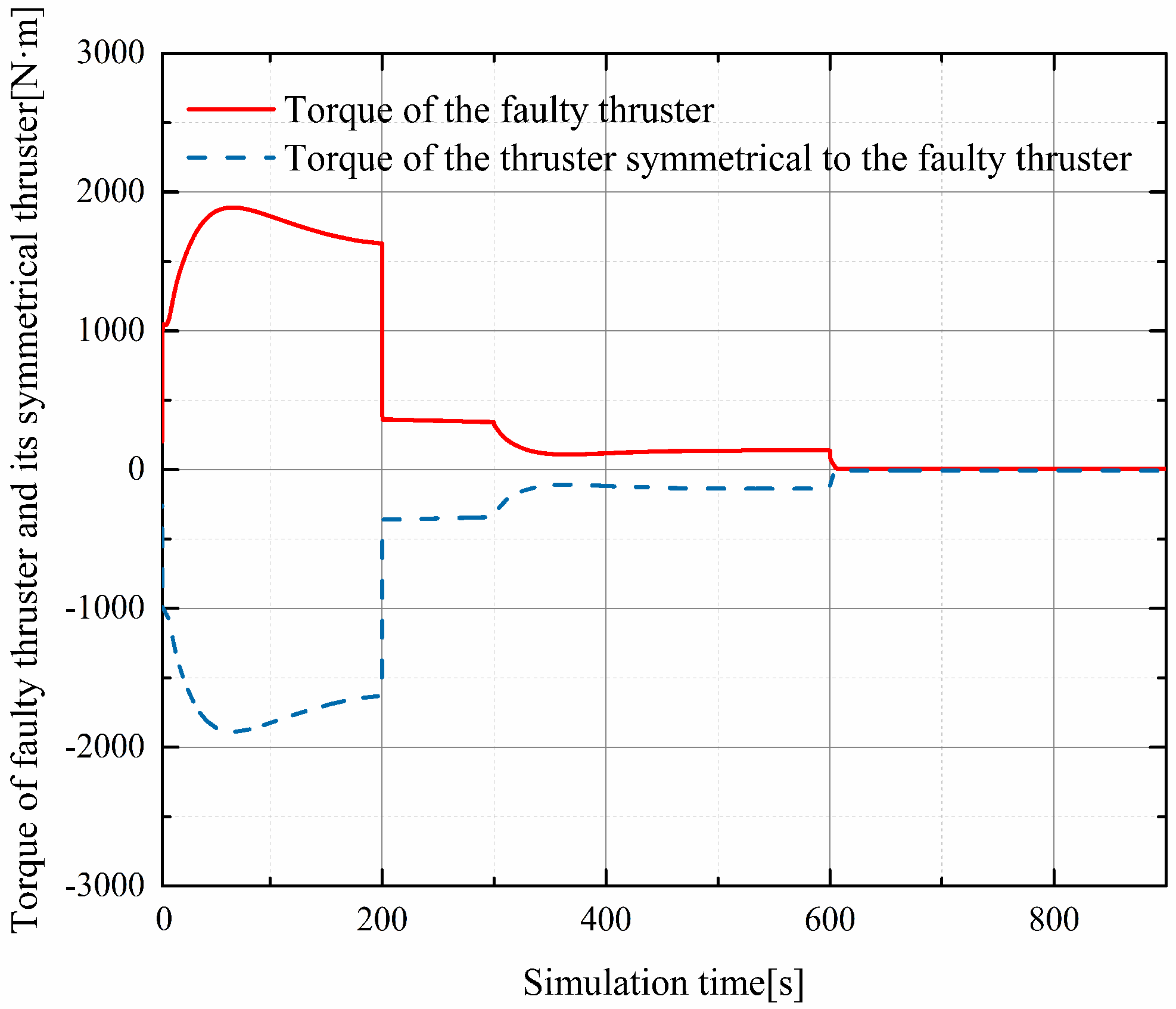

| Flight Phase | Starting Height (m) | Final Height (m) | Mach Number |
|---|---|---|---|
| Climb | 0 | 10,000 | 0.49 |
| Cruise | 10,000 | 10,000 | 0.79 |
| Descent | 10,000 | 0 | 0.18 |
| Performance Index | Value | Unit |
|---|---|---|
| Rise time | 349.75 | seconds |
| Peak time | 375.97 | seconds |
| Settling time | 493.61 | seconds |
| Overshoot | 3.46 | percent |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Yang, J.; Zhang, H. Research on Modeling and Fault-Tolerant Control of Distributed Electric Propulsion Aircraft. Drones 2022, 6, 78. https://doi.org/10.3390/drones6030078
Li J, Yang J, Zhang H. Research on Modeling and Fault-Tolerant Control of Distributed Electric Propulsion Aircraft. Drones. 2022; 6(3):78. https://doi.org/10.3390/drones6030078
Chicago/Turabian StyleLi, Jiacheng, Jie Yang, and Haibo Zhang. 2022. "Research on Modeling and Fault-Tolerant Control of Distributed Electric Propulsion Aircraft" Drones 6, no. 3: 78. https://doi.org/10.3390/drones6030078
APA StyleLi, J., Yang, J., & Zhang, H. (2022). Research on Modeling and Fault-Tolerant Control of Distributed Electric Propulsion Aircraft. Drones, 6(3), 78. https://doi.org/10.3390/drones6030078






