Homogeneous Agent Behaviours for the Multi-Agent Simultaneous Searching and Routing Problem

Abstract

Through the use of autonomy Unmanned Aerial Vehicles (UAVs) can be used to solve a range of of multi-agent problems that exist in the real world, for example search and rescue or surveillance. Within these scenarios the global objective might often be better achieved if aspects of the problem can be optimally shared amongst its agents. However, in uncertain, dynamic and often partially observable environments centralised global-optimisation techniques are not achievable. Instead, agents may have to act on their own belief of the world, making the best decisions independently and potentially myopically. With multiple agents acting in a decentralised manner how can we discourage competitive behaviour and instead facilitate cooperation. This paper focuses on the specific problem of multiple UAVs simultaneously searching for tasks in an environment whilst efficiently routing between them and ultimately visiting them. This paper is motivated by this idea that collaboration can be simple and achieved without the need for a dialogue but instead through the design of the individual agent’s behaviour. By focusing on what is communicated we expand the use of a single agent behaviour. Which through minor modifications can produce distinct agents demonstrating independent, collaborative and competitive behaviour. In particular by investigating the role of sensor and communication ranges this paper will show that increased sensor ranges can be detrimental to system performance, and instead the simple modelling of nearby agents’ intent is a far better approach.

1. Introduction

Unmanned Aerial Vehicles (UAVs) are a potential and exciting solution to a number of real-world problems such as reconnaissance and surveillance [1,2,3,4,5,6,7], search and rescue [8,9,10], and package delivery [11,12]. In particular, utilising multiple UAVs simultaneously can result in these problems being solved faster, more efficiently and more robustly [13] than traditional manned systems. Modelling and planning for multi-agent problems can often be difficult due to a rapidly growing decision space, made increasing complex through agents interactions with each other and the environment. Additionally, this can result in a need for coordination and communication that may not be possible in many situations [14,15]. Many UAV platforms and off- the-shelf solutions are designed in isolation and typically offer only single-agent behaviours. Unless agents have been designed for multi-agent settings or can be coordinated via some centralised control, then behaviour homogeneity might be unavoidable.

This paper looks at the problem of a team of homogeneous UAVs searching, routing and visiting a number of locations (tasks) in the environment. The motivation being that collaboration can still be achieved without the need for an explicit dialogue but instead through the careful design of the agents’ individual behaviours. In particular focusing on what is communicated between agents or what agents think about other agents actions can produce distinct results. These can demonstrate independent, collaborative and competitive behaviour. In particular by exploring the role of sensor and communication ranges this paper will show that increased observability of the state of the world, through increased communication or visual range can in fact be detrimental to system performance. Instead being more prudent with the information an agent has through simple modelling of nearby agents’ intent is a much more fruitful approach.

This paper will begin by outlining the Multi-Agent Simultaneous Searching and Routing Problem (MSSRP), describing the full global optimisation problem statement and then carefully describing how our problem differs and our proposed heuristic approach to find solutions. Then in Section 3 we outline four agent behaviours built from making small modifications to a base-behaviour. Section 4 describes the multi-agent simulation environment developed for testing these agent behaviours. This simulation environment is then used in Section 5 to evaluate the effect of a range of agent parameter choices has on system performance.

2. The Multi-Agent Simultaneous Searching and Routing Problem

The Multi-Agent Simultaneous Searching and Routing Problem (MSSRP) explored in this paper can be summarised as the problem of simultaneously searching for tasks in an environment whilst simultaneously routing between them. This essentially amounts to each agent continuously following their current best route between their known tasks and then re-optimising as new tasks are discovered. One major issue for multiple agents is the potential for massive inefficiencies from agents ‘competing’ for the same tasks. In a centralised problem, given full knowledge of tasks locations, all tasks could be optimally assigned to each UAV ahead of time. However, in this decentralised case we have several key differences (1) UAVs discover tasks by flying around the world and being in close enough proximity to ‘see’ tasks. Thus exploration is an important and necessary factor. (2) UAVs can communicate with other UAVs within a defined proximity in a decentralised manner, giving them the chance to share tasks they have found. (3) UAVs can potentially model other UAVs intent to compete for a task and instead prioritise less-contested tasks.

2.1. The Routing Problem Statement

We will start by defining the global co-operative routing problem of multiple UAVs with full observably, i.e., the searching part of the problem is solved and we know ahead of time the entire set of tasks to visit. However, as we will discuss, our problem differs in the following key ways: (1) Partial Observability of task locations; (2) Agents are working in a decentralised manner; (3) The problem is non-stationary, with agents moving and with tasks being found or being completed over time; (4) Agents are not confined to start and end at a depot.

First define the indexes i and j to denote tasks from the set of tasks T from 1 to N. The set A of agents from 1 to M and the matrix $C_{ija}$ to denote the cost of agent a travelling from task i to task j. We additionally define the three-index binary decision variable:

$$x_{ija}=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\mathrm{agent}a\mathrm{visits}\mathrm{task}j\mathrm{immediately}\mathrm{after}\mathrm{task}i,\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(1)

The formulation is then as follows:

$$\underset{x_a}{min} Z$$

(2)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}..& \sum _{i=1}^N\sum _{j=1}^N{C}_{ij0}{x}_{ij0}\le Z\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill & \sum _{i=1}^N\sum _{j=1}^N{C}_{ij1}{x}_{ij1}\le Z\hfill \\ \hfill & \phantom{b=}⋮\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & \sum _{i=1}^N\sum _{j=1}^N{C}_{ijM}{x}_{ijM}\le Z\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & \sum _{i=1}^N\sum _{a=1}^M{x}_{ija}=1,\forall j\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & \sum _{i=1}^N{x}_{ipa}-\sum _{j=1}^N{x}_{pja}=0,a\in A,p\in T\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & \sum _{j=1}^N{x}_{1ja}=1,\forall a\in A\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & u_i-u_j+N\sum _{a=1}^M{x}_{ija}\le N-1,\forall i\ne j\ne 1\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & x_{ija}\in \{0,1\}\forall i,j,a\hfill \end{array}$$

(10)

Usually MATSPs seek to minimise the either total distance travelled or time taken, which for fixed speeds (as in our case) is equivalent. For our problem we want to complete all the tasks as quickly as possible and so we look to minimise our maximum agent-time Z. Thus the objective, Equation (2), is to minimise the ‘dummy’ variable Z. The constraints Equations (3)–(5) enforce that Z represents the maximum individual agent distance, and thus minimising Z ensures a min-max of individual agent distance. Notably, for agents travelling at fixed speeds this min-max equates to simultaneous time-to-visit all tasks which later will become our metric of performance. The remaining constraints are Equation (6) that ensures each task is visited only once while the flow conservation constraints of Equation (7) state that once an agent visits a task then they must also depart from it. The constraints of Equation (8) ensure each agent is used only once. Equation (9) are sub-tour elimination constraints [16] which rule out any solutions made of non-connected sub-tours. There are a number of approaches to eliminating sub-tours, here we use the Miller–Tucker–Zemlin (MTZ) formulation which uses the idea of ‘node potentials’ [17]. Here u are additional integer auxiliary decision variables, with $u_i$ corresponding to the ith task. These decision variables assign a number to each task and enforce that the order of vertices visited within the tour correspond to sequential values of u. This ensures that for each agent we find at most a single tour.

The formulation above gives the global optimisation problem, given full information of tasks and centralised cooperation between Agents. Due to the NP hard [18] nature of the MATSP means it does not scale well with increasing the number of variables or constraints. That is if we increase the number of agents and/or the number of tasks in the problem we can quickly run into problems which would require a prohibitively long time to solve. Thus a direct solution approach can be impractical and additionally is also ill suited for a decentralised implementation let alone one that is partially observable. To meet the needs of solving our decentralised, partial-information, searching and routing problem we make some important adjustments.

2.2. Partial-Observability of Task Locations

As the problem of this paper is inherently a searching problem this implies that the tasks themselves are not known ahead of time. Constraints on aspects of a UAV vision and communication mean that they might not be able to sense the entire state of the world at once. Additionally, as agents in this environment act simultaneously and independently means that the problem is Partially Observable (PO). Instead over time through exploration, visual sensing and, communication between agents can lead to knowing more about the current state of the world. Importantly, for each agent a, it holds its own understanding of the state and thus its own set of tasks $T_a\subseteq T$.

2.3. Decentralised Agents

Each agent, a, searches the space and adds any new tasks it finds its task list, $T_a$. As will be outlined in Section 3 agents may also be able to share these tasks lists with other nearby agents. However, as full communication may not always be possible and each agent is subject to partial observability there cannot reasonably exist a single, centralised solution to the formulation of Equations (2)–(9). Instead agents act in a decentralised manner looking to solve a TSP for its own list of tasks $T_a$. Thus reducing the problem to a series of, potentially overlapping, Single Agent Travelling Salesman Problem (SATSP). Helpfully, solving a SATSP is almost always much simpler than solving a MATSP. Additionally the fact the task list is the partially observed subset $T_a\subseteq T$, means that each SATSP should be easier still due to a smaller set of tasks. These two factors mean that we are able to rely on simple heuristic approaches to solve each agent’s SATSP, these approaches will be discussed in Section 2.6.

2.4. Non-Stationarity

As a result of the Partial Observability, the decentralised nature of the agents, the movements of the agents and the fact tasks are being completed as time passes means that the problem is non-stationary. A solution which is optimal in one time-step may no longer be in the next. Therefore, instead of finding a single global solution for all agents at time $t=0$, we instead must act dynamically and re-solve at every time-step to take into account new information. This means there must also be in an iterative updating of C. Thus this temporal effect on C, the decentralised nature of the agents and their independent knowledge of task locations means that a global three-dimensional cost matrix C is not congruent nor feasible. Instead each agent must maintain its own two-dimensional cost matrix $C_{ij}$, where at each timestep its shape might change due to changing tasks and its values need updating to reflect the new position of the agent.

2.5. No Fixed Depot

Due to the dynamic nature of the problem we relax the normal TSP constraint that agents must start or finish at a depot (or fixed location). This is achieved by representing the agents’ location as dummy tasks, essentially acting as their own personal depot. Along with this an asymmetric extension is made to the cost matrix $C_{ij}$, whereby the cost, $C_{aj}$, is calculated as normal to go from the agent’s current location (its dummy-task) to each of the other tasks, but the cost to complete the tour, $C_{ja}$, (i.e., travel from a final task to the dummy agent-task) is zero.

2.6. Heuristic Solution Process

As we no longer demand a full, globally optimal solution to the formulation of Equations (2)–(9) we can rely on the use a number of heuristic solutions to provide good solutions quickly and reliably. Additionally, due to the dynamic nature of the problem the route optimisation is done each time step to take into account any new information (such as new tasks). Therefore, we use fast heuristic approaches to find approximate solutions to the SATSP. At each time-step each agent, a, calculates its cost matrix $C_{ij}$ and performs, at random, one of two heuristic routines (called $H_{\mathrm{exhaustive}}$ and $H_{2\mathrm{opt}}$) to try to improve its current route.

The first Heuristic $H_{\mathrm{exhaustive}}$ is a brute force exhaustive search approach and is outlined in Algorithm 1. Each agent a, has a cost matrix $C_{ij}$ and a current route r. This route r is the ordered list of tasks to visit, and is simply a different representation of the matrix $x_{ij}$ of Equation (1). This current route could be the previously found good route or a random initialisation. We can calculate the route’s cost with the following function:

$$\mathbf{evalRoute}(r,C)=\sum _{i=1}^{L_r-1}C[r\left[i\right],r[i+1]]$$

(11)

where $L_r$ is the length of the route r. This function is equivalent to the left hand side of Equation (3), but instead applied to an ordered list of tasks. The Heuristic $H_{\mathrm{exhaustive}}$ checks the cost of each of the possible route-order permutations, returning the one, $r^{*}$, with the lowest cost $c^{*}$.

Algorithm 1 $H_{\mathrm{exhaustive}}$ solver for the SATSP.

Input:C, r, perm_limit  $c^{*},r^{*}\leftarrow \mathbf{evalRoute}(r,C),r$              ▹ Current best cost and route  $\text{R\_perms}\leftarrow \mathbf{permGenerator}(r,\text{perm\_limit})$      ▹ Generate all permutations  for $r^{\prime }\in \text{R\_perms}$ do      $c^{\prime }\leftarrow \mathbf{evalRoute}(r,c^{\prime })$               ▹ Get cost of potential route      if $c^{\prime }<c^{*}$ then          $c^{*},r^{*}\leftarrow c^{\prime },r^{\prime }$                  ▹ Update best cost and route      end if  end for  return$r^{*},c^{*}$

The number of possible permutations grows exponentially with the size of the route, or more precisely with the factorial of the route length $L_r!$. Therefore an evaluation limit, denoted perm_limit, is imposed. The generator function permGenerator, outlined in Algorithm 2, randomly chooses and returns one of the possible route permutations possible. If the number of possible permutations exceeds perm_limit then we will be unable to exhaustively test all permutations. Importantly, permGenerator ensures a random set of permutations each time, so as to not bias our results towards checking through a static ordering. First define a permutation index, i, to refer to the ith possible permutation from the set of all permutations. Then by randomly sampling from the range of possible permutation indexes we can create a sample set $\{X_1,\cdots ,X_{perm\_limit}\}$ the same size as the perm_limit. This set can then be used to generate a subset of permutations. Algorithm 2 uses divmod (also know as Euclidean division) to get the quotient and divisor and then uses those with a form of the Fisher-Yates shuffle [19] to produce these indexed permutations.

Algorithm 2 permGenerator - Limited permutation generator.

Input: r, perm_limit  $L_r\leftarrow \mathbf{length}\left(r\right)$  $\text{no\_perms}\leftarrow min(L_r!,\text{perm\_limit})$         ▹ Get total allowable permutations  $\mathrm{pIndexes}\leftarrow \{X_1,\cdots ,X_{perm\_limit}\}\sim \mathcal{U}\left([1,\cdots ,\text{no\_perms}]\right)$    ▹ Sample indexes  $\text{R\_perms}\leftarrow \left\{\right\}$                  ▹ Keep a running set of permutations  for p in pIndexes do      for $i\leftarrow 1$ to $L_r-1$ do          $p,j\leftarrow \mathbf{divmod}(p,L_r-i)$              ▹ Get quotient and remainder          $r\left[i\right],r[i+j]\leftarrow r[i+j],r\left[i\right]$                     ▹ Swap the elements          $\text{R\_perms}\leftarrow \text{R\_perms}\cup \left\{r\right\}$           ▹ Append to set of permutations      end for  end for  return $\text{R\_perms}$

Our second Heuristic function $H_{2\mathrm{opt}}$ is based on the popular TSP heuristic known as two-opt swap, first proposed by Croes [20] and has been used as a simple but effective heuristic solution for a range of optimisation problems [21,22,23,24]. The aim of the basic two-opt is to take two adjacent nodes, $[\cdots ,v_i,v_{i+1},\cdots ]$, in a route and swap their order, $[\cdots ,v_{i+1},v_i,\cdots ]$, with the idea being that if the paths previously crossed over, by swapping them this might uncross them. The approach of $H_{2\mathrm{opt}}$ is outlined in Algorithm 3 and using this two-opt swapping idea, loop over each node of the route r and applying the two-opt swap. In addition, our approach uses a second neighbourhood loop to look at increasing swap lengths. That is, for a neighbourhood size $N_r$, instead of swapping elements i and $i+1$ we swap all elements i to $i+k$ for $k\in (1,\cdots ,N_r)$. These two loops are somewhat analogous to a breadth vs depth search approach. Like before, we also impose an evaluation limit (eval_limit) to ensure bounded run-times.

Algorithm 3 Two-Opt Heuristic solver $H_{2\mathrm{opt}}$ for the SATSP.

Input:C, r, $N_r$, eval_limit  $c^{*},r^{*}\leftarrow \mathbf{evalRoute}(r,C),r$              ▹ Current best cost and route  $L_r\leftarrow \mathbf{length}\left(r\right)$  $\mathrm{evals}\leftarrow 0$  for $i\leftarrow 1$ to $L_r-1$ do      for $j\leftarrow i+1$ to min$(L_r,i+1+N_r)$ do          if $j-i\ne 1$ then             $r^{\prime }\leftarrow [r[0:i-1]+\mathbf{reverse}\left(r[i:j-1]\right)+r[j:L_r]$     ▹ Swap the order             $c^{\prime }\leftarrow \mathbf{evalRoute}(r^{\prime },C)$             $\mathrm{evals}\leftarrow \mathrm{evals}+1$          end if          if $c^{\prime }<c^{*}$ then             $c^{*},r^{*}\leftarrow c^{\prime },r^{\prime }$                    ▹ Update best cost and route          end if          if $\mathrm{evals}>\text{eval\_limit}$ then               ▹ Check if eval limit reached             Break          end if      end for  end for  return $r^{*},c^{*}$

The nature of this particular search problem means that agents are constantly moving around the world updating their task lists. Therefore what is considered optimal can change rapidly. Thus good solutions are often sufficient and require less computation. These two heuristics also work on slightly different aspects of the solution space. $H_{\mathrm{exhaustive}}$ is entirely brute force stochastic approach, jumping around the global solution space hoping to land on a better solution, whereas $H_{2\mathrm{opt}}$ works to improve an existing route looking locally. Therefore the combination of these two heuristics are more than sufficient for creating good solutions for the individual agents whilst being bounded enough to be run each time step (scaling linearly with the number of agents). Furthermore, as each agent retains in memory its current order of tasks and thus its route, at each future time-step the route can be improved further. Importantly, these methods do not need resolving entirely from scratch like some other optimisation techniques. Instead new tasks can be added to the route at an appropriate location, in this paper new tasks are initially added at the end of the route. By not fundamentally changing the current route it instead assumes that at worst this task is visited after the currently best route. Additionally, by being last in the route, the agent has more time-steps to apply these heuristics and reorder its route to more efficiently visit it.

3. UAV Agent Behaviours

Let us define a ‘base’ agent behaviour, from which other agent behaviours will be derived. This behaviour follows the Agent Based Modelling and Simulation approach [25,26] whereby agents are autonomous, self-directed and self-contained, the agents ‘live’ in the environment and can interact with it and other agents and be acted upon. The simulation involves deploying a number of these agents in the environment and simulating a number of discrete time-steps or until some goal has been achieved. For each time step each UAV agent will:

• Sense: Take in information from the environment through sensing and from other agents through communication
• Plan: Use this information and other information stored in memory to decide a route to follow and/or a direction to move
• Act: Attempt to move in the intended direction and also may communicate with others.

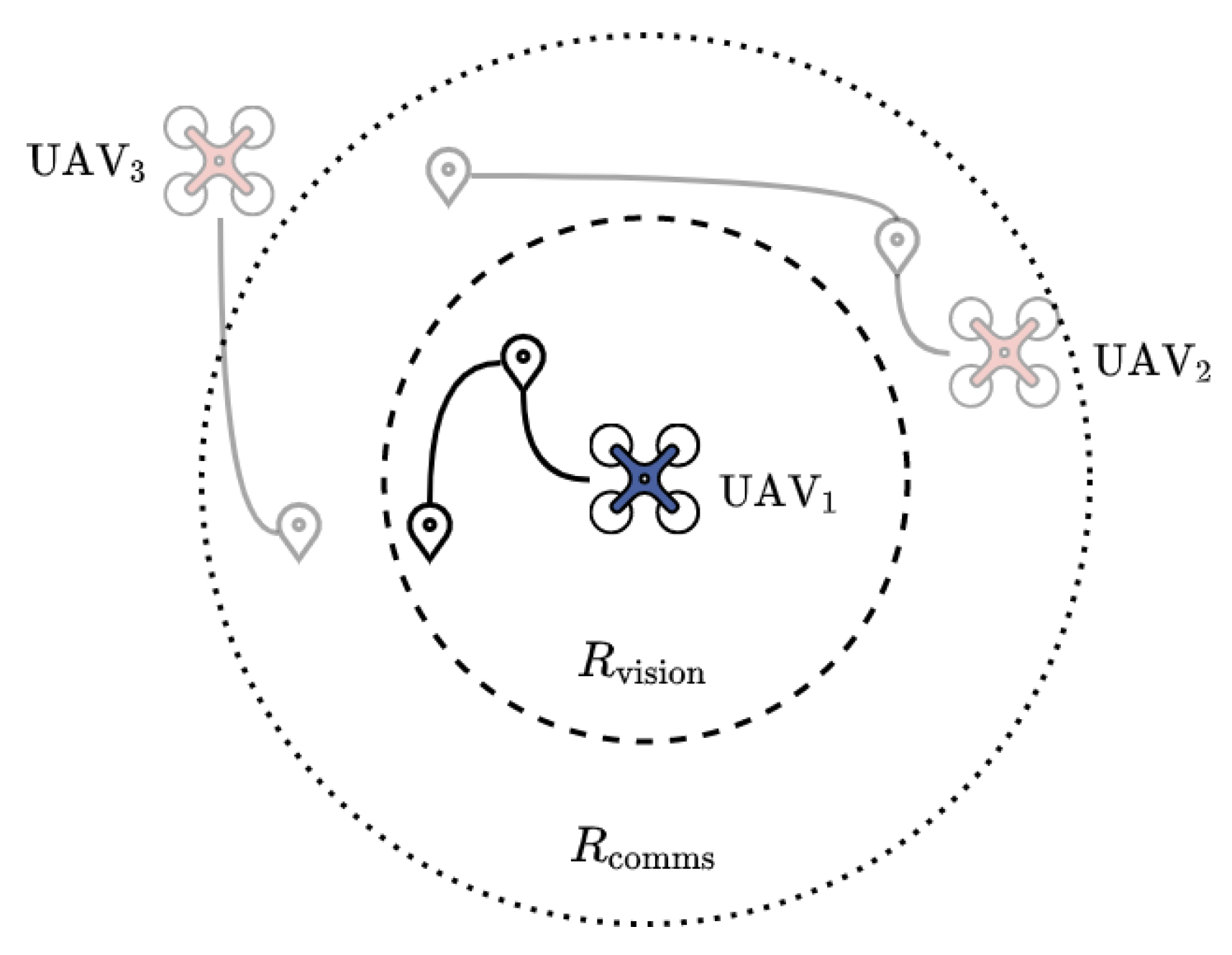
In this paper and outlined in Figure 1 UAVs are able to visually sense a task location. If at that time step a task lies within a defined proximity radius referred to as a ‘vision radius’ $R_{\mathrm{vision}}$ it is considered seen. Additionally, the UAVs have a ‘communication radius’ $R_{\mathrm{comms}}$, which is the radial distance it is able to broadcast to other agents and listen to incoming messages. By looking at Figure 1 one can imagine how ${\mathrm{UAV}}_1$’s decision of which order to complete its tasks could be influenced by the knowledge of other tasks outside its current vision radius. Therefore an agents behaviour will be defined by three key traits:

• Speak: What an agent communicates to others.
• Listen: What an agent does with communications heard.
• Model: What an agent does to model other agents behaviour.

Given these traits a motivating idea behind this paper is the question: can the overall performance of a group of agents be improved if the agents are able to share their known tasks with one another? While it might seem intuitive that knowing more about the world can only improve performance, we will demonstrate in this paper that this is not the case.

Taking those three traits and turning on or off only two of them (listening and modelling) we can augment the base agent to create four distinct behaviours. These four behaviours are detailed in

Table 1. Three agent behaviour types from three base modifications.

Type	Speak	Listen	Model
Solo	Broadcast all tasks	Ignore	None
Greedy	Broadcast all tasks	Add all heard tasks	None
$\mathrm{Solo}+$	Broadcast all tasks	Ignore	Move next competing task
$\mathrm{Greedy}+$	Broadcast all tasks	Add all heard tasks	Move next competing task

and we will refer to them as Solo, Greedy, $\mathrm{Solo}+$ and $\mathrm{Greedy}+$. In Section 4.3 we will go into detail about the speak and listen traits, in particular what, when and how this takes place.

3.1. Modelling Other Agents Intent

The concept of modelling other agents is to try and predict and understand what another agent might do, in an attempt to improve our own decision. For the purposes of this paper this modelling comes in a very simple form based around the question: Will another UAV reach that task first? This is illustrated in Figure 2 whereby two agents, Blue (left) and Red (right), compete for three tasks, A, B and C. Assume that we are the Blue Agent, we are following a route that visits task A then B then C. We do not know what tasks the Red Agent is trying to do but for this example imagine it is trying to visit the exact same three tasks in the same order. In the first scenario the Blue Agent changes nothing and as a result the Red Agent reaches all three tasks first. In the second scenario, the Blue Agent observes (as Red falls within its $R_{\mathrm{vision}}$ range) the position of Red and calculates that it is closer to task A, and by modelling the possible intent to go to task A, decides it can not make it there before Red. It therefore looks to avoid that task for now, by moving task A to the back of its route and going after the next available task (in this case task B). Thus a UAV with the modelling behavioural trait allows it to use the location of another agent to better inform its route plan and hopefully avoid competing for the same tasks and in turn more efficiently complete other tasks instead.

4. Multi-Agent System Simulation Environment

In order to explore the effect of these behaviours and their parameters on performance we need to simulate them. Our main capability requirements for our research is (1) that it is Python based; (2) Has a lightweight Graphical User Interface for demonstration and interrogation of parameters; (3) Ability to run batches of simulations and generate results. We decided that the Python Agent Based Modelling Simulator (ABMS) called MESA [27] met our requirements, providing the core ABMS building blocks and interface. Extensions to the main MESA code were implemented in order to properly simulate the aspects of our MSSRP.

The main building blocks in our set up are Agents, Spaces and Schedules. Agents are the elements that have agency and ’do something’ i.e., move, interact, update. The Space is the environment in which the agents are placed, i.e., a network, a grid, or a continuous space. The agents are also assigned to a scheduler. The role of the scheduler is to make each of the agents step, that is, invoke an agent’s step function and also to control the order in which this takes place. The scheduler can be defined to run in sequence, parallel or as we do in this paper, randomly. Thus a simulation comprises of the Agents being placed in their Space(s) and then at each time-step the scheduler(s) are run and all the corresponding Agents’ step functions are invoked, this continues until some termination condition is met.

4.1. The Environment

The environment in which our simulation takes place is made up of two spaces. A two-dimensional continuous space in which the UAV agents will be placed, and a hexagonal grid space which contains terrain cells. The hex terrain is made up from 4 tile types: sea (blue), shore (yellow), land (green) or hill (dark green). The arrangement of these tiles is generated procedurally with a few placement rules to form random, but sensible, map layouts (as shown in Figure 3). One of the land terrain tiles is selected at random and given the ‘base’ property (and displayed in red), which is the location from which the UAVs will spawn. Importantly we use these layouts to enforce that the placement of tasks in the world is not completely random, instead we restrict tasks to only be spawned on land locations (shore, land, hill), thus augmenting the randomness to be ‘clumpy’. In particular in this instance the terrain serves as a visual representation of the potential task placement locations. One can imagine how the map features such as the number of islands, proportion of land to sea and placement of a starting base might favour different types of agent behaviour and interaction. It is worth clarifying that the hexagonal grid is still a continuous space, and everything that happens in the simulation, such as UAV motion or task placement, is continuous.

4.2. Task Agents

Tasks are simple Agents that are spawned (placed in the environment) and don’t move. They keep track of a number of properties such as number of times it has been visited or whether it is currently occupied. It is also able to determine whether it has been successfully completed, that is, it has been visited by a UAV Agent. As discussed in Section 4.1, for the purposes of this paper, the tasks are constrained to only spawn on shore, land, or hill hexes within the bounds of the environment. A task spawns only once by finding an admissible starting position. It will sample a potential position at random, repeatedly until it finds one that lies within an allowable tile.

4.3. UAV Agents

The UAVs Agents and their behaviours are the core focus of this paper and our simulations. Just like any other Agent in an ABMS they each carry out their step routine when instructed by their scheduler. The step routines of the Tasks and Terrain cells are simple and are mostly used to keep track of values such as occupancy and completion checks. Whereas the step routine of the UAV agents involves things like movement, routing and communication. The following outlines a UAV agent’s step routine:

• Get Visible
• Get Communicable
• Receive Messages (Listen)
• Optimise Route
• Send Messages (Speak)
• Move

4.3.1. Get Visible

Get the visible agents in the environment, this includes tasks and UAVs. From the set of all tasks, T, the Get Visible process finds the subset $Tvis\in T$ for a given agent, a, within the defined radial distance $R_{\mathrm{vision}}$ of the agent’s current location. In particular:

$${\mathrm{Tvis}}_a=\{t_i\in T,\mathrm{for}i\in (1\cdots N)|\mathbf{dist}(A_a,t_i)\le R_{\mathrm{vision}}\}.$$

(12)

The function dist calculates the Euclidean distance (L2 Norm) between any two agent positions. From the set of all agents, A, the Get Visible process also finds the subset $Avis\in A$ for a given agent, a, within the defined radial distance $R_{\mathrm{vision}}$ of the agent’s current location:

$${\mathrm{Avis}}_a=\{A_b\in A,\mathrm{for}b\in (1\cdots M)a\ne b|\mathbf{dist}(A_a,A_b)\le R_{\mathrm{vision}}\}.$$

(13)

4.3.2. Get Communicable

Similarly from the set of all Agents, A, the Get Communicable process finds the subset $Acomms\in A$ for a given agent, a, within the defined radius $R_{\mathrm{comms}}$. This is done using the following equation:

$${\mathrm{Acomms}}_a=\{A_b\in A,\mathrm{for}b\in (1\cdots M)a\ne b|\mathbf{dist}(A_a,A_b)\le R_{\mathrm{comms}}\}.$$

(14)

One can imagine a situation where agents having a distinct mix of values of $R_{\mathrm{vision}}$ and $R_{\mathrm{comms}}$ might be of interest. However, for the purposes of this paper we assume all UAVs are homogeneous and thus share the same values for $R_{\mathrm{vision}}$ and the same values for $R_{\mathrm{comms}}$.

4.3.3. Receive Messages (Listen)

For all other agents within the set ${\mathrm{Acomms}}_a$ agent a can receive any messages sent in a previous time step. This process is carefully controlled by the simulator to ensure messages are kept for only a single time-step and only received when within the appropriate $R_{\mathrm{comms}}$ distance and the agent behaviour allows it. As outlined in Table 1 an agent’s behaviour might dictate it use or ignore this information. In this work the only messages that can be sent (and thus also received) are a list of tasks and their locations. When an agent receives a list of tasks, if allowed, it adds any new tasks to the end of its current task list.

4.3.4. Optimise Route

For the agent’s current task list it must now decide on the best order in which to visit the tasks. The order of this task list implicitly defines a point-to-point route the UAV is then able to follow. In order to ensure this route is as efficient as possible the agent uses the two heuristic solutions to the TSP as outlined in Section 2.6.

Additionally, it is here where the modelling of other agents’ intent can be incorporated. This is done by using the set of nearby visible agents ${\mathrm{Avis}}_a$ of Equation (13) and the method described in Section 3.1. That is, if the next task to be visited is closer to any another agent in ${\mathrm{Avis}}_a$ then we predict that the task will be visited by another agent first and instead we move that task to the end of our current route.

4.3.5. Send Messages (Speak)

Agents are now able to broadcast information (with no guarantee it will be heard). In this paper that information is the list of all tasks known to that agent. Again, the simulator ensures that this information is only received by the appropriate agents.

4.3.6. Move

Agents finish their step routine by moving, that is, simulating forward their dynamics by a single time step, $dt$. At each time step the UAV agent must choose two things, a desired directionv (a 2 dimensional velocity vector) to move and a desired speeds to move at. These two choices are then passed to the agent’s control routine to calculate the actual velocity and actual speed produced. The control routine ensures that the agent movement is bounded by their dynamic constraints, such as turning rate, maximum acceleration/deceleration and maximum speed. These control choices are then performed by the agent and the agent moves in the space.

If the UAV agent has a current list of tasks, and thus a route from the Optimise Route process, then the agent will choose to move towards the next task. If instead the agent has no list of tasks it will switch to searching mode. In this work, the searching behaviour is to simply perform a random walk. This is achieved by adjusting the agent’s current direction, $v_i$ by a random amount, $\mathcal{V}$,

$$v_{i+1}^{\prime }=v_i+\mathcal{V}\mathrm{where}\mathcal{V}\sim {\mathcal{U}}_2(a,b)$$

(15)

where ${\mathcal{U}}_2$ is a 2-dimensional uniform distribution. For our simulation we chose the bound to be between $a=-0.125$ and $b=0.125$. In both cases the desired speed, s, of the UAV will start, and always be chosen to be, the maximum speed allowable, which in this paper is 5 m/s.

4.4. Simulation Assumptions

While not a limitation of the problem formulation nor simulation environment, for the purposes of this paper and the results of Section 5, a number of assumptions have been made. Firstly, all UAVs start from the same, single base location (The red hex of Figure 4), but the exact location within that Hex will be random for each UAV. Having multiple possible start locations might lead to a performance benefit in some cases, but exploring it here would only add unnecessary variables. There are no constraints on fuel consumption, each UAV starts with an unlimited amount of fuel and does not consume any over the course of the simulation. If fuel were taken into account then the location of the base location (i.e., the refuelling point) might become a substantial influence on performance. Additionally, the UAVs must remain within the simulation environment bounds and it is the role of the ABMS Space to ensure this by `bouncing’ UAVs back from the edges if they try to leave (we can think of this as a kind of geo-fencing). As tasks are only spawned within the environment bounds, this is only an issue when UAVs are performing a random walk due to having no current tasks. We also ignore any potential collision between UAVs and impose no spatial restriction on them. Finally the UAVs do not need to return to base after completion of all tasks, the simulation is terminated when all tasks have been completed. The actual impact that these assumptions have on our results and conclusions is not investigated here, but provides a series of interesting experiments for further research.

4.5. Example of Single Simulation Run

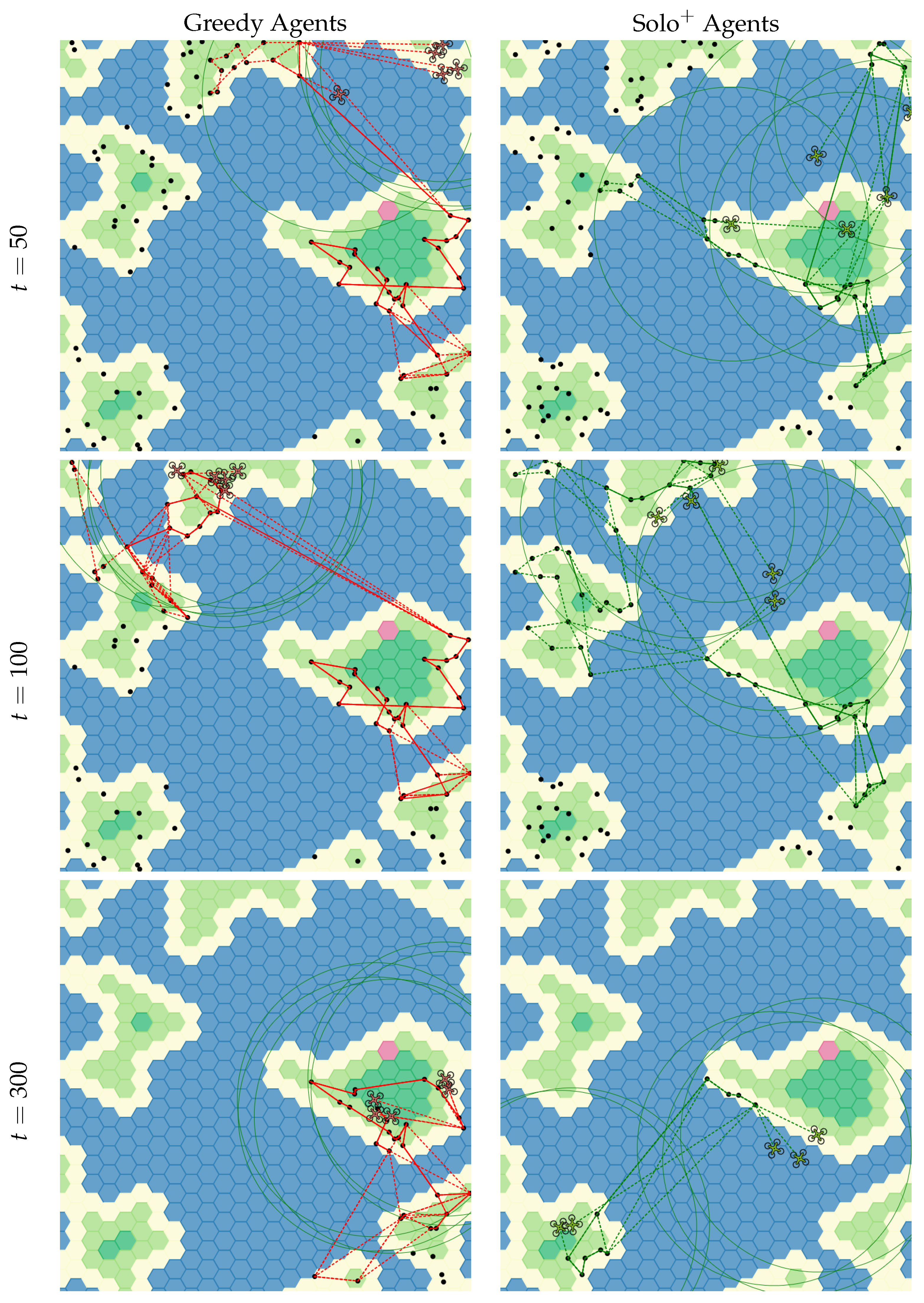
To demonstrate the above-outlined methodology and simulation procedures we now show an example single simulation. This simulation is conducted for two different behaviour types Greedy and ${\mathrm{Solo}}^{+}$. For both examples there are 5 UAVs of the same behaviour type and parameters. Each UAV has a visual range, $R_{\mathrm{vision}}$, of 250 m (which is one third the width and height of the 750 m by 750 m environment). Here, UAVs have a much shorter communication range, $R_{\mathrm{comms}}$, of 50 m (which is one fifteenth the width and height of the environment) meaning they can only communicate with UAVs that are very close to them.

How each simulation run progresses is shown as snapshots in Figure 4 at three different time steps of 50, 100 and 300 (the rows). The black dots represent task locations and dotted lines represent the UAVs current planned route to complete them. As many UAVs have seen, or been told about, the same tasks the UAV routes will often overlap (note that when multiple agents’ dotted lines are plotted they can appear solid). This shared knowledge of the world without explicit cooperation will typically manifest as clusters of UAVs all trying to visit the same tasks at the same time. This results in an inefficient use of the multiple UAVs available. This clustering is clearer in the Greedy Agents of Figure 4 (left column) and with a resulting time of 483 time steps compared to 325 for ${\mathrm{Solo}}^{+}$ (right column). This clustering and competing for the same tasks will be demonstrated further in Section 5 as is a key cause of poor performance.

5. Results and Discussion

We now explore the parameter space of the problem by conducting a series of ensemble simulations. A single simulation trial is defined by its parameters outlined in

Table 2. Fixed and variable Trial Parameters used within the simulation.

Parameter	Description	Value
Max Steps	Maximum allowed time steps	1000
$T_0$	Tasks spawned at start	100
$T_{+}$	Tasks spawned during	0
Environment size	Width and Height of world	750 m × 750 m
Hex Size	centre to vertex distance	25 m
N	Number of UAVs	[2, 5, 10, 20]
$R_{\mathrm{comms}}$	Comms Radius (m)	[50, 250, 1500]
$R_{\mathrm{vision}}$	Vision Radius (m)	[25, 50, 100, 250, 500, 1500]
Behaviour	Agent Behaviour	[Solo, Greedy, $\mathrm{Solo}+$, $\mathrm{Greedy}+$]

. The top half of the table shows the fixed parameters, fixed for all trials, and the remaining variable parameters in the bottom half of the table are swept over. It is the effect the choice of these variable parameters have on overall performance that will be explored in this Section.

A parameter configuration is made up of the 5 static and 4 variable parameters of Table 2 and is run 25 times by testing it against a set of 25 trials. For that parameter configuration every agent within the trial has the same parameters (e.g., are all the same behaviour type with the same $R_{\mathrm{comms}}$, $R_{\mathrm{vision}}$) and are thus homogeneous. We run 25 trials for each of the possible 288 ($4\times 3\times 6\times 4$) different parameter configurations chosen from Table 2. Each of these 25 trials is intialised and generated using a corresponding seed key, so that each parameter combination is tested against a consistent set of trials. The terrain map used for these results is shown in Figure 4 and loaded at the start of the simulation. Each of the 25 seed keys is used to seed a pseudo-Random Number Generator (RNG). This RNG is used to generate the start location of the tasks and UAV agents, as this is seeded it is repeatable, allowing us to create 25 different trials that can be reproduced and tested against each parameter combination. Every other random aspect of the simulation is subject to an entirely different, unique RNG defined by the system clock.

With this in mind we now present the results of our ensemble simulations over the four-dimensional parameter sweep over $R_{\mathrm{comms}}$, $R_{\mathrm{vision}}$, number of UAVs N and Behaviour. As defined in Section 2.1 we look to optimise our objective function Equation (2) which is equivalent to minimising the Timesteps Taken to complete all tasks. The results are presented in Figure 5 and Figure 6 and contain the same data but pivot to focus on either (i) $R_{\mathrm{vision}}$ (as in Figure 5); (ii) $R_{\mathrm{comms}}$ (as in Figure 6); (iii) Number of UAVs (rows); or (iv) Behaviour (lines). For each behaviour/colour the solid line represents the average over the 25 runs and the shaded area represents the spread (standard deviation) of the results.

Starting with the effect of the number of UAVs, in Figure 5 and Figure 6, there is a clear trend. By increasing the number of UAVs from 2 to 20 UAVs (top to bottom) improves the results across all behaviour types. However, while this reduces our particular metric (timesteps taken) it does so inefficiently, doubling the number of agents from 10 to 20 does not result in half the timesteps taken. This inefficiency in scale results in the cumulative timesteps taken by all UAVs, that is $M\times Z$, increases faster than Z decreases. If efficiency was a secondary object then there would be a balance between number of UAVs to deploy and efficient return.

We can easily observe the effect limiting an agents vision, $R_{\mathrm{vision}}$, has on overall performance. Limiting $R_{\mathrm{vision}}$ essentially limits a UAV’s ability to easily find new tasks through searching, this means that simulations with particularly low levels of $R_{\mathrm{vision}}$ (<100 m) perform poorly. On the other hand over a certain level of $R_{\mathrm{vision}}$ values (>1000 m) a UAV can always observe all the tasks no matter where the UAV is, so the searching part of the problem becomes mostly irrelevant. A common shape can be seen in Figure 5 with low $R_{\mathrm{vision}}$ values resulting in poor performance, followed by an optimal value around 250 m and finally a plateau in improvements for higher values. Importantly, for solo and greedy (i.e., without modelling) it is clear that having too much $R_{\mathrm{vision}}$ becomes detrimental to performance. This increases the likelihood of UAVs competing for the same tasks and moving around the space in groups, rather than splitting up. In addition to UAVs competing for the same tasks, having a larger list of tasks likely decreases the efficacy of the heuristic routing solutions of Section 2.6 leading to less-optimal routes.

Interestingly the above trend is not entirely replicated with changes to $R_{\mathrm{comms}}$. Recall that the only difference between solo and greedy behaviour is that greedy agents adds tasks to its list that it hears from other agents, whereas solo agents ignore communications. This means that communication has zero effect on solo and ${\mathrm{solo}}^{+}$ agents. As shown in Figure 5 increasing $R_{\mathrm{comms}}$ from 50 m (left column) to 250 m (right column) does not have a huge effect on performance. Looking in more detail in Figure 6 we can see that for the most part the results response to changing $R_{\mathrm{comms}}$ is mostly flat. The exception to this is for the simulations with greedy and ${\mathrm{greedy}}^{+}$ agents with $R_{\mathrm{vision}}$ of 50 m (left column) which respond negatively to improved communication range. Therefore this highlights that this result agrees with those of increased $R_{\mathrm{vision}}$, adding evidence to the idea that to increase performance, simply knowing about more tasks is not enough. However some of this is likely pathological to the problem definition, due to the spatial nature of a the search, the communication and the homogeneity of agent sensing abilities. A tasks proximity to an agent correlates to its chance of being visited by that agent once it is made aware of it. Indeed being able to inform other far-away agents of tasks near to you, likely has negligible benefits and may serve only to increase the difficulty of the other agents SATSP.

Importantly we can easily observe the effect adding modelling capability to the UAVs, i.e., $\mathrm{Solo}+$ and $\mathrm{Greedy}+$, has on performance. It is clear from Figure 5 that without modelling, increasing $R_{\mathrm{vision}}$ has a significant negative effect on performance. This is due to the fact the UAVs will end up all having a large and similar list of tasks to complete and are more likely to compete for those tasks, acting inefficiently. Specifically, it is the detrimental effect of knowing too much about the world (i.e., more tasks) that is mitigated by adding modelling. One can see that simulations of only 2 UAVs with modelling and $R_{\mathrm{vision}}$ over 250 m can outperform 10 UAVs without modelling. Thus for homogeneous teams of UAVs being smarter about what you do with the information in the environment is much more important than the size of the team. Finally it is worth noting that the variance (the shaded areas) in performance is greatly improved by adding modelling. In fact no other parameter really has any effect on the variance in performance. Therefore without some form of cooperation, which in this case is through modelling, you are leaving the performance of the system up to chance.

The results show that a core contributor to poor multi-agent performance is not effectively distributing the workload of visiting tasks. UAVs with solo behaviour act entirely alone and so the only way to deconflict competitive behaviour is to rely on random chance or on some underlying pathology of the environment to split multiple UAVs up. Increased knowledge of the partially observed environment, either through increased vision to see tasks or increased communication to tell others about tasks they have seen, leads to an increasing likelihood of converging on the same state of the world. The behavioural homogeneity of multiple agents means that similar beliefs about the state of the world will lead to similar decisions within it, resulting in an increased likelihood of UAVs converging on and competing for the same tasks. This emergent convergence property has been previously explored by the Authors in [5] for a multi-UAV surveillance problem. In particular it was shown that artificial heterogeneity, by adding small amounts of noise to an agents action choice or state observation could be used to alleviate this effect.

The results in this paper show two main ways to handle this convergence in decision making and state belief (similar to [5]). Firstly, partial observability can actually be a beneficial property of the environment, increasing the agents chances to hold differing world views allows homogeneous agents to essentially collaborate through ignorance. Secondly, and hopefully reassuringly, instead of solely relying on this ignorance, UAVs can instead model the intent of other UAVs and avoid trying to visit tasks they expect to be completed by someone else.

6. Conclusions

This paper has explored the Multi-Agent Simultaneous Searching and Routing Problem whereby multiple homogeneous UAVs are used to simultaneously search for unknown tasks in an environment and route between. A traditional global optimisation approach was modified to meet the needs of our particular problem such as decentrality and partial observability of the real world. The work is motivated by trying to mitigate competitive behaviour between UAVs who do not explicitly collaborate. In particular this paper demonstrates that collaborative behaviour can still be achieved through careful choices in parameters and simple behaviour modifications. By turning on/off two specific traits of a standard UAV type, listening to other UAVs and simple modelling of other UAVs intent, we created four distinct UAVs behaviours. Through the use of a multi-agent simulation environment we were able to simulate and investigate the parameter space of the UAVs deployed to determine optimal parameter choices to best solve the searching and routing problem.

The results of this paper demonstrate that having an improved knowledge of the environment, through seeing more tasks or being told of them by another agent, can in fact be detrimental to performance in a multi-homogeneous-agent setting. In fact, partial observability can be utilised, through limited vision and communication ranges, allowing multiple-UAVs to essentially collaborate through ignorance. Notably we show that this reliance on ignorance can be avoided if the agents do a very small amount of modelling of other agents intent. Importantly, the addition of this modelling behaviour means that increased knowledge of the world is always better.