Abstract
Delivery drones have been attracting attention as one of the promising technologies to deliver packages. Several research studies on routing problems specifically for drone delivery scenarios have extended Vehicle Routing Problems (VRPs). Most existing VRPs are based on Traveling Salesman Problems (TSPs) for minimizing the overall distance. On the other hand, VRPs for drone delivery have been aware of energy consumption due to the consideration of battery capacity. Despite hovering motions with loading packages accounting for a large portion of energy consumption since delivery drones need to hover with several packages, little research has been conducted on drone routing problems that aim at the minimization of overall flight times. In addition, flight time is strongly influenced by windy conditions such as headwinds and tailwinds. In this paper, we propose a VRP for drone delivery in which flight time is dependent on the weight of packages in a windy environment, called Flight Speed-aware Vehicle Routing Problem with Load and Wind (FSVRPLW). In this paper, flight speed changes depending on the load and wind. Specifically, a heavier package slows down flight speeds and a lighter package speeds up flight speeds. In addition, a headwind slows down flight speeds and a tailwind speed up flight speeds. We mathematically derived the problem and developed a dynamic programming algorithm to solve the problem. In the experiments, we investigate how much impact both the weight of packages and the wind have on the flight time. The experimental results indicate that taking loads and wind into account is very effective in reducing flight times. Moreover, the results of comparing the effects of load and wind indicate that flight time largely depends on the weight of packages.
1. Introduction
In recent years, drones have been expected to play an active role in a variety of fields. Drones have been employed for hobby and multimedia applications due to their high availability. In particular, package delivery services constitute a promising use of drones to solve the last-mile problem. Drone package delivery offers a variety of advantages over conventional deliveries. Since drones deliver packages in flight, they are not affected by traffic jams or other road conditions. They also emit less CO2 since they are battery powered, and their unmanned flight reduces labor costs required for the delivery. Kirschstein et al. [1] have researched the usefulness of delivery drones in terms of energy consumption. This study indicated that delivery drones are superior to vehicle deliveries. Since drones are unmanned, it is clear that labor costs can be reduced compared to vehicle package delivery. Many companies have been taking advantage and have started logistic businesses [2,3]. Therefore, drone delivery, especially for finding an efficient delivery route, has been extensively investigated for a decade [4,5,6,7].
Drone package delivery is derived initially from Traveling Salesman Problems (TSP) [8]. As one of the extensions, Vehicle Routing Problems (VRPs) have been developed to take into account the features of vehicles. VRPs have classically targeted routing problems for trucks; therefore, the characteristics specialized for drones have not been assumed in the problems. Dorling et al. investigated a vehicle routing problem for drones [9]. A variety of extensions of VRPs for drone delivery has been developed. Many researchers focused on energy consumed on drones since most of the drones are powered by a battery and can hardly fly for a long period of time. Unfortunately, each of the energy models presented in research studies is available only for a specific drone; therefore, the proposals do not address the issue that energy models are required for diverse drones. In terms of energy consumption, the flight time that includes hover time and transport time is one of the crucial perspectives since hovering with loading packages accounts for a large portion of energy consumption on drones [10]. Regardless of this fact, most of the extensions for drone delivery have assumed that flight speed is fixed. For drone delivery, the drone has to carry packages and make changes to flight speeds depending on the weight of the packages. Funabashi et al. [11] proposed a delivery plan that takes into account the change in flight speed due to loads. Furthermore, flight is affected by weather environments. Significant interference represents windy conditions where tailwind speeds up the drone, while headwind slows it down. Ito et al., Luo et al., and Guerrero et al. [12,13,14] presented VRPs for drone delivery that take into account the windy effect. Unfortunately, however, such research studies did not assume that the weight of packages affects the flight speed of drones.
In this paper, we propose a VRP for drone delivery, which assumes that the flight speed is affected by the weight of packages and windy environment, and we attempt to minimize the overall flight time. In general, the drone routing problem covers a range of flight speeds from 0 to 23 m/s and a maximum payload of 25 kg [15]. The payload depends on drone size. This paper is an extended version of [11], and the extensions are addressed as follows. In the paper of [11], the weight of packages is assumed to affect flight speeds. However, the windy condition is indispensable in order to determine the routing order. Our proposed VRP, called Flight Speed-aware Vehicle Routing Problem with Load and Wind (FSVRPLW), considers both the weight of packages and the windy condition in order to pursue the primary factor that largely depends on the overall flight time. In the conventional drone routing problem, the flight speed of the drone is considered to be constant. However, the flight speed of a drone varies depending on the load and wind. We focus on this and propose a new problem. In this problem, we assume that flight speed changes with the load and wind. Specifically, when the payload is heavy, the flight speed becomes slow. On the other hand, when the payload is light, the flight speed becomes fast. In addition, when the drone flies in a headwind, the flight speed becomes slow. On the other hand, when the drone flies with a tailwind, the flight speed becomes fast. We mathematically derived FSVRPLW for drone delivery and also proposed an algorithm to solve the problem based on dynamic programming. Furthermore, we evaluate the scalability of our algorithms for the number of customers available for drone delivery throughout runtime evaluation. Given a set of packages to deliver and wind, FSVRPLW tries to find an optimal route that starts from a depot, delivers all of the packages to customers, and comes back to the depot with the effect of wind in mind. Our dynamic programming algorithm efficiently finds an optimal route such that the overall flight time is minimized.
2. Related Works
In recent years, many approaches for drone delivery have been extensively surveyed [4,5,6,7]. Drone delivery planning has been specially investigated as the extension of TSPs [16,17,18,19,20]. Agatz et al. [16] have proposed a flight side-kick routing problem that determines the delivery order using both drones and trucks. In addition, Bouman et al. [17] have introduced a dynamic programming algorithm to solve the delivery planning problem using trucks and drones. The studies in [16,17] do not consider the wait time after the truck or drone finish each of the deliveries. In Marinelli et al. and Ha et al. [18,19], the proposed problems are aimed to minimize the wait time of trucks and drones and the battery consumption of drones. Murray et al. [20] have proposed a problem where the drone is assumed to depart from a truck. Tu et al., Kitjacharoenchai et al., Saleuet et al., and Ham et al. [21,22,23,24] further extended the drone delivery problem for using multiple drones and trucks. Ham et al. [24] addressed a problem where drones not only deliver but also collect packages. These research studies have assumed that drones and trucks perform only one delivery, but Ham et al. [24] considered the collection. However, most of the research studies have had simple assumptions for routing. In other words, TSP-based problems do not take into account the unique properties of vehicles. In particular, for drones, flight speeds and times often change largely depending on the load, battery condition, and natural environments. Therefore, TSP-based routing problems are insufficient for obtaining a practical route.
As one of the extensions for TSPs, VRP-based problems, which consider the characteristics of vehicles, have been developed for pursuing a practical routing solution. Unlike TSPs, VRPs are aimed at the minimization of energy consumption, delivery time, and travel distance by considering the characteristics of the vehicles. Specific to drones, the significant perspective is to reduce the total cost of the delivery flight. There are several studies that consider delivery costs involved in delivering by truck or drone in Poikonen et al., Wang et al., and Minh et al. [25,26,27].
The minimization of energy consumption is set as the major cost in drone-based delivery to avoid crashing. Therefore, Energy Minimizing Vehicle Routing Problems (EMVRPs) have been developed in Ito et al., Kara et al., and Funabashi et al. [12,28,29]. In general, the energy consumption of a drone is accounted for by the most significant hover portion. The evidence is referred to by research in [10,30], where the authors have measured the energy consumption of an AR Drone 2.0 with a variety of flight speeds and weight of loads. In these studies, the flight speed of the drone is less than 6 m/s and the load is up to 168 g. The experimental results of these studies show that flight speed depends on the weight of loads, and flight speed largely affects energy consumption. From this perspective, several research studies that consider variable flight speeds and flight times have been proposed. Dorling et al. [9] proposed a delivery plan that considers the impact on energy consumption and flight times by weights of loads and a battery. However, Poikonen et al., Wang et al., and Ha et al. [25,26,27] assumed constant flight speeds even if the drones loaded packages. On the other hand, a drone routing problem, which is called Flight Speed-aware Vehicle Routing Problem (FSVRP), that takes into account flight speeds depending on loads has been proposed in [11]. In the literature [11], changes in flight speed due to loading are taken into account. Specifically, the heavier the load on the drone, the slower the flight speed becomes. Conversely, if the load on the drone is light, flight speed becomes faster. Research assumed that lift power is constant and the flight speed of the drone is dependent on the payload. The reduction in the total flight time results in a reduction in total energy consumption. It can be observed that Funabashi et al. [11] results in reducing total energy consumption. Unfortunately, in the real world, flight speed is not only affected by loads but also affected in a windy environment. There has been little research that takes into account wind, which affects the flight speed of a drone [12,13,14]. Ito et al., Funabashi et al., and Bouman et al. [11,12,17] proposed a fast method for solving the problem by using dynamic programming proposed for the drone routing problem. Moreover, a genetic algorithm is used as a fast method to solve this problem. Several research studies used the genetic algorithm, a form of artificial intelligence, for delivery drone routing problem [27,31,32]. However, both load and wind-aware routing problems for drone delivery have not yet appeared. To the best of our knowledge, this is the first research study that considers both load and wind that affect the overall flight time.
3. A Description of FSVRPLW
Our proposal is an extension of FSVRP, which was proposed by Funabashi et al. [11]. However, unlike FSVRP, our proposed problem considers both the weight of the load and windy conditions; therefore, we call the problem a Flight Speed-aware Vehicle Routing Problem with Load and Wind (FSVRPLW). In the following section, we present a motivating example to show the significance of this problem and mathematically derive the problem.
3.1. A Motivational Example
Figure 1 shows an example of the problem in this paper. This figure represents the distance between customers and the weight of the package to be delivered to each customer in the case that the number of customers is three. The unit of weight of the package is g, and wind speed is assumed to be blowing at 2 m/s in a constant direction. It is also assumed that the speed of the drone is 5 m/s.
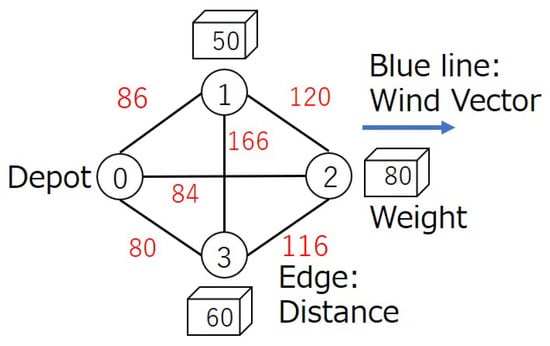
Figure 1.
An example problem.
Each node represents a customer, the edge represents the flight distance, and the square box represents the weights of the packages to be delivered to each customer. Node 0 represents the depot. For example, when transporting a package from the depot to customer 2, the weight of the package is 80, and flight distance is 84. Note that the example assumes that wind blows in the direction from the depot towards customer 2.
FSVRP changes its flight speed depending on the weight of loads. If the packages are heavy, flight speed becomes slow. In contrast, the drone can fly fast if packages are light. In terms of the characteristic, a heavy package is intuitively delivered first to minimize the overall flight time. However, windy interference can slow down the flight of the drone and cannot be negligible.
Figure 2a,c show the optimal path in FSVRP. Figure 2a shows the flight distance in FSVRP, and Figure 2c shows flight times. Figure 2b,d show the optimal path in FSVRPLW. Figure 2b shows the flight distance in FSVRPLW, and Figure 2d shows the flight time. The flight time shown in these figures is the flight time when the flight speed changes due to load and wind. The detail of how to calculate the flight time is addressed in Section 3.2 and Section 3.3. In Figure 2a–d, the delivery order drawn in red lines is found so that the overall flight time in the FSVRP is minimized. The flight time of the drone is derived from the overall flight distance and the weight of the loads.
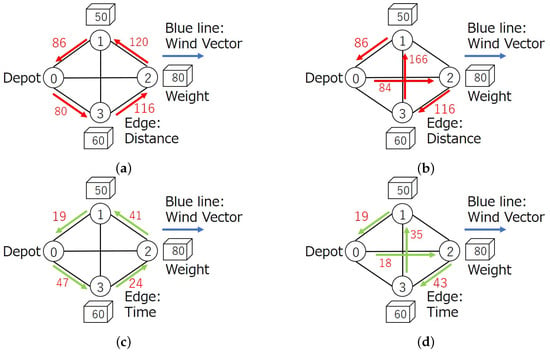
Figure 2.
Comparison of FSVRP and FSVRPLW: (a) flight distance of FSVRP, (b) flight distance of FSVRPLW, (c) flight time of FSVRP, and (d) flight time of FSVRPLW.
Recall that the heavier the load, the slower flight speed becomes, resulting in longer flight times. This fact intuitively implies that heavier packages are given priority for delivery. However, the optimal solution opposes intuition since not only the weight of packages but also flight distance is important for minimizing flight times. In the result of FSVRP, the overall flight distance for FSVRP represents , and flight time represents . FSVRPLW additionally considers the windy effect to determine the delivery route. The optimal route in FSVRPLW is shown in Figure 2b,d. In the example, tailwind from the depot to customer 2 helps the flight, and the first visit represents customer 2 in the result of FSVRPLW. Therefore, the optimal flight distance for FSVRPLW is , and flight time is .
This example shows that a drone flies different paths in FSVRP and FSVRPLW. FSVRP can result in a route that reduces flight time by prioritizing customers with heavy loads and close flight distances. Therefore, in the example, the first delivery is to customer 3, who requires a heavy load and a short flight distance. On the other hand, FSVRPLW can shorten the total flight time by taking advantage of windy conditions. In the example, the package is first delivered to customer 2, to whom the drone can fast fly to even if it carries the heaviest package. In FSVRPLW, flight time is reduced regardless of the long flight distance.
3.2. FSVRPLW Formulation
This section describes the formulations of FSVRP and FSVRPLW.
We are given N packages to deliver. In order to avoid lost generality, we do not deliver more than two packages to the same customer, and the number of customers is also N. In other words, multiple packages to the same customer are combined in advance. In this paper, we assume that packages can be delivered in a single trip; therefore, it does not require multiple trips. In addition, in a single trip, multiple visits to a customer must result in a loss of energy consumption and flight time. The customer to whom package i is delivered is called customer i, and the depot is numbered 0, as shown in the example in Figure 1. In this paper, we assume that all packages are delivered at one time. This means that all packages are loaded onto the drone at the depot, and then the delivery is started. The packages need to be divided for another tour if the total weight of the packages exceeds the carrying capacity of the drone, but this is out of the scope of this paper. Let denote the distance between customers and . Moreover, let denote the j-th visited customer, which is the decision variable of the routing problem. Since a route starts and ends at the depot, we define the following.
Moreover, all customers are visited once, which is formally defined as follows.
Let denote the weight of package i, and is the weight of the drone itself. Let the total load when the drone departs the j-th customer. When the drone starts a delivery, all packages are loaded. Therefore, the following equation is valid.
When the drone makes the j-th stop at customer , a package of weight is unloaded. Therefore, the total load when the drone leaves customer is defined as follows:
Let denote the flight time between customer and . Then, the drone flight time from to is given by the distance between and divided by the drone flight speed. Note that is a function of load. Therefore, the flight time between customers j-th visited and -th visited is defined as follows.
FSVRP asks for the shortest flight time in all flight routes, and its objective function is defined as follows.
The FSVRPLW addressed in this paper is formally defined as follows. Given w, d, and v, find x, which minimizes the objective function (7) while meeting constraints (1)–(6).
In FSVRPLW, the effect of wind is added to the velocity used in FSVRP. Let be the flight speed of the drone that takes into account the effects of wind and load. is a function of the load, wind speed, and the position vector of the customer. If the speed of the drone is , the speed of the wind is , and the position vector of the customer to is . Equation (6) is defined as follows.
Therefore, FSVRPLW asks the shortest flight time in all flight routes, and its objective function is defined as follows.
3.3. Effects on Flight Speed of a Drone
Function of the drone’s flight speed in the previous section varies depending on the drone model. In this study, is assumed to be given, and an example of calculating is shown below. First, the effect of load on the flight speed of the drone is described.
Figure 3a,b show the effects of load on flight speed. These figures show the situation when the drone is viewed from the side. Figure 3a shows the drone when it is not carrying a load. P represents the lift force and represents the pitch angle of the drone. Moreover, represents the weight of the drone itself. The drone should not fall. Therefore, the vertical component of P, i.e., , must be equal to gravity force . Let denote the pitch angle where is equal to the gravity.
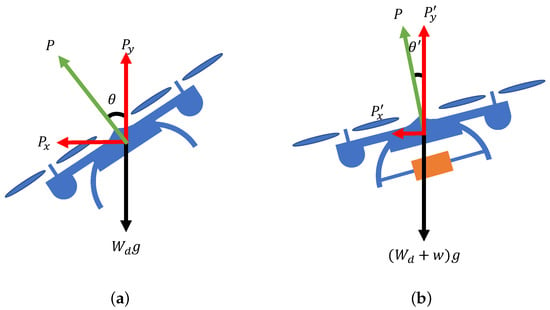
Figure 3.
Effect of load: (a) drone without load and (b) drone with load w.
The horizontal component of P, i.e., , is the power towards the destination, and it is assumed to be equal to air resistance , where k is a drone-specific coefficient.
Figure 3b shows a flying drone with load w. In order not to fall down, pitch angle must be smaller than . Then, we derive the following formulas.
Hence, we derive the following.
Therefore, the flight speed of the drone when the drone is loaded with a load is as follows.
Next, we consider the effect of the wind in the direction of travel of the drone. Specifically, if the wind is blowing in the opposite direction to the drone’s direction of travel, the drone’s flight speed will decrease under the influence of the wind. In other words, flight speed will decrease due to wind speed. However, the wind may not only slow down the drone’s flight speed but may also speed it up. If the wind is blowing in the same direction as the drone’s direction of travel, the drone’s flight speed will increase under the influence of the wind. The flight speed of a drone varies greatly under the influence of wind. In this study, wind speed is assumed to be slower than the drone’s maximum speed without wind. Otherwise, the drone may not reach customers.
Velocity change due to wind is represented using vector calculations. Figure 4 shows that the wind is blowing in a specific direction relative to the drone. In this figure, wind is blowing as the drone moves from customer to customer . Let denote the angle between the customer vector and the wind vector . Moreover, let denote the flight speed of the drone. The angle between the drone’s flight speed , and customer vector needs to be calculated.
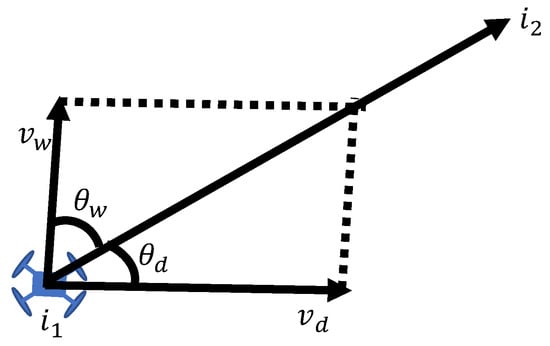
Figure 4.
Drone flight under windy conditions.
Figure 5 shows the change in flight speed due to wind. Let be the flight speed of the drone considering the effect of wind. The flight speed considering the effect of wind requires that the direction of the composite vector of the drone’s flight speed and wind speed matches the direction of the customer vector . If the angle between and is , then || is define as follows.
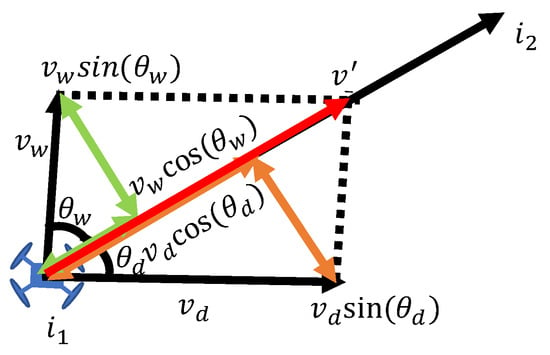
Figure 5.
Speed changed by wind.
Therefore, is derived as follows.
The norm of synthetic vector of and can be expressed as follows.
4. A Dynamic Programming Algorithm
In this section, we propose an algorithm to rapidly solve FSVRPLW, which is presented in the previous section. FSVRPLW is one of the NP-hard problems since the problem is based initially on TSP. If the problem is implemented with a brute-force search algorithm, the complexity of this problem indicates , and the algorithm can hardly solve a large size of problems in a practical time. In this paper, we present a dynamic programming algorithm to solve FSVRPLW [33]. Dynamic programming algorithms recursively divide a problem into subproblems and uses an optimal solution of the subproblem to globally find the optimal solution all over the problem. Dynamic programming algorithm is efficient in that it does not recalculate the same subproblem.
Let denote a set of customers already visited and i denote the last customer visited in a set of . We also call a state. Denote the initial state as . Then, the minimum flight time spent during the delivery from initial state to state is denoted as . Here, the asymptotic equation for calculating can be derived as follows.
Now, we address the detail of the presented equation. Let i be the last customer visited in , and let represent the second-to-last customer visited in . represents the minimum flight time to travel from the depot to , and represents the flight time to fly from customer to customer i. The flight time during moving from customer to customer i takes into account the weight of the package and the effect of wind. The initial state is represented as . Here, represents the flight time before departing from the depot. Note that the flight time before departure from the delivery base is zero. Therefore, can be expressed as follows.
In addition, the routing problem asks for the route that minimizes the overall flight time, starting at the depot, visiting all customers, and returning to the depot. Therefore, if the number of customers is assumed to be N, the routing problem is formally defined as follows.
The problem represented as Equation (24) is recursively divided into subproblems according to Equation (22). If the divided subproblems reach Equation (23), the optimal delivery route in which flight time is minimized is obtained.
Algorithm 1 is a pseudo-code based on dynamic programming. represents the total payload to be delivered, and represents the set of customers. represents the set of customers who have already visited. The inputs to the drone routing problem in this paper are the number of customers, the payload of each customer’s package, the coordinates of each customer, and wind velocity. The output is the delivery route with the shortest total flight time. Here, is a bit vector of length N, where N is the number of customers. Therefore, when customer i is visited, the -th bit is set. For example, suppose the number of customers is 4, and customer 2 has already been visited. In this case, Visited can be expressed as in binary. In this manner, is expressed by setting up the bit of the customers who have been visited. is a two-dimensional array that stores the flight time, corresponding to . For example, indicates that customer 2 and customer 3 have already been visited, and the drone is currently at customer 3. Next, we will explain the processing performed in each line of the pseudo-code. Line 1 stores the sum of the payloads given in the input in . Lines 3–6 calculate the flight time from the depot to each customer and store the results in array . In addition, the total weight of the package carried by the drone is stored in the array since flight speed varies with load and wind in this paper. Next, in lines 8–20, we calculate the flight time when all remaining customers are moved. Finally, in lines 23–25, the flight time from the last customer to the delivery location is calculated. In addition, the flight time of the route that minimizes the total flight time is stored in . Lines 8–20 are the most important part of the dynamic programming algorithm and play an active role in reducing calculation times. In a dynamic programming algorithm, instead of recursive procedural calls, flight time is calculated in a three-level nested loop. The computational complexity of the dynamic programming algorithm used in this study is . It is much faster than , which is the computational complexity of the full search algorithm.
| Algorithm 1 Dynamic Programming Algorithm for FSVRPLW. |
| Input: N: Number of customer, W: Payload of each customer, C: Coordinates of each customer, : Wind Vector Output: Optimal Route: The route that minimizes the total flight time
|
5. Evaluation
The effectiveness of our proposed FSVRPLW is evaluated by conducting experiments. We implemented several routing algorithms in Python, and they are compared in terms of total flight distance, the total flight time, and the runtime of the algorithms.
5.1. Experimental Setup
Five routing algorithms shown below are compared in the experiments:
- DPTSP: Dynamic programming algorithm for TSP. The route that minimizes the flight time is calculated. However, it does not take into account wind and load.
- DPFS-L: Dynamic programming algorithm for FSVRP [11]. The route that minimizes the flight time is calculated. It takes into account only load.
- DPFS-W: Dynamic programming algorithm for FSVRPLW. The route that minimizes flight time is calculated. It takes into account only wind.
- BFFS-LW: A brute-force algorithm for FSVRPLW. It exhaustively explores all possible routes (i.e., N! routes) to find the one with minimum flight times.
- DPFS-LW: Our DP algorithm proposed in Section 4 for FSVRPLW. This algorithm is the proposed method.
In the experiments, the number of customers changed from 5 to 20. For each number of customers, we randomly created 20 problem instances with different customers’ locations, weights of packages, wind directions, and wind speeds. Therefore, we created a total of 320 problem instances. Then, we evaluated five routing algorithms in terms of flight time, flight distance, and algorithm runtime. AR. Drone 2.0 was referenced for the calculated delivery drone problem. The reason why we used AR. Drone 2.0 in this study is that our research group has been conducting studies on the AR. Drone 2.0. Therefore, we were able to set parameters based on our knowledge. However, the proposed method does not depend on the type of drone; thus, other drones can be applied to the proposed method. The speed of the drone is set to 5 m/s when it is not carrying a load. The drone weight is assumed to be 490 g. The load capacity of the drone is assumed to be 200 g; therefore, the total weight of packages carried at once is within 200 g. Wind speed is set to be 2 m/s in a constant direction. The wind speed was set to the speed at which the drone can fly even when it is loaded with the maximum payload. This paper uses the AR. Drone model as an example of a drone. However, the drones that can be adapted in this paper are not limited to the AR. Drone. It is possible to use a larger drone to carry a larger load. In our preliminary experiments, the AR. Drone was able to carry a load of less than 200 g. Packages weighing less than 200 g include documents and mail. We set the runtime limit up to 3600 s.
5.2. Experimental Results
Figure 6 represents the results of the five methods in terms of flight time. The vertical axis shows the flight time when each method is normalized by DPFS-LW. As described above, there are 20 problem instances for each number of customers. Therefore, each bar in the graph denotes the average flight time among 20 problem instances. The horizontal axis shows the number of customers. BFFS-LW and DPFS-LW show the same results until the number of customers is 11. This shows that both the brute-force search algorithm and the dynamic programming algorithm can find the solution. The results of BFFS-LW are not shown since calculation time exceeds one hour after the number of customers is 12. The proposed method, DPFS-LW, has the shortest flight time in all results. Comparing DPFS-L and DPFS-LW, the flight time of DPFS-LW decreased by 5.10% on average. Moreover, by comparing DPTSP and DPFS-LW, the flight time of DPFS-LW decreased by 18.46% on average. The average difference between DPTSP and DPFS-W is 1.98%. On the other hand, the average difference between DPTSP and DPFS-L is 13.35%. The difference is larger than that in the case of flight distance. Therefore, it can be observed that wind has some effect on flight time. Although DPTSP does not take into account loads and winds, DPTSP does not have the maximum flight time in all results. DPTSP does not necessarily have the longest flight time due to the existence of multiple solutions.
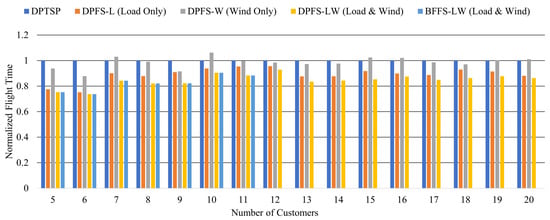
Figure 6.
Comparison of flight time.
Next, Figure 7 shows the result of the five methods in terms of flight distance. The vertical axis shows the flight distance when each method is normalized by DPFS-LW. The horizontal axis shows the number of customers. BFFS-LW and DPFS-LW show the same results until the number of customers is 11. This shows that both the brute-force search algorithm and the dynamic programming algorithm can find the solution. The results of BFFS-LW are not shown since the calculation time exceeds one hour more than 12 customers. The proposed method, DPFS-LW, has the longest flight distance in all results. Comparing DPFS-L and DPFS-LW, the flight distance of DPFS-LW increased by 1.43% on average. It is believed that flight distance is increased due to the use of wind in flight compared to the prior method. DPTSP has the shortest flight distance in all results. Comparing DPTSP and DPFS-LW, the flight distance of DPTSP is shorter by 2.42% on average. The flight distances of DPTSP and DPFS-W are very close to each other. The average difference between DPTSP and DPFS-W is 0.18%. On the other hand, the average difference between DPTSP and DPFS-L is 1.00%. This indicates that the wind does not have a significant effect on flight distance.
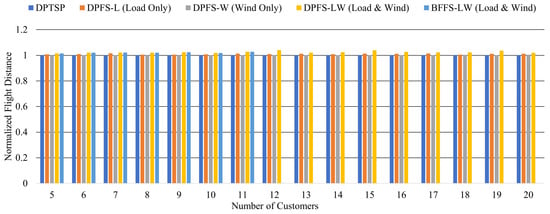
Figure 7.
Comparison of flight distance.
The results show that our proposed DPFS-LW increases flight distance but decreases flight time. This is due to the use of wind and load, which can deliver the package more efficiently. These results show that it is important to consider speed variations due to load and wind in drone delivery.
In this paper, the wind is assumed to be constantly blowing in terms of direction and speed, but wind dynamically changes. In this paper, we simplify the wind model to evaluate how the flight time changes by whether the wind is considered or not. Undoubtedly, the effect of wind on the drone may change due to various factors. Therefore, it is necessary to verify the effect of wind on the drone in more detail, which is considered in one of our future works.
Next, Figure 8 shows the runtime of each method by using a logarithmic scale. The vertical axis shows runtime, and the horizontal axis shows the number of customers. The methods mentioned except for BFFS-LW can find a solution within one hour. This result shows that our proposed algorithm can be useful even when there are 20 customers.
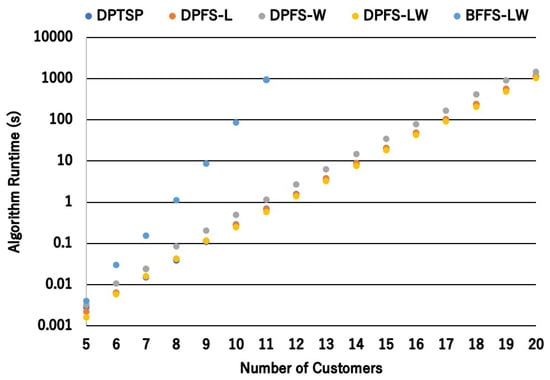
Figure 8.
Algorithm runtime.
6. Conclusions
Drones are expected to be popular vehicles for delivery services. In this paper, we formulated FSVRPLW, which is an extension of FSVRP. The problem determines an optimal route such that the total flight time is minimized by taking into account the weight of load and wind effects that affect the flight speed of a drone. In order to effectively solve the problem, we also proposed a dynamic programming algorithm. Experimental results show the effectiveness of the proposed algorithm. In future work, we will consider dynamically changing windy conditions and package division for multiple tours.
Author Contributions
Conceptualization, S.I. and K.A.; methodology, S.I., Y.F. and H.N.; software, S.I., K.A. and H.N.; validation, S.I.; formal analysis, S.I. and H.N.; data curation, S.I.; resources, H.N., X.K. and H.T.; investigation, S.I., Y.F. and H.N.; visualization, S.I.; writing—original draft preparation, S.I.; writing—review and editing, S.I., H.N., X.K. and H.T.; supervision, H.T.; project administration, X.K., I.T. and H.T.; funding acquisition, H.N., X.K. and H.T. All authors have read and agreed to the published version of the manuscript.
Funding
This work is in part supported by KAKENHI 20H04160 and 20J21208.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare that they have no conflicts of interest regarding the publication of this paper.
References
- Kirschstein, T. Comparison of Energy Demands of Drone-based and Ground-based Parcel Delivery Services. Transp. Res. Part D Transp. Environ. 2020, 78, 102209. [Google Scholar] [CrossRef]
- Amazon Prime Air. Available online: www.amazon.com/b?node=8037720011 (accessed on 22 October 2021).
- Project Wing. Available online: https://x.company/projects/wing/ (accessed on 22 October 2021).
- Viloria, D.R.; Solano-Charris, E.L.; Muñoz-Villamizar, A.; Montoya-Torres, J.R. Unmanned Aerial Vehicles/Drones in Vehicle Routing Problems: A Literature Review. Int. Trans. Oper. Res. 2021, 28, 1626–1657. [Google Scholar] [CrossRef]
- Macrina, G.; Pugliese, L.D.P.; Guerriero, F.; Laporte, G. Drone-aided Routing: A Literature Review. Transp. Res. Part C Emerg. Technol. 2020, 120, 102762. [Google Scholar] [CrossRef]
- Chung, S.H.; Sah, B.; Lee, J. Optimization for Drone and Drone-truck Combined Operations: A Review of the State of the Art and Future Directions. Comput. Oper. Res. 2020, 123, 105004. [Google Scholar] [CrossRef]
- Khoufi, I.; Laouiti, A.; Adjih, C. A Survey of Recent Extended Variants of the Traveling Salesman and Vehicle Routing Problems for Unmanned Aerial Vehicles. Drones 2019, 3, 66. [Google Scholar] [CrossRef] [Green Version]
- Applegate, D.L.; Bixby, R.E.; Chvátal, V.; Cook, W.J. The Traveling Salesman Problem; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Dorling, K.; Heinrichs, J.; Messier, G.G.; Magierowski, S. Vehicle Routing Problems for Drone Delivery. IEEE Trans. Syst. Man Cybern. Syst. 2016, 47, 70–85. [Google Scholar] [CrossRef] [Green Version]
- Ito, S.; Negoro, S.; Kong, X.; Taniguchi, I.; Tomiyama, H. A Methodology for Measuring Flight Speed of Drones in Indoor Environments. Procedia Comput. Sci. 2021, 187, 322–328. [Google Scholar] [CrossRef]
- Funabashi, Y.; Taniguchi, I.; Tomiyama, H. Work-in-Progress: Routing of Delivery Drones with Load-Dependent Flight Speed. In Proceedings of the 2019 IEEE Real-Time Systems Symposium (RTSS), Hong Kong, China, 3–6 December 2019; pp. 520–523. [Google Scholar]
- Ito, S.; Nishikawa, H.; Kong, X.; Funabashi, Y.; Shibata, A.; Negoro, S.; Taniguchi, I.; Tomiyama, H. Energy-aware Routing of Delivery Drones under Windy Conditions. IPSJ Trans. Syst. Lsi Des. Methodol. 2021, 14, 30–39. [Google Scholar] [CrossRef]
- Luo, H.; Liang, Z.; Zhu, M.; Hu, X.; Wang, G. Integrated Optimization of Unmanned Aerial Vehicle Task Allocation and Path Planning Under Steady Wind. PLoS ONE 2018, 13, e0194690. [Google Scholar] [CrossRef] [Green Version]
- Guerrero, J.A.; Bestaoui, Y. UAV Path Planning for Structure Inspection in Windy Environments. J. Intell. Robot. Syst. 2013, 69, 297–311. [Google Scholar] [CrossRef]
- Zhang, J.; Campbell, J.F.; Sweeney, D.C., II; Hupman, A.C. Energy consumption models for delivery drones: A comparison and assessment. Transp. Res. Part D Transp. Environ. 2021, 90, 102668. [Google Scholar] [CrossRef]
- Agatz, N.; Bouman, P.; Schmidt, M. Optimization Approaches for the Traveling Salesman Problem with Drone. Transp. Sci. 2018, 52, 965–981. [Google Scholar] [CrossRef]
- Bouman, P.; Agatz, N.; Schmidt, M. Dynamic Programming Approaches for the Traveling Salesman Problem with Drone. Networks 2018, 72, 528–542. [Google Scholar] [CrossRef] [Green Version]
- Marinelli, M.; Caggiani, L.; Ottomanelli, M.; Dell’Orco, M. En Route Truck–drone Parcel Delivery for Optimal Vehicle Routing Strategies. IET Intell. Transp. Syst. 2018, 12, 253–261. [Google Scholar] [CrossRef]
- Ha, Q.M.; Deville, Y.; Pham, Q.D.; Hoàng Hà, M. On the Min-cost Traveling Salesman Problem with Drone. Transp. Res. Part C Emerg. Technol. 2018, 86, 597–621. [Google Scholar] [CrossRef] [Green Version]
- Murray, C.C.; Chu, A.G. The Flying Sidekick Traveling Salesman Problem: Optimization of Drone-assisted Parcel Delivery. Transp. Res. Part C Emerg. Technol. 2015, 54, 86–109. [Google Scholar] [CrossRef]
- Tu, P.A.; Dat, N.T.; Dung, P.Q. Traveling Salesman Problem with Multiple Drones. In Proceedings of the Ninth International Symposium on Information and Communication Technology, Danang City, Vietnam, 6–7 December 2018; pp. 46–53. [Google Scholar]
- Kitjacharoenchai, P.; Ventresca, M.; Moshref-Javadi, M.; Lee, S.; Tanchoco, J.M.A.; Brunese, P.A. Multiple Traveling Salesman Problem with Drones: Mathematical Model and Heuristic Approach. Comput. Ind. Eng. 2019, 129, 14–30. [Google Scholar] [CrossRef]
- Saleu, R.M.; Deroussi, L.; Feillet, D.; Grangeon, N.; Quilliot, A. An Iterative Two-step Heuristic for the Parallel Drone Scheduling Traveling Salesman Problem. Networks 2018, 72, 459–474. [Google Scholar] [CrossRef]
- Ham, A.M. Integrated Scheduling of M-truck, M-drone, and M-depot Constrained by Time-window, Drop-pickup, and M-visit Using Constraint Programming. Transp. Res. Part C Emerg. Technol. 2018, 91, 1–14. [Google Scholar] [CrossRef]
- Poikonen, S.; Wang, X.; Golden, B. The Vehicle Routing Problem with Drones: Extended Models and Connections. Networks 2017, 70, 34–43. [Google Scholar] [CrossRef]
- Wang, Z.; Sheu, J.-B. Vehicle Routing Problem with Drones. Transp. Res. Part B Methodol. 2019, 122, 350–364. [Google Scholar] [CrossRef]
- Ha, Q.M.; Deville, Y.; Pham, Q.D.; Hoàng Hà, M. A Hybrid Genetic Algorithm for the Traveling Salesman Problem with Drone. J. Heuristics 2020, 26, 219–247. [Google Scholar] [CrossRef] [Green Version]
- Kara, I.; Kara, B.Y.; Yetis, M.K. Energy Minimizing Vehicle Routing Problem. In Proceedings of the International Conference on Combinatorial Optimization and Applications, Xi’an, China, 14–16 August 2007; pp. 62–71. [Google Scholar]
- Funabashi, Y.; Shibata, A.; Negoro, S.; Taniguchi, I.; Tomiyama, H. A Dynamic Programming Algorithm for Energy-aware Routing of Delivery Drones. In Advances in Artificial Intelligence and Data Engineering; Springer: Singapore, 2021; pp. 1217–1226. [Google Scholar]
- Ito, S.; Negoro, S.; Kong, X.; Taniguchi, I.; Tomiyama, H. Improved Modeling of Energy Consumption of Delivery Drones. In Proceedings of the Workshop on Synthesis And System Integration of Mixed Information Technologies (SASIMI), Online, 29–30 March 2021; pp. 56–60. [Google Scholar]
- Shivgan, R.; Dong, Z. Energy-Efficient Drone Coverage Path Planning using Genetic Algorithm. In Proceedings of the IEEE International Conference on High Performance Switching and Routing (HPSR), Newark, NJ, USA, 11–14 May 2020; pp. 1–6. [Google Scholar]
- Peng, K.; Du, J.; Lu, F.; Sun, Q.; Dong, Y.; Zhou, P.; Hu, M. A Hybrid Genetic Algorithm on Routing and Scheduling for Vehicle-assisted Multi-drone Parcel Delivery. IEEE Access 2019, 7, 49191–49200. [Google Scholar] [CrossRef]
- Held, M.; Karp, R.M. A Dynamic Programming Approach to Sequencing Problems. J. Soc. Ind. Appl. Math. 1962, 10, 196–210. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).