Mapping the Leaf Area Index of Castanea sativa Miller Using UAV-Based Multispectral and Geometrical Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area Characterization and Field Measurements
2.2. Multispectral Data Acquisition from Unmanned Aerial Vehicles
2.3. Data Processing
2.3.1. Photogrammetric Processing
| Vegetation Index | Equation | Reference |
|---|---|---|
| Normalized Difference Vegetation Index | [66] | |
| Green Normalized Difference Vegetation Index | [67] | |
| Green Red Vegetation Index | [68] | |
| Normalized Difference Red Edge | [69] | |
| Soil Adjusted Vegetation Index | [70] | |
| Renormalized Difference Vegetation Index | [71] | |
| Ratio Vegetation Index | [72] | |
| Normalized Difference Excess Near Infrared | [61] | |
| Normalized Difference Excess Red Edge | [61] |
2.3.2. Individual Tree Crown Detection and Parameter Extraction
2.4. Data Analysis
3. Results
3.1. Data Characterization
3.2. Tree Height and Crown Diameter Estimation
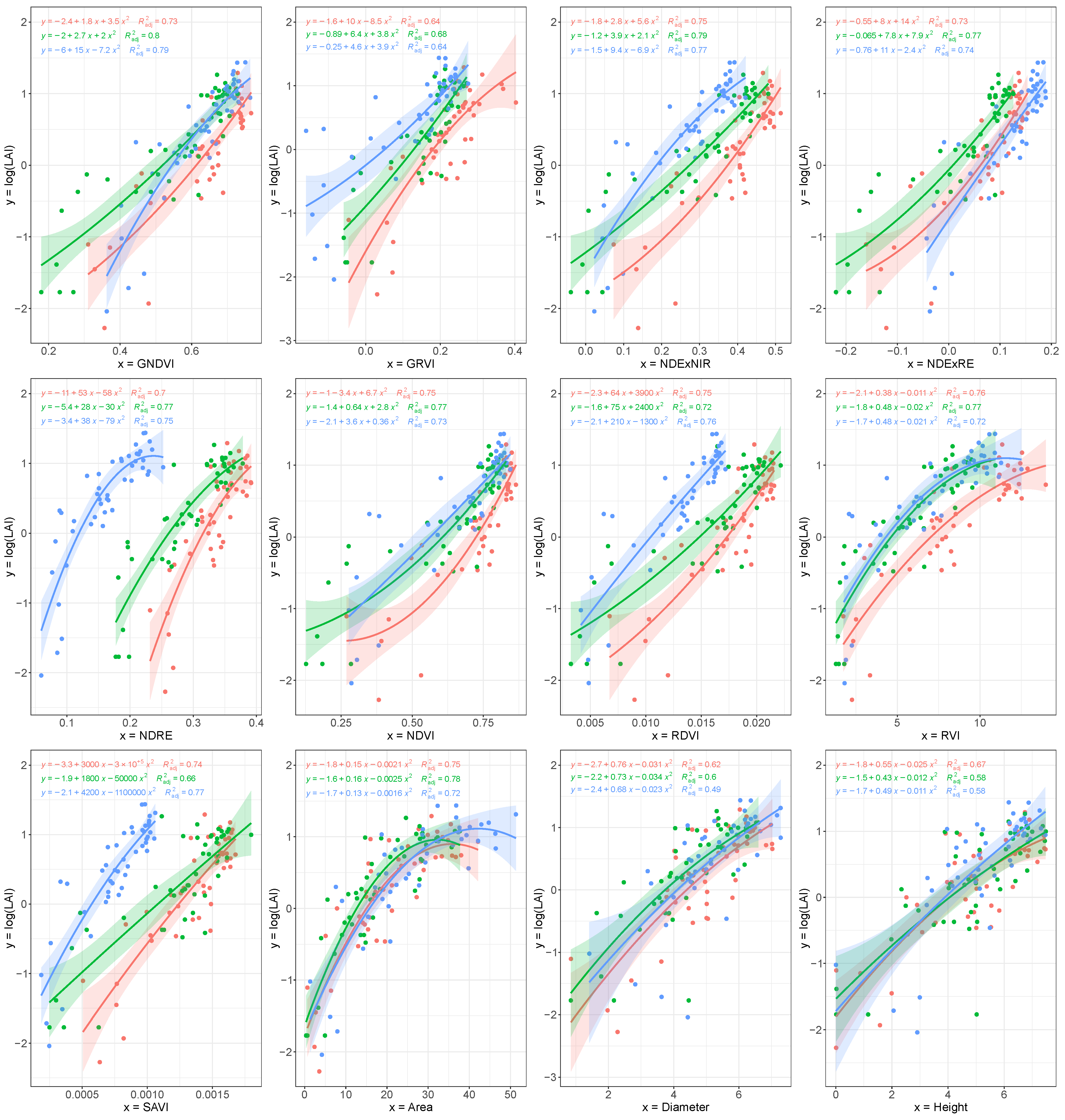
3.3. Leaf Area Index: Single Variable Correlation
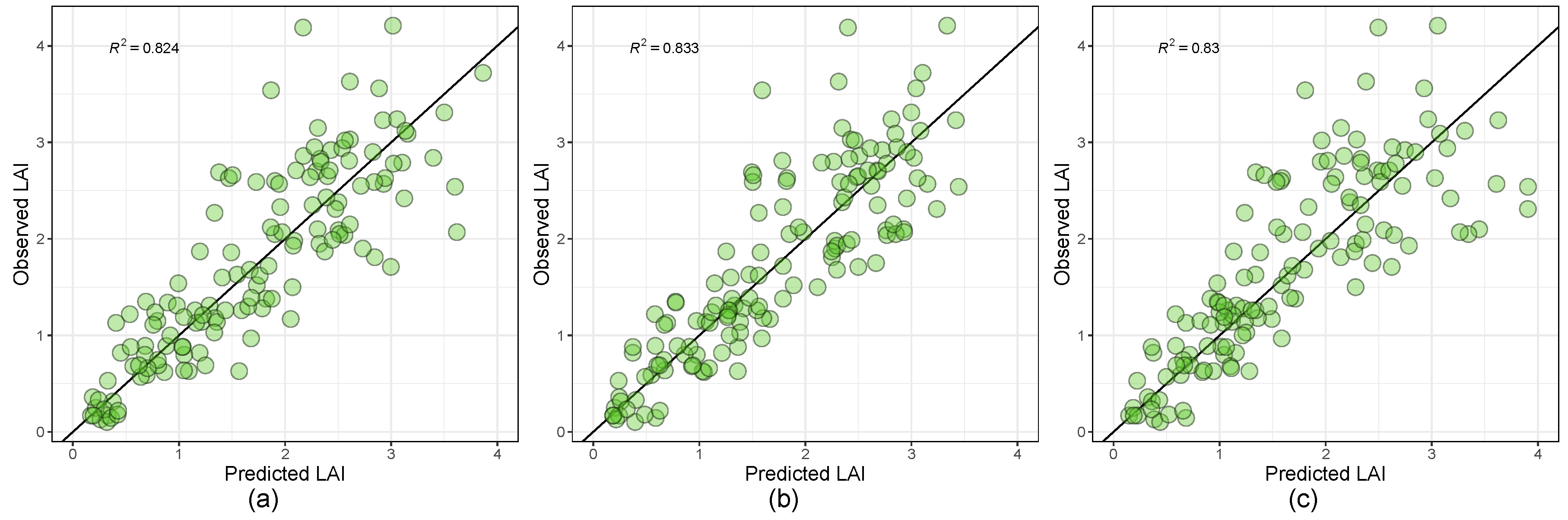
3.4. Leaf Area Index Estimation Based on Regression Modeling Strategies with Dimensionality Reduction
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| UAV | unmanned aerial vehicle |
| LAI | leaf area index |
| PAR | photosynthetically active radiation |
| GIS | geographical information systems |
| PA | precision agriculture |
| SNIG | National Geographic Information System |
| NIR | near infrared |
| DSM | digital surface model |
| DTM | digital terrain model |
| CHM | canopy height model |
| NDVI | Normalized Difference Vegetation Index |
| GNDVI | Green Normalized Difference Vegetation Index |
| GRVI | Green Red Vegetation Index |
| NDRE | Normalized Difference Red Edge |
| SAVI | Soil Adjusted Vegetation Index |
| RDVI | Renormalized Difference Vegetation Index |
| RVI | Ratio Vegetation Index |
| NDExNIR | Normalized Difference Excess Near Infrared |
| NDExRE | Normalized Difference Excess Red Edge |
| RMSE | root mean square error |
| MAE | mean absolute error |
| coefficient of determination | |
| r | Pearson correlation coefficient |
| rvmPoly | Relevance Vector Machines with Polynomial Kernel |
| SVM | Support Vector Machine |
| VARI | Visible Atmospherically Resistant Index |
| EVI | Enhanced Vegetation Index |
| EVI2 | Enhanced Vegetation Index 2 |
| MCARI2 | Modified Chlorophyll Absorption Ration Index 2 |
References
- Watson, D.J. Comparative physiological studies on the growth of field crops: I. Variation in net assimilation rate and leaf area between species and varieties, and within and between years. Ann. Bot. 1947, 11, 41–76. [Google Scholar] [CrossRef]
- Song, C. Optical remote sensing of forest leaf area index and biomass. Prog. Phys. Geogr. 2013, 37, 98–113. [Google Scholar] [CrossRef]
- Doughty, C.E.; Goulden, M.L. Seasonal patterns of tropical forest leaf area index and CO2 exchange. J. Geophys. Res. Biogeosci. 2008, 113. [Google Scholar] [CrossRef]
- Chason, J.W.; Baldocchi, D.D.; Huston, M.A. A comparison of direct and indirect methods for estimating forest canopy leaf area. Agric. For. Meteorol. 1991, 57, 107–128. [Google Scholar] [CrossRef]
- Nilson, T. A theoretical analysis of the frequency of gaps in plant stands. Agric. Meteorol. 1971, 8, 25–38. [Google Scholar] [CrossRef]
- Bréda, N.J. Ground-based measurements of leaf area index: A review of methods, instruments and current controversies. J. Exp. Bot. 2003, 54, 2403–2417. [Google Scholar] [CrossRef]
- Berni, J.; Zarco-Tejada, P.; Suarez, L.; González-Dugo, V.; Fereres, E. Remote sensing of vegetation from UAV platforms using lightweight multispectral and thermal imaging sensors. Int. Arch. Photogramm. Remote Sens. Spat. Inform. Sci. 2009, 38, 6. [Google Scholar]
- Sishodia, R.P.; Ray, R.L.; Singh, S.K. Applications of remote sensing in precision agriculture: A review. Remote Sens. 2020, 12, 3136. [Google Scholar] [CrossRef]
- Pádua, L.; Adão, T.; Hruška, J.; Sousa, J.J.; Peres, E.; Morais, R.; Sousa, A. Very high resolution aerial data to support multi-temporal precision agriculture information management. Procedia Comput. Sci. 2017, 121, 407–414. [Google Scholar] [CrossRef]
- White, W.A.; Alsina, M.M.; Nieto, H.; McKee, L.G.; Gao, F.; Kustas, W.P. Determining a robust indirect measurement of leaf area index in California vineyards for validating remote sensing-based retrievals. Irrig. Sci. 2019, 37, 269–280. [Google Scholar] [CrossRef]
- Mourad, R.; Jaafar, H.; Anderson, M.; Gao, F. Assessment of leaf area index models using harmonized landsat and sentinel-2 surface reflectance data over a semi-arid irrigated landscape. Remote Sens. 2020, 12, 3121. [Google Scholar] [CrossRef]
- Johnson, L.; Roczen, D.; Youkhana, S.; Nemani, R.; Bosch, D. Mapping vineyard leaf area with multispectral satellite imagery. Comput. Electron. Agric. 2003, 38, 33–44. [Google Scholar] [CrossRef]
- Kang, Y.; Özdoğan, M.; Zipper, S.C.; Román, M.O.; Walker, J.; Hong, S.Y.; Marshall, M.; Magliulo, V.; Moreno, J.; Alonso, L.; et al. How universal is the relationship between remotely sensed vegetation indices and crop leaf area index? A global assessment. Remote Sens. 2016, 8, 597. [Google Scholar] [CrossRef]
- González Piqueras, J. Evapotranspiración de la Cubierta Vegetal Mediante la Determinación del Coeficiente de Cultivo por Teledetección. Extensión a Escala Regional: Acuífero 08.29 Mancha Oriental; Facultat de Física, Universitat de València: Barcelona, Spain, 2006. [Google Scholar]
- Tian, J.; Wang, L.; Li, X.; Gong, H.; Shi, C.; Zhong, R.; Liu, X. Comparison of UAV and WorldView-2 imagery for mapping leaf area index of mangrove forest. Int. J. Appl. Earth Obs. Geoinf. 2017, 61, 22–31. [Google Scholar] [CrossRef]
- Myneni, R.B.; Ramakrishna, R.; Nemani, R.; Running, S.W. Estimation of global leaf area index and absorbed PAR using radiative transfer models. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1380–1393. [Google Scholar] [CrossRef]
- Pôças, I.; Paço, T.A.; Cunha, M.; Andrade, J.A.; Silvestre, J.; Sousa, A.; Santos, F.L.; Pereira, L.S.; Allen, R.G. Satellite-based evapotranspiration of a super-intensive olive orchard: Application of METRIC algorithms. Biosyst. Eng. 2014, 128, 69–81. [Google Scholar] [CrossRef]
- Pasqualotto, N.; Delegido, J.; Van Wittenberghe, S.; Rinaldi, M.; Moreno, J. Multi-crop green LAI estimation with a new simple Sentinel-2 LAI Index (SeLI). Sensors 2019, 19, 904. [Google Scholar] [CrossRef]
- Sun, L.; Gao, F.; Anderson, M.C.; Kustas, W.P.; Alsina, M.M.; Sanchez, L.; Sams, B.; McKee, L.; Dulaney, W.; White, W.A.; et al. Daily mapping of 30 m LAI and NDVI for grape yield prediction in California vineyards. Remote Sens. 2017, 9, 317. [Google Scholar] [CrossRef]
- Chen, Z.; Jia, K.; Xiao, C.; Wei, D.; Zhao, X.; Lan, J.; Wei, X.; Yao, Y.; Wang, B.; Sun, Y.; et al. Leaf area index estimation algorithm for GF-5 hyperspectral data based on different feature selection and machine learning methods. Remote Sens. 2020, 12, 2110. [Google Scholar] [CrossRef]
- Wang, T.; Xiao, Z.; Liu, Z. Performance evaluation of machine learning methods for leaf area index retrieval from time-series MODIS reflectance data. Sensors 2017, 17, 81. [Google Scholar] [CrossRef]
- Pajares, G. Overview and current status of remote sensing applications based on unmanned aerial vehicles (UAVs). Photogramm. Eng. Remote Sens. 2015, 81, 281–330. [Google Scholar] [CrossRef]
- Kalisperakis, I.; Stentoumis, C.; Grammatikopoulos, L.; Karantzalos, K. Leaf area index estimation in vineyards from UAV hyperspectral data, 2D image mosaics and 3D canopy surface models. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40, 299. [Google Scholar] [CrossRef]
- Vélez, S.; Poblete-Echeverría, C.; Rubio, J.A.; Vacas, R.; Barajas, E. Estimation of Leaf Area Index in vineyards by analysing projected shadows using UAV imagery. OENO One 2021, 55, 159–180. [Google Scholar] [CrossRef]
- Ilniyaz, O.; Kurban, A.; Du, Q. Leaf Area Index Estimation of Pergola-Trained Vineyards in Arid Regions Based on UAV RGB and Multispectral Data Using Machine Learning Methods. Remote Sens. 2022, 14, 415. [Google Scholar] [CrossRef]
- Wu, S.; Deng, L.; Guo, L.; Wu, Y. Wheat leaf area index prediction using data fusion based on high-resolution unmanned aerial vehicle imagery. Plant Methods 2022, 18, 1–16. [Google Scholar] [CrossRef]
- Caruso, G.; Zarco-Tejada, P.J.; González-Dugo, V.; Moriondo, M.; Tozzini, L.; Palai, G.; Rallo, G.; Hornero, A.; Primicerio, J.; Gucci, R. High-resolution imagery acquired from an unmanned platform to estimate biophysical and geometrical parameters of olive trees under different irrigation regimes. PLoS ONE 2019, 14, e0210804. [Google Scholar] [CrossRef]
- Yao, X.; Wang, N.; Liu, Y.; Cheng, T.; Tian, Y.; Chen, Q.; Zhu, Y. Estimation of wheat LAI at middle to high levels using unmanned aerial vehicle narrowband multispectral imagery. Remote Sens. 2017, 9, 1304. [Google Scholar] [CrossRef]
- Peng, X.; Han, W.; Ao, J.; Wang, Y. Assimilation of LAI derived from UAV multispectral data into the SAFY model to estimate maize yield. Remote Sens. 2021, 13, 1094. [Google Scholar] [CrossRef]
- Qiao, L.; Gao, D.; Zhao, R.; Tang, W.; An, L.; Li, M.; Sun, H. Improving estimation of LAI dynamic by fusion of morphological and vegetation indices based on UAV imagery. Comput. Electron. Agric. 2022, 192, 106603. [Google Scholar] [CrossRef]
- Li, S.; Yuan, F.; Ata-UI-Karim, S.T.; Zheng, H.; Cheng, T.; Liu, X.; Tian, Y.; Zhu, Y.; Cao, W.; Cao, Q. Combining color indices and textures of UAV-based digital imagery for rice LAI estimation. Remote Sens. 2019, 11, 1763. [Google Scholar] [CrossRef]
- Gong, Y.; Yang, K.; Lin, Z.; Fang, S.; Wu, X.; Zhu, R.; Peng, Y. Remote estimation of leaf area index (LAI) with unmanned aerial vehicle (UAV) imaging for different rice cultivars throughout the entire growing season. Plant Methods 2021, 17, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Martins, L.; Castro, J.P.; Gouveia, M.E. Biological control of chestnut blight in Portugal. In Proceedings of the II European Congress on Chestnut 1043, Debrecen, Hungary, 9–12 October 2013; pp. 51–56. [Google Scholar]
- Valverde, A.; González-Tirante, M.; Medina-Sierra, M.; Rivas, R.; Santa-Regina, I.; Igual, J.M. Culturable bacterial diversity from the chestnut (Castanea sativa Mill.) phyllosphere and antagonism against the fungi causing the chestnut blight and ink diseases. AIMS Microbiol. 2017, 3, 293. [Google Scholar] [CrossRef] [PubMed]
- Rigling, D.; Prospero, S. Cryphonectria parasitica, the causal agent of chestnut blight: Invasion history, population biology and disease control. Mol. Plant Pathol. 2018, 19, 7–20. [Google Scholar] [CrossRef] [PubMed]
- Portela, E.; Roboredo, M.; Louzada, J. Assessment and description of magnesium deficiencies in chestnut groves. J. Plant Nutr. 2003, 26, 503–523. [Google Scholar] [CrossRef]
- Aebi, A.; Schönrogge, K.; Melika, G.; Alma, A.; Bosio, G.; Quacchia, A.; Picciau, L.; Abe, Y.; Moriya, S.; Yara, K.; et al. Parasitoid recruitment to the globally invasive chestnut gall wasp Dryocosmus kuriphilus. In Galling Arthropods and Their Associates; Springer: Berlin/Heidelberg, Germany, 2006; pp. 103–121. [Google Scholar]
- Gehring, E.; Bellosi, B.; Quacchia, A.; Conedera, M. Assessing the impact of Dryocosmus kuriphilus on the chestnut tree: Branch architecture matters. J. Pest Sci. 2018, 91, 189–202. [Google Scholar] [CrossRef]
- Serdar, Ü.; Demirsoy, H. Non-destructive leaf area estimation in chestnut. Sci. Hortic. 2006, 108, 227–230. [Google Scholar] [CrossRef]
- Demirsoy, H. Leaf area estimation in some species of fruit tree by using models as a non-destructive method. Fruits 2009, 64, 45–51. [Google Scholar] [CrossRef]
- Tokár, F. Leaf area index (LAI), production and silvicultural practice in European chestnut (Castanea sativa Mill.) monocultures. Folia Oecologica 2004, 31, 111. [Google Scholar]
- Chianucci, F.; Macfarlane, C.; Pisek, J.; Cutini, A.; Casa, R. Estimation of foliage clumping from the LAI-2000 Plant Canopy Analyzer: Effect of view caps. Trees 2015, 29, 355–366. [Google Scholar] [CrossRef]
- Cutini, A. New management options in chestnut coppices: An evaluation on ecological bases. For. Ecol. Manag. 2001, 141, 165–174. [Google Scholar] [CrossRef]
- Tokár, F. Production of the aboveground dendromass of European chestnut (Castanea sativa Mill.) in relation to leaf area index and climatic conditions. Folia Oecologica 2005, 32, 116. [Google Scholar]
- Covone, F.; Gratani, L. Age-related physiological and structural traits of chestnut coppices at the Castelli Romani Park (Italy). Ann. For. Sci. 2006, 63, 239–247. [Google Scholar] [CrossRef][Green Version]
- Manetti, M.; Pelleri, F.; Becagli, C.; Conedera, M.; Schleppi, P.; Zingg, A. Growth dynamics and leaf area index in chestnut coppices subjected to a new silvicultural approach: Single-tree-oriented management. In Proceedings of the II European Congress on Chestnut 1043, Debrecen, Hungary, 9–12 October 2013; pp. 121–128. [Google Scholar]
- Gondard, H.; Romane, F.; Grandjanny, M.; Li, J.; Aronson, J. Plant species diversity changes in abandoned chestnut (Castanea sativa) groves in southern France. Biodivers. Conserv. 2001, 10, 189–207. [Google Scholar] [CrossRef]
- Martins, L.M.; Lufinha, M.I.; Marques, C.P.; Abreu, C.G. Small format aerial photography to assess chestnut ink disease. For. Snow Landsc. Res 2001, 73, 357–360. [Google Scholar]
- Vannini, A.; Vettraino, A.; Fabi, A.; Montaghi, A.; Valentini, R.; Belli, C. Monitoring ink disease of chestnut with the airborne multispectral system ASPIS. In Proceedings of the III International Chestnut Congress 693, Chaves, Portugal, 20–23 October 2004; pp. 529–534. [Google Scholar]
- Ambrosini, I.; Gherardi, L.; Viti, M.L.; Maresi, G.; Turchetti, T. Monitoring diseases of chestnut stands by small format aerial photography. Geocarto Int. 1997, 12, 41–46. [Google Scholar] [CrossRef]
- Martins, L.; Castro, J.; Macedo, W.; Marques, C.; Abreu, C. Assessment of the spread of chestnut ink disease using remote sensing and geostatistical methods. Eur. J. Plant Pathol. 2007, 119, 159–164. [Google Scholar] [CrossRef]
- Castro, J.; Azevedo, J.; Martins, L. Temporal analysis of sweet chestnut decline in northeastern Portugal using geostatistical tools. In Proceedings of the I European Congress on Chestnut-Castanea 2009 866, Cuneo-Torino, Italy, 13–16 October 2009; pp. 405–410. [Google Scholar]
- Martins, L.; Castro, J.P.; Macedo, F.; Marques, C.; Abreu, C.G. Índices espectrais em fotografia aérea de infravermelho próximo na monitorização da doença tinta do castanheiro. In Proceedings of the 5º Congresso Florestal Nacional. SPCF-Sociedade Portuguesa de Ciências Florestais, Instituto Politécnico de Viseu, Viseu, Portugal, 16 May 2005. [Google Scholar]
- Montagnoli, A.; Fusco, S.; Terzaghi, M.; Kirschbaum, A.; Pflugmacher, D.; Cohen, W.B.; Scippa, G.S.; Chiatante, D. Estimating forest aboveground biomass by low density lidar data in mixed broad-leaved forests in the Italian Pre-Alps. For. Ecosyst. 2015, 2, 1–9. [Google Scholar] [CrossRef]
- Prada, M.; Cabo, C.; Hernández-Clemente, R.; Hornero, A.; Majada, J.; Martínez-Alonso, C. Assessing Canopy Responses to Thinnings for Sweet Chestnut Coppice with Time-Series Vegetation Indices Derived from Landsat-8 and Sentinel-2 Imagery. Remote Sens. 2020, 12, 3068. [Google Scholar] [CrossRef]
- Marchetti, F.; Waske, B.; Arbelo, M.; Moreno-Ruíz, J.A.; Alonso-Benito, A. Mapping Chestnut stands using bi-temporal VHR data. Remote Sens. 2019, 11, 2560. [Google Scholar] [CrossRef]
- Martins, L.; Castro, J.; Bento, R.; Sousa, J. Chestnut health monitoring by aerial photographs obtained by unnamed aerial vehicle. Rev. De Ciências Agrárias 2015, 38, 184–190. [Google Scholar]
- Pádua, L.; Hruška, J.; Bessa, J.; Adão, T.; Martins, L.M.; Gonçalves, J.A.; Peres, E.; Sousa, A.M.; Castro, J.P.; Sousa, J.J. Multi-temporal analysis of forestry and coastal environments using UASs. Remote Sens. 2017, 10, 24. [Google Scholar] [CrossRef]
- Marques, P.; Pádua, L.; Adão, T.; Hruška, J.; Peres, E.; Sousa, A.; Sousa, J.J. UAV-based automatic detection and monitoring of chestnut trees. Remote Sens. 2019, 11, 855. [Google Scholar] [CrossRef]
- Pádua, L.; Marques, P.; Adão, T.; Hruška, J.; Peres, E.; Morais, R.; Sousa, A.; Sousa, J.J. UAS-based imagery and photogrammetric processing for tree height and crown diameter extraction. In Proceedings of theInternational Conference on Geoinformatics and Data Analysis, Prague, Czech Republic, 20–22 April 2018; pp. 87–91. [Google Scholar]
- Pádua, L.; Marques, P.; Martins, L.; Sousa, A.; Peres, E.; Sousa, J.J. Monitoring of chestnut trees using machine learning techniques applied to UAV-based multispectral data. Remote Sens. 2020, 12, 3032. [Google Scholar] [CrossRef]
- Fernandez-Manso, A.; Cifuentes, J.; Sanz-Ablanero, E.; Quintano, C. Forest damage monitoring in South-Western Europe based on data from Unmanned Aerial Vehicles (UAV). In Proceedings of the Applications of Digital Image Processing XLIV, San Diego, CA, USA, 1–5 August 2021; Volume 11842, pp. 631–637. [Google Scholar]
- Candiago, S.; Remondino, F.; De Giglio, M.; Dubbini, M.; Gattelli, M. Evaluating multispectral images and vegetation indices for precision farming applications from UAV images. Remote Sens. 2015, 7, 4026–4047. [Google Scholar] [CrossRef]
- Instituto Nacional de Estatística, I. P. Estatísticas Agrícolas 2018; Instituto Nacional de Estatística, I.P.: Lisbon, Portugal, 2019.
- Albetis, J.; Duthoit, S.; Guttler, F.; Jacquin, A.; Goulard, M.; Poilvé, H.; Féret, J.B.; Dedieu, G. Detection of Flavescence dorée grapevine disease using unmanned aerial vehicle (UAV) multispectral imagery. Remote Sens. 2017, 9, 308. [Google Scholar] [CrossRef]
- Rouse, J.W., Jr.; Haas, R.H.; Schell, J.; Deering, D. Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation; Contractor Report; Texas A & M University, Remote Sensing Center: College Station, TX, USA, 1973. [Google Scholar]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Barnes, E.; Clarke, T.; Richards, S.; Colaizzi, P.; Haberland, J.; Kostrzewski, M.; Waller, P.; Choi, C.; Riley, E.; Thompson, T.; et al. Coincident detection of crop water stress, nitrogen status and canopy density using ground based multispectral data. In Proceedings of the Fifth International Conference on Precision Agriculture, Bloomington, MN, USA, 16–19 July 2000; Volume 1619, p. 6. [Google Scholar]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Roujean, J.L.; Breon, F.M. Estimating PAR absorbed by vegetation from bidirectional reflectance measurements. Remote Sens. Environ. 1995, 51, 375–384. [Google Scholar] [CrossRef]
- Richardson, A.J.; Wiegand, C. Distinguishing vegetation from soil background information. Photogramm. Eng. Remote Sens. 1977, 43, 1541–1552. [Google Scholar]
- Bradley, D.; Roth, G. Adaptive thresholding using the integral image. J. Graph. Tools 2007, 12, 13–21. [Google Scholar] [CrossRef]
- Maurer, C.R.; Qi, R.; Raghavan, V. A linear time algorithm for computing exact Euclidean distance transforms of binary images in arbitrary dimensions. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 265–270. [Google Scholar] [CrossRef]
- Meyer, F. Topographic distance and watershed lines. Signal Process. 1994, 38, 113–125. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Kuhn, M. Caret: Classification and Regression Training; R Package Version 6.0-93; 2022; Available online: https://cran.r-project.org/package=caret (accessed on 25 November 2022).
- Hamner, B.; Frasco, M. Metrics: Evaluation Metrics for Machine Learning; R Package Version 0.1.4; 2018; Available online: https://cran.r-project.org/package=Metrics (accessed on 25 November 2022).
- Tipping, M. The Relevance Vector Machine. In Proceedings of the Advances in Neural Information Processing Systems; Solla, S., Leen, T., Müller, K., Eds.; MIT Press: Cambridge, MA, USA, 1999; Volume 12. [Google Scholar]
- Burden, F.; Winkler, D. Bayesian Regularization of Neural Networks. In Artificial Neural Networks: Methods and Applications; Livingstone, D.J., Ed.; Humana Press: Totowa, NJ, USA, 2009; pp. 23–42. [Google Scholar] [CrossRef]
- Ishwaran, H.; Rao, J.S. Spike and slab variable selection: Frequentist and Bayesian strategies. Ann. Stat. 2005, 33, 730–773. [Google Scholar] [CrossRef]
- Pádua, L.; Marques, P.; Martins, L.; Sousa, A.; Peres, E.; Sousa, J.J. Estimation of Leaf Area Index in Chestnut Trees using Multispectral Data from an Unmanned Aerial Vehicle. In Proceedings of the IGARSS 2020–2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2000; IEEE: Piscataway Township, NJ, USA, 2020; pp. 6503–6506. [Google Scholar]
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel algorithms for remote estimation of vegetation fraction. Remote Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.R.; Didan, K.; Miura, T. Development of a two-band enhanced vegetation index without a blue band. Remote Sens. Environ. 2008, 112, 3833–3845. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Liang, L.; Di, L.; Zhang, L.; Deng, M.; Qin, Z.; Zhao, S.; Lin, H. Estimation of crop LAI using hyperspectral vegetation indices and a hybrid inversion method. Remote Sens. Environ. 2015, 165, 123–134. [Google Scholar] [CrossRef]
- Tian, M.; Ban, S.; Chang, Q.; You, M.; Luo, D.; Wang, L.; Wang, S. Use of hyperspectral images from UAV-based imaging spectroradiometer to estimate cotton leaf area index. Trans. Chin. Soc. Agric. Eng. 2016, 32, 102–108. [Google Scholar]



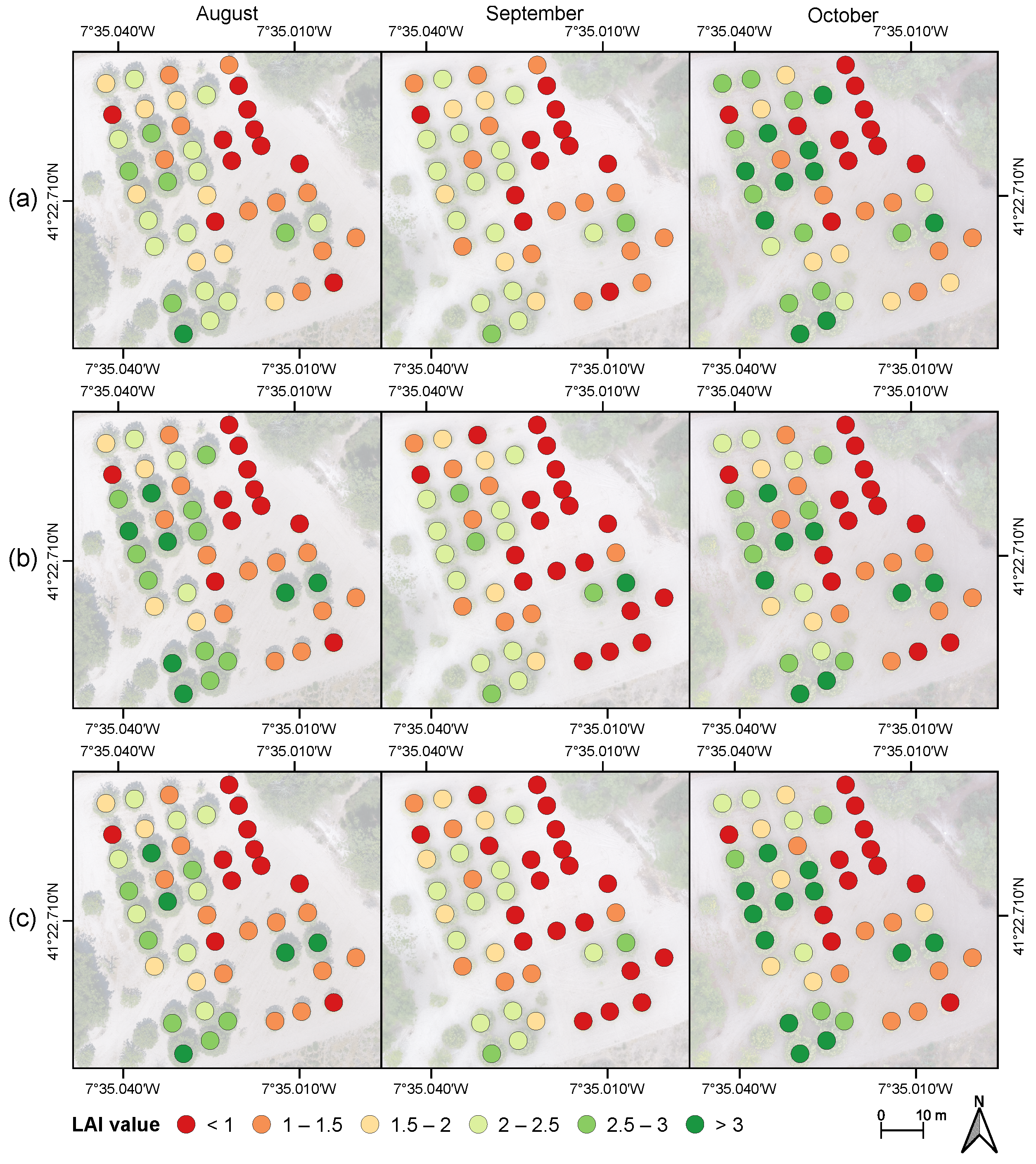
| Period | Mean | SD | CV | q0.25 | q0.75 | Min | Max |
|---|---|---|---|---|---|---|---|
| August | 1.581 | 0.909 | 0.575 | 0.156 | 3.214 | 0.103 | 3.630 |
| September | 1.657 | 0.951 | 0.574 | 0.170 | 3.125 | 0.170 | 3.540 |
| October | 2.018 | 1.061 | 0.526 | 0.185 | 4.131 | 0.130 | 4.210 |
| Covariate | August | September | October | All Values |
|---|---|---|---|---|
| GNDVI | 0.858 | 0.896 | 0.889 | 0.842 |
| NDExRE | 0.852 | 0.877 | 0.868 | 0.822 |
| NDVI | 0.856 | 0.875 | 0.863 | 0.820 |
| Crown area | 0.816 | 0.834 | 0.788 | 0.803 |
| Height | 0.819 | 0.769 | 0.773 | 0.784 |
| RVI | 0.862 | 0.870 | 0.825 | 0.780 |
| NDExNIR | 0.869 | 0.895 | 0.876 | 0.758 |
| Crown diameter | 0.795 | 0.778 | 0.710 | 0.754 |
| RDVI | 0.870 | 0.852 | 0.879 | 0.703 |
| GRVI | 0.799 | 0.831 | 0.805 | 0.700 |
| SAVI | 0.867 | 0.824 | 0.878 | 0.562 |
| NDRE | 0.837 | 0.876 | 0.837 | 0.364 |
| Regression Model Type | RMSE | MAE | sd | RMSEsd | MAEsd | |
|---|---|---|---|---|---|---|
| Relevance Vector Machines with Polynomial Kernel | 0.833 | 0.343 | 0.273 | 0.098 | 0.082 | 0.076 |
| Bayesian Regularized Neural Networks | 0.830 | 0.348 | 0.267 | 0.093 | 0.080 | 0.065 |
| Linear model with leap backward | 0.824 | 0.367 | 0.285 | 0.097 | 0.109 | 0.088 |
| Spike and Slab Regression | 0.823 | 0.373 | 0.285 | 0.090 | 0.088 | 0.074 |
| Cubist | 0.818 | 0.366 | 0.281 | 0.112 | 0.083 | 0.059 |
| Projection Pursuit Regression | 0.815 | 0.354 | 0.276 | 0.110 | 0.083 | 0.059 |
| Boosted Regression Tree | 0.815 | 0.341 | 0.270 | 0.107 | 0.072 | 0.056 |
| Ridge Regression | 0.814 | 0.371 | 0.291 | 0.130 | 0.122 | 0.096 |
| The Bayesian Regression Lasso | 0.812 | 0.373 | 0.290 | 0.100 | 0.093 | 0.062 |
| Elastic net | 0.811 | 0.364 | 0.286 | 0.118 | 0.118 | 0.091 |
| Lm with Forward | 0.810 | 0.367 | 0.285 | 0.111 | 0.115 | 0.095 |
| Bayesian Ridge Regression | 0.809 | 0.369 | 0.284 | 0.110 | 0.087 | 0.064 |
| Boosted Generalized Linear Model | 0.807 | 0.370 | 0.286 | 0.106 | 0.102 | 0.082 |
| The Lasso Regression | 0.806 | 0.379 | 0.292 | 0.131 | 0.104 | 0.075 |
| Bayesian Ridge Regression (Model Averaged) | 0.805 | 0.372 | 0.288 | 0.128 | 0.096 | 0.077 |
| Bayesian Generalized Linear Model | 0.805 | 0.375 | 0.292 | 0.094 | 0.103 | 0.079 |
| Linear Regression with Stepwise Selection | 0.805 | 0.371 | 0.285 | 0.116 | 0.090 | 0.070 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pádua, L.; Chiroque-Solano, P.M.; Marques, P.; Sousa, J.J.; Peres, E. Mapping the Leaf Area Index of Castanea sativa Miller Using UAV-Based Multispectral and Geometrical Data. Drones 2022, 6, 422. https://doi.org/10.3390/drones6120422
Pádua L, Chiroque-Solano PM, Marques P, Sousa JJ, Peres E. Mapping the Leaf Area Index of Castanea sativa Miller Using UAV-Based Multispectral and Geometrical Data. Drones. 2022; 6(12):422. https://doi.org/10.3390/drones6120422
Chicago/Turabian StylePádua, Luís, Pamela M. Chiroque-Solano, Pedro Marques, Joaquim J. Sousa, and Emanuel Peres. 2022. "Mapping the Leaf Area Index of Castanea sativa Miller Using UAV-Based Multispectral and Geometrical Data" Drones 6, no. 12: 422. https://doi.org/10.3390/drones6120422
APA StylePádua, L., Chiroque-Solano, P. M., Marques, P., Sousa, J. J., & Peres, E. (2022). Mapping the Leaf Area Index of Castanea sativa Miller Using UAV-Based Multispectral and Geometrical Data. Drones, 6(12), 422. https://doi.org/10.3390/drones6120422








