Benchmarking Tracking Autopilots for Quadrotor Aerial Robotic System Using Heuristic Nonlinear Controllers
Abstract
1. Introduction
1.1. Motivation and Literature Review
1.2. Key Contributions
- A nested loop controller is proposed and implemented through three different control strategies: PD controller, nonlinear sliding-mode controller, nonlinear backstepping controller;
- Heuristic optimization tuning algorithms for the proposed control strategies are applied and investigated;
- A comprehensive benchmark is established for the developed approaches over a nonlinear dynamical quadrotor model.
1.3. Outline
2. Preliminaries and Notation
2.1. Notation
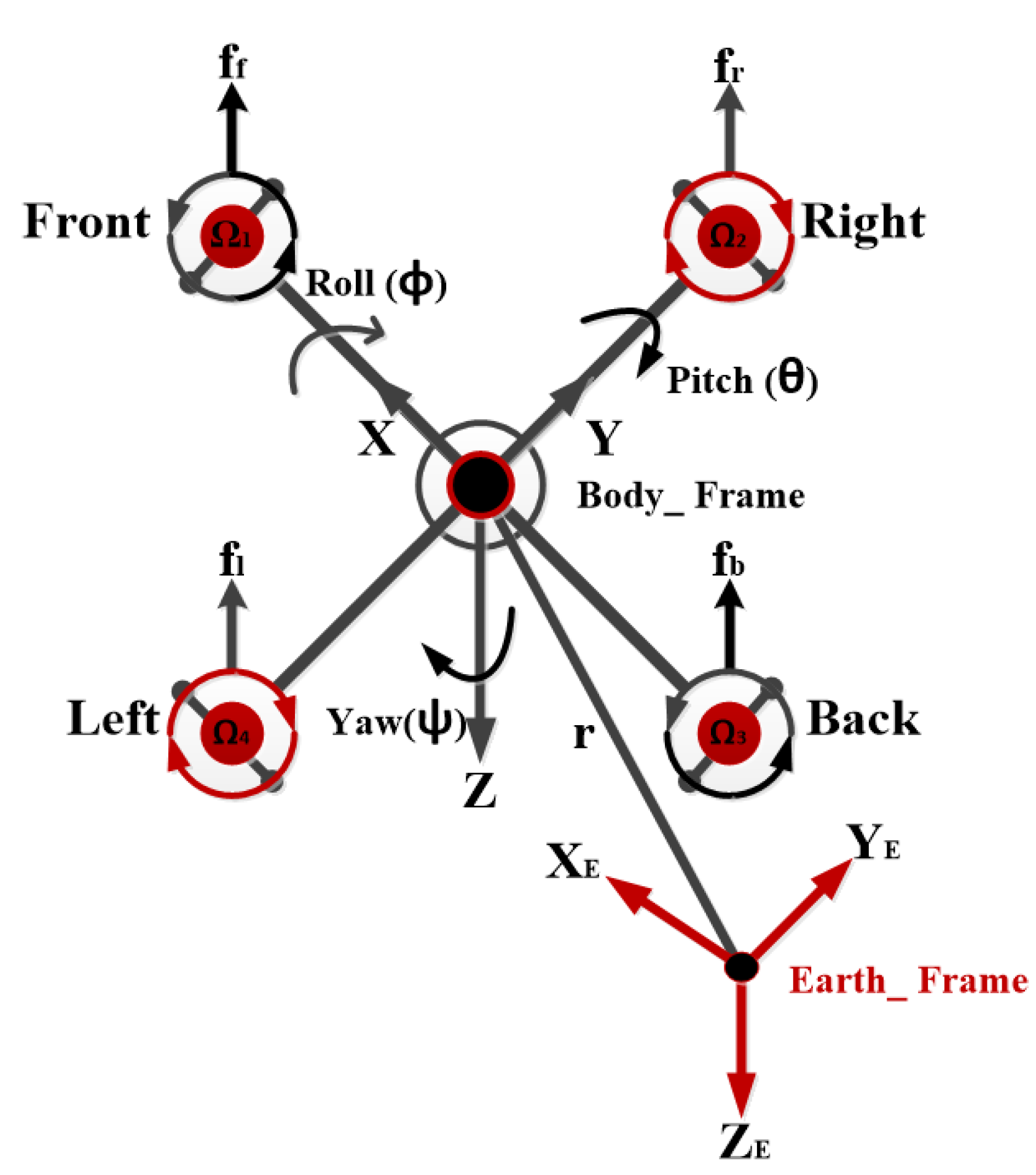
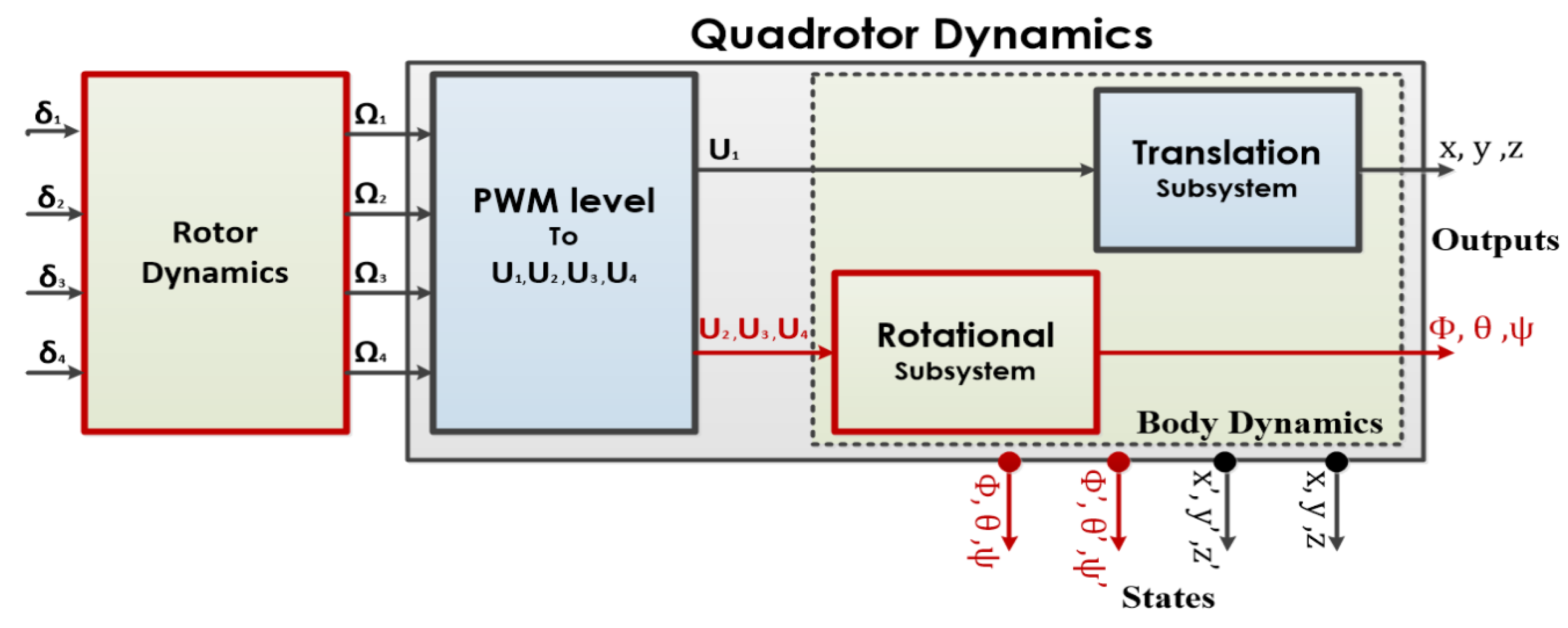
2.2. System Model
2.2.1. Kinematics Model
2.2.2. Dynamic Model
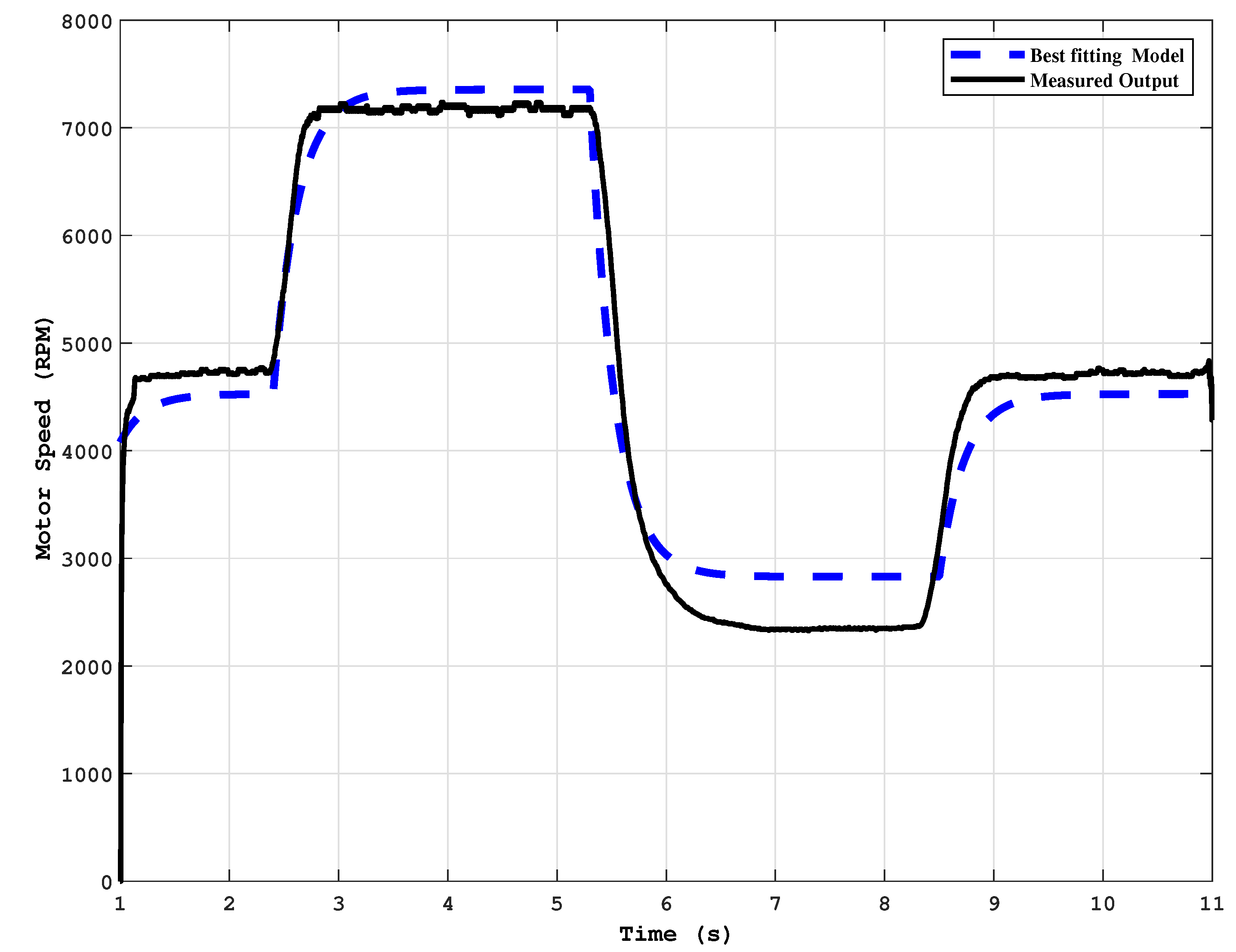
2.2.3. Actuation Model
2.2.4. State Space Model
3. Control Design
3.1. Inner Loop
3.1.1. PD Controller
3.1.2. Sliding Mode Control
3.1.3. Backstepping Controller
3.2. Outer Loop
4. Optimization Problem
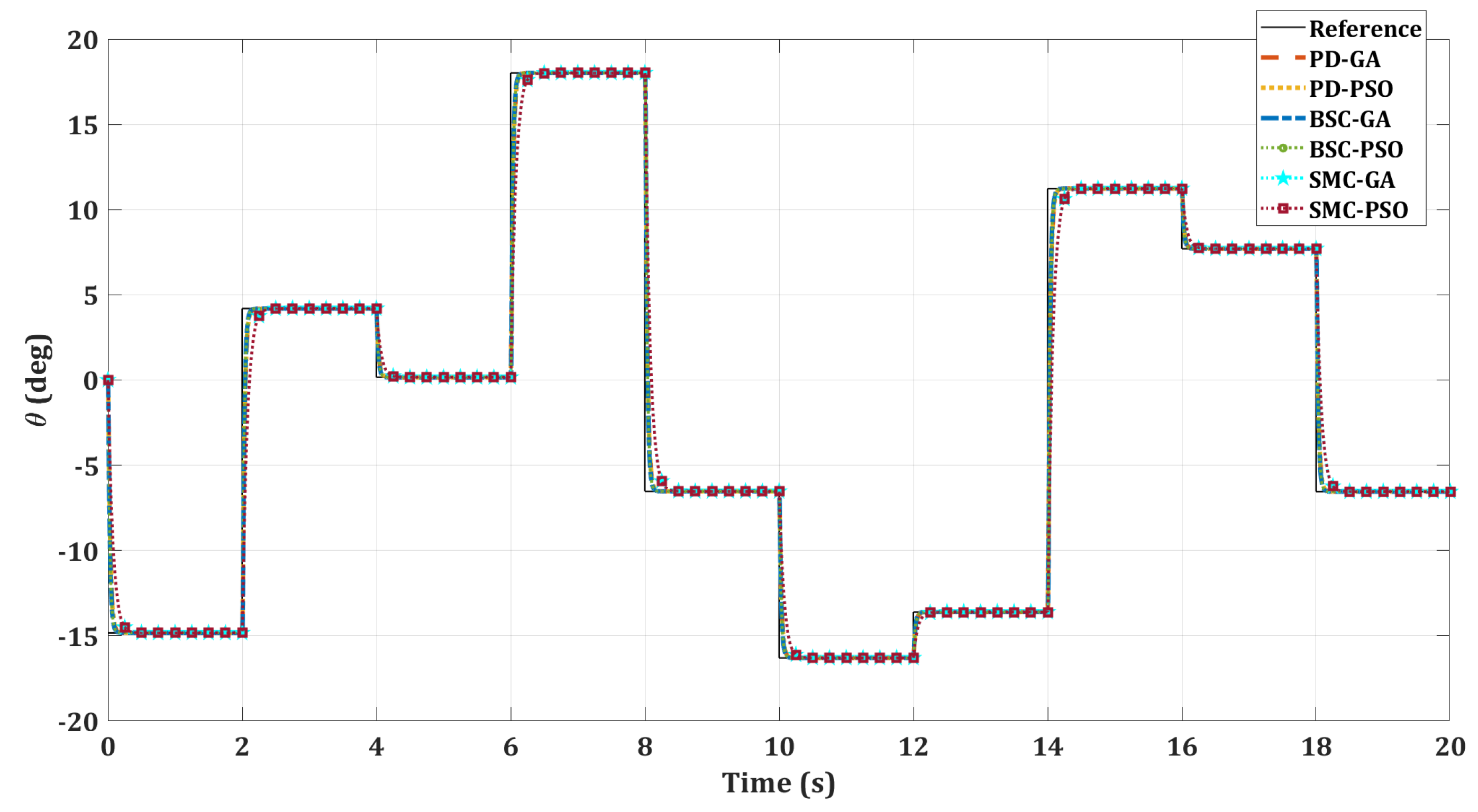
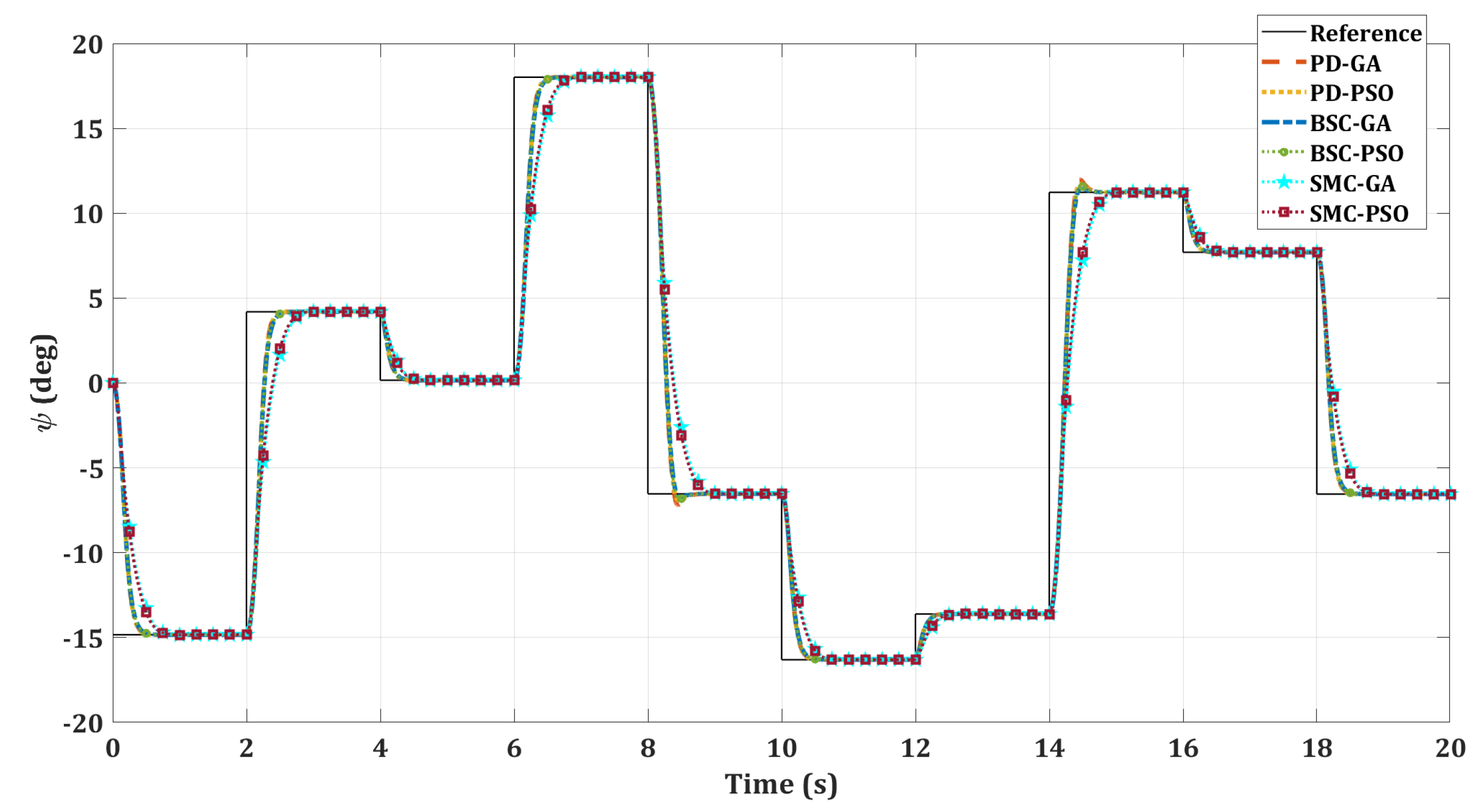
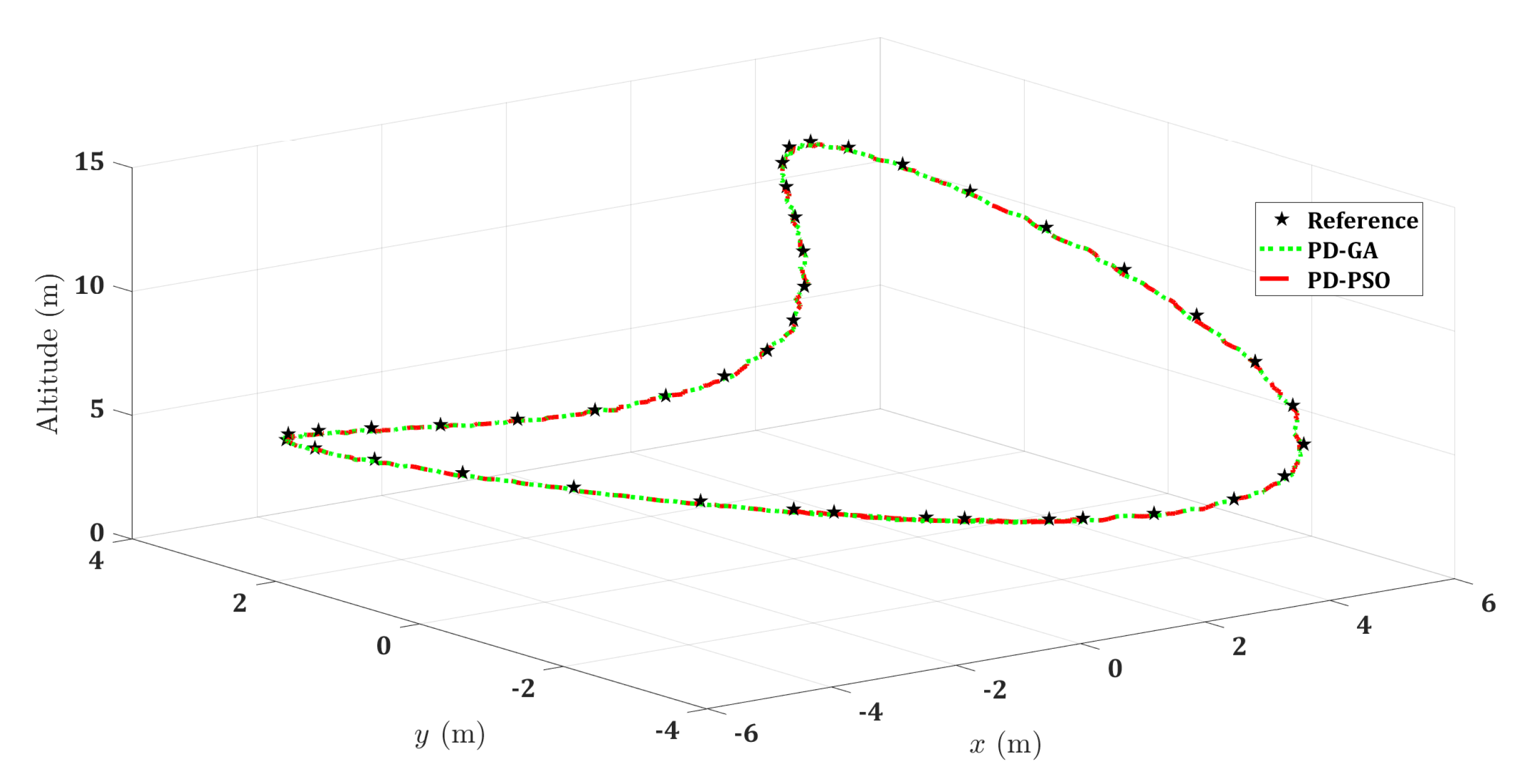
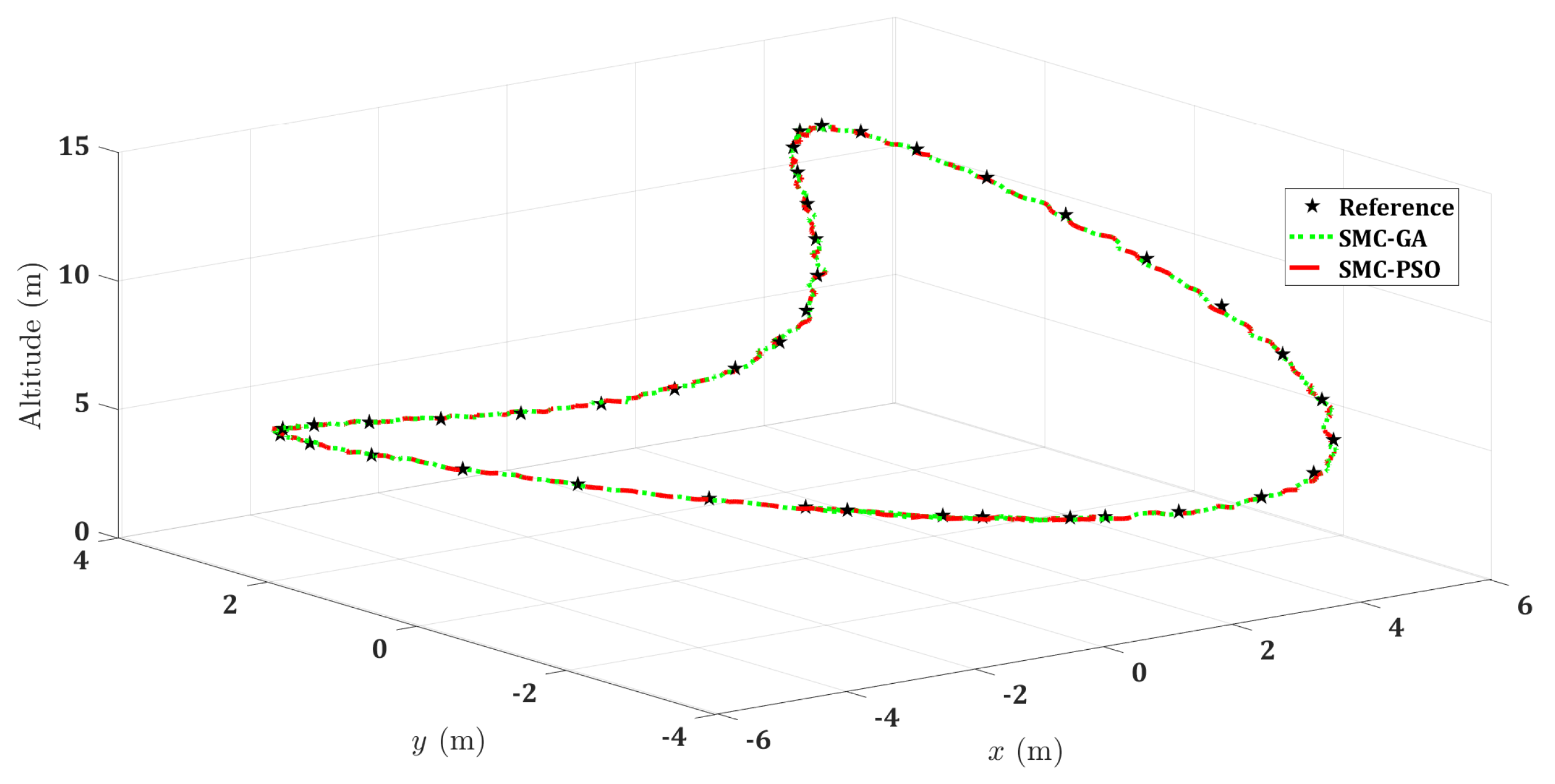
5. Results and Discussion
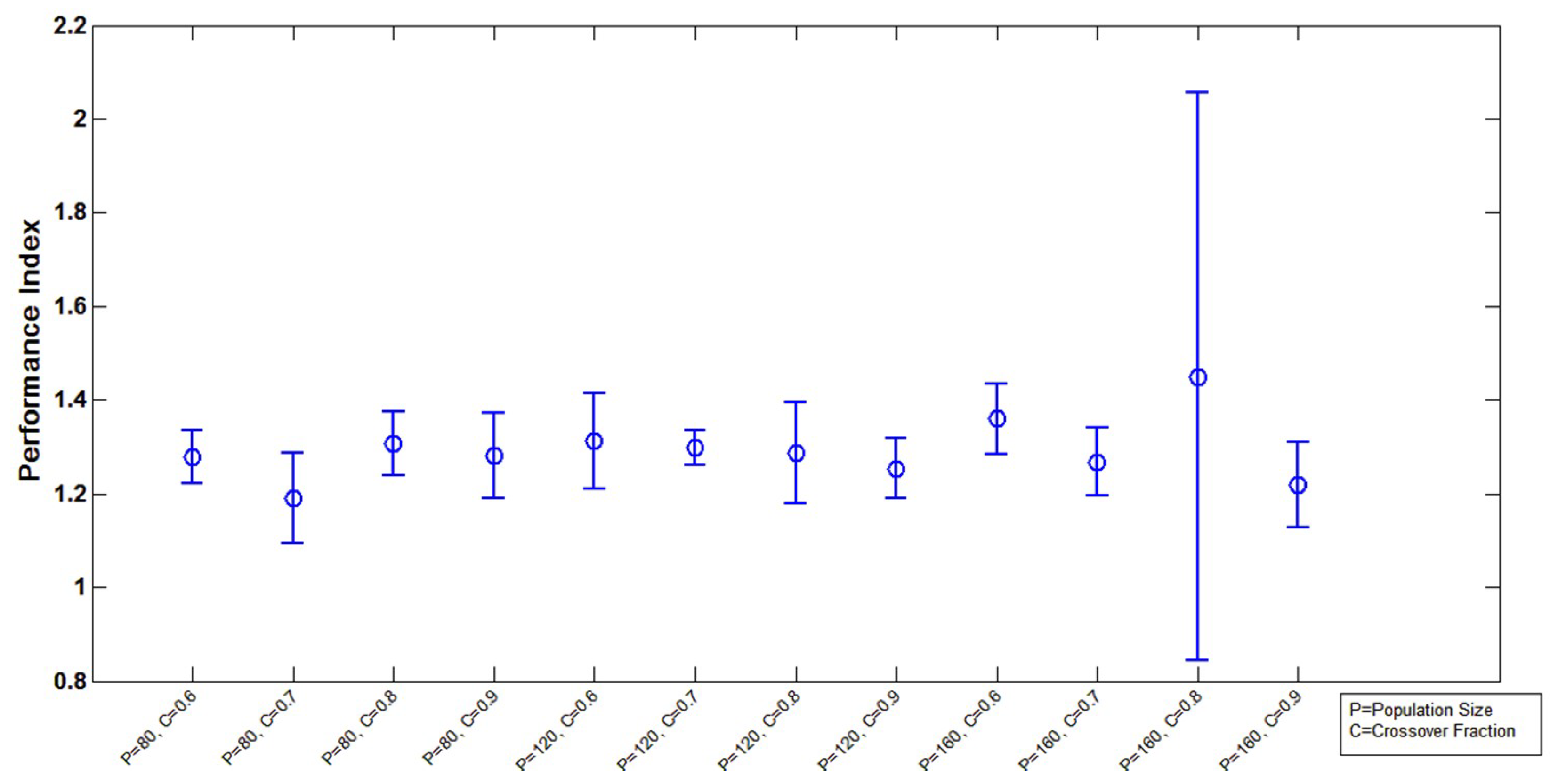
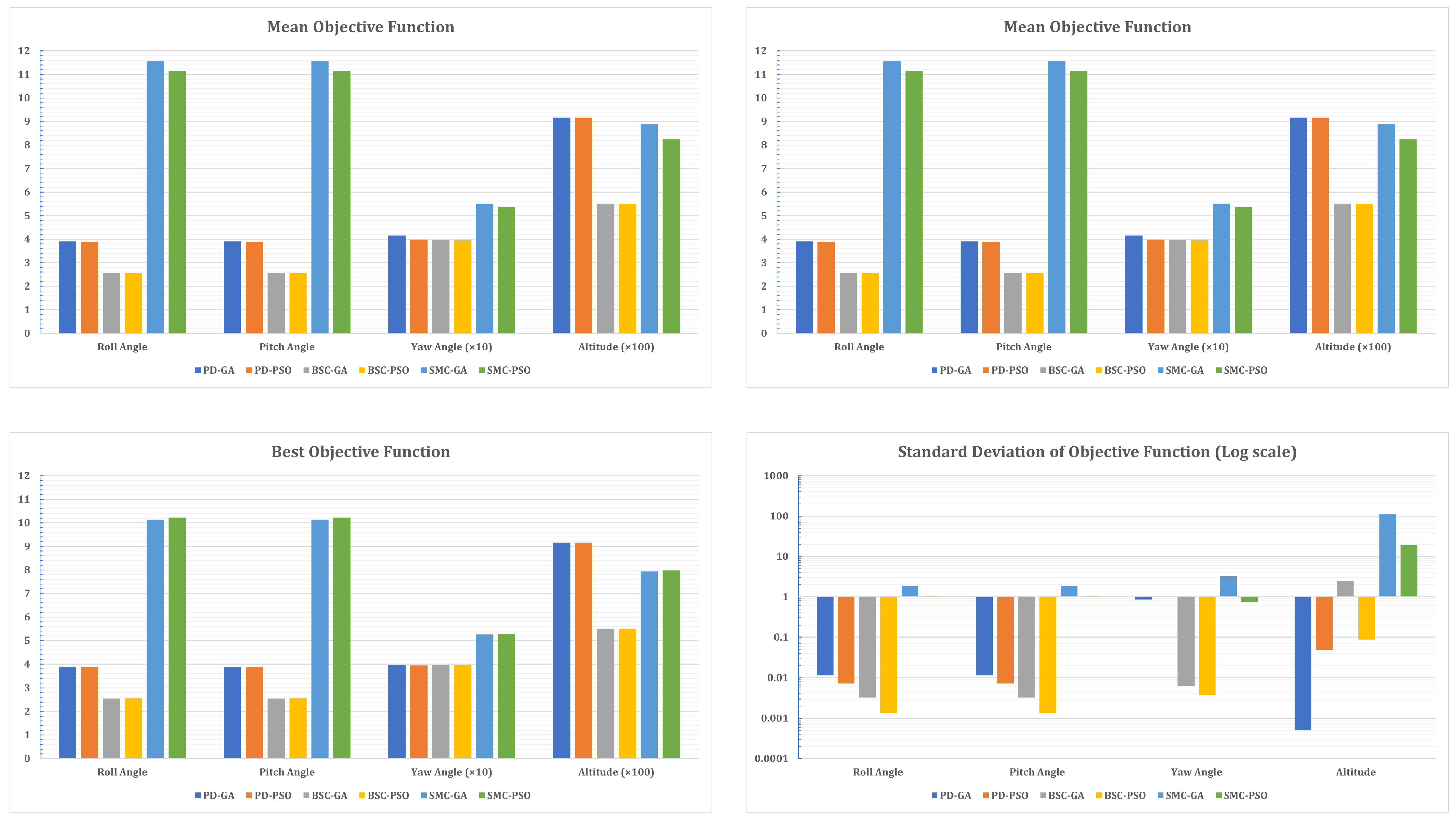
5.1. Optimization Algorithms Performance Analysis
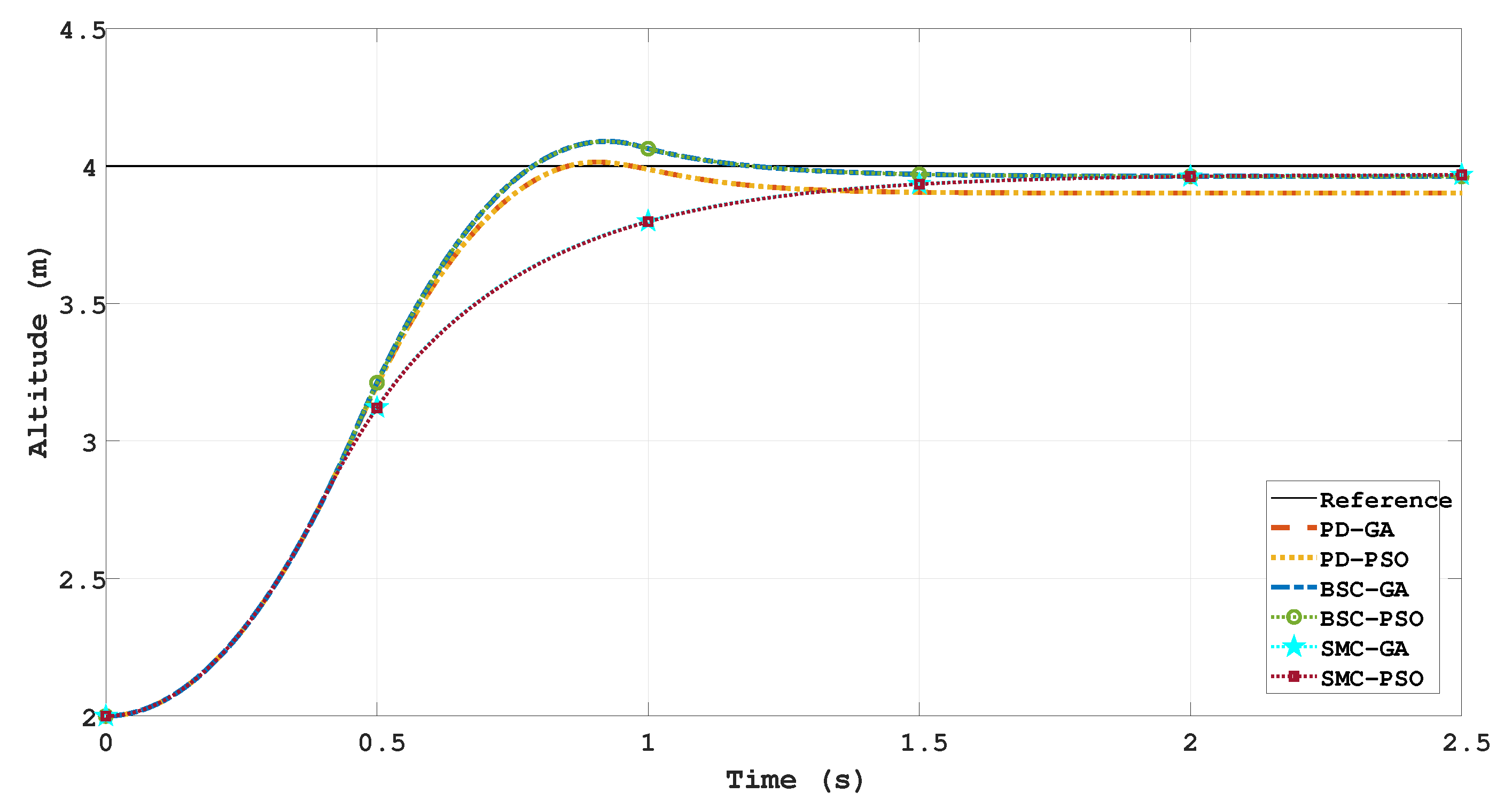
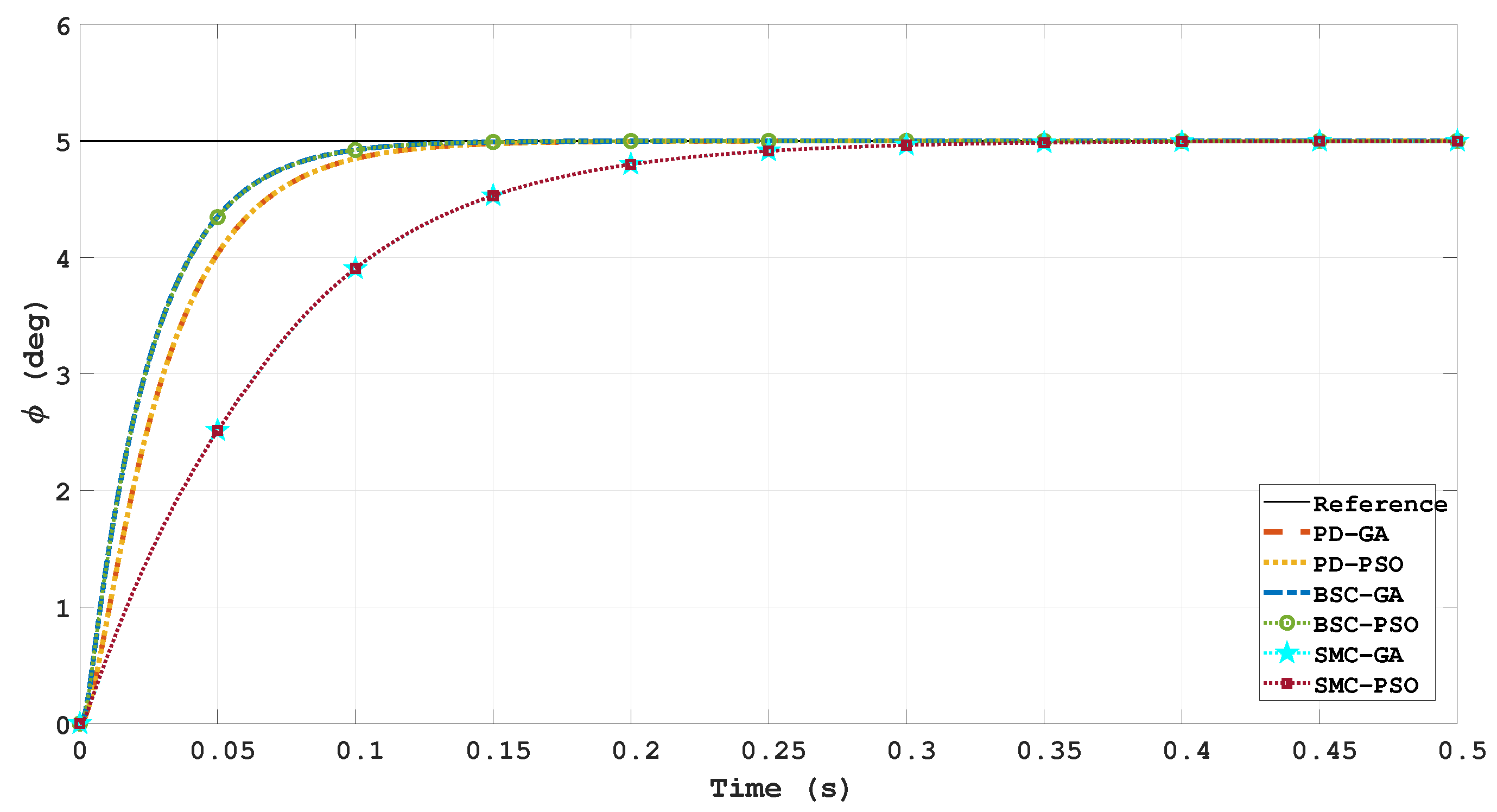
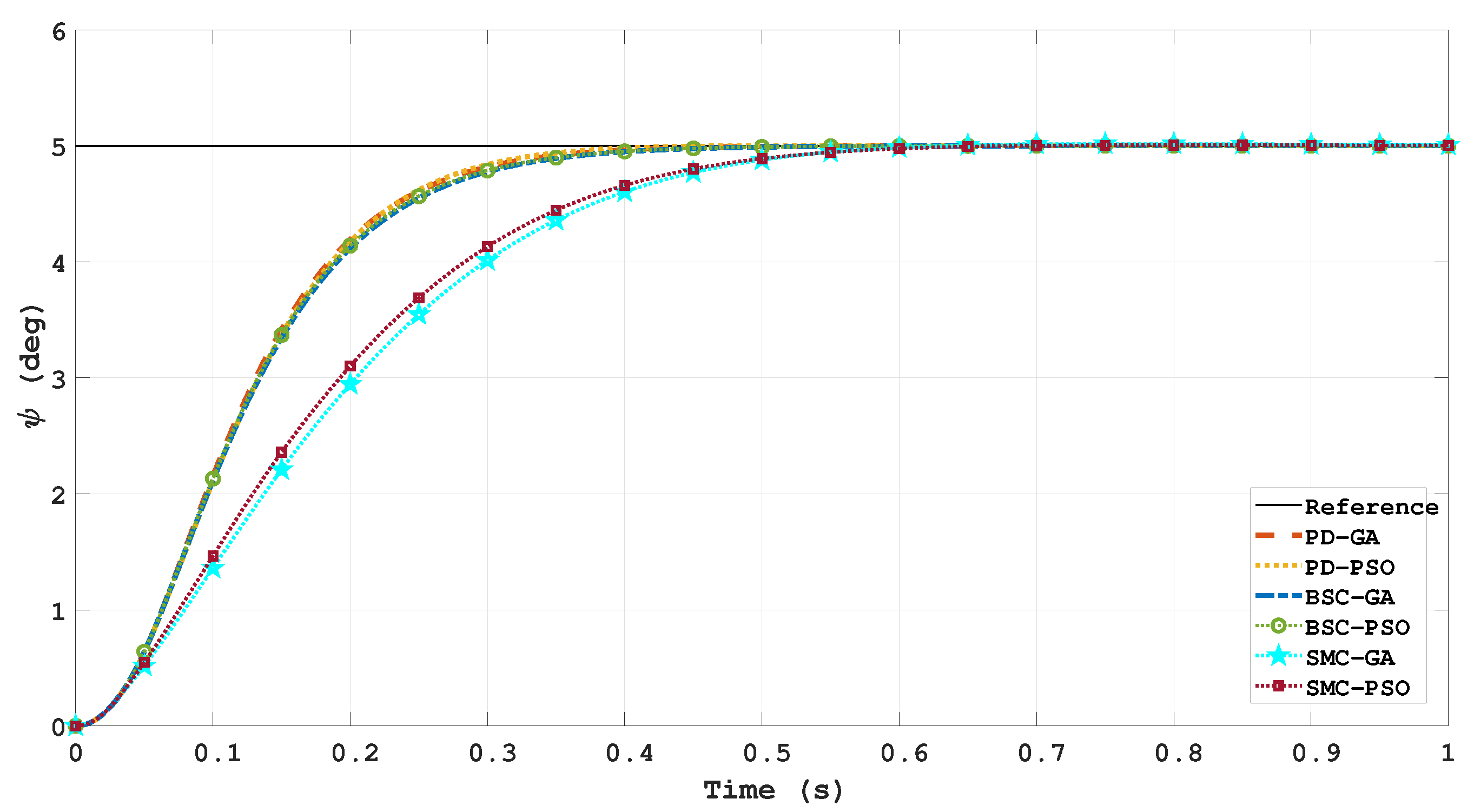
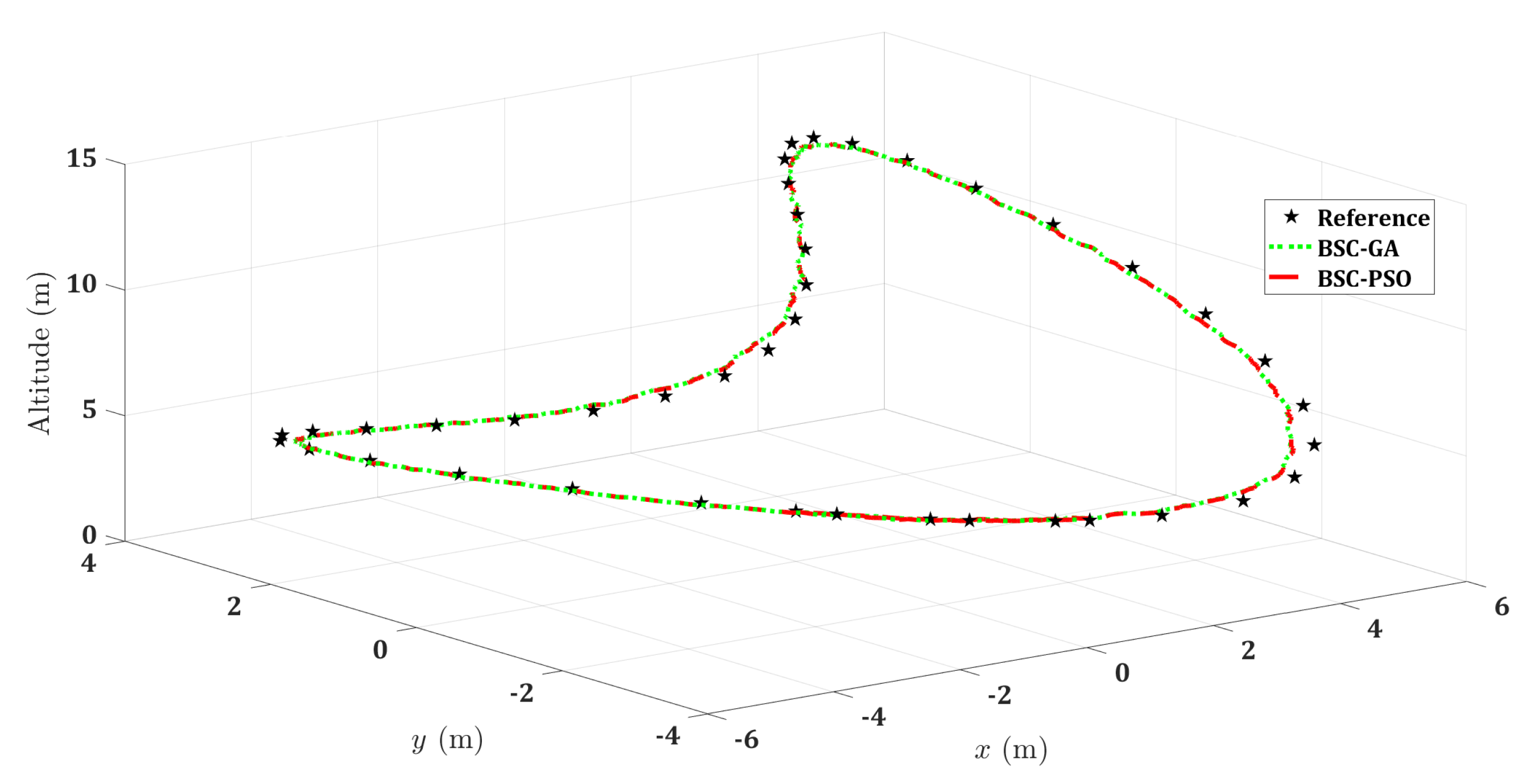
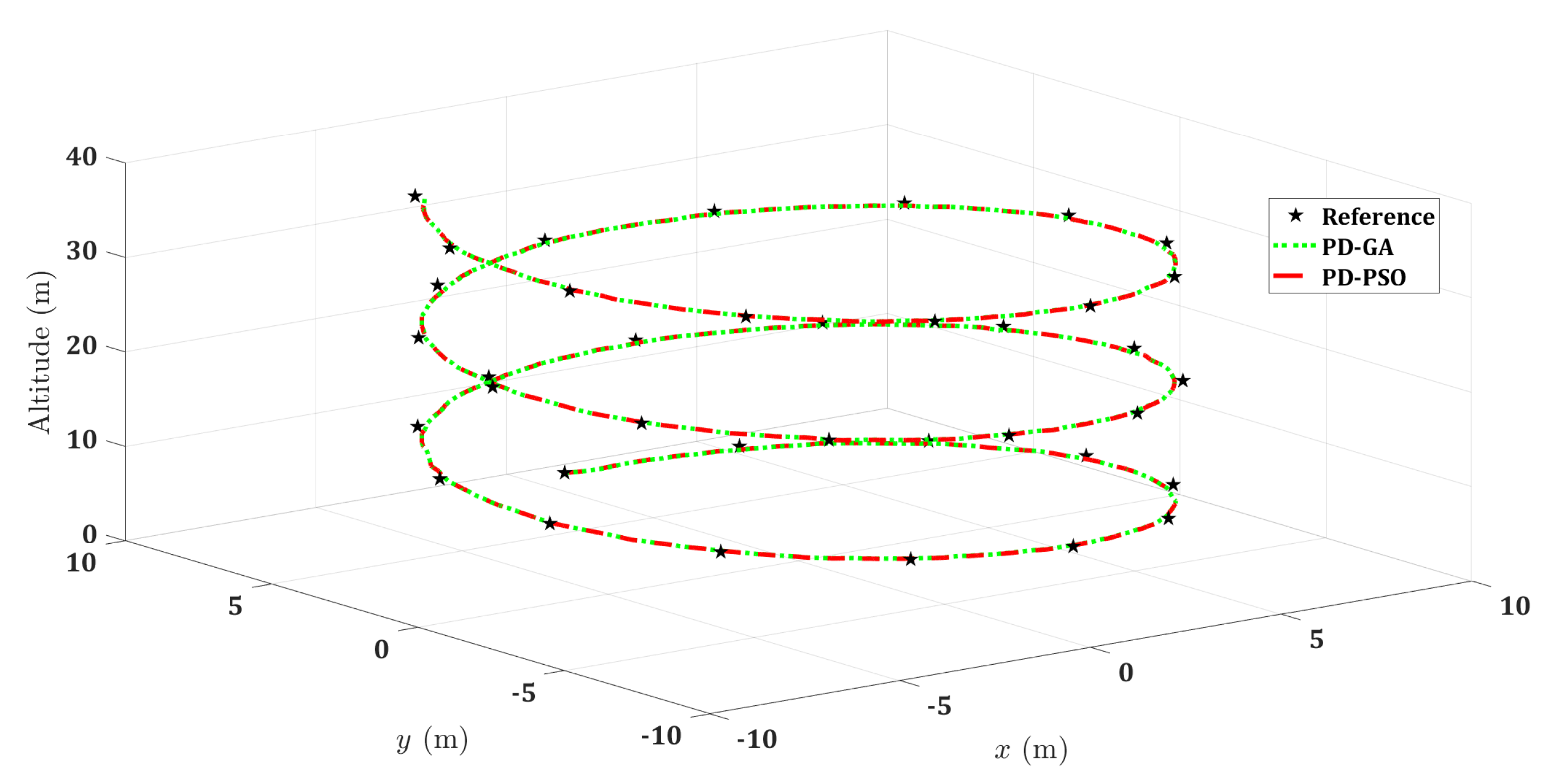
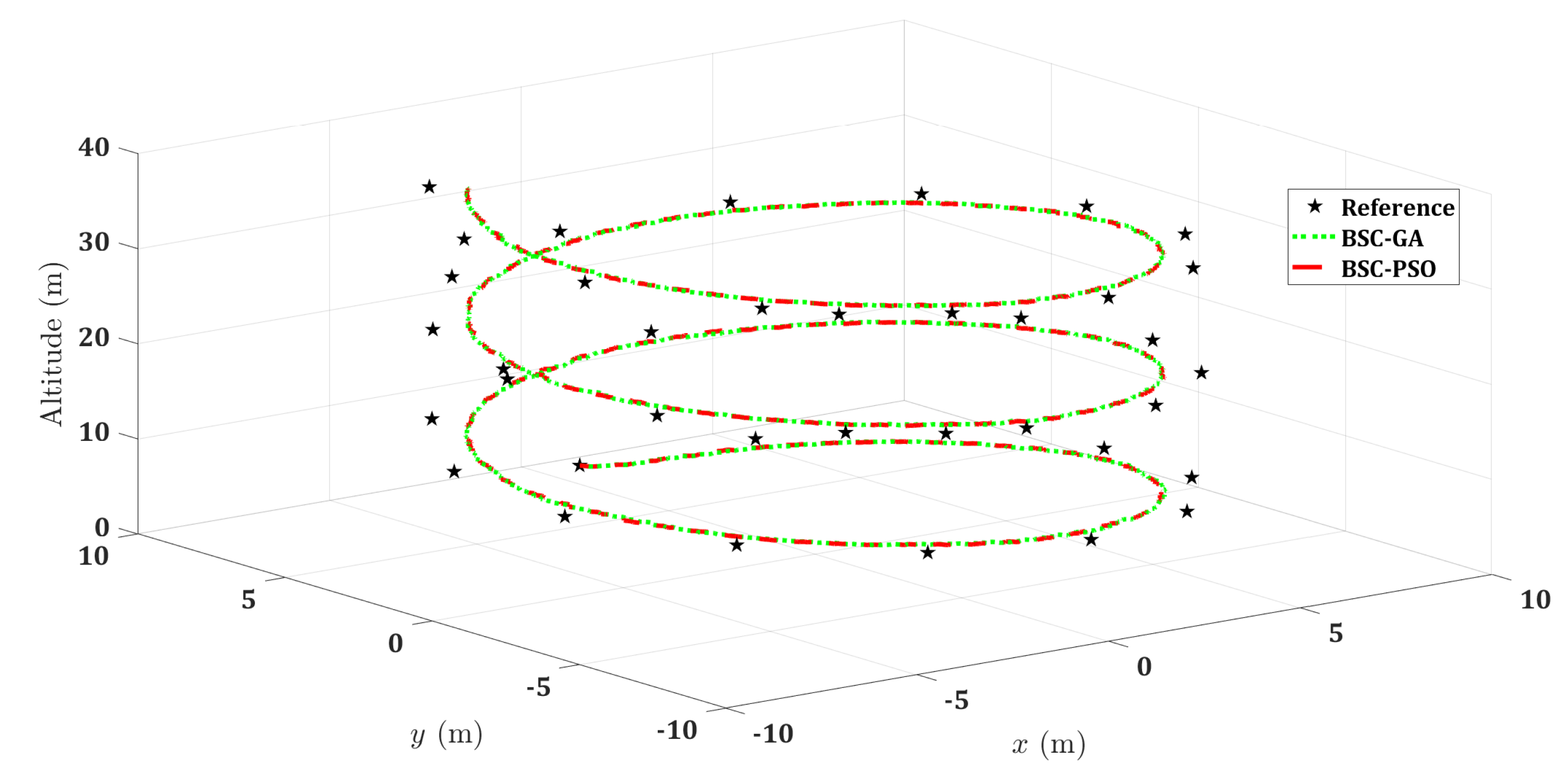
5.2. Three-Dimensional (3D) Trajectories
6. Conclusions and Future Prospects
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Stability Analysis
References
- Nguyen, N.P.; Park, D.; Ngoc, D.N.; Xuan-Mung, N.; Huynh, T.T.; Nguyen, T.N.; Hong, S.K. Quadrotor Formation Control via Terminal Sliding Mode Approach: Theory and Experiment Results. Drones 2022, 6, 172. [Google Scholar] [CrossRef]
- Farid, G.; Cocuzza, S.; Younas, T.; Razzaqi, A.A.; Wattoo, W.A.; Cannella, F.; Mo, H. Modified A-Star (A*) Approach to Plan the Motion of a Quadrotor UAV in Three-Dimensional Obstacle-Cluttered Environment. Appl. Sci. 2022, 12, 5791. [Google Scholar] [CrossRef]
- Iaboni, C.; Lobo, D.; Choi, J.W.; Abichandani, P. Event-Based Motion Capture System for Online Multi-Quadrotor Localization and Tracking. Sensors 2022, 22, 3240. [Google Scholar] [CrossRef] [PubMed]
- Paneque, J.; Valseca, V.; Martínez-de Dios, J.R.; Ollero, A. Autonomous Reactive LiDAR-based Mapping for Powerline Inspection. In Proceedings of the 2022 International Conference on Unmanned Aircraft Systems (ICUAS), Dubrovnik, Croatia, 21–24 June 2022; pp. 962–971. [Google Scholar]
- Nguyen, D.D.; Rohacs, J.; Rohacs, D. Autonomous Flight Trajectory Control System for Drones in Smart City Traffic Management. ISPRS Int. J. Geo-Inf. 2021, 10, 338. [Google Scholar] [CrossRef]
- Hegde, A.; Ghose, D. Multi-Quadrotor Distributed Load Transportation for Autonomous Agriculture Spraying Operations. J. Guid. Control. Dyn. 2022, 45, 944–951. [Google Scholar] [CrossRef]
- Lo, L.Y.; Yiu, C.H.; Tang, Y.; Yang, A.S.; Li, B.; Wen, C.Y. Dynamic Object Tracking on Autonomous UAV System for Surveillance Applications. Sensors 2021, 21, 7888. [Google Scholar] [CrossRef]
- Yao, Q.; Qiu, J.; Fan, Y.; Yan, W. Quad-rotor fire-fighting drone based on multifunctional integration. In Proceedings of the 2021 International Conference on Artificial Intelligence and Electromechanical Automation (AIEA), Guangzhou, China, 14–16 May 2021; pp. 70–73. [Google Scholar]
- Martinez, V. Modelling of the Flight Dynamics of a Quadrotor Helicopter. Master’s Thesis, Cranfield University, Bedford, UK, 2007; pp. 149–438. [Google Scholar]
- Hoffmann, G.; Rajnarayan, D.G.; Waslander, S.L.; Dostal, D.; Jang, J.S.; Tomlin, C.J. The Stanford testbed of autonomous rotorcraft for multi agent control (STARMAC). In Proceedings of the 23rd Digital Avionics Systems Conference, Salt Lake City, UT, USA, 28 October 2004; Volume 2. [Google Scholar]
- Rehan, M.; Akram, F.; Shahzad, A.; Shams, T.; Ali, Q. Vertical take-off and landing hybrid unmanned aerial vehicles: An overview. Aeronaut. J. 2022, 1–41. [Google Scholar] [CrossRef]
- Bouabdallah, S.; Murrieri, P.; Siegwart, R. Design and control of an indoor micro quadrotor. In Proceedings of the IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; Volume 5, pp. 4393–4398. [Google Scholar]
- Bouabdallah, S. Design and Control of Quadrotors with Application to Autonomous Flying. 2007. Available online: https://infoscience.epfl.ch/record/95939?ln=en (accessed on 30 September 2022).
- Bouabdallah, S.; Siegwart, R. Backstepping and Sliding-mode Techniques Applied to an Indoor Micro Quadrotor. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 2247–2252. [Google Scholar] [CrossRef]
- Pounds, P.; Mahony, R.; Corke, P. Modelling and control of a large quadrotor robot. Control Eng. Pract. 2010, 18, 691–699. [Google Scholar] [CrossRef]
- Pounds, P.; Mahony, R. Design Principles of Large Quadrotors for Practical Applications. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; IEEE Press: Piscataway, NJ, USA, 2009; pp. 1325–1330. [Google Scholar]
- Pounds, P.E.I. Design, Construction and Control of a Large Quadrotor Micro Air Vehicle. Ph.D. Thesis, Australian National University, Canberra, Australia, 2007. [Google Scholar]
- Pounds, P.; Mahony, R.; Hynes, P.; Roberts, J.M. Design of a four-rotor aerial robot. In The Australian Conference on Robotics and Automation; Friedrich, W., Lim, P., Eds.; Australian Robotics & Automation Association: Auckland, New Zealand, 2002; pp. 145–150. [Google Scholar]
- Kroo, I.; Kroo, P.I.; Prinz, F. The Mesicopter: A Meso-Scale Flight Vehicle—NIAC Phase II Technical Proposal; Stanford University: Stanford, CA, USA, 2001. [Google Scholar]
- Hoffmann, G.M.; Huang, H.; Waslander, S.L.; Tomlin, C.J. Quadrotor helicopter flight dynamics and control: Theory and experiment. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Hiltonhead, SC, USA, 20–23 August 2007; Volume 2, p. 4.
- Meier, L.; Tanskanen, P.; Fraundorfer, F.; Pollefeys, M. PIXHAWK: A system for autonomous flight using onboard computer vision. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2992–2997. [Google Scholar]
- How, J.P.; Behihke, B.; Frank, A.; Dale, D.; Vian, J. Real-time indoor autonomous vehicle test environment. IEEE Control Syst. 2008, 28, 51–64. [Google Scholar] [CrossRef]
- Engel, J. Autonomous Camera-Based Navigation of a Quadrocopter. Master’s Thesis, Technical University Munich, Munich, Germany, 2011. [Google Scholar]
- Spica, R.; Franchi, A.; Oriolo, G.; Bülthoff, H.H.; Giordano, P.R. Aerial grasping of a moving target with a quadrotor UAV. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 4985–4992. [Google Scholar]
- GmbH, M. 2017. Available online: https://www.microdrones.com/en/mdsolutions/mdmapper1000/ (accessed on 1 October 2022).
- Drone, P.A. 2017. Available online: https://www.parrot.com/it/droni/parrot-ardrone-20-power-edition#ar-drone-20-power-edition (accessed on 1 October 2022).
- Giernacki, W.; Kozierski, P.; Michalski, J.; Retinger, M.; Madonski, R.; Campoy, P. Bebop 2 Quadrotor as a Platform for Research and Education in Robotics and Control Engineering. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 1–4 September 2020; pp. 1733–1741. [Google Scholar]
- Ozbek, N.S.; Onkol, M.; Efe, M.O. Feedback control strategies for quadrotor-type aerial robots: A survey. Trans. Inst. Meas. Control 2016, 38, 529–554. [Google Scholar] [CrossRef]
- Goel, R.; Shah, S.M.; Gupta, N.K.; Ananthkrishnan, N. Modeling, simulation and flight testing of an autonomous quadrotor. In Proceedings of the IISc Centenary International Conference and Exhibition on Aerospace Engineering, Bangalore, India, 18–22 May 2009. [Google Scholar]
- Li, J.; Li, Y. Dynamic analysis and PID control for a quadrotor. In Proceedings of the 2011 IEEE International Conference on Mechatronics and Automation, Beijing, China, 7–10 August 2011; pp. 573–578. [Google Scholar]
- Gautam, D.; Ha, C. Control of a Quadrotor Using a Smart Self-Tuning Fuzzy PID Controller. Int. J. Adv. Robot. Syst. 2013, 10, 380. [Google Scholar] [CrossRef]
- Yang, J.; Cai, Z.; Lin, Q.; Wang, Y. Self-tuning PID control design for quadrotor UAV based on adaptive pole placement control. In Proceedings of the 2013 Chinese Automation Congress, Changsha, China, 7–8 November 2013; pp. 233–237. [Google Scholar]
- Ataka, A.; Tnunay, H.; Inovan, R.; Abdurrohman, M.; Preastianto, H.; Cahyadi, A.I.; Yamamoto, Y. Controllability and observability analysis of the gain scheduling based linearization for UAV quadrotor. In Proceedings of the 2013 International Conference on Robotics, Biomimetics, Intelligent Computational Systems, Jogjakarta, Indonesia, 25–27 November 2013; pp. 212–218. [Google Scholar]
- Amoozgar, M.H.; Chamseddine, A.; Zhang, Y. Fault-Tolerant Fuzzy Gain-Scheduled PID for a Quadrotor Helicopter Testbed in the Presence of Actuator Faults. IFAC Proc. Vol. 2012, 45, 282–287. [Google Scholar] [CrossRef]
- Sadeghzadeh, I.; Abdolhosseini, M.; Zhang, Y.M. Payload Drop Application of Unmanned Quadrotor Helicopter Using Gain-Scheduled PID and Model Predictive Control Techniques; Springer: Berlin/Heidelberg, Germany, 2012; pp. 386–395. [Google Scholar]
- Li, Y.; Yonezawa, K.; Liu, H. Effect of Ducted Multi-Propeller Configuration on Aerodynamic Performance in Quadrotor Drone. Drones 2021, 5, 101. [Google Scholar] [CrossRef]
- Mohammed, M.J.; Rashid, M.T.; Ali, A.A. Design Optimal PID Controller for Quad Rotor System. Int. J. Comput. Appl. 2014, 106, 15–20. [Google Scholar]
- Tan, C.K.; Wang, J. A novel PID controller gain tuning method for a quadrotor landing on a ship deck using the invariant ellipsoid technique. In Proceedings of the 2014 14th International Conference on Control, Automation and Systems (ICCAS 2014), Seoul, Republic of Korea, 22–25 October 2014; pp. 1339–1344. [Google Scholar]
- Nagaty, A.; Saeedi, S.; Thibault, C.; Seto, M.; Li, H. Control and Navigation Framework for Quadrotor Helicopters. J. Intell. Robot. Syst. 2013, 70, 1–12. [Google Scholar] [CrossRef]
- Argentim, L.M.; Rezende, W.C.; Santos, P.E.; Aguiar, R.A. PID, LQR and LQR-PID on a quadcopter platform. In Proceedings of the 2013 International Conference on Informatics, Electronics and Vision (ICIEV), Dhaka, Bangladesh, 17–18 May 2013; pp. 1–6. [Google Scholar]
- Zeng, Y.; Jiang, Q.; Liu, Q.; Jing, H. PID vs. MRAC Control Techniques Applied to a Quadrotor’s Attitude. In Proceedings of the 2012 Second International Conference on Instrumentation, Measurement, Computer, Communication and Control, Harbin, China, 8–10 December 2012; pp. 1086–1089. [Google Scholar]
- Li, T.; Zhang, Y.; Gordon, B.W. Passive and active nonlinear fault-tolerant control of a quadrotor unmanned aerial vehicle based on the sliding mode control technique. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2013, 227, 12–23. [Google Scholar] [CrossRef]
- Jafar, A.; Bhatti, A.I.; Ahmad, S.; Ahmed, N. Robust gain-scheduled linear parameter-varying control algorithm for a lab helicopter: A linear matrix inequality–based approach. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2018, 232, 558–571. [Google Scholar] [CrossRef]
- Faris, F.; Moussaoui, A.; Djamel, B.; Mohammed, T. Design and real-time implementation of a decentralized sliding mode controller for twin rotor multi-input multi-output system. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2017, 231, 3–13. [Google Scholar] [CrossRef]
- Mehndiratta, M.; Kayacan, E. Receding horizon control of a 3 DOF helicopter using online estimation of aerodynamic parameters. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 232, 1442–1453. [Google Scholar] [CrossRef]
- Novotňák, J.; Fiľko, M.; Lipovský, P.; Šmelko, M. Design of the System for Measuring UAV Parameters. Drones 2022, 6, 213. [Google Scholar] [CrossRef]
- Waslander, S.L.; Hoffmann, G.M.; Jang, J.S.; Tomlin, C.J. Multi-agent quadrotor testbed control design: Integral sliding mode vs. reinforcement learning. In Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 3712–3717. [Google Scholar]
- Besnard, L.; Shtessel, Y.B.; Landrum, B. Quadrotor vehicle control via sliding mode controller driven by sliding mode disturbance observer. J. Frankl. Inst. 2012, 349, 658–684. [Google Scholar] [CrossRef]
- Li, R.; Yang, L.; Chen, Y.; Lai, G. Adaptive Sliding Mode Control of Robot Manipulators with System Failures. Mathematics 2022, 10, 339. [Google Scholar] [CrossRef]
- Ullah, S.; Khan, Q.; Mehmood, A.; Kirmani, S.A.M.; Mechali, O. Neuro-adaptive fast integral terminal sliding mode control design with variable gain robust exact differentiator for under-actuated quadcopter UAV. ISA Trans. 2022, 120, 293–304. [Google Scholar] [CrossRef] [PubMed]
- Merheb, A.R.; Noura, H.; Bateman, F. Passive fault tolerant control of quadrotor UAV using regular and cascaded Sliding Mode Control. In Proceedings of the 2013 Conference on Control and Fault-Tolerant Systems (SysTol), Nice, France, 9–11 October 2013; pp. 330–335. [Google Scholar]
- Merheb, A.R.; Noura, H.; Bateman, F. Active fault tolerant control of quadrotor UAV using Sliding Mode Control. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014; pp. 156–166. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, Y.; Zhang, W. Integrated path planning and trajectory tracking control for quadrotor UAVs with obstacle avoidance in the presence of environmental and systematic uncertainties: Theory and experiment. Aerosp. Sci. Technol. 2022, 120, 107277. [Google Scholar] [CrossRef]
- Huang, S.; Yang, Y. Adaptive Neural-Network-Based Nonsingular Fast Terminal Sliding Mode Control for a Quadrotor with Dynamic Uncertainty. Drones 2022, 6, 206. [Google Scholar] [CrossRef]
- Basri, M.A.M.; Husain, A.R.; Danapalasingam, K.A. Intelligent adaptive backstepping control for MIMO uncertain non-linear quadrotor helicopter systems. Trans. Inst. Meas. Control 2015, 37, 345–361. [Google Scholar] [CrossRef]
- Abdelmaksoud, S.I.; Mailah, M.; Abdallah, A.M. Control Strategies and Novel Techniques for Autonomous Rotorcraft Unmanned Aerial Vehicles: A Review. IEEE Access 2020, 8, 195142–195169. [Google Scholar] [CrossRef]
- Silano, G.; Iannelli, L. MAT-Fly: An Educational Platform for Simulating Unmanned Aerial Vehicles Aimed to Detect and Track Moving Objects. IEEE Access 2021, 9, 39333–39343. [Google Scholar] [CrossRef]
- Kim, J.; Gadsden, S.A.; Wilkerson, S.A. A Comprehensive Survey of Control Strategies for Autonomous Quadrotors. Can. J. Electr. Comput. Eng. 2020, 43, 3–16. [Google Scholar] [CrossRef]
- Tuan, L.L.; Won, S. PID based sliding mode controller design for the micro quadrotor. In Proceedings of the 2013 13th International Conference on Control, Automation and Systems (ICCAS 2013), Gwangju, Republic of Korea, 20–23 October 2013; pp. 1860–1865. [Google Scholar]
- Szafranski, G.; Czyba, R. Different Approaches of PID Control UAV Type Quadrotor. Available online: https://repository.tudelft.nl/islandora/object/uuid:3517822b-0687-48bb-82a8-748191b97531 (accessed on 30 October 2022).
- Shepherd, J.F., III; Tumer, K. Robust neuro-control for a micro quadrotor. In Proceedings of the 12th Annual Conference on Genetic and Evolutionary Computation, Portland, OR, USA, 7–11 July 2010; ACM: New York, NY, USA, 2010; pp. 1131–1138. [Google Scholar] [CrossRef]
- Chu, H.; Jing, Q.; Chang, Z.; Shao, Y.; Zhang, X.; Mukherjee, M. Quadrotor Attitude Control via Feedforward All-Coefficient Adaptive Theory. IEEE Access 2020, 8, 116441–116453. [Google Scholar] [CrossRef]
- Moness, M.; Moustafa, A.M. Tuning a digital multivariable controller for a lab-scale helicopter system via simulated annealing and evolutionary algorithms. Trans. Inst. Meas. Control 2015, 37, 1254–1273. [Google Scholar] [CrossRef]
- Moness, M.; Abdelghany, M.B. Development and Analysis of Linear Model Representations of the Quad-Rotor System. In Proceedings of the International Conference on Aerospace Sciences and Aviation Technology, 16 (Aerospace Sciences & Aviation Technology, ASAT-16, Cairo, Egypt, 26–28 May 2015; Number 16. pp. 1–14. [Google Scholar] [CrossRef][Green Version]
- Lopez-Sanchez, I.; Montoya-Cháirez, J.; Pérez-Alcocer, R.; Moreno-Valenzuela, J. Experimental Parameter Identifications of a Quadrotor by Using an Optimized Trajectory. IEEE Access 2020, 8, 167355–167370. [Google Scholar] [CrossRef]
- Bresciani, T. Modelling, Identification and Control of a Quadrotor Helicopter. Mater’s Thesis, Department of Automatic Control, Lund University, Lund, Sweden, 2008. [Google Scholar]
- Nagaty, A.; Thibault, C.; Seto, M.; Trentini, M.; Li, H. Construction, modelling, and control of an autonomous unmanned aerial vehicle for target localization. Can. Aeronaut. Space J. 2015, 61, 23–35. [Google Scholar] [CrossRef]
- Michael, N.; Mellinger, D.; Lindsey, Q.; Kumar, V. The GRASP Multiple Micro-UAV Testbed. IEEE Robot. Autom. Mag. 2010, 17, 56–65. [Google Scholar] [CrossRef]
- Fradkov, A.L.; Miroshnik, I.V.; Nikiforov, V.O. Nonlinear and Adaptive Control of Complex Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 491. [Google Scholar]
- Das, S.; Pan, I.; Das, S.; Gupta, A. A Novel Fractional Order Fuzzy PID Controller and Its Optimal Time Domain Tuning Based on Integral Performance Indices. Eng. Appl. Artif. Intell. 2012, 25, 430–442. [Google Scholar] [CrossRef]
- Li, J.; Mao, J.; Zhang, G. Evolutionary algorithms based parameters tuning of PID controller. In Proceedings of the Control and Decision Conference (CCDC), Mianyang, China, 23–25 May 2011; pp. 416–420. [Google Scholar]
- Zhang, F.; Yang, C.; Zhou, X.; Gui, W. Fractional-order PID controller tuning using continuous state transition algorithm. Neural Comput. Appl. 2018, 29, 795–804. [Google Scholar] [CrossRef]
- Liu, Y.; Li, X.; Wang, T.; Zhang, Y.; Mei, P. Quantitative stability of quadrotor unmanned aerial vehicles. Nonlinear Dyn. 2017, 87, 1819–1833. [Google Scholar] [CrossRef]





| No. | Reference | Platform | University/Company | Year |
|---|---|---|---|---|
| 1 | [21] | PIXHAWK | ETHZ | 2011 |
| 2 | [19] | Mesicopter | Stanford | 2001 |
| 3 | [12] | OS4 | EPFL | 2004 |
| 4 | [20] | STARMAC | Stanford | 2005 |
| 5 | [22] | RAVEN | MIT | 2008 |
| 6 | [15] | X4 Flyer | ANU | 2008 |
| 7 | [23] | MAVs | TUM | 2012 |
| 8 | [24] | GRASP | GRASP team | 2012 |
| 9 | [25] | Parrot AR.DRONE | French company Parrot | 2016 |
| 10 | [26] | mdMAPPER1000 | German company MICRODRONES | 2017 |
| 11 | [27] | FlyBebop | Poznan University of Technology | 2020 |
| Controller | ||||
|---|---|---|---|---|
| Reference | Platform | Approach | Tuning Method | Controller Target |
| [59] | PIXHAWK | PID + SMC | EKF | Localization |
| [39] | COBRA | PID + BSC | Gazebo | Navigation |
| [60] | LinkQuad | PID, LQR, PID + LQR | ITAE, LQR loop | Robustness |
| [61] | MAV | PID | Neural network | Disturbance rejection |
| [28] | QR-UAV | SMC and BSC | FLC | Payload dropping |
| [14] | OS4 | SMC and BSC | NCD | Stabilzation |
| [47] | STARMAC | SMC and ISMC | MBRL | Outdoor control |
| [51,52] | standard | PF-SMC and AF-SMC | ESA and BSSA | Stablization and navigation |
| [55] | MIMO-quadrotor | PF-SMC and AF-SMC | ESA and RBFNN | Trajectory tracking missions |
| [62] | simulation | Feedforward-adaptive control theory | Adaptive laws | Attitude control |
| Algorithm | Parameter | Value |
|---|---|---|
| Population size | 50 | |
| Generation | * 100 | |
| Elite count | ||
| GA | Crossover fraction | |
| Migration fraction | ||
| Migration interval | 20 | |
| Function tolerance | ||
| Swarm size | * 10 | |
| Max iteration | * 200 | |
| MPSO | Min fraction neighbors | |
| Initial swarm span | 2000 | |
| Function tolerance |
| Population Size | Crossover Fraction | Best PI | Mean PI | Standard Deviation | Average FEC | Average CT (min) |
|---|---|---|---|---|---|---|
| 80 | 0.6 | 1.216228 | 1.277688 | 0.056627 | 4080 | 7.50 |
| 80 | 0.7 | 1.087693 | 1.191613 | 0.096759 | 4080 | 8.57 |
| 80 | 0.8 | 1.192226 | 1.305917 | 0.068377 | 4080 | 10.66 |
| 80 | 0.9 | 1.157399 | 1.281824 | 0.091529 | 4080 | 8.55 |
| 120 | 0.6 | 1.179078 | 1.312724 | 0.103165 | 6120 | 11.03 |
| 120 | 0.7 | 1.259124 | 1.298816 | 0.037556 | 6120 | 11.22 |
| 120 | 0.8 | 1.195250 | 1.286108 | 0.108280 | 6120 | 10.47 |
| 120 | 0.9 | 1.178229 | 1.254034 | 0.064195 | 6120 | 10.26 |
| 160 | 0.6 | 1.243172 | 1.360126 | 0.074655 | 8160 | 13.70 |
| 160 | 0.7 | 1.173221 | 1.268387 | 0.071414 | 8160 | 13.79 |
| 160 | 0.8 | 1.119076 | 1.449619 | 0.605782 | 8160 | 13.73 |
| 160 | 0.9 | 1.080213 | 1.219144 | 0.090415 | 8160 | 13.75 |
| Variable | Description | Value |
|---|---|---|
| Mass of the quadrotor | 1.006 kg | |
| g | Gravitational acceleration | 9.81 ms |
| l | Moment arm length | 0.225 m |
| Moment of inertia along x | 0.0143 kgm | |
| Moment of inertia along y | 0.0148 kgm | |
| Moment of inertia along z | 0.0246 kgm | |
| Thrust factor | Ns | |
| Drag factor | Nms | |
| Rotor inertia | kgm |
| Best | Mean | Standard | Average | Rise Time | Overshoot | Settling Time | |
|---|---|---|---|---|---|---|---|
| Objective Function | Objective Function | Deviation | Computing Time (min) | (s) | % | (s) | |
| PD-GA | 3.89187 | 3.90278 | 0.01139 | 10.02 | 0.061 | 0 | 0.111 |
| PD-PSO | 3.89206 | 3.89762 | 0.00723 | 1.93 | 0.061 | 0 | 0.111 |
| BSC-GA | 2.55844 | 2.5618 | 0.00324 | 7.56 | 0.051 | 0 | 0.094 |
| BSC-PSO | 2.56584 | 2.56717 | 0.00134 | 3.7 | 0.052 | 0 | 0.094 |
| SM-GA | 10.13309 | 11.57198 | 1.87204 | 11.21 | 0.138 | 0 | 0.241 |
| SM-PSO | 10.22139 | 11.14991 | 1.06096 | 7.67 | 0.138 | 0 | 0.241 |
| Best | Mean | Standard | Average | Rise Time | Overshoot | Settling Time | |
|---|---|---|---|---|---|---|---|
| Objective Function | Objective Function | Deviation | Computing Time (min) | (s) | % | (s) | |
| PD-GA | 3.89187 | 3.90278 | 0.01139 | 19.34 | 0.061 | 0 | 0.111 |
| PD-PSO | 3.89206 | 3.89762 | 0.00723 | 3.89 | 0.061 | 0 | 0.111 |
| BSC-GA | 2.55844 | 2.5618 | 0.00324 | 15.89 | 0.051 | 0 | 0.094 |
| BSC-PSO | 2.56584 | 2.56717 | 0.00134 | 3.99 | 0.052 | 0 | 0.094 |
| SM-GA | 10.13309 | 11.57198 | 1.87204 | 11.22 | 0.138 | 0 | 0.241 |
| SM-PSO | 10.22139 | 11.14991 | 1.06096 | 7.69 | 0.138 | 0 | 0.241 |
| Best | Mean | Standard | Average | Rise Time | Overshoot | Settling Time | |
|---|---|---|---|---|---|---|---|
| Objective Function | Objective Function | Deviation | Computing Time (min) | (s) | % | (s) | |
| PD-GA | 39.55843 | 41.58047 | 0.85551 | 8.91 | 0.189 | 0 | 0.337 |
| PD-PSO | 39.43105 | 39.79369 | 1.00944 | 4.66 | 0.189 | 0 | 0.326 |
| BSC-GA | 39.569 | 39.57475 | 0.00631 | 6.45 | 0.198 | 0 | 0.355 |
| BSC-PSO | 39.57773 | 39.5853 | 0.00373 | 4.28 | 0.196 | 0 | 0.351 |
| SM-GA | 52.65907 | 55.06883 | 3.28271 | 4.93 | 0.328 | 0.4 | 0.514 |
| SM-PSO | 52.75427 | 53.77765 | 0.74082 | 3.98 | 0.314 | 0.1 | 0.508 |
| Best | Mean | Standard | Average | Rise Time | Overshoot | Settling Time | |
|---|---|---|---|---|---|---|---|
| Objective Function | Objective Function | Deviation | Computing Time (min) | (s) | % | (s) | |
| PD-GA | 916.05901 | 916.05954 | 0.00051 | 6.24 | 0.461 | 5.9 | 1.142 |
| PD-PSO | 916.06168 | 916.0893 | 0.04788 | 1.92 | 0.461 | 5.9 | 1.142 |
| BSC-GA | 550.49708 | 551.42031 | 2.44355 | 4.34 | 0.466 | 6.5 | 1.184 |
| BSC-PSO | 550.49708 | 550.56088 | 0.08678 | 2.44 | 0.466 | 6.5 | 1.184 |
| SM-GA | 793.10311 | 888.21495 | 111.88848 | 6.14 | 0.754 | 0 | 1.464 |
| SM-PSO | 797.4567 | 823.99621 | 19.36555 | 1.85 | 0.756 | 0 | 1.464 |
| Attitude Control | Heading Control | Altitude Control | Position Control | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PD-GA | 100 | 3.21 | 100 | 3.21 | 7.76 | 0.86 | 100 | 20.84 | 10.12 | 5.97 | 10.61 | 6.07 |
| PD-PSO | 100 | 3.21 | 100 | 3.21 | 6.59 | 0.75 | 100 | 20.84 | 10.06 | 5.92 | 11.98 | 6.60 |
| Attitude Control | Heading Control | Altitude Control | Position Control | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SMC-GA | 92.59 | 72.72 | 92.59 | 72.72 | 17.44 | 17.16 | 100 | 5.15 | 11 | 6.60 | 11.39 | 6.60 |
| SMC-PSO | 90.26 | 96.37 | 70.26 | 96.37 | 18.11 | 17.04 | 5.15 | 100 | 10.56 | 6.25 | 11.88 | 6.87 |
| Attitude Control | Heading Control | Altitude Control | Position Control | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BSC-GA | 13.98 | 99.29 | 13.98 | 99.29 | 3.77 | 18.22 | 3.18 | 68.02 | 7.43 | 4.57 | 8.91 | 5.08 |
| BSC-PSO | 13.99 | 100 | 13.99 | 100 | 4.09 | 20.79 | 3.17 | 49.06 | 6.80 | 4.35 | 8 | 4.71 |
| x | y | z | |||||||
|---|---|---|---|---|---|---|---|---|---|
| MSE | NRMSE | Goodness | MSE | NRMSE | Goodness | MSE | NRMSE | Goodness | |
| % | % | % | % | % | % | ||||
| PD-GA | 0.0009 | 0.73 | 99.27 | 0.0012 | 1.66 | 98.34 | 0.0097 | 1.13 | 97.72 |
| PD-PSO | 0.0009 | 0.74 | 99.26 | 0.0009 | 1.48 | 98.52 | 0.0097 | 1.13 | 97.72 |
| BSC-GA | 0.0068 | 2.04 | 97.96 | 0.0273 | 8.61 | 91.39 | 0.0014 | 0.43 | 99.12 |
| BSC-PSO | 0.0074 | 2.12 | 97.88 | 0.0246 | 8.14 | 91.86 | 0.0014 | 0.43 | 99.12 |
| SMC-GA | 0.0016 | 0.96 | 99.04 | 0.0011 | 1.63 | 98.37 | 0.0029 | 0.61 | 98.76 |
| SMC-PSO | 0.0018 | 1.02 | 98.98 | 0.0014 | 1.78 | 98.22 | 0.0029 | 0.62 | 98.75 |
| x | y | z | |||||||
|---|---|---|---|---|---|---|---|---|---|
| MSE | NRMSE | Goodness | MSE | NRMSE | Goodness | MSE | NRMSE | Goodness | |
| % | % | % | % | % | % | ||||
| PD-GA | 0.0188 | 2.45 | 97.55 | 0.0156 | 2.29 | 97.71 | 0.0098 | 0.44 | 99.05 |
| PD-PSO | 0.0191 | 2.47 | 97.53 | 0.012 | 2 | 98 | 0.0098 | 0.44 | 99.05 |
| BSC-GA | 0.3168 | 10.87 | 89.13 | 0.289 | 10.64 | 89.34 | 0.0016 | 0.18 | 99.61 |
| BSC-PSO | 0.3353 | 11.21 | 88.78 | 0.2643 | 10.13 | 89.85 | 0.0016 | 0.18 | 99.61 |
| SMC-GA | 0.0016 | 0.71 | 99.29 | 0.0012 | 0.61 | 99.39 | 0.0089 | 0.42 | 99.09 |
| SMC-PSO | 0.0019 | 0.75 | 99.25 | 0.0014 | 0.67 | 99.33 | 0.0089 | 0.42 | 99.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelghany, M.B.; Moustafa, A.M.; Moness, M. Benchmarking Tracking Autopilots for Quadrotor Aerial Robotic System Using Heuristic Nonlinear Controllers. Drones 2022, 6, 379. https://doi.org/10.3390/drones6120379
Abdelghany MB, Moustafa AM, Moness M. Benchmarking Tracking Autopilots for Quadrotor Aerial Robotic System Using Heuristic Nonlinear Controllers. Drones. 2022; 6(12):379. https://doi.org/10.3390/drones6120379
Chicago/Turabian StyleAbdelghany, Muhammad Bakr, Ahmed M. Moustafa, and Mohammed Moness. 2022. "Benchmarking Tracking Autopilots for Quadrotor Aerial Robotic System Using Heuristic Nonlinear Controllers" Drones 6, no. 12: 379. https://doi.org/10.3390/drones6120379
APA StyleAbdelghany, M. B., Moustafa, A. M., & Moness, M. (2022). Benchmarking Tracking Autopilots for Quadrotor Aerial Robotic System Using Heuristic Nonlinear Controllers. Drones, 6(12), 379. https://doi.org/10.3390/drones6120379






