Multidisciplinary Analysis and Optimization Method for Conceptually Designing of Electric Flying-Wing Unmanned Aerial Vehicles

Abstract

Current unmanned aerial vehicles have been designed by applying the traditional approach to aircraft conceptual design which has drawbacks in terms of the individual analysis of each discipline involved in the conception of new aircraft, the reliance on the designer’s experience and intuition, and the inability of evaluating all possible design solutions. Multidisciplinary analysis and optimization focus on solving these problems, by synthesizing all the disciplines involved and accounting for their mutual interaction. This study presents a multidisciplinary analysis and optimization method for conceptually designing electrical flying-wing micro-unmanned aerial vehicles. The conceptual design task was formulated as a non-linear mathematical programming problem. The method considers the trimming of the UAV during each mission profile phase, consisting of the climb, cruise, and descent. We used two algorithms, one for design space exploration and another for optimization. Typical examples of solving conceptual design problems were considered in the work: the modernization of an existing UAV; the effect of the change of the payload and endurance change on the takeoff weight; and the influence of different static margins on aerodynamic characteristics. The advantages of using this design method are the remotion of additional internal cycles to solve the sizing equation at each optimization step, and the possibility of not only obtaining a unique optimal solution but also a vector of optimal solutions.

1. Introduction

Unmanned aerial vehicles (UAVs) have been an object of interest since the early years of aviation [1,2,3], but they have only recently become widely used. The interest in this aircraft resides in their implementation in either low human interventions or complete human exclusion tasks. For instance, in traffic monitoring [4,5,6], infrastructure monitoring [7,8], environmental monitoring [9,10,11], and surveillance [12,13,14], UAVs are employed because they require long periods of activity and direct human intervention is limited. Agriculture [15,16,17], terrain mapping [18], and data collection (gathering) are examples of tasks in which the use of UAV cuts operational costs, along with military applications [14], emergency rescue, and natural disaster tasks [19,20], in which the deployment of UAVs is in preference due to the dangerous nature of the performed tasks.

Regardless of the task, the search for a design configuration and parameters that fulfill requirements is the priority and is accomplished during the conceptual design phase. Even though during this phase the time consumption and cost are less than the whole design process, many tasks must be completed, and many important decisions must be taken. Several authors have reported the importance of this design phase [21,22,23,24,25,26]; for example, it is estimated that up to 80% of the costs of an aircraft’s life cycle are determined during the conceptual and preliminary design phase [27], reminding us of the importance of this phase. Conceptual aircraft design has seen different approaches. First, they were designed by trial and error. Then, after gathering enough information, a statistical methodology was developed, which is based on empirical data from existing aircraft. This has been the traditional design paradigm until today and has been adequate for past demands. Examples of this design paradigm are found in the literature [21,22,23,24,25,28,29,30]. The methods and approaches founded on these studies are primarily based on empirical formulas, decoupling of the involved disciplines for separated analysis, a sequential approach which converges by iteration, and, more importantly, on the designer’s experience and intuition. To illustrate this, the studies [31,32,33,34] are related to the design of UAVs by applying the traditional design paradigm. Other works present a slightly different method for conceptual design. For instance, in work [35], a method for the conceptual design of small aircraft with hybrid-electric propulsion systems was proposed by adapting the existing methods. Similarly, [36] proposed the use of neural networks as a surrogate model, due to the high computational requirements required by the genetic algorithm used for the optimization of the wing geometry. Another example was presented in [37], in which not only genetic algorithms were used, but also differential evolution algorithms for performing multi-objective optimization.

However, current needs demand more efficient aircraft [38]; hence, new methods for aircraft design are required. Concurrent design is a design paradigm aimed at significantly reducing product development time and optimizing product performance, which has been gradually replacing the traditional design paradigm [39,40]. One of the main methodologies of concurrent design is multidisciplinary analysis and optimization (MDAO), a new physics-based design methodology which considers the relation between disciplines involved in aircraft design, has been widely applied to aircraft design [41,42,43,44,45,46,47,48], and lately, to the design of UAVs. For example, in [49], an MDAO-based methodology for designing an electric UAV, which optimizes aerodynamic configurations and propulsion systems, was presented; or in [50], which performed a multi-objective MDAO for maximizing both the payload weight and cruise duration of a tail-sitter UAV.

Nevertheless, the presented works regarding conceptual fixed-wing UAV design have shown some limitations [31,32,33,36,37,49,50]: for instance, the optimization process does not consider any stability or control constraints [34,49,51] (which are especially important in flying wing configurations); the optimization does not contemplate a whole mission profile [34,36,50,51]; the optimization approach converges to a local minimum [49]; an optimization algorithm was not even considered [32,33,34,35].

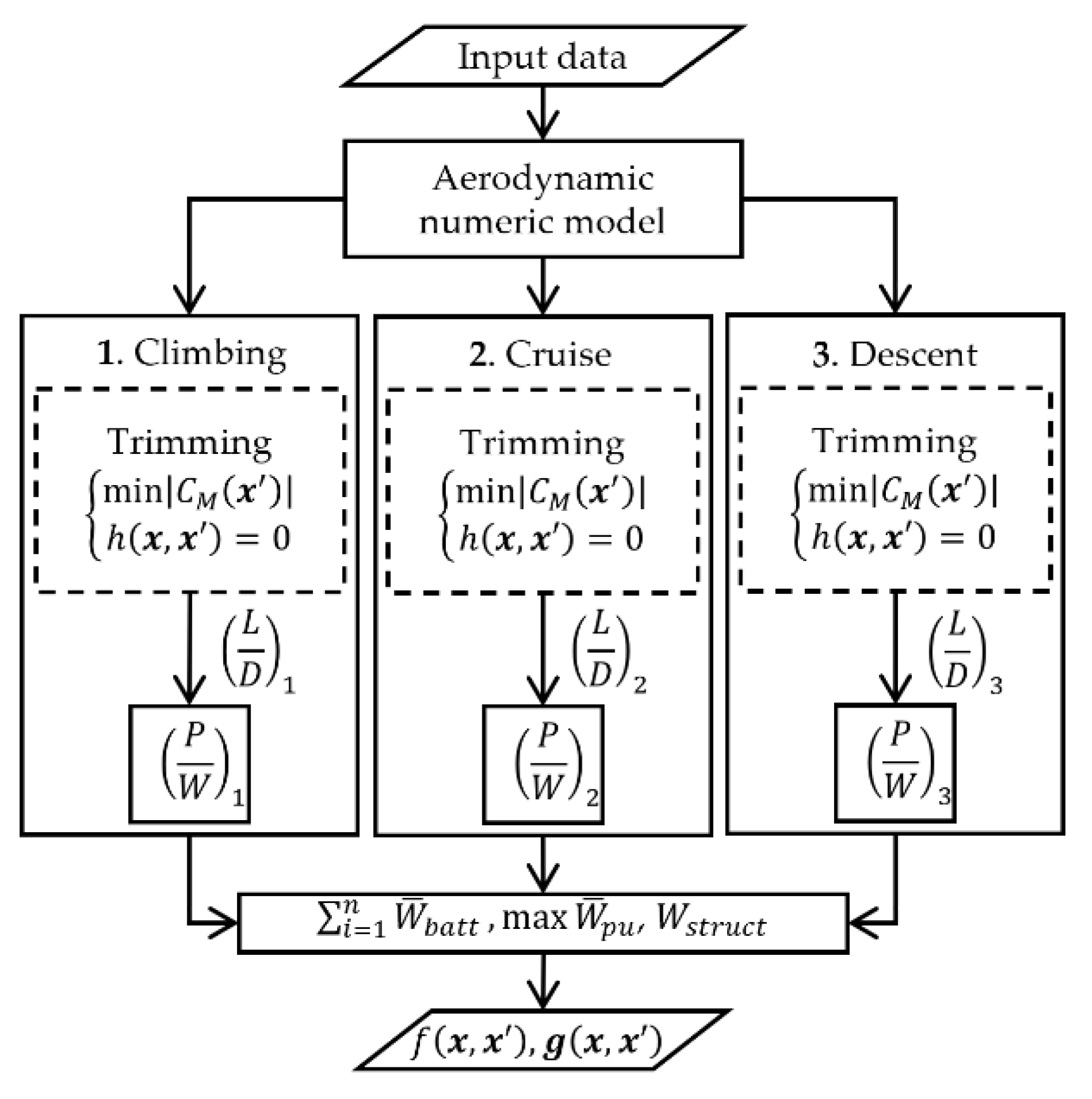
In this paper, we present an MDAO design method for electric propulsion flying wing UAVs. Aerodynamics, stability and control, propulsion, and weight and balance were the disciplines considered in the conceptual phase. The objective of the current work was to further increase the model fidelity at the conceptual design level, without compromising the design time. This was accomplished by introducing a trimming procedure during the analysis of the mission profile stage, which considers the aircraft pitch angle by performing penalty-based optimization for minimizing the maximum take-off weight (MTOW), varying geometrical and flight conditions parameters subject to stability, balance, aerodynamic constraints, by solving the sizing equation, and reducing the population size within the optimization for reducing the computational time.

The advantages of using this method in design are the remotion of additional internal cycles to solve the sizing equation at each optimization step; the possibility of not only obtaining the single optimal solution, but also the optimal solution vector, the ability to perform a rapid study of the impact of various parameters and flight conditions on flight performance and technical indicators, while ensuring a sufficiently detailed view of the aircraft designed considering the aircraft trimming, given the static margin, as well as the requirements of pitch control.

2. Materials and Methods

The problem of selecting the optimal parameters of an electric flying wing UAV was formulated in terms of non-linear mathematical programming:

• minimize          f(x)
• by varying        ${\underset{¯}{\mathrm{x}}}_{\mathrm{I}}$ ≤ x_i ≤ ${\overline{\mathrm{x}}}_{\mathrm{I}}$       i = 1, …, n_x
• subject to          g_j(x) ≤ 0            j = 1, …, n_g
•          h_l(x) = 0            l = 1, …, n_h

The MTOW W₀ was chosen as the objective function. The design variables were the aspect ratio AR, leading-edge sweep angle Λ_LE, taper ratio λ, geometric twist τ, wing loading ^W/_S, flight speed v, the first coefficient of the polynomial of the camber line C, the angle of attack α, and the static margin (${\overline{\mathrm{x}}}_{\mathrm{CG}}$ − ${\overline{\mathrm{x}}}_{\mathrm{AC}}$). The proposed method allowed for the consideration of other types and a number of design variables. However, emphasis was placed on these parameters, as they have the greatest influence on the flight and energetic characteristics of small electric UAVs. The constraints were as follows:

• Zero longitudinal momentum to trim the aircraft, considering the given static margin;
• The constraint on the maximum lift coefficient value;
• An inequality constraint on the minimum relative elevon moment arm value to ensure enough UAV pitch control;
• The equality constraint on the value of the lift coefficient required to ensure horizontal flight.

The objective function, as well as the constraints, are presented as follows:

$$\mathrm{f}(\mathbf{x},\mathbf{x}’)={\mathrm{W}}_0(\mathbf{x},\mathbf{x}’)$$

$${\mathrm{g}}_1(\mathbf{x}\mathbf{’})=\left|{\mathrm{C}}_{\mathrm{M}}\right(\mathbf{x}\mathbf{’}\left)\right|-{\delta }_{\mathrm{CM}}\le 0$$

$${\mathrm{g}}_2\left(\mathbf{x}\right)={\mathrm{C}}_{\mathrm{L}}\left(\mathbf{x}\right)-{\mathrm{C}}_{\mathrm{L\; max}}\le 0$$

$${\mathrm{g}}_3\left(\mathbf{x}\right)={\mathrm{f}}_{\mathrm{pc}}\mathrm{AR}-{\overline{\mathrm{l}}}_{\mathrm{el}}\le 0$$

$$\mathrm{h}(\mathbf{x}\mathbf{,}\mathbf{x}\mathbf{’})={\mathrm{C}}_{\mathrm{L\; eq}}(\mathbf{x}\mathbf{’})-{\mathrm{C}}_{\mathrm{L}}\left(\mathbf{x}\right)\le 0$$

where: x = [AR, Λ, λ, θ, ^W/_S, V] and x’ = [C, α, (${\overline{\mathrm{x}}}_{\mathrm{CG}}$ − ${\overline{\mathrm{x}}}_{\mathrm{AC}}$)] are the design variables vector; C_M is the pitching moment coefficient; δ_CM is the pitch coefficient threshold; C_L is the lift coefficient; C_{L max} is the maximum lift coefficient; f_pc is the fudge factor for pitch control; ${\overline{\mathrm{l}}}_{\mathrm{el}}$ is the relative elevon moment arm; C_{L eq} is the trimming lift coefficient.

The method relies on 2 main steps:

• Calculation of the objective function and constraints values.
• Solution of the optimization problem.

The objective function and the constraints calculation process is presented in Figure 1.

2.1. Calculation of the Objective Function

The sizing equation used for calculating the MTOW was the following:

$${\mathrm{W}}_0=\frac{{\mathrm{W}}_{\mathrm{payload}}+{\mathrm{W}}_{\mathrm{equip}}+{\mathrm{W}}_{\mathrm{struct}}+{\mathrm{W}}_{\mathrm{reserve}}}{1-\left(\underset{\mathrm{i}}{\max }\left(\frac{{\mathrm{W}}_{\mathrm{pu}}}{{\mathrm{W}}_0}\right)+{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}\left(\frac{{\mathrm{W}}_{\mathrm{batt}}}{{\mathrm{W}}_0}\right)\right)},$$

(1)

where the absolute weights in kg been the payload W_payload, equipment W_equip, structure W_struct, and reserve weight W_reserve are represented in the numerator, while the weight ratios been the power unit ^Wpu/_W0 and batteries weight ratio ^Wbatt/_W0 are in the numerator; i is the flight phase.

Mathematical models for determining the energy carrier weight of the batteries are different from those for determining the fuel weight of aircraft with a heat engine. For designing aircraft with electric propulsion systems, the battery weight ratio was calculated as the ratio of specific energy consumption SEC to the specific energy of battery E. The power unit weight ratio was calculated as the product of the engine weight-to-thrust (^W/_P)_pu by the power-to-weight ratio ^P/_W, thus

$$\frac{{\mathrm{W}}_{\mathrm{batt}}}{{\mathrm{W}}_0}=\mathrm{g}\frac{1}{{\mathsf{\eta }}_{\mathrm{pu}}\mathrm{SoC}}\frac{\mathrm{SEC}}{\mathrm{E}},$$

(2)

$$\frac{{\mathrm{W}}_{\mathrm{pu}}}{{\mathrm{W}}_0}={\left(\frac{\mathrm{W}}{\mathrm{P}}\right)}_{\mathrm{pu}}\frac{\mathrm{P}}{\mathrm{W}},$$

(3)

where $\mathrm{SEC}=\frac{\mathrm{P}}{\mathrm{W}}\mathrm{t}$ in kWh/kg; η_pu is the power unit efficiency; SoC is the battery state of charge; g is the Earth’s gravitational acceleration in m/c².

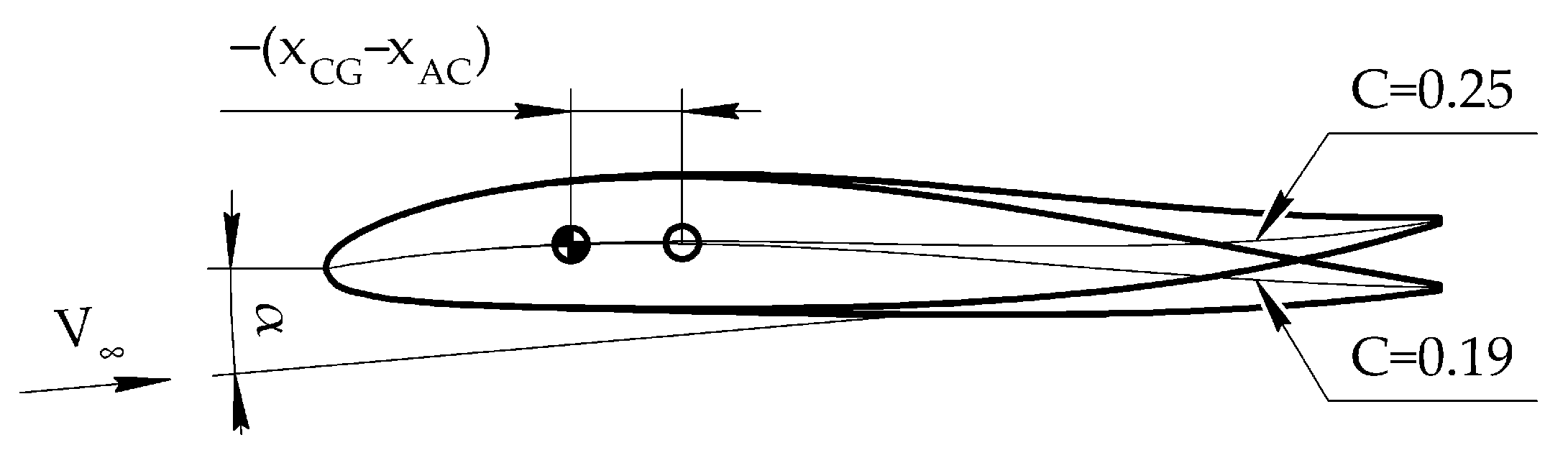
The battery and power unit weight ratio depend on the power-to-weight ratio, which was calculated by solving the flight equilibrium equations with respect to and normal to the flight path:

$$\begin{array}{c}\mathrm{T}cos\mathsf{\alpha }-\mathrm{D}-\mathrm{W}\sin \gamma =0,\\ \mathrm{L}-\mathrm{W}cos\mathsf{\gamma }+\mathrm{T}\sin \mathsf{\alpha }=0.\end{array}$$

(4)

where T is the thrust in N; D is the drag force; W is the UAV’s weight; L is the lift force; α is the angle of attack; γ is the flight path angle.

Obtained from the analysis of the free body diagram shown in Figure 2.

The power-to-weight ratio can be written as (^P/_W) = ^T/_W V, then the equation for the required power-to-weight ratio considering the propeller efficiency became:

$$\left(\frac{\mathrm{P}}{\mathrm{W}}\right)=\frac{\mathrm{V}}{{\mathsf{\eta }}_{\mathrm{prop}}}\frac{\left(\left(\frac{\mathrm{L}}{\mathrm{D}}\right)\sin \mathsf{\gamma }+\cos \mathsf{\gamma }\right)}{\left(\sin \mathsf{\alpha }+\left(\frac{\mathrm{L}}{\mathrm{D}}\right)\cos \mathsf{\alpha }\right)},$$

(5)

The power-to-weight ratio depends on the aerodynamic efficiency, and for its determination AVL [52], a vortex lattice method was used to calculate the lift and inductive wing drag, and empirical formulas were used for calculating the parasite drag [53].

For small/mini-UAVs, the weight of the flying wing structure primarily depends on the manufacturing technology, more than on its strength. Hence, the following equation, depending primarily on the area and material of the wing, was used for its calculation:

W_struct = 2 kρδS,

(6)

where: k is a coefficient accounting for the manufacture; ρ is the density of the material; δ is the thickness of the layer; S is the wing area.

The payload, equipment, and reserve weight were considered fixed weights. Therefore, their value depends exclusively on the value assigned by the designer.

2.2. Calculation of the Constraints

The calculation of the terms of the sizing equation is performed when the UAV is trimmed. The trimming of the flying wing UAV can be ensured by two parameters: the angle of attack and the airfoil shape; both parameters influence the lift and pitching moment coefficients.

The baseline airfoil was the NACA M6, modeled by a similar method of the combination of camber lines and thickness distributions. The third-order polynomial y_c = ax³ − bx² + cx, describes the airfoil. The coefficient a of the polynomial of the camber line is responsible for determining the degree of bending in its tail.

Trimming the aircraft, with respect to the UAV center of gravity ${\overline{\mathrm{x}}}_{\mathrm{CG}}$ and the given static margin, was performed by changing the coefficient C of the camber line and the angle of attack (see Figure 3). The trimming was formulated as the following optimization problem within the main optimization (see Figure 1):

• minimize        f(x’) = |C_M(x’)|
• by varying      0.19 ≤ C ≤ 0.29
•       −10 ≤ α ≤ 10
• subject to        h(x, x’) = C_{L eq}(x’) − C_L(x)cos γ = 0

The optimization problem was solved using the COBYLA method, which was applied using the Python package OpenMDAO [54].

The maximum lift coefficient of the wing was limited to 0.35, recommended for flying wing configurations.

The constraint of the relative elevon arm was formulated by statistical analysis and limited to 20% of the aspect ratio. It was formulated as follows and is geometrically presented in Figure 4.

$${\overline{\mathrm{L}}}_{\mathrm{el}}\ge 0.2\mathrm{AR},$$

(7)

$$\overline{{\mathrm{l}}_{\mathrm{el}}}=\frac{{\mathrm{l}}_{\mathrm{el}}}{\mathrm{MAC}}=\frac{{\mathrm{x}}_{\mathrm{AC}\mathrm{el}}-{\mathrm{x}}_{\mathrm{CG}}}{\mathrm{MAC}}$$

where x_AC is the position of the elevon aerodynamic center in m.

The elevon occupies the relative area bounded from 0.8 to 1 along the chord. The elevon aerodynamic center was located at 85% along the semi-wingspan.

2.3. Metrics

The aircraft mass growth factor k_MGW [55,56] is defined as

k_MGW = ¹/_Wpayload,

(8)

and is used for assessing the design solutions, i.e., the weight efficiency of the evaluated design.

2.4. Optimization Methods

In this paper, two optimization methods, the stationary Gauss-Seidel method and a differential evolutionary algorithm based on penalty functions, were used for design space exploration and minimization of the objective function, respectively.

The Gauss-Seidel method is written as:

u^(k+1) = u^(k)+E⁻¹ r(u^(k)),

(9)

where r(u^(k)) = b + Au^(k) is the residual vector; E⁻¹ is the lower triangular matrix; u^(k) = [x^(k), m₀⁰] is the parameters vector.

The Gauss-Seidel method was used along with the response surface method for design space exploration. First, the objective function was calculated for a pair of parameter vectors, while the rest of the parameters remain unchanged. Second, the response surface was constructed. Third, the minimum objective function was calculated from the obtained response surface, and the pair of parameters corresponding to this minimum was now fixed while the next iteration was performed for a new pair of parameters. The algorithm for minimizing the objective function using the Gauss-Seidel method, along with the response surface method, is presented in Figure 5.

Alternatively, a differential evolutionary algorithm based on penalty functions was proposed to increase the objective function probability to reach the global minimum. The penalty-based function is formulated as follows:

• minimize        L(x)
• by varying      x

The adaptative penalty function was taken from [57]:

$$\mathrm{L}\left(x,\mathrm{R}\right)=\left\{\begin{array}{c}f\left(x\right)\\ \psi \left(x\right)+{\mathrm{U}}_{\ast }\\ \psi \left(x\right)+f\left(x\right)\end{array}\right.\begin{array}{c}\mathrm{if}\\ \mathrm{if}\\ \mathrm{if}\end{array}\begin{array}{c}\mathsf{\psi }\left(x\right)=0\mathrm{and}\mathrm{f}\left(x\right)\le {\mathrm{U}}_{\ast }\\ \mathsf{\psi }\left(x\right)>0\mathrm{and}\mathrm{f}\left(x\right)\le {\mathrm{U}}_{\ast }\\ \mathsf{\psi }\left(x\right)>0\mathrm{and}\mathrm{f}\left(x\right)\ge {\mathrm{U}}_{\ast }\end{array}$$

(10)

where: $\mathsf{\psi }\left(x\right)={\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{m}}\max \left[0,{\mathrm{g}}_{\mathrm{j}}\left(x\right)\right]$; f(x) is objective function; g_j(x) is inequality constraint; U_* is an upper bound on the constrained global minimum value.

The value of U_* is provided by the user. In our method, U_* corresponds to 15 times the payload weight, which corresponds to the maximum aircraft mass growth of existing aircraft reported in [55,56].

The SHADE E-PSR evolutionary algorithm, as presented in [58], was used as the optimization algorithm, along with the exponential population size reduction method [59] for decreasing the optimization execution time.

Particular attention was given to the process of solving the sizing equation, which was directly solved in the optimization process (Figure 6) and did not require a separate cycle for its convergence. The take-off weight, as a design variable, was solved by the sizing equation with the optimization process (without the need for an extra iteration process for the equation convergence) by narrowing the upper and lower take-off parameter values after each iteration. The lower and upper take-off parameter bounds are updated to the minimum and maximum L(x) that fulfill ψ(x) = 0, or else the take-off bounds keep their previous value.

3. Verification of the MDAO Method

A mesh independence study of the vortex lattice method was performed. The variable parameters are the number of panels by semi-wingspan (from 10 to 100 in steps of five) and by chord (from 10 to 30 in steps of five). Thus, 95 types of meshes were created, ranging from coarse to dense, to ensure that the simulation results were sufficiently independent of the mesh. As a control value, the variant with the densest mesh was taken as the reference value. The result of the analysis shows that the aerodynamic results are independent of the mesh density, with a mesh consisting of thirty elements along the chord and ten along the semi-wingspan obtaining the following errors: 0.97%, 0%, and 0.88% for the lift, inductive drag, and pitching moment coefficients, respectively.

The results of the aircraft trim were verified by comparing the obtained values with the geometric solution to this problem.

Table 1. Initial optimization data.

Input Data	Value
Aspect ratio	3.3
Leading edge sweep angle, °	10
Taper ratio	0.77
Geometric twist angle, °	−1
Wing loading, daN/m2	5
Flight velocity, m/s	20
MTOW, kg	2.2

presents the input data, and

Table 2. Intervals of design variables.

Design Variable	Lower Value	Upper Value
Angle of attack, α	−20	20
Polynomial coefficient of the airfoil camber line	0.17	0.27

presents the design variables of the algorithm for trimming the flying wing UAV.

The combination that trims the aircraft has parameters α = 1.13° and C = 0.2080. The found point coincides with the point by using the COBYLA algorithm (see Figure 7). The error of the required angle of attack and the polynomial coefficient of the airfoil camber line was 0% and 0.1%, respectively.

Verification of the objective function calculation algorithm.

Table 3. Input data for calculating the objective function and constraints.

Input		Value
Mass, kg	payload	0.500
	equipment	0.150
	propeller	0.050
	reserve	0.020
Correction factor	power unit weight ratio	1.1
	structure weight	1.5
Flight endurance, h (min)	in cruise	1 (60)
	in climb	0.05 (3)
	in descent	0.10 (6)
Flight path angle, °	in cruise	0
	in climb	50
	in descent	−30
Efficiency	propeller	0.6
	engine	0.5
	batteries	0.7
Power-to-weight ratio, kWh/kg		0.3
Engine weight-to-thrust, daN/kW		0.3
Density, kg/m3	air	1.225
	material	2600
Batteries’ specific energy density, kWh/kg
Flight speed, m/c	in climb	0.9 Vcruise
	in descent	0.9 Vcruise
Number of composite laminate layers		1
Composite laminate layer thickness, mm		0.25

presents the input data for the process shown in Figure 5, calculating the objective function and constraint values.

Table 4. Intervals of design variables for calculating the objective function and constraints.

Design Variables	Lower Value	Upper Value
Aspect ratio	3	10
Leading edge sweep angle, °	0	45
Taper ratio	0.4	1
Geometric twist angle, °	−5	2
Wing loading, daN/m2	3	12
Flight velocity, m/s	10	30
Polynomial coefficient of the airfoil camber line	0.19	0.24

presents the design variable for the process shown in Figure 6.

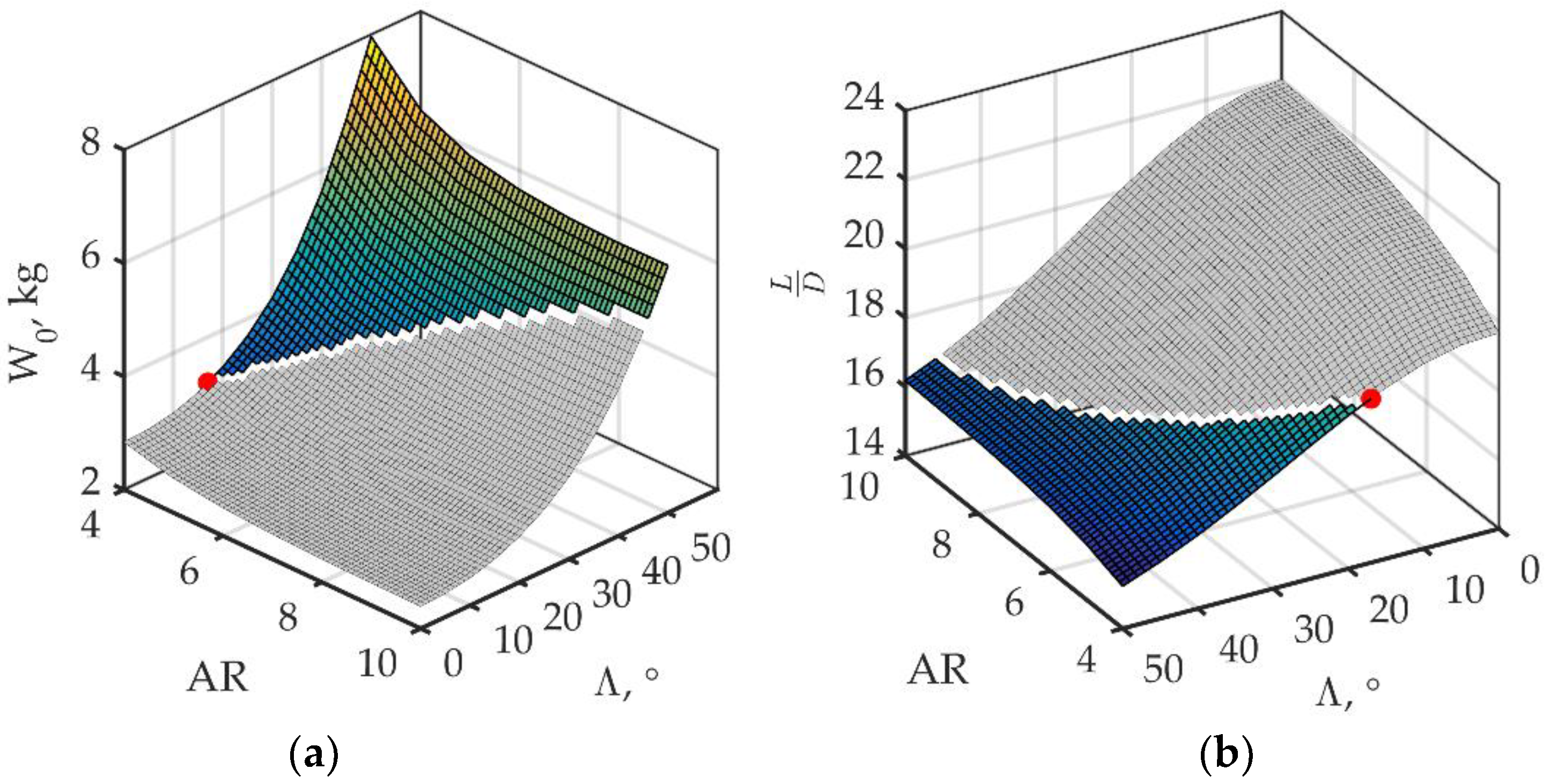
To verify the performance of the objective function calculation algorithm, the response surfaces of MTOW, the lift-to-drag ratio from aspect ratio and leading-edge sweep angle (see Figure 8a), and the specific wing loading and cruise speed (see Figure 8b) at other “frozen” parameters were plotted. The intervals at which the target function has been calculated are for aspect ratio, from 4 to 10; leading-edge sweep angle, from 0 to 50; wing loading, from 3 to 10 daN/m²; and cruise speed, from 10 to 30 m/s. Figure 8b shows the response surfaces at a specific wing loading of 6 daN/kg and a cruise speed of 20 m/s.

The area of the feasible solution is represented by colors. The part of the surface marked in gray does not fall within the area of feasible values according to the presented constraints.

For the given initial data, the most suitable combination of the two parameters is AR = 4 and Λ = 17. The MTOW is 3.202 kg, and the lift-to-drag ratio is 18.75. It should be said that the solution satisfying the minimum MTOW and maximum ^L/_D exists for the same combination of these parameters. This circumstance is characteristic of small UAVs with an electric propulsion system. The MTOW of such vehicles is largely determined by the batteries’ weight, which in turn is directly determined by the lift-to-drag ratio, strongly dependent on the aspect ratio and leading-edge sweep angle, while the considered parameters have no significant impact on the design weight of small UAVs, unlike the manufacturing technology and the absolute dimensions of the wing structure.

In the second iteration, a rational combination of wing loading and cruise speed at “freezing” parameters of AR = 4 and Λ = 17 are selected. Figure 9 shows the obtained response surfaces.

The response surfaces of the objective function are shown in Figure 9a,b, and the region of the feasible solution is represented in color. The line along which the surface breaks define the domain of the sizing equation. For the given input data, the best combination for minimization of W₀ = 1.568 kg was (W/S) = 8.7 daN/kg and v = 20 m/s, and for maximization of ^L/_D = 19.97 was ^W/_S = 4.6 daN/kg and v = 20 m/s. The difference of optimal parameter values in the optimization of different objective functions can be explained by the fact that the wing loading determines the wing area and significantly affects the structure weight; despite the need to increase the power unit and batteries weight when increasing the wing loading, reducing the structure weight leads to a decrease in takeoff weight. At the same time, the maximum lift-to-drag ratio is realized at smaller angles of attack and requires a lower flight speed and lower wing loading.

The validation of the SHADE E-PSR algorithm was assessed based on the repeatability of the results obtained. The optimization parameters of the SHADE E-PSL are presented in

Table 5. Optimization parameters.

Optimization Parameters		Value
Initial population, vector		60
Maximum number of objective function evaluations		6000
Minimal final population size		6
Threshold value ε, kg		0.01
SHADE algorithm parameters	H	6
	P	0.11
	rA	2.6
Initial mutation operator, Fi		0.5
Initial crossover probability of the design variable vector CRi		0.5

.

The algorithm was executed ten times with different initial populations. To ensure the randomness of the design variable vectors, each initial sample was generated with the Latin hypercube sampling method [60] from the SMT (surrogate modelling toolbox) package [61].

Table 6. Statistical measures of the optimal vector of each SHADE E-PSR algorithm run.

	Max	Min	Median	x, kg	σ, kg	CV, %
L(x)	2.234	2.211	2.222	2.223	0.007	0.31

presents the results of the validation of the algorithm; the taken sample consists of ten vectors, each vector corresponding to the best of the optimal remaining vector after each algorithm run.

Analysis of the results in Table 6 confirms the good performance of the algorithm due to the variation coefficient value of 0.31%.

In addition, a statistical analysis of the design variables was performed to investigate the tendency of the differential evolution algorithm to find the global minimum. The taken sample consists of 60 individuals fulfilling at least one of the algorithms’ stopping criteria.

Table 7. Statistical measures of the design variables and the objective function of the optimal vectors.

	Design Variables						Objective Function
	AR	Λ, °	λ	θ, °	W/S, daN/kg	v, m/s	W0, kg
x	5.08	23.16	1.01	−2.64	4.73	14.68	2.229
σ	0.33	3.34	0.02	1.74	0.20	0.33	0.007
CV, %	6%	14%	2%	−66%	4%	2%	0.32%

presents the statistical indicators of the optimization results.

4. Cases of Study

The presented method for conceptually designing electric flying wing aircraft was tested by solving three case studies. First, by modernizing an existing flying wing UAV. Second, by analyzing the effect of different payloads and endurance on the MTOW. Third, by analyzing different static margins on the aircraft performance characteristics.

4.1. Modernization of Existing UAV

The UAV to be modernized is a UAV “Boomerang”, designed according to the flying wing configuration with a twin-wing vertical tail, and a single-engine propulsion system consisting of a brushless motor. A layout is shown in Figure 10.

The geometric, flight performance, weight, mass, and aerodynamic characteristics of the UAV “Boomerang” are presented in

Table 8. UAV specifications.

	UAV A “Boomerang”	UAV B	UAV C
Geometric
AR	3.3	5.4	4.7
Λ, °	11.3	24.6	17.9
λ	1.3	1.0	1.0
θ, °	−2.6	−2.5	−3.2
ψ, °	−0.5	0	0
b, m	1	1.043	0.988
S, m2	0.3	0.203	0.206
cr, m	0.345	0.194	0.208
ct, m	0.245	0.194	0.208
MAC, m	0.297	0.194	0.208
Flight-performance
t, hr (min)	0.66 (40)	0.66 (40)	0.66 (40)
W/S, daN/m2	7.5	10.1	9.9
V, m/s	20	21.51	21.27
$\left(\frac{\mathrm{P}}{\mathrm{W}}\right)$, kW/kg	0.241	0.259	0.256
Weight and mass
W0, kg	2.265	2.046	2.039
Wpayload $\left(\frac{{\mathrm{W}}_{\mathrm{payload}}}{{\mathrm{W}}_0}\right)$, kg	0.500 (0.221)	0.500	0.500
Wstruct $\left(\frac{{\mathrm{W}}_{\mathrm{struct}}}{{\mathrm{W}}_0}\right)$, kg	0.589 (0.260)	0.398	0.402
Wbatt $\left(\frac{{\mathrm{W}}_{\mathrm{batt}}}{{\mathrm{W}}_0}\right)$, kg	0.631 (0.279)	0.603	0.595
Wpu $\left(\frac{{\mathrm{W}}_{\mathrm{pu}}}{{\mathrm{W}}_0}\right)$, kg	0.175 (0.077)	0.175	0.172
Wequip $\left(\frac{{\mathrm{W}}_{\mathrm{equip}}}{{\mathrm{W}}_0}\right)$, kg	0.300 (0.132)	0.300	0.300
Wprop $\left(\frac{{\mathrm{W}}_{\mathrm{prop}}}{{\mathrm{W}}_0}\right)$, kg	0.020 (0.009)	0.020	0.020
Wreserve $\left(\frac{{\mathrm{W}}_{\mathrm{reserve}}}{{\mathrm{W}}_0}\right)$, kg	0.050 (0.022)	0.050	0.050
${\overline{x}}_{CG}$	0.083	0.136	0.099
kMGW	4.52	4.09	4.08
Aerodynamic
CL cruise	0.32	0.35	0.35
CD cruise	0.017885	0.018187	0.018274
${\left(\frac{\mathrm{L}}{\mathrm{D}}\right)}_{\mathrm{cruise}}$	17.91	19.30	19.29
α, °	7.2	7.4	8.1
${\overline{\mathrm{l}}}_{\mathrm{el}}$	0.736	1.075	0.947

. Table 3 presents the input data of the optimization algorithm for calculating the objective function. A couple of changes were introduced to match the characteristics of the “Boomerang”; the mass of the equipment is duplicated, and the flight endurance was changed from 1 h to 40 min. Table 4 presents the intervals of the design variables for UAV parameter optimization. The value of the taper ratio was fixed to 1 due to the almost null correlation with either the objective function or the constraints. Table 5 presents the parameters of the SHADE E-PSR evolutionary algorithm for UAV parameter optimization.

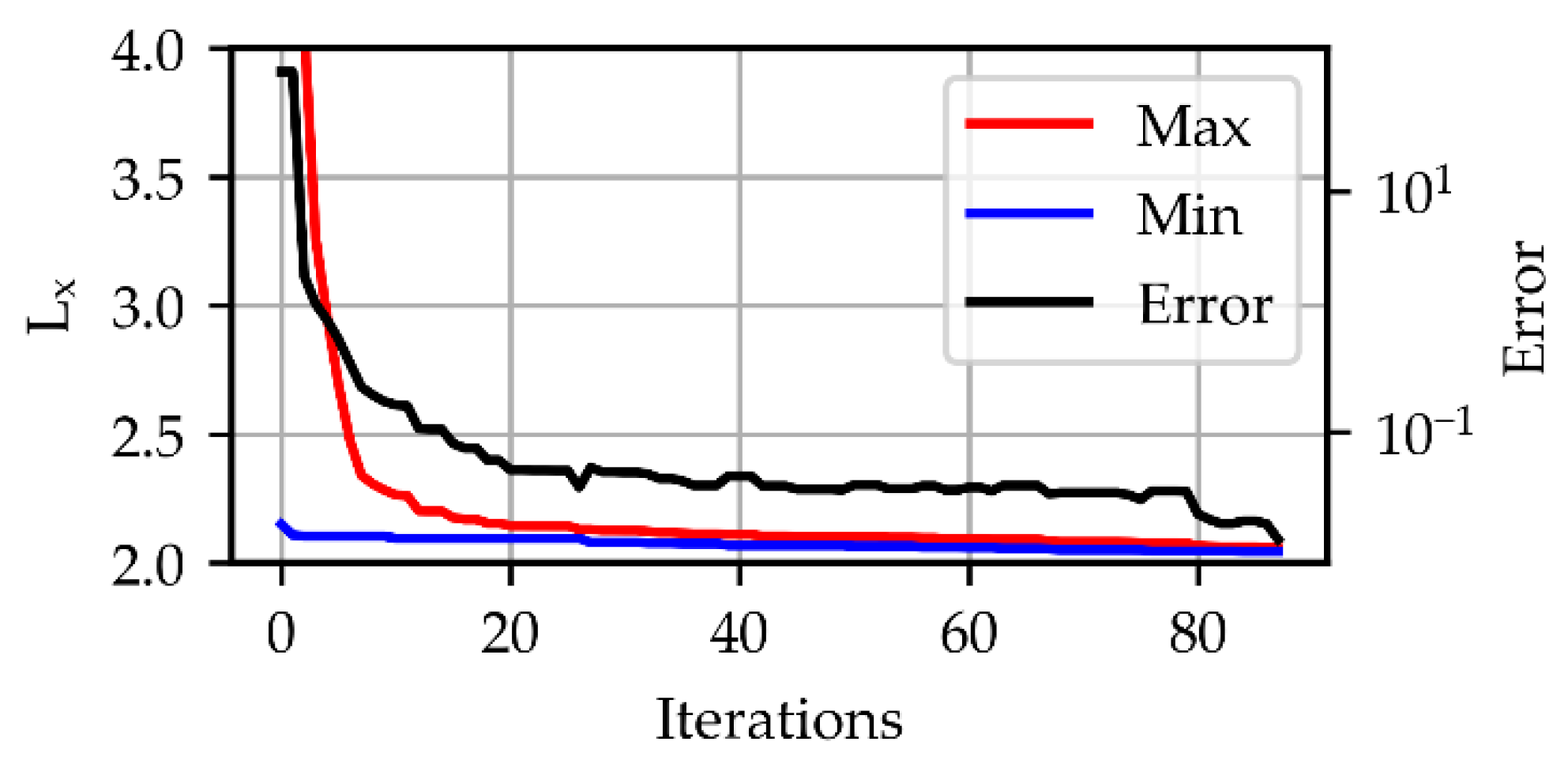
The initial population size consists of 60 vectors, in each generation the algorithm reduces the population based on the upper limit of MTOW. Figure 11 shows the evolution of the population over the iterations, and the maximum and minimum values of the penalty function at each iteration.

In this study, convergence was achieved after 88 iterations. The design variables corresponding to the optimal vector and their corresponding objective and constraint function values are shown in Table 8. The layout of the resulting optimum UAVs and the UAV subjected to modification are shown in Figure 12.

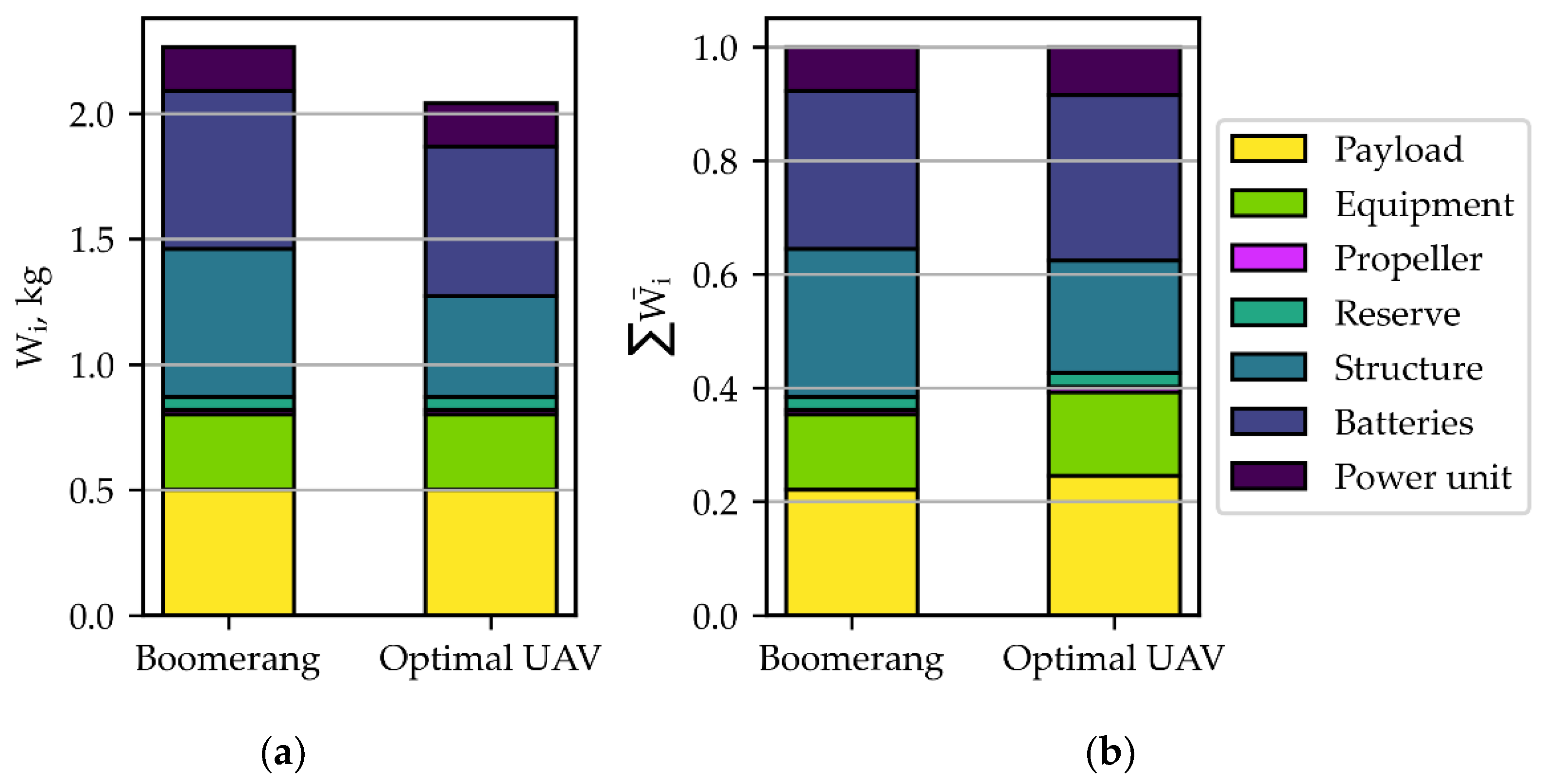
Notably, as a result of the optimization, we obtained a UAV (Figure 12b,c) of smaller area compared with the original (Figure 12a), which can be explained not only by an increase in the wing loading as a consequence of the reduction in the wing structure weight due to the reduction of its area but also by a reduction in the aircraft weight due to the batteries weight reduction, due to the lowering of the specific energy consumption. Despite some increase in flight speed, the decrease in power consumption was achieved due to an increase in the lift-to-drag ratio caused by an increase in the wing aspect ratio and the cruise flight execution at more optimal angles of attack. The reduction in wing structure weight by 32% led to an improvement in the objective function by about 9.8%. This example also clearly demonstrates the effect of the minimum elevon arm constraint in the longitudinal axis on the optimization result: increasing the wing aspect ratio to improve the lift-to-drag ratio also requires increasing the leading-edge sweep angle of the wing to ensure pitch control. The effect of the constraint is clearly visible in the two competing variants B and C, and it is noticeable that these modifications do not differ much in terms of weight summary. The improvement in take-off weight for the “B” and “C” aircraft relative to the “A” aircraft is shown in Figure 13. Figure 12 illustrates the change in the appearance of the aircraft top view for the variants considered. Moreover, the efficacy of the resulting wings by optimization was demonstrated by comparing the aircraft gross weight factor of the initial and optimized wings; the value of k_MGW was reduced by 10.7%.

4.2. Effect of Change in Payload and Endurance on MTOW

For the second and third cases of study, the same input data were used, as presented in Table 3. The weight of the propeller is considered part of the reserve weight.

Figure 14 shows the weight summary for several payload weights. The ratios of change of different payloads to the MTOW and variable weights are presented in

Table 9. Component weight ratio with respect to the change in payload weight.

Component	ΔWi/ΔWpayload	ΔWi/ΔW0	kMGW
Payload	1	0.3951	2.5312
Structure	0.4416	0.1913	5.2274
Batteries	0.8570	0.3386	2.9533
Power unit	0.1675	0.0632	15.8228
MTOW	2.5312	1	1

. It is observed that the change in the payload weight generates a linear increment in the variable weights. This is confirmed in Figure 14, in which the dependence of different weight components on the payload is more intuitive. Moreover, the battery weight increases at almost twice the increment of the structure weight.

The mass growth factor and its effects are presented in

Table 10. MTOW dependence on the change in payload weight.

Payload, kg	kMGW	Effect on Additional kMGW, %	W0, kg	Effect on Original Additional Weight, %
0.5	3.55		1.773
1	2.97	−16%	2.969	67%
1.5	2.73	−23%	4.098	131%
2	2.68	−25%	5.351	202%
2.5	2.58	−27%	6.456	264%
3	2.56	−28%	7.667	332%

. If the payload weight is changed by 100%, the mass growth factor changes by −23%. For a 200% conversion, it is −27%. Table 10 and Figure 14 clearly outline the cause of the problem for large electric aircraft: as the payload weight increases, the payload weight efficiency rapidly deteriorates, while the rest of the conditions remain equal, and it is possible to find the minimum value of the mass growth factor of the given design task.

For the study of the effect of the endurance on the MTOW, the endurance of 1 hr was increased and the change of the mass growth factor was recorded. The results are summarized in Table 10. Figure 15 shows the weight summary for several endurances. It is observed that the change in the endurance generates a linear increment in the variable weights, as in the previous scenario, except for the structure weight, which falls to the lower interval of the wing loading during the optimization process.

Table 11. MTOW dependence on the change in endurance.

Endurance, h	kMGW	Effect on Additional kMGW, %	W0, kg	Effect on Original Additional Weight, %
1	3.55		1.773
1.5	5.26	48%	2.628	48%
2	6.89	94%	3.443	94%
2.5	11.06	212%	5.531	212%
3	19.41	447%	9.704	447%

presents the effect of the endurance change on the MTOW. It was noticed that if the endurance is changed by 50%, the mass growth factor changes by 48%. If the range grows by 100%, the factor grows by 94%. This sensitivity is highly dependent on the initial endurance at the maximum fixed weight. In the right column, the effect is shown on the original additional weight. The more endurance grows, the greater the mass growth factor is. The more the UAV endures, it carries more batteries, which increases its fraction; hence, the mass growth factor is correspondingly high. The greater the sum of the variable weight fractions approaches 1, the more the mass growth factor will grow.

By comparing the effect of the change of the payload weight and the change of the endurance on the MTOW, it is observed that the endurance is more sensitive than when increasing the payload. Indeed, the MTOW dependence on endurance is non-linear.

4.3. Effect of Different Static Margins on the Aerodynamic Characteristics

Figure 16 shows the main and standard deviations of the angle of attack and the lift-to-drag ratio. The results of the third case of study show that the angle of attack is highly dependent on the static margin. The angle of attack shows little deviation compared to the lift-to-drag ratio, mainly at margins 0 and 0.5.

An increase in static stability leads to an increase in pitch movement. Trimming the UAV, in this case, is ensured by deflecting the elevons upward, or by using airfoils with a more upward leading-edge angle. The lift coefficient required for the horizontal flight can be maintained by increasing the angle of attack (Figure 16a). The flying wing trim at different angles of attack due to changes in the static stability causes changes in the lift-to-drag ratio. By shifting the center of gravity, the static margin, it is possible to trim the aircraft at the most favorable angles of attack with the maximum lift-to-drag ratio. However, for each degree of the static longitudinal static margin, a choice of optimal parameters was made; for example, for low static margins, it was required to increase the wing loading and, in contrast, increasing the static margin led to the need to reduce the wing loading to change the angles of attack to a more optimal configuration. Therefore, in the range considered, the degree of the aircraft static margin did not significantly affect the lift-to-drag ratio.

5. Discussion

First, this work presented an MDAO method and two optimization processes for minimizing the MTOW of a flying wing UAV during the conceptual design step by choosing the optimal geometrical and flight conditions. The Gauss-Seidel method and response surface method for a couple of parameters were used to verify the correctness of the obtained results, and to visualize the solution during the differential evolutionary algorithm testing, which also allowed us to trace the correctness of applying restrictions. Similarly, using the response surface method, both the graphical solution of UAV trimming and the solution to the COBYLA algorithm were attained, which were used within the developed MDAO method. The optimization process, based on a differential evolution algorithm and penalty functions, allowed for the generation of not just one, but several design solutions (depending on the minimum threshold specified within the solver) which converged to the same MTOW value with a coefficient of variation of 0.31%. This means that it is highly probable, with the application of the second algorithm, to find the global minimum of the design task. In both optimization processes, the UAV was trimmed by solving an optimization routine within the main optimization process. The twist angle had demonstrated to have a slight influence on the MTOW. It was found that the aspect ratio and the leading-edge sweep angle are highly correlated (not a surprise given that both are linked through the maneuverability constraint) making it possible to reduce the number of design variables, by making one dependent on the other, in future works.

Second, results on the modernization of an existing UAV showed that, with the application of this method, it is possible to optimize the conceptual design; in our study, by a 22% improvement. Results concerning the investigation on the effect of different payloads and endurance on the MTOW showed that by incrementing the payload weight, the mass growth factor decreases, converging to 2.5; this is an indication that by incrementing the payload up to the value corresponding to the mass growth factor, the UAV becomes more efficient. However, by increasing the payload, the MTOW increases to a point (that depends on the structural material), in which the structure weight calculation must account for the stresses. The MTOW dependence on endurance is non-linear, and, by looking at the divergence of the mass growth factor, we observed that by incrementing the endurance, the task becomes unsolvable. When the sum of the weight ratios is more than 1, the computed value lies outside the sizing equation domain. These studies are valid for mass increasing close to the center of gravity; if the mass increment happens, for instance, at the nose of the UAV, the results are expected to be different. This tells us that the work could be further improved by adding a weight distribution model that could not only more precisely calculate the aircraft weight factor when the weight increment is far from the center of gravity, but also account for a more accurate interaction between stability and weight disciplines.

And finally, the results of the investigation on the effect of different static margins on the aerodynamic characteristics showed that one of the main benefits of choosing a less stable, even a neutral or unstable configuration, would be that trimming the UAV is possible at a lower angle of attack; especially important with a flying wing configuration. However, a negative impact could be that the uncertainty regarding lift-to-drag ratio is higher.

Future works on this topic will be aimed toward extending this technique to other aerodynamic schemes of UAVs, introducing into the algorithm the requirements of lateral stability and control, and adding a weight distribution model that could not only more precisely calculate the aircraft weight factor when the weight increment is far from the center of gravity, but also account for a more accurate interaction between stability and weight disciplines.

6. Conclusions

The developed MDAO method for conceptually designing electric flying-wing UAVs makes it possible to obtain a sufficiently detailed view of the designed aircraft, including its optimal geometric, flight parameters, as well as the corresponding flight performance and weight summary of the components at a sufficiently low computational and time costs. Several used constraints allow us to obtain the optimal solution, consider aircraft trimming with a given static margin, and consider the requirements of pitch control. The method was verified by performing a mesh independence study, comparing optimization solutions for the trimming of the UAV against geometrical solutions, assessing the SHADE E-PSR algorithm, and evaluating the deviation of the objective function.

The introduction of the MTOW as a parameter within the differential evolutionary algorithm and the consequent reduction of its upper interval value by taking the maximum MTOW, in the previous iteration, made it possible to dispense of an extra internal cycle for solving the sizing equation at each optimization step; therefore, increasing the algorithm performance. Another advantage of using this method in design is the possibility to obtain not just one optimal solution, but a few concurrent options due to a low coefficient of variance; the values of the design variables can significantly vary, indicating the possible presence of several minima towards the global minima. The application of traditional optimization methods would lead to only one of the minima, ignoring the others.

The application of this method in UAV conceptual design will make it possible to quickly study the impact of changes in various parameters and flight conditions on flight performance, and technical and economic indicators, which are relevant in the design of new vehicles, and in the modernization of existing ones. Typical examples of solving such design problems have been considered in the work.