Joint Placement and Power Optimization of UAV-Relay in NOMA Enabled Maritime IoT System
Abstract
1. Introduction
1.1. Recent Works
1.2. Motivation and Contributions
- In this paper, we study the power minimization problem subject to user’s minimum rate requirement and UAV transmit power budget in a maritime IoT system with A2A and A2S link model considered. A coordinated direct and relay transmission scheme employing uplink NOMA scheme is proposed and investigated, where maritime close-shore users (MCU) directly communication with onshore BS, whereas maritime remote users (MRU) communicate with the onshore BS by a half-duplex DF UAV relay.
- In the proposed maritime IoT system, an interference cancellation parameter is introduced to summarized UAV’s received data expression in transmission phase 1, which facilitates solving the proposed UAV power transmission minimization problem.
- The successive convex approximation method is applied to deal with non-convex inequality constraints of the formulated optimization problem. The block coordinate descent method (BCD) is used to decouple the original problem into two subproblems, namely power allocation and optimal UAV placement. After that, an iterative algorithm is proposed to optimize power allocation coefficients and optimal UAV coordinates alternately.
1.3. Paper Organization
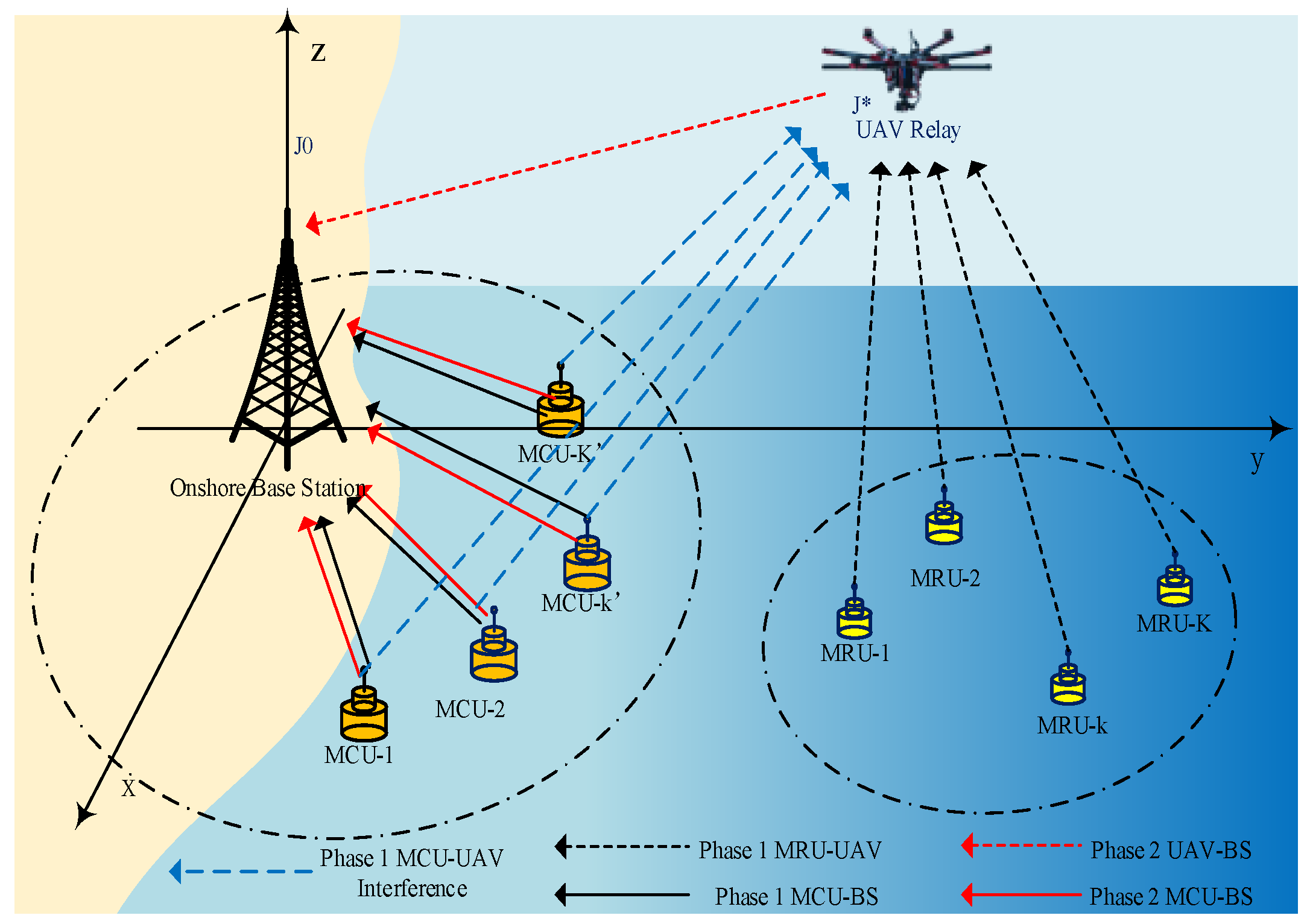
2. System Model and Problem Formulation
2.1. System Model
- 1.
- Phase-1 ()In an uplink NOMA transmission scenario, an MCU and an MRU transmit symbols and simultaneously with and , where denotes the total transmit power in phase 1. and are the power allocation coefficient in phase 1. To guarantee an efficient SIC decoding at the NOMA receiver, it is assumed that . Thus, data received at onshore BS and the UAV in Phase 1 can be given, respectively, by:where denotes the background noise. Due to the half-duplex relay scheme, the achievable rate of the -th MCU at BS in phase 1 can be represented as:where . Because of the simultaneous transmission of MRU and MCU, UAV is able to receive the signal from both of them. We assume perfect time synchronization between MRU and MCU. According to the uplink NOMA principle, the UAV relay obtains the decoded symbol by considering the following two conditions.By introducing as the interference cancellation parameter, the received data rate at UAV in Phase 1 can be summarized as:
- 2.
- Phase-2 ()In phase 2, both MCU and UAV transmit symbols and simultaneously to onshore BS with powers and , where , are the power allocation coefficient in phase 2 and . Thus, received data at onshore BS can be represented as:Since , the achievable data rates of the UAV relay and MCU are presented, respectively, by:
- 3.
- Sum Capacity
2.2. Problem Formulation
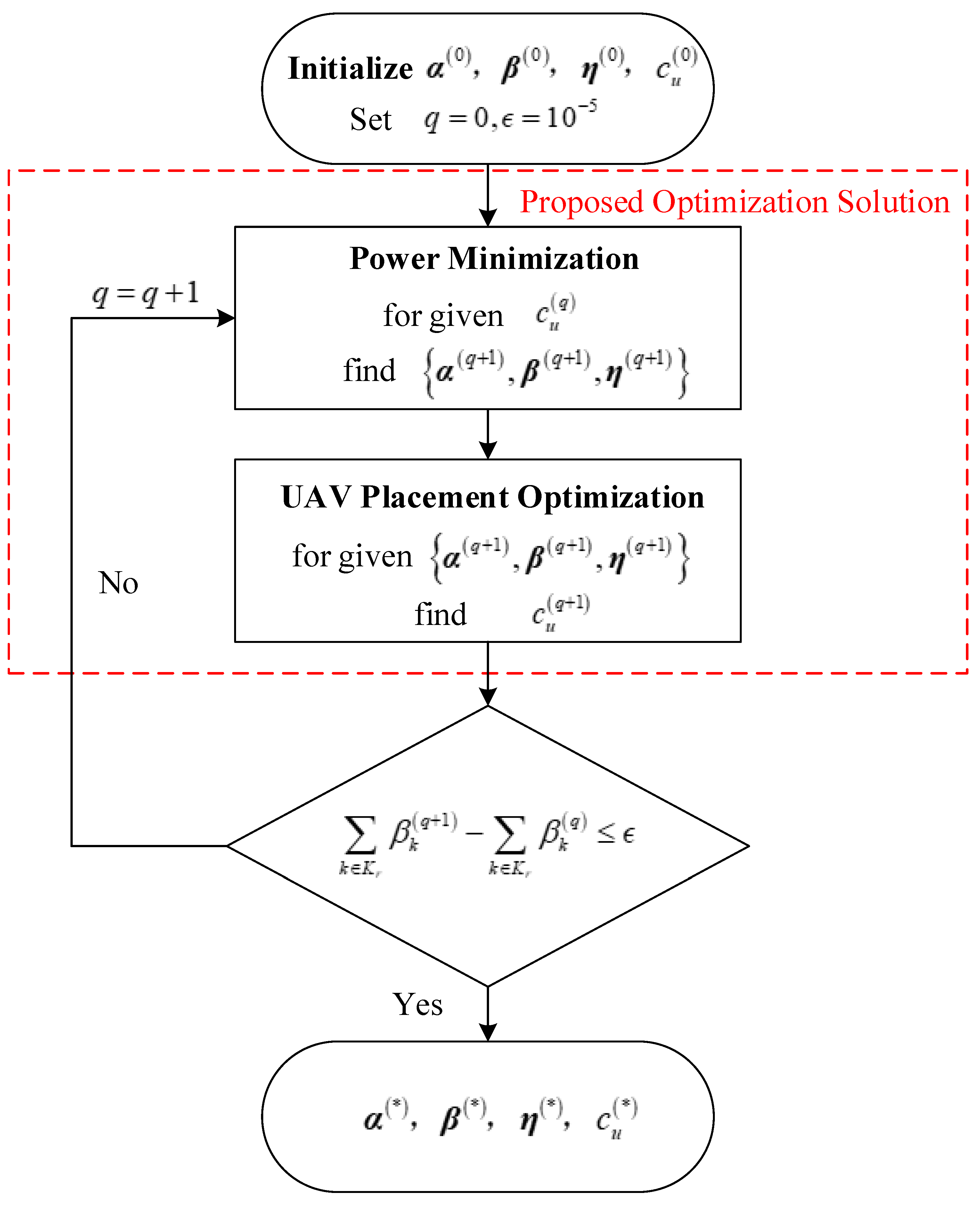
3. Proposed Optimization Solution
3.1. Power Minimization
3.2. UAV Placement Optimization
3.3. Iterative Algorithm
| Algorithm 1 BCD Method for Joint Placement and Power Optimization |
|
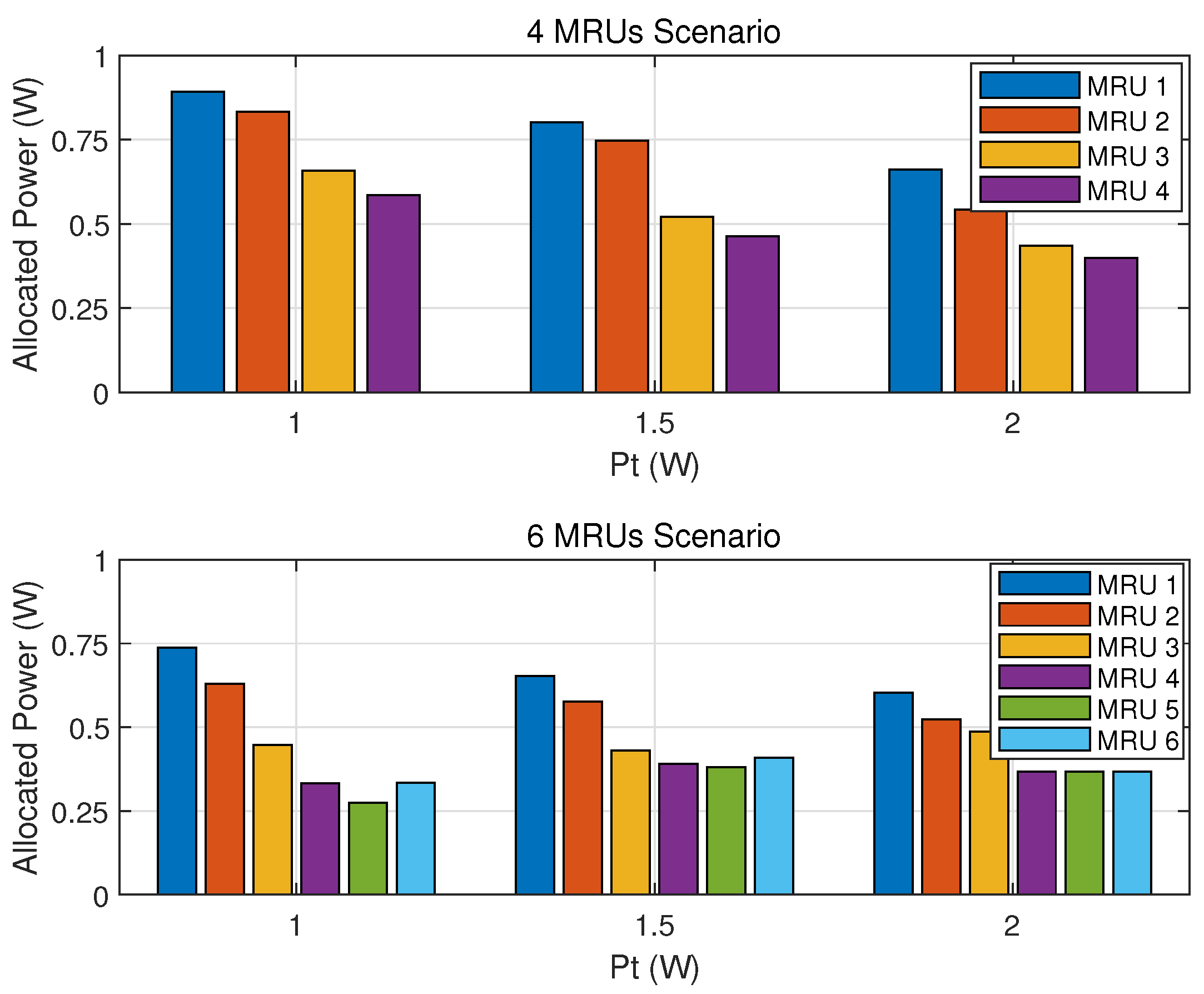
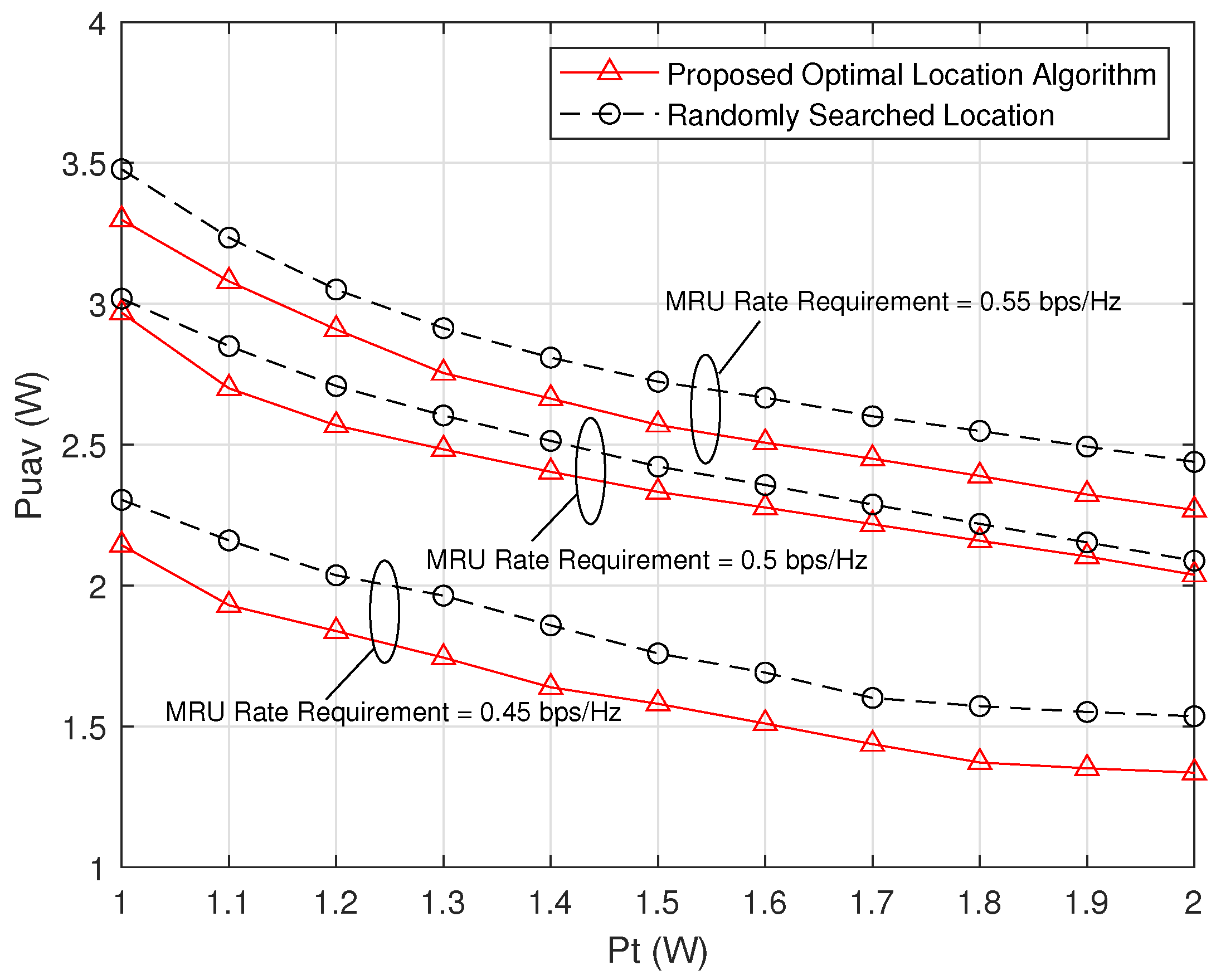
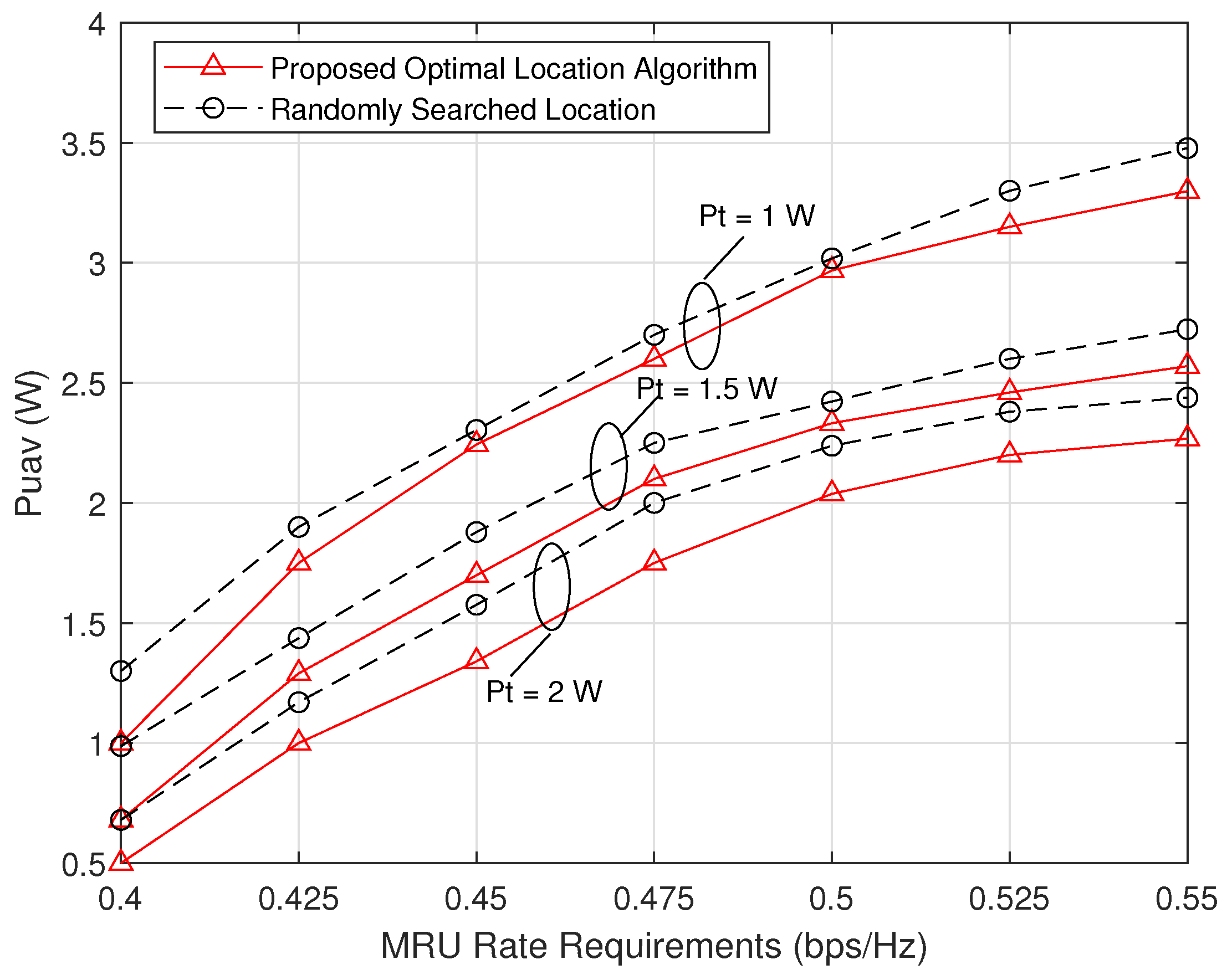
4. Numerical Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, X.; Feng, W.; Wang, J.; Chen, Y.; Ge, N.; Wang, C.X. Enabling 5G on the ocean: A hybrid satellite-UAV-terrestrial network solution. IEEE Wirel. Commun. 2020, 27, 116–121. [Google Scholar] [CrossRef]
- Lopes, M.J.; Teixeira, F.; Mamede, J.B.; Campos, R. Wi-Fi broadband maritime communications using 5.8 GHz band. In Proceedings of the Underwater Communications Networking, Levante, Italy, 3–5 September 2014. [Google Scholar]
- Teixeira, F.B.; Campos, R.; Ricardo, M. Height optimization in aerial networks for enhanced broadband communications at sea. IEEE Access 2020, 8, 28311–28323. [Google Scholar] [CrossRef]
- Ji, X.; Wang, J.; Li, Y.; Sun, Q.; Xu, C. Modulation recognition in maritime multipath channels: A blind equalization-aided deep learning approach. China Commun. 2020, 17, 12–25. [Google Scholar] [CrossRef]
- Wei, T.; Feng, W.; Chen, Y.; Wang, C.X.; Ge, N.; Lu, J. Hybrid satellite-terrestrial communication networks for the maritime internet of things: Key technologies, opportunities, and challenges. IEEE Internet Things J. 2021, 8, 8910–8934. [Google Scholar] [CrossRef]
- Wang, N.; Li, F.; Chen, D.; Liu, L.; Bao, Z. NOMA-based energy-efficiency optimization for UAV enabled space-air-ground intergarted relay networks. IEEE Trans. Veh. Technol. 2022, 71, 4129–4141. [Google Scholar] [CrossRef]
- Liu, C.; Feng, W.; Chen, Y.; Wang, C.X.; Ge, N. Cell-Free Satellite-UAV Networks for 6G Wide-Area Internet of Things. IEEE J. Sel. Areas Commun. 2021, 39, 1116–1131. [Google Scholar] [CrossRef]
- Liu, X.; Wang, J.; Zhao, N.; Chen, Y.; Zhang, S.; Ding, Z.; Yu, F.R. Placement and power allocation for NOMA-UAV networks. IEEE Wirel. Commun. Lett. 2019, 8, 965–968. [Google Scholar] [CrossRef]
- Sharma, P.K.; Kim, D.I. UAV-enabled downlink wireless system with non-orthogonal multiple access. In Proceedings of the 2017 IEEE Globecom Workshops (GC Wkshps), Singapore, 4–8 December 2017. [Google Scholar]
- Sohail, M.F.; Leow, C.Y.; Won, S. Non-orthogonal multiple access for unmanned aerial vehicle assisted communication. IEEE Access 2018, 6, 22716–22727. [Google Scholar] [CrossRef]
- Nasir, A.A.; Tuan, H.D.; Duong, T.Q.; Poor, H.V. UAV-enabled communication using NOMA. IEEE Trans. Commun. 2019, 67, 5126–5138. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, H.; Li, Y.; Sun, Q.; Wu, Y.; Jin, S.; Quek, T.Q.S.; Xu, C. Wireless channel models for maritime communications. IEEE Access 2018, 6, 68070–68088. [Google Scholar] [CrossRef]
- Zhang, J.; Liang, F.; Li, B.; Yang, Z.; Wu, Y.; Zhu, H. Placement optimization of caching mobile relay maritime communication. China Commun. 2020, 17, 209–219. [Google Scholar] [CrossRef]
- Tang, R.; Feng, W.; Chen, Y.; Ge, N. NOMA-based UAV communications for maritime coverage enhancement. China Commun. 2021, 18, 230–243. [Google Scholar] [CrossRef]
- Li, X.; Feng, W.; Chen, Y.; Wang, C.X.; Ge, N. Maritime coverage enhancement using UAVs coordinated with hybrid satellite-terrestrial networks. IEEE Trans. Commun. 2020, 68, 2355–2369. [Google Scholar] [CrossRef]
- Ma, R.; Wang, R.; Liu, G.; Chen, H.H.; Qin, Z. UAV-assisted data collection for ocean monitoring networks. IEEE Netw. 2020, 34, 250–258. [Google Scholar] [CrossRef]
- Lyu, L.; Chu, Z.; Lin, B.; Dai, Y.; Cheng, N. Fast trajectory planning for UAV-enabled maritime IoT systems: A Fermat-Point based approach. IEEE Wirel. Commun. Lett. 2022, 11, 328–332. [Google Scholar] [CrossRef]
- Jiang, X.; Wu, Z.; Yin, Z.; Yang, Z.; Zhao, N. Power comsumption minimization of UAV relay in NOMA networks. IEEE Wirel. Commun. Lett. 2020, 9, 666–670. [Google Scholar] [CrossRef]
- Guo, Y.; Yin, S.; Hao, J. Joint placement and resource optimization for multi-user UAV-relaying system with underlaid cellular networks. IEEE Trans. Veh. 2020, 10, 12374–12377. [Google Scholar] [CrossRef]
- Wang, D.; Zhou, F.; Lin, W.; Ding, Z.; Al-Dhahir, N. Cooperative Hybrid Non-Orthogonal Multiple Access Based Mobile-Edge Computing in Cognitive Radio Networks. IEEE Trans. Cogn. Commun. Netw. 2022, 8, 1104–1117. [Google Scholar] [CrossRef]
- Wang, D.; He, T.; Zhou, F.; Cheng, J.; Zhang, R.; Wu, Q. Outage-driven link selection for secure buffer-aided networks. Sci. China Inf. Sci. 2022, 65, 182303. [Google Scholar] [CrossRef]
- Matolak, D.W.; Sun, R. Air-ground channel characterization for unmanned aircraft systems—Part I: Methods, measurements, and models for over-water settingse. IEEE Trans. Veh. Technol. 2017, 66, 26–44. [Google Scholar] [CrossRef]
- Wu, S.; Wang, C.X.; Alwakeel, M.M.; You, X. A general 3-D non-stationary 5G wireless channel model. IEEE Trans. Commun. 2018, 66, 3065–3078. [Google Scholar] [CrossRef]
- Zeng, L.; Cheng, X.; Wang, C.X.; Yin, X. Second order statistics of non-isotropic UAV Ricean fading channels. In Proceedings of the IEEE 86th Vehicle Technology Conference (VTC-Fall), Toronto, ON, Canada, 24–27 September 2017. [Google Scholar]
- Kang, Z.; You, C.; Zhang, R. 3D Placement for Multi-UAV Relaying: An Iterative Gibbs-Sampling and Block Coordinate Descent Optimization Approach. IEEE Trans. Commun. 2021, 69, 2047–2062. [Google Scholar] [CrossRef]
- Wang, D.; Wu, M.; He, Y.; Pang, L.; Xu, Q.; Zhang, R. An HAP and UAVs Collaboration Framework for Uplink Secure Rate Maximization in NOMA-Enabled IoT Networks. Remote. Sens. 2022, 14, 4501. [Google Scholar] [CrossRef]
- Huang, W.; Yang, Z.; Pan, C.; Pei, L.; Chen, M.; Shikh-Bahaei, M.; Elkashlan, M.; Nallanathan, A. Joint power, altitude, location and bandwidth optimization for UAV with underlaid D2D communications. IEEE Wirel. Commun. Lett. 2019, 8, 524–527. [Google Scholar] [CrossRef]

| Parameter | Description | Value |
|---|---|---|
| Coordination of onshore BS | ||
| Flight altitude of UAV | 150 m | |
| Reference distance | 1 m | |
| Carrier frequency | 5 MHz | |
| Background noise | dBm | |
| c | Light speed | m/s |
| UAV transmit power budget | 4 W | |
| A2S link path loss at | 116.7 | |
| A2S link path loss exponent | 20 | |
| standard deviation of | 0.1 | |
| A2S link Rician factor | 30 | |
| A2A linkpath loss at | 46.4 | |
| A2A link path loss exponent | 15 | |
| standard deviation of | 0.1 | |
| A2A link Rician factor | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Tian, J.; Gu, L.; Tao, S. Joint Placement and Power Optimization of UAV-Relay in NOMA Enabled Maritime IoT System. Drones 2022, 6, 304. https://doi.org/10.3390/drones6100304
Xu W, Tian J, Gu L, Tao S. Joint Placement and Power Optimization of UAV-Relay in NOMA Enabled Maritime IoT System. Drones. 2022; 6(10):304. https://doi.org/10.3390/drones6100304
Chicago/Turabian StyleXu, Woping, Junhui Tian, Li Gu, and Shaohua Tao. 2022. "Joint Placement and Power Optimization of UAV-Relay in NOMA Enabled Maritime IoT System" Drones 6, no. 10: 304. https://doi.org/10.3390/drones6100304
APA StyleXu, W., Tian, J., Gu, L., & Tao, S. (2022). Joint Placement and Power Optimization of UAV-Relay in NOMA Enabled Maritime IoT System. Drones, 6(10), 304. https://doi.org/10.3390/drones6100304






