Abstract
Deriving crop information from remotely sensed data is an important strategy for precision agriculture. Small unmanned aerial systems (UAS) have emerged in recent years as a versatile remote sensing tool that can provide precisely-timed, fine-grained data for informing management responses to intra-field crop variability (e.g., nutrient status and pest damage). UAS sensors with high spectral resolution used to compute informative vegetation indices, however, are practically limited by high cost and data dimensionality. This research extends spectral analysis for remote crop monitoring to investigate the relationship between crop health and 3D canopy structure using low-cost UAS equipped with consumer-grade RGB cameras. We used flue-cured tobacco as a case study due to its known sensitivity to fertility variation and nutrient-specific symptomology. Fertilizer treatments were applied to induce plant health variability in a 0.5 ha field of flue-cured tobacco. Multi-view stereo images from three UAS surveys collected during crop development were processed into orthoimages used to compute a visible band spectral index and photogrammetric point clouds using Structure from Motion (SfM). Plant structural metrics were then computed from detailed high resolution canopy surface models (0.05 m resolution) interpolated from the photogrammetric point clouds. The UAS surveys were complimented by nutrient status measurements obtained from plant tissues. The relationships between foliar nitrogen (N), phosphorus (P), potassium (K), and boron (B) concentrations and the UAS-derived metrics were assessed using multiple linear regression. Symptoms of N and K deficiencies were well captured and differentiated by the structural metrics. The strongest relationship observed was between canopy shape and N foliar concentration (adj. = 0.59, increasing to adj. = 0.81 when combined with the spectral index). B foliar concentration was consistently better predicted by canopy structure with a maximum adj. = 0.41 observed at the latest growth stage surveyed. Overall, combining information about canopy structure and spectral reflectance increased model fit for all measured nutrients compared to spectral alone. These results suggest that an important relationship exists between relative canopy shape and crop health that can be leveraged to improve the usefulness of low cost UAS for precision agriculture.
1. Introduction
One of the primary goals of precision agriculture is identifying intra-field variability to enable a management response to plant stress that will maximize yield. Currently, farmers monitor crop health in high-value crops through labor-intensive scouting, destructive field sampling, and costly laboratory assays. Remote sensing, however, is increasingly being used as an alternative tool for crop monitoring that more accurately accounts for spatial variations in crop stress across a field [1]. Small unmanned aerial systems (UAS) have emerged in recent years as a versatile remote sensing tool used by scientists and agricultural producers for collecting data at very high spatial and temporal resolutions [2,3]. UAS can provide precisely-timed, fine-grained data for informing spatially variable management responses for maximizing crop productivity while minimizing natural resource degradation.
One of the most promising application of remote sensing in agriculture is identifying symptoms from biotic and abiotic plant stressors, such as nutrient deficiencies, pest pressure, and harsh environmental conditions. In particular, monitoring plant nutrition with remote sensing has been successfully demonstrated by numerous studies [4,5,6,7]. Symptoms of deficiencies of essential macronutrients, like nitrogen (N), phosphorus (P), and potassium (K), can often be differentiated visually, making remote identification possible. These nutrients perform crucial roles in plant development and are needed in relatively high concentrations at specific plant growth stages [8]. Nutrient toxicity is also important to monitor for many crops, such as boron (B) in flue-cured tobacco, which has negative effects on leaf quality due to increased nicotine and other alkaloids [9,10,11]. Remote monitoring of crop nutrient status with UAS can provide on-demand, fine-grained spatial information to improve crop productivity and minimize over-application of fertilizers if integrated into existing precision agriculture technology used on-board commercial tractors and implements.
Nutrient deficiencies often cause visible changes in foliar coloration, appearing yellow (chlorotic), white (bleached), brown (necrotic), red, or black [12]. These well-documented deficiencies can be measured by sensors as changes in spectral reflectance and enable noninvasive diagnostics of plant nutrient disorders. Vegetation indices, like Normalized Difference Vegetation Index (NDVI), measured by broadband multispectral sensors have been shown to strongly correlate with crop health and are widely used in agriculture and throughout the literature [13,14,15,16]. Hyperspectral sensors with very fine spectral resolution also have the potential to measure unique spectral signatures for nutrient disorders [7,17,18]. However, practical application of UAS hyperspectral imagery to diagnose nutrient disorders in production agriculture remains limited by high costs, high data dimensionality, and the need for advanced data analysis skills. UAS with optical cameras, in contrast, are inexpensive and often supported by cloud-based data storage and processing, making them easier to use by farmers without remote sensing data processing skills [2]. Optical cameras provide visible band imagery that can be used to calculate vegetation indices, like Visible Atmospheric Resistant Index (VARI) and Triangular Greenness Index (TGI) [19]. These RGB indices have been shown to correlate well with leaf area index and chlorophyll content [19,20]. Chlorophyll, which reflects highly in the green spectrum, is a good indicator of many plant stressors with symptoms of foliar chlorosis or yellowing [21]. Unfortunately, the small spectral range of optical cameras make RGB vegetation indices limited in usefulness.
In addition to natural color images, 3D point clouds and highly detailed surface models that provide valuable information about vegetation height and heterogeneity can be computed from RGB images using the photogrammetric technique Structure from Motion (SfM) [22]. The high-resolution representation of crop canopy surfaces presents an opportunity to explore the relationship between canopy structure and important crop characteristics, like stress and productivity. For example, Hunt and Rondon [23] used very high resolution canopy surface models to identify foliar pest damage in potatoes. Other studies have shown success in correlating yield and biomass with structural metrics generally used to characterize geomorphological surfaces [24,25,26]. Parker and Russ [24] measured spatial covariance of LIDAR-derived outer forest canopy through rugosity (standard deviation of canopy height), hypsographs, fractal dimension, integral scale, and elevation relief ratio to characterize conifer forest canopy structural complexity. A similar technique was used by Li et al. [26] and Li, Niu, Chen and Li [25] with photogrammetric point clouds to estimate biomass and leaf area index (LAI) in maize. Studies have also used simple crop height and relative canopy cover to estimate barley and cotton yields [27,28]. Research on methods for characterizing crop canopy structure and the potential for deriving valuable crop information from SfM canopy surface models has been limited, however, and should be further explored.
A common goal within precision agriculture is improving crop yield and farm profitability through the use of technology and data analytics. The current costs and barriers to practical use associated with high spectral resolution imagery and active laser scanning increase the importance of improving the predictive power of inexpensive UAS-acquired data. In this study, we used a small UAS platform equipped with a consumer-grade RGB camera to investigate the use of canopy structural metrics combined with spectral reflectance to monitor the onset of nutrient disorder symptomology in a case study of flue-cured tobacco. This approach goes beyond traditional spectral analysis for remote crop monitoring to explore the relationship between crop health and patterns in canopy height spatial variance measured from high resolution, photogrammetric canopy surface models. Our results suggest that an important relationship exists between relative canopy shape and crop nutrition that can be leveraged to improve the usefulness of low cost UAS for precision agriculture.
2. Materials and Methods
2.1. Study Site
A field experiment took place in Wilson, NC (354742 N lat, 775652 W long) during the 2019 summer growing season to investigate the use of UAS imagery for detecting nutrient disorders in flue-cured tobacco. The study site was located on a commercial farm and was planted and maintained by the farm managers. The site had a mean elevation of 47.5 m and relatively uniform, low gradient topography with mean slope of 1.46 degrees tilted eastward. Soils across the study site were relatively homogeneous sandy loam. Six soil samples evenly distributed across the field were collected and analyzed for nutrient content, pH, humic matter, and cation exchange capacity (CEC) prior to the experiment (NCDA & CS Agronomic Services Division; Raleigh, NC). The soil properties were similar across the samples with an average of 5.68 pH, 3.12 CEC, and 0.32% humic matter. Weather conditions during the experiment were typical of the area’s humid subtropical climate, with an average daily air temperature of 25.6 °C and average daily precipitation of 2.7 mm. During the two weeks prior to the first data collection, the study site received 97 mm of rain. Total rainfall during the remaining four weeks of the experiment was 30 mm.
Flue-cured tobacco seedlings were transplanted on 16 April 2019 into a 0.5 ha field in thirty-six 10 m × 16 m blocks. Each block consisted of four rows with 1.16 m row spacing and 0.58 m in-row spacing between plants. To induce variability and extremes in nutrient availability within the field, 6N-6P-18K fertilizer (Tobacco Super Rainbow; Agrium U.S., Inc., Denver, CO, USA) was applied to the blocks in early May (3–4 true leaves) at four different rates using block randomization. Nine blocks each received 0, 50, 100, or 200% of the recommended fertilizer rate for flue-cured tobacco production as published by Fisher [29]. To induce nutrient disorders, three small strips of twelve plants (approximately 1.7 m × 4.7 m) within each block were given a fertilizer treatment deficient of N, P, or K or a toxic amount of B. Within the blocks fertilized at 0 or 50% rates, the three strips were fertilized with a custom fertilizer made to replicate the 6N-6P-18K fertilizer devoid of either N, P, or K. Within the blocks fertilized at 100 or 200%, the three strips were given an excess application of B at a rate of 4.50, 9.00, or 18.1 in addition to the 6N-6P-18K fertilizer. Figure 1 shows the study site with the block and strip fertilizer treatments. Flowering and topping began on June 15 with all plants topped by 3 July. Chemical sucker control was used to inhibit auxiliary bud growth after topping.
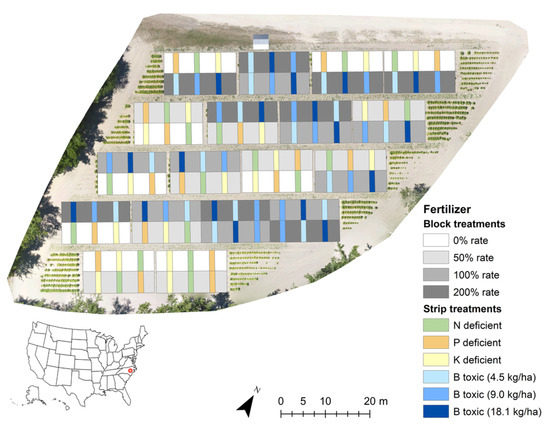
Figure 1.
Field experiment site in Wilson, NC. Flue-cured tobacco was planted in thirty-six blocks each containing three strips fertilized with treatments to induce variability in nutrient availability throughout the 0.5 ha field.
2.2. Data Collection
UAS surveys to collect aerial imagery of the study site were conducted on 19 June, 3 July, and 17 July starting approximately four weeks after the fertilizer treatments were applied. The UAS data were collected by PrecisionHawk (Raleigh, NC, USA) using a DJI Phantom Pro 4 equipped with a 20 mp RGB camera. At least twenty-two images were collected during each survey using a grid flight pattern at approximately 67 m altitude with a nadir camera angle. To ensure matched vegetation features across multiple images, 80% side and forward image overlap was used. Ground control points were not used as the images were initially collected to be used for visual inspection. Errors in X,Y position and elevation were corrected using orthoimagery and LIDAR data as described in Section 2.3.
Foliar tissue samples were collected from each treatment replicate at approximately the same time as the UAS flights by Dr. Josh Henry and field research assistants from the Crop and Soil Sciences and Horticulture Science Departments at NC State. Leaf tissue samples were pooled resulting in three samples per fertilizer treatment to reduce the total number of samples and lab analysis costs. The leaf tissues were dried, ground, and analyzed for elemental nutrient concentrations of N, P, K, and B by AgSource Laboratories (Lincoln, NE, USA).
2.3. Data Processing
Photogrammetry software (Agisoft Metashape, version 1.5.4.8885) was used to process the UAS images into 3D point clouds and orthoimages for the three survey dates. The multi-view stereo images were aligned by matching features in multiple images to create a sparse point cloud. The sparse point cloud was then filtered to include only points with reconstruction uncertainty less than 50 and reprojection error less than 0.35 pixels. A dense point cloud was created using images downscaled by a factor of four (high reconstruction quality setting). Point filtering was disabled to preserve gaps between plants and other heterogeneous features in the point geometry representing the plant canopy (Figure 2). The density of the resulting point clouds was approximately 900 . The average X,Y and Z camera location error was 2.29 m and 0.46 m, respectively. The average point reprojection error was 0.56 pixels.
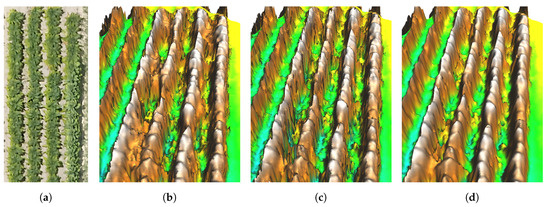
Figure 2.
Comparison of surface models resulting from variations in point cloud filtering in Agisoft Metashape and interpolation smoothing parameters. (a) Orthoimage of tobacco plants represented in surface models shown at right. (b) Noisy surface with poor representation of gaps between plant rows created using mild depth filtering and no surface smoothing. The point filtering algorithm removed important bare ground points between plant rows. (c) Noisy surface with better representation of gaps between plant rows created using no depth filtering and no surface smoothing. (d) Less noisy surface with good representation of gaps between plants created using no depth filtering and smoothing splines with tension.
The point clouds were then interpolated to create smoothed digital surface models (DSM) using a regularized spline with tension method implemented in GRASS GIS 7.8 [30,31]. The tension parameter tunes the surface stiffness and the smoothing parameter controls the resulting surface’s deviation from the point cloud (see the relevant equations and explanation of the parameters in [30,31]). Tension and smoothing parameter settings were iteratively adjusted to reduce surface noise and retain realistic canopy features (tension: 20, smoothing: 5) (Figure 2). A spatial resolution of 0.05 m was used for the interpolated surface model based on point density and plant feature dimensions. To correct errors in X,Y position, the resulting DSMs and UAS-derived orthoimages were georeferenced to 2017 state-wide orthoimagery (0.15 m resolution) [32].
To correct errors in elevation, the DSMs were compared to a 0.05 m resolution digital elevation model (DEM) interpolated from LIDAR bare earth points (9.25 cm vertical linear root mean square error (RMSEz)) collected in 2015 for the NC Floodplain Mapping Program [33]. Orthoimages created from the UAS data were used to identify approximately 30 bare earth points well distributed across the study area that should have elevations values that match the DEM. The DSMs were sampled at each of these bare earth points and the sample point values were interpolated using splines with tension to create smoothed surfaces representing error in the z-values for each DSM (tension: 40, smoothing: 5). The error surfaces were then subtracted from the DSMs to correct the elevation values. The corrected DSMs had bare earth elevation values within ±0.05 m of the DEM. Crop surface models (CSM) with z-values normalized for topography were created by subtracting the bare earth DEM from each DSM. Note that bare earth points from UAS data could also be used to create a DEM when lidar data is not available [34].
A mask was created to exclude non-tobacco features, such as soil, rocks, and other vegetation, from computation of the spectral vegetation index and the structural metrics that were not intended to characterize canopy gaps (described in Section 2.4 and Section 2.5). Features less than 0.2 m in height were considered non-tobacco. This height threshold was effective in removing features that were not of interest while retaining canopy features from the most nutrient deficient plants, which were at least 0.6 m in height at the first survey.
2.4. Canopy Surface Analysis
Using ArcMap 10.7, plot boundaries were drawn around each treatment strip with approximately 0.5 m between each polygon to reduce edge effects, resulting in 4.7 m × 1.2 m areas for each strip. Four plot polygons of equal size were drawn in each treatment block as well (Figure 3). The plot polygons were used to extract pixel values representing crop height in each treatment area and compute metrics quantifying structural characteristics of the canopy. Vertical and horizontal patterns in canopy structure were of interest for their potential to predict crop health. Metrics were chosen to quantify central tendency of crop height, canopy structural complexity, and canopy structural uniformity. Table 1 summarizes the metrics used.

Figure 3.
Plot polygons corresponding to variable nutrient treatments across the study area. The plot polygons were used to extract canopy height and geometry from the canopy surface models.

Table 1.
Summary of canopy metrics computed from unmanned aerial systems (UAS) data.
Nutrient disorders have been shown to correlate with flue-cured tobacco size and shape in multiple prior studies [39,40,41,42]. To quantify plant size and variability in canopy height, mean and standard deviation of height were computed. Skewness and excess kurtosis of the histogram of canopy heights within each plot were used to quantify canopy uniformity and closure [43]. Highly skewed canopy heights may measure uniformity and relative plant shape within a plot (i.e., ratio of height and width of plants). High histogram kurtosis is associated with a very high peak and heavy tails compared to a normal distribution, which may indicate canopy closure, or similar heights across a plot. Low kurtosis indicates a more uniform distribution of heights, which may be a good indicator of the presence of gaps between plants. Rumple index (RI) was used to quantify three-dimensional canopy complexity in both the horizontal and vertical directions [35,44]. RI is a measure of surface roughness, calculated as the ratio between surface area and the two-dimensional projected area on a plane below.
The metrics described thus far do not account for the spatial pattern of canopy structure and cannot, for example, distinguish between clusters of pixels with low heights and dispersed pixels with low heights. To better account for local spatial patterns in canopy structure, canopy relief ratio (CRR) was calculated for a moving window of approximately 0.25 m × 0.25 m (5 × 5 pixels) within each plot [36]. CRR measures how close the mean height is to the minimum and maximum heights within the chosen neighborhood. The neighborhood size was chosen to correspond to one quarter of a single plant to measure variability in relative shape within a plant. Several neighborhood sizes were tested to identify which resulted in metrics that explained the most variability in nutrient concentrations. CRR was calculated as
This metric was intended to measure relative shape of the canopy. Generally, canopy peaks will have CRR values close to 1, valleys will be close 0, and slopes or flat areas will have values centered around 0.5. To summarize the results of the moving window CRR calculation, the median and interquartile range (IQR) for each plot were used.
In addition to CRR, spatial patterns in canopy height were measured using Moran’s I with an approximately 0.55 m × 0.55 m (11 × 11 pixels) Queen’s case weights matrix [37,45,46]. The weights matrix defines the area and direction in which plant heights are expected to be spatially correlated and was chosen to correspond to the in-row plant spacing, or the approximate area of one mature tobacco plant. These metrics were intended to quantify the similarity of local canopy structure across each plot. Plots with repeating patterns of canopy geometry due to uniform plant growth were expected to have high spatial autocorrelation, whereas plots with highly heterogeneous plant sizes and shapes were expected to have low spatial autocorrelation.
2.5. Visible Band Spectral Metrics
Triangular greenness index (TGI) was used to approximate chlorophyll content and vegetation vigor from broadband visible wavelength reflectance. TGI is based on the spectral features of chlorophyll and can be used for crop nitrogen management [19]. TGI was calculated as
where is the center wavelength and is the pixel value of the respective bands. The band center wavelengths used were 670 nm, 550 nm, and 480 nm for red, green, and blue, respectively, as proposed for broadband digital cameras by Hunt et al. [19]. For each UAS survey, TGI was computed for all pixels containing tobacco vegetation using the red, green, and blue bands and summarized per plot using mean and standard deviation.
2.6. Water Flow Index
To account for spatial variability in soil moisture and possible movement of nutrients within the soil caused by water flow, an overland water flow index was computed. The index was derived from an overland flow simulation in GRASS GIS 7.8.0 [38,47]. We simulated a steady state water flow over a 0.05 m resolution LIDAR DEM of the study area resulting in per pixel water accumulation depth [33]. The water depth values were normalized to create an index representing the spatial distribution of water flow for the site. The sum of the per pixel index values was used to summarize water flow for each plot.
2.7. Statistics
The computed canopy metrics were aggregated using the mean value for each combination of three plots used during the foliar tissue sample collection resulting in a single set of canopy metrics per lab sample. The metrics were then z-score = standardized to facilitate comparison of statistical results. The relationship between the canopy metrics and foliar concentrations of N, P, K, and B was evaluated using ordinary least squares regression [48]. To quantify multicollinearity between the regression predictors, the variance inflation factor (VIF), an index measuring the increase in regression coefficient variance caused by collinearity, was computed for each predictor [48]. Any predictor variable with a VIF greater than 4 was omitted from subsequent analysis due to the redundancy of the information provided and to reduce model overfitting [49]. Multicollinear variables removed include height standard deviation and height histogram skewness.
The canopy metrics were then used in ordinary least squares regression to predict not only nutrient concentrations measured at the time of the UAS surveys, but also all prior measurements of nutrient concentrations resulting in six sets of regression models. This was done to investigate the timing of canopy response to the nutrient application. First, the structural and spectral metrics were used in the models separately to predict nutrient concentrations. Then, the combined metrics were used to determine if model fit could be improved by using a combination of structural and spectral information. For each combination of variables, Akaike’s information criteria with small sample bias adjustment (AICc) was used to select the highest quality model to reduce the risk of overfitting [50]. The adjusted coefficient of determination (adj. ) was used to evaluate the models.
3. Results
3.1. Foliar Nutrient Concentrations
A summary of foliar tissue nutrient concentrations and correlation coefficients for the three sample dates are shown in Table 2 and Table 3. The fertilizer treatments applied across the study plots were effective in creating plot-level variability in N, K, and B response. Symptoms of N deficiency were visible early in plant development and were well-captured by each UAS survey. Plots with K deficiency were not observed until after the first UAS survey, with symptoms becoming visible approximately six weeks after the fertilizer treatments were applied. High variability in foliar B concentration was achieved throughout the study site with very high concentrations observed at each sample date. P concentrations, however, were present in the study area soils prior to fertilizer treatments at levels 2–5 times greater than optimal making it impossible to induce a deficit in the plants. P is relatively immobile in soils, which has resulted in a build up of stores in agricultural soils over time caused by fertilizer over-application. As very little variation in foliar P concentrations were observed, the regression models for this nutrient were not informative and therefore not reported here.

Table 2.
Foliar nutrient concentrations.

Table 3.
Correlation matrices of foliar nutrient concentrations.
3.2. UAS-Derived Canopy Metrics
Table 4 shows a summary of the metrics computed to quantify canopy structure and spectral reflectance. Two structural metrics, crop height standard deviation and histogram skewness, were removed from the analysis due to collinearity. The remaining metrics were used to explain variation in foliar N, K, and B concentrations. The standardized regression model coefficients for all models are summarized in Table 5, Table 6 and Table 7.

Table 4.
Summary of UAS-derived canopy metrics.

Table 5.
Summary of standardized coefficients from regression models using canopy structural metrics to predict nutrient concentrations.

Table 6.
Summary of standardized coefficients from regression models using spectral metrics to predict nutrient concentrations.

Table 7.
Summary of standardized coefficients from regression models using a combination of canopy structural and spectral metrics to predict nutrient concentrations.
3.2.1. Mean Crop Height
Mean crop height provided information about the central tendency of height within a plot. It was the most important predictor of N and K concentrations at the last two survey dates (Table 5). Surprisingly, mean height was not important at the earliest growth stage observed. It was also important and positively correlated with B concentrations at the last survey date. These results are consistent with observations made by other researchers that increases in N and B concentrations can lead to an accumulation of plant biomass [27,52,53].
3.2.2. Crop Height Histogram Kurtosis
Kurtosis measured the shape of the distribution of canopy heights with increased histogram kurtosis indicating a sharper peak and more outliers in height compared to a normal distribution of heights. Plots with lower kurtosis tended to have a more uniform distribution of heights with narrow plants and wider gaps between rows (Figure 4). Plots with more canopy closure and fewer ground pixels tended to have high kurtosis. Kurtosis was an important predictor and negatively correlated with foliar concentration of N and K at the last date (Table 5). Kurtosis was important and positively correlation with B at the second survey date.
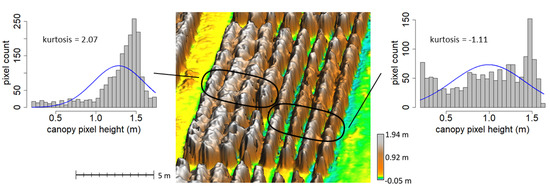
Figure 4.
Tobacco canopy surface model with examples high and low height histogram kurtosis. Plots on the left side have high kurtosis, which corresponded primarily to more canopy closure. Plots on the right side have low kurtosis, which corresponded to more narrow plants with gaps between rows. The blue line in each histogram provides a comparison to a normal distribution.
3.2.3. Rumple Index
Rumple index measured the ratio of the 3D surface area of a volume to its 2D area, with an increase in the index indicating more surface complexity. As RI was computed for each plot of equal 2D area, the index can be interpreted as simply the 3D surface area of the canopy. RI was closely related to the slope of the canopy surface within each plot. Plots with steep canopy slopes (narrow plants with many ground pixels) had high RI and plots with gentle slopes (wide plants with canopy closure) had low RI (Figure 5). RI was one of the most important predictors of N concentrations at the second and third survey dates (Table 5). The positive relationship indicates that as surface area and slopes of the canopy increased, N concentrations increased. Conversely, the pyramid canopy shape symptomatic of N deficiency tended to have gentle slopes with wider plant base and lower RI. RI was negatively correlated with B and K at the first survey date, with more gentle slopes associated with lower concentrations.
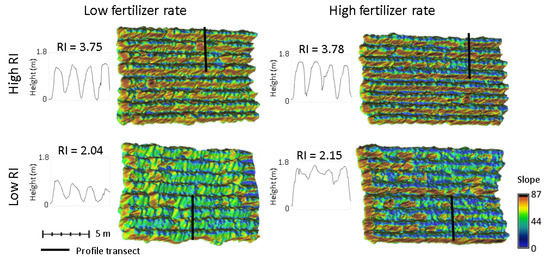
Figure 5.
Slope and RI of tobacco canopy surface models with high and low fertilizer rates. Plots with high RI values are shown in the top row and low RI in the bottom row. Plots with low fertilizer rates are in the left column and high fertilizer rates in the right column. High RI values are associated with steeper canopy slopes (red and yellow), while low RI values are associated with gentle canopy slopes (blue and green). Respective vertical profiles through the canopy are shown with each model.
3.2.4. Canopy Relief Ratio
Canopy relief ratio measured the relative shape of the canopy and was useful for characterizing the ratio of plant width to height and identifying gaps in the canopy. Lower median CRR indicated more narrow plants with less canopy closure (Figure 6). High CRR median was associated with fewer gaps between rows and well defined canopy peaks, in contrast to a rounded canopy. CRR median was important and positively correlated with all nutrients observed at one or more survey dates (Table 5). In particular, it was the most important predictor for K at all dates. It was also the most important structural predictor of N at the first date. These relationships indicate that as nutrient concentrations increase, plants get wider and fill gaps between rows. The consistent positive relationship with K may also be related to K deficiency, which is characterized by leaves that curve downward making the canopy more rounded without a defined peak [42]. When spectral information was added, CRR median was negatively correlated with N at the last two survey dates (Table 7). This may be related to N deficiency symptoms, which include stunting with erect leaves that form a pyramid shape with a sharp canopy peak [42]. CRR interquartile range was associated with the presence of defined peaks as well as gaps between rows. It was important and negatively correlated with N at the first two dates and K at the second date. It was very important and positively correlated with prior B concentrations at the last date.
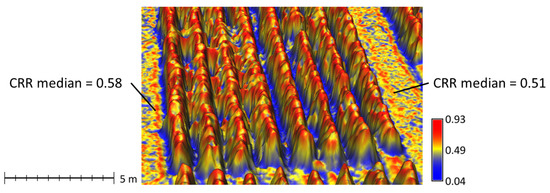
Figure 6.
Tobacco canopy surface model with examples high and low canopy relief ratio (CRR) median. Plots on the left had higher CRR median values and generally had fewer valley pixels (blue) and more slope pixels (yellow). Plots on the right side had more gaps between rows (blue pixels), well-defined peaks (red), and fewer slope pixels (yellow).
3.2.5. Spatial Autocorrelation of Crop Height
Moran’s I measured spatial autocorrelation of crop heights, which characterized canopy surface smoothness or likeness of crop heights within a neighborhood of surface model pixels (Figure 7). Conversely, it also detected the presence of peaks or pits in the canopy. The 0.55 m × 0.55 m neighborhood used to compute spatial autocorrelation corresponded to the approximate size of one healthy plant. Many of the plants, however, were stunted with gaps between rows. The patches of ground areas with similar height between rows resulted in increased Moran’s I values in plots with low canopy closure. Overall, Moran’s I explained the limited variability in nutrient concentrations. Moran’s I was important, and positively correlated with N at the first two dates (Table 5). As N concentrations increased, the plot had more clusters of similar heights and was smoother with fewer peaks or pits. It was important and negatively correlated with prior B concentrations at the last survey date. As B concentrations increased, the canopy was less smooth with more gaps or spikes and has fewer patches of similar heights.
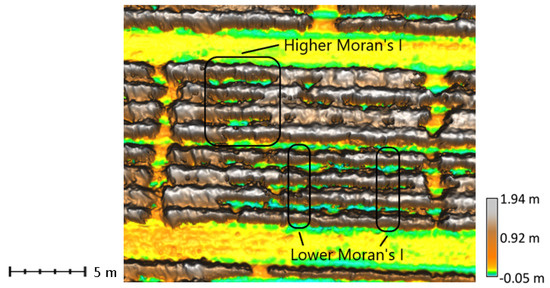
Figure 7.
Canopy surface model of tobacco plots with range of Moran’s I values. Plots in the upper left portion of the block have relatively high Moran’s I (0.74). The plots identified in the lower right have relatively low Moran’s I (0.57).
3.2.6. Water Flow Index
An overland water flow index was included in the regression models to account for topography and how water flow across the field might affect nutrient availability or uptake (Figure 8). The water index was positively correlated with N at the first two survey dates, especially when combined with the spectral metrics (Table 5 and Table 7). There was considerable rainfall over the two weeks between fertilizer application and the first UAS and nutrient survey dates (97 mm). Over the remaining four weeks of the study, there was much less rainfall (30 mm). Although the field was mostly flat, even small changes in elevation can influence the movement of water and soluble nutrients. It is possible that the rainfall early in plant growth influenced the spatial distribution of nutrient and water availability in the field.

Figure 8.
Derived water flow index based on simulated overland water flow.
3.2.7. Triangular Greenness Index
Triangular greenness index measured the similarity of canopy reflectance to the spectral features of chlorophyll and therefore estimated plant chlorophyll content and vigor. TGI mean was important and negatively correlated with all nutrients, although it accounted for almost no variation in B (Table 6). TGI mean was positively correlated with B at the last survey date. Standard deviation of TGI was important and negatively correlated with all of the nutrients, especially at the last survey date, indicating that a wider range of TGI values in a plot is related to lower concentrations of foliar nutrients.
3.3. Overall Relationship between the Crop Canopy Shape, Reflectance, and Nutrient Concentration
The amount of variability explained by the canopy metrics differed by nutrient and developmental stage as shown in Figure 9. Overall, structure had a stronger relationship with N, K, and B concentrations at later growth stages. Visible range spectral reflectance consistently explained variability in N and K concentrations. For nearly all cases, combining spectral and structural information explained more variability in nutrient concentrations than either set of metrics did alone. Moreover, canopy structure and reflectance were more closely related to N and B nutrient concentrations at earlier stages of growth than nutrient concentrations measured at the time of the UAS survey.
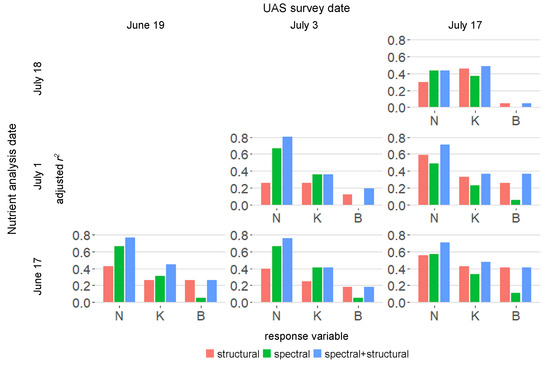
Figure 9.
Adjusted for regression models using canopy structural and spectral metrics to explain foliar concentrations of elemental nutrients in tobacco plants.
3.3.1. Nitrogen
N is the most important nutrient for flue-cured tobacco yield and quality. It is typically applied in time for immediate plant uptake to avoid leaching beyond the root zone. N-deficient plants are characterized by stunting, chlorosis, and upward pointing leaves forming an acute angle with the stalk [39,42]. The structural metrics explained 40% of the variation in N concentrations at the first two growth stages observed (Figure 9). The amount of variability explained increased to as much as 60% at the last observation date. The canopy structure better explained N concentrations measured at the previous date (approximately 2 weeks prior). The visible range spectral metrics explained more variation in N concentrations than structure did overall, with approximately two-thirds of the variability explained at the first two survey dates. At the last survey date, the relationship was slightly weaker and better explained N concentrations measured at previous dates. Combining spectral and structural information strengthened the relationship and explained 75–80% of the variation in N during the first two survey dates. Again, the relationship decreased slightly as the plant matured. This may be explained by the movement of N from leaves to reproductive tissues as the plant matures.
3.3.2. Potassium
K is also an important macronutrient needed for tobacco production. Symptoms of K deficiency include chlorosis that begins on lower leaves and quickly progresses up the plant and leaves with a distinctive downward cupping or umbrella-like shape [39,42]. The canopy structural metrics were able to explain variation in foliar K levels across all dates, with the relationship increasing slightly as the crop matured (Figure 9). Canopy structure explained 26% of K variation at the first date and up to 45% at the last survey date. K deficiency was not achieved until sometime after the first survey date with visible symptoms developing around the same time. This may explain why predictability of K increased over time. K was also the only nutrient that was better predicted using nutrition measurements taken at the same time as the UAS survey. The canopy was able to explain variation in current concentrations of foliar K as well or better than at previous stages of plant development. Visible-range spectral reflectance was able to explain similar amounts of variation in K as canopy structure. The delay in visible deficiency symptoms is reflected in the increase in variation explained by the spectral metrics over time. Combining spectral and structural predictors increased the variation in K explained at the first and last survey dates, with 45% explained at the first date and 49% variation explained at the last date. There was a slight decrease in model fit when predicting K concentrations measured at the second date. All of the other models, however, were able to explain similar amounts of variation ranging from 42% to 51%. The predictability of K using the UAS-derived canopy metrics was the most consistent of the nutrients studied.
3.3.3. Boron
B is an important nutrient for proper development of growing points in tobacco plants. It is needed in very small amounts, however, and can result in reduced leaf quality if over applied [10]. Visible symptoms of B toxicity include a very slow spreading chlorosis on lower leaves, undulating leaf deformity, and curling of leaf edges upward [39]. The canopy structural metrics were able to explain moderate variation in foliar B concentrations (Figure 9). The amount of variation explained at the earliest survey date was 26% and increased to as much as 41% at the latest date when predicting B concentration from the earliest date. B predictability dropped to as low as 5% at the last date when using nutrient concentrations measured at the time of the flight. The structural metrics were much more closely related to B concentrations measured earlier in plant development. This is consistent with other observations that symptoms of B toxicity can take 33 days to become visible [39]. Visible-range spectral reflectance explained almost no variability in B concentrations. Model fit was not improved by combining spectral and structural predictors since the spectral metrics did not explain variability in B.
4. Discussion
In this study, we investigated the relationship between structural and spectral canopy-level metrics derived from a UAS-mounted RGB camera and nutrient concentrations in flue-cured tobacco. The aim of this research was to determine if the plant response to nutrient disorders can be detected from photogrammetric crop surface models and to evaluate the usefulness of structural metrics describing canopy shape and uniformity for improving remote monitoring of crop nutritional status, particularly when used in combination with widely accepted spectral remote sensing techniques. This research demonstrates that information about crop canopy shape and uniformity can provide useful information related to crop health that can be leveraged to improve remote monitoring and modeling for precision agriculture.
This research confirms that a relationship exists between crop canopy structure and nutrient concentrations in plant tissues. Not surprisingly, the strongest relationship observed was between canopy shape and N foliar concentration (adj. = 0.59, increasing to adj. = 0.81 when combined with TGI). Many studies have explored methods for remotely assessing N status and other crop variables closely correlated with N concentration, like leaf area index, above ground biomass, and yield. Work by Li et al. [25,26] found that RI and CRR had high correlation with LAI. These results are consistent with our study, which found that RI, CRR, histogram kurtosis, and mean height were some of the most important predictors of foliar N concentrations. The metrics used in this research and other similar structural measures that quantify the spatial arrangement of heights could be useful for remote approximations of other crop variables correlated with N.
The visible-band spectral vegetation index used in this study—Triangular Greenness Index—provides an approximation of chlorophyll content. The close relationship between N and chlorophyll makes it unsurprising that TGI was limited in explaining concentrations of the other nutrients. Chlorosis, however, is characteristic of K deficiency [39,42], so TGI was able to explain moderate variation in foliar K concentration. As expected, variation in B was not explained by TGI as B toxicity is not closely associated with chlorosis.
Several important decisions about how the metrics were computed affected their ability to explain nutrient concentrations. For example, CRR was more effective when a subplant neighborhood size was used. This suggests that capturing variability in relative shape within a plant influences the usefulness of this metric for characterizing canopy structure. Additionally, the weights matrix used to compute Moran’s I also made this metric more or less useful. The size of the weights matrix should be chosen based on the area in which heights are expected to be spatially autocorrelated. It is also important, however, to consider features that are not of interest, like bare ground, that fall within the matrix and influence the computation. The effectiveness of Moran’s I may be improved by removing soil pixels and using a directional, anisotropic weights matrix to limit the computation to along plant rows for future studies. Nonetheless, lower Moran’s I was useful for identifying plots with B toxicity. This was likely due to plots with toxic B levels being associated with higher overall fertilizer rates and very full, closed canopies with no clusters of ground pixels. Furthermore, plots with closed canopies lacked features with high contrast, like bare earth, that could be used as tie points in the SfM process, which may have increased point cloud errors (unrealistic peaks and pits) further reducing spatial autocorrelation. Further research should be done to understand how this approach is sensitive to decisions about the window sizes and weight matrices used.
The regression models predicting N and B foliar concentrations all improved when using nutrient concentrations measured 2–4 weeks prior to the UAS survey. While the direct cause of this effect remains unclear, a few possible explanations warrant discussion. N is very mobile within the plant, so this preference for past nutrient measurements could be explained by the movement of these nutrients to other, unsampled parts of the plants, particularly reproductive tissue [54]. The sharp decrease in correlation between nutrient concentrations at the second and third foliar sample dates could also be related to nutrient mobility (Table 3). Another potential explanation for the increased relationship between the canopy and past nutrient concentrations is an accumulation of symptomlogy over time making the effects of a disorder more apparent. There also could be a delay in appearance of symptoms measurable by the structural and spectral metrics. B toxicity in particular has been shown to take over a month to develop visible symptoms [39]. As this delay pattern was observed for two of the three nutrients studied, further investigation should be completed to understand the cause and practical implications this has for precision agriculture or rapid phenotyping applications.
Symptoms of N and K deficiencies in flue-cured tobacco described by McMurtrey and Henry et al. [39,42] were well captured by the structural metrics used in this study and the distinct features of the deficiencies can be used to differentiate each. N deficiencies are associated with chlorosis, stunting, and erect leaves that form an acute angle with the stalk. K deficiencies are also associated with chlorosis and stunting, but in contrast to N deficiencies, leaf deformation is characterized by a downward cupping or umbrella-like shape. This explains why the most important structural metric for predicting K concentrations was CRR. K-deficient plants with downward curving leaves are limited in width and less likely to fill spaces between rows, resulting in more valleys in the canopy shape, which have CRR close to zero and lower median CRR values. Furthermore, the downward curved leaves result in a rounded canopy with fewer peaks, which further lowers median CRR values. Whereas high height histogram kurtosis was one of the most important predictors of N deficiency due to leaves that stand at an acute angle relative to the stalk creating a relatively short, pyramid shaped canopy with fewer gaps between rows. Figure 10 illustrates the differences in canopy shape for N and K deficiencies. Kurtosis and CRR in combination with mean height, which captures stunting, were effective in distinguishing N and K deficiencies. If spectral reflectance information is also considered, it is possible that N and P deficiencies could also be distinguished due to the lack of chlorosis associated with P deficiencies [39,42]. Future experiments to observed P deficiencies in field-grown tobacco are needed to test this.

Figure 10.
Canopy surface model with nutrient deficient plots. The K-deficient plot in the upper right has a rounded canopy shape with minimal closure between rows resulting in lower median CRR. The N-deficient plot to the left has a pyramid shape with sharper peaks and is generally stunted resulting in high height histogram kurtosis and low mean height.
Many studies have focused on validating the accuracy of measurements taken from photogrammetric surface models, like crop height and volume, through field measurements and precise ground control [53,55,56,57]. While the importance of accuracy for many measurements taken from canopy surface models is clear, the measurements of interest in this study focus on relative shape of the canopy rather than absolute quantities. Point cloud quality, however, is important to ensure that the reconstruction of the canopy shape is representative of reality. Decisions made during image acquisition and processing, like camera angle, image overlap, flight time of day, altitude, point filtering, and surface interpolation, all have an impact on feature reconstruction. For example, the challenge faced by the SfM algorithm when distinguishing between low-contrast features like plants, shadows, and dark, moist soil was apparent in the June 17 CSM. The canopy appears more closed with fewer soil pixels compared to the 3 July CSM, which was created from images with high contrast between features due to better lighting and lower soil moisture. Furthermore, oblique imagery, which has been shown to improve reconstruction of vertical features, like buildings, forests, and steep terrain [58,59], was not collected for use in this study. Future implementation of this approach should incorporate oblique imagery during point cloud generation to improve representation of canopy features, especially along plant row edges. Several studies [55,58,60,61,62,63] have evaluated the impact of these considerations on feature reconstruction, but further research is needed to understand how sensitive the canopy structural metrics used in this study are to data acquisition and processing parameters. However, the relatively strong, consistent relationships between canopy structure and nutrients observed across all dates suggest that trends in canopy shape are being represented well enough in the data to provide meaningful, useful information.
5. Conclusions
In this study, we developed a methodology for extracting crop canopy characteristics from high-resolution, photogrammetric canopy surface models and demonstrated how these characteristics can be used to improve remote monitoring of crop nutrient status. The strength of this approach is its use of both 3D canopy geometry and spectral reflectance derived from very low cost, ubiquitous UAS with a consumer-grade RGB camera. Combining spectral and structural canopy information improved model fit in nearly every case observed, making a strong case for including structural metrics in models used to remotely estimate crop variables. The relationship between canopy structure measured from point clouds and crop stress should be further explored as we may be able to leverage this relationship as technologies for producing more precise point clouds become more readily available (e.g., active LIDAR sensors optimized for use with UAS). In the meantime, useful information about canopy structure can be extracted from photogrammetric point clouds to improve remote estimates of nutritional status and identify areas that warrant further ground-based observation and evaluation. Further investigation should also be done to explore how canopy structure varies in response to different types of stress to attempt to remotely distinguish the cause of plant stress without destructive, specialized testing. High spatial and temporal resolution data on 3D canopy geometry opens up new opportunities to explore patterns in plant responses to stress that could provide useful evidence to support management decisions or rapid phenotyping.
Author Contributions
Conceptualization, K.M. and H.M.; Methodology, K.M., H.M., J.B.H., B.W., and M.C.V.; Validation, K.M. and H.M.; Formal analysis, K.M.; Investigation, K.M. and J.B.H.; Resources, K.M., J.B.H., B.W., and M.C.V.; Writing—original draft preparation, K.M.; Writing—review and editing, K.M., H.M., J.B.H., M.C.V., and A.S.H.; visualization, K.M.; funding acquisition, K.M, J.B.H., B.W., and M.C.V. All authors have read and agreed to the published version of the manuscript.
Funding
Development of the research methodology was partially funded by the North Carolina Space Grant. The field experiment and data collection were funded by the North Carolina Tobacco Foundation, Inc.
Acknowledgments
Thanks to Vick Family Farms of Wilson, NC for donating the field space and planting and maintaining the research site. Thanks to Norman Harrell and the Wilson County Cooperative Extension Center for their help working with the farm. Thanks to technicians Jeremy Machacek, Ingram McCall, and Scott Whitley for managing research preparation. Last, thank you to the graduate and undergraduate students for their contributions applying treatments, collecting data, and more: Jeb Bullard, Drew Clapp, Camden Finch, Paige Herring, Nathan Jahnke, Nick Manning, Channie Renn, Maggie Short, Drake Stevens, and Patrick Veazie.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| UAS | Unmanned aerial system |
| N | Nitrogen |
| P | Phosphorus |
| K | Potassium |
| B | Boron |
| NDVI | Normalized Difference Vegetation Index |
| VARI | Visible Atmospheric Resistance Index |
| TGI | Triangular Greenness Index |
| RGB | Red Green Blue |
| SfM | Structure from Motion |
| LAI | Leaf area index |
| CEC | Cation exchange capacity |
| DSM | Digital surface model |
| DEM | Digital elevation model |
| RMSEz | Root mean squared error in z direction |
| CSM | Crop surface model |
| RI | Rumple index |
| CRR | Canopy relief ratio |
| IQR | Interquartile range |
| VIF | Variable inflation factor |
| AIC | Akaike’s information criteria |
References
- Stafford, J.V. Implementing Precision Agriculture in the 21st Century. J. Agric. Eng. Res. 2000, 76, 267–275. [Google Scholar] [CrossRef]
- Hunt, E.R.; Daughtry, C.S.T. What good are unmanned aircraft systems for agricultural remote sensing and precision agriculture? Int. J. Remote Sens. 2018, 39, 5345–5376. [Google Scholar] [CrossRef]
- Zhang, C.; Kovacs, J. The application of small unmanned aerial systems for precision agriculture: A review. Precis. Agric. 2012, 13, 693–712. [Google Scholar] [CrossRef]
- Corti, M.; Cavalli, D.; Cabassi, G.; Vigoni, A.; Degano, L.; Marino Gallina, P. Application of a low-cost camera on a UAV to estimate maize nitrogen-related variables. Precis. Agric. 2019, 20, 675–696. [Google Scholar] [CrossRef]
- Cilia, C.; Panigada, C.; Rossini, M.; Meroni, M.; Busetto, L.; Amaducci, S.; Boschetti, M.; Picchi, V.; Colombo, R. Nitrogen Status Assessment for Variable Rate Fertilization in Maize through Hyperspectral Imagery. Remote Sens. 2014, 6, 6549–6565. [Google Scholar] [CrossRef]
- Maresma, A.; Lloveras, J.; Martínez-Casasnovas, J.A. Use of Multispectral Airborne Images to Improve In-Season Nitrogen Management, Predict Grain Yield and Estimate Economic Return of Maize in Irrigated High Yielding Environments. Remote Sens. 2018, 10, 543. [Google Scholar] [CrossRef]
- Berger, K.; Verrelst, J.; Féret, J.B.; Wang, Z.; Wocher, M.; Strathmann, M.; Danner, M.; Mauser, W.; Hank, T. Crop nitrogen monitoring: Recent progress and principal developments in the context of imaging spectroscopy missions. Remote Sens. Environ. 2020, 242, 111758. [Google Scholar] [CrossRef]
- Mitra, G. Essential plant nutrients and recent concepts about their uptake. In Essential Plant Nutrients, 1st ed.; Springer: Cham, Switzerland, 2017; pp. 3–36. [Google Scholar] [CrossRef]
- Henry, J.B.; Vann, M.C.; Lewis, R.S. Agronomic Practices Affecting Nicotine Concentration in Flue-Cured Tobacco: A Review. Agron. J. 2019, 111, 3067–3075. [Google Scholar] [CrossRef]
- Ruiz, J.M.; Lopez-Lefebre, L.R.; Sanchez, E.; Rivero, R.M.; Garcia, P.C.; Romero, L. Preliminary studies on the influence of boron on the foliar biomass and quality of tobacco leaves subjected to NO3- fertilisation. J. Sci. Food Agric. 2001, 81, 739–744. [Google Scholar] [CrossRef]
- Tariq, M.; Akbar, A.; Lataf-ul-Haq.; Khan, A. Comparing Application Methods for Boron Fertilizer on the Yield and Quality of Tobacco (Nicotiana tabacum L.). Commun. Soil Sci. Plant Anal. 2010, 41, 1525–1537. [Google Scholar] [CrossRef]
- Römheld, V. Diagnosis of deficiency and toxicity of nutrients. In Marschner’s Mineral Nutrition of Higher Plants; Elsevier Science & Technology: San Diego, CA, USA, 2011. [Google Scholar]
- Stroppiana, D.; Migliazzi, M.; Chiarabini, V.; Crema, A.; Musanti, M.; Franchino, C.; Villa, P. Rice yield estimation using multispectral data from UAV: A preliminary experiment in northern Italy. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 4664–4667. [Google Scholar] [CrossRef]
- Bolton, D.K.; Friedl, M.A. Forecasting crop yield using remotely sensed vegetation indices and crop phenology metrics. Agric. For. Meteorol. 2013, 173, 74–84. [Google Scholar] [CrossRef]
- Stanton, C.; Starek, M.J.; Elliott, N.; Brewer, M.; Maeda, M.M.; Chu, T. Unmanned aircraft system-derived crop height and normalized difference vegetation index metrics for sorghum yield and aphid stress assessment. J. Appl. Remote Sens. 2017, 11, 026035. [Google Scholar] [CrossRef]
- Severtson, D.; Callow, N.; Flower, K.; Neuhaus, A.; Olejnik, M.; Nansen, C. Unmanned aerial vehicle canopy reflectance data detects potassium deficiency and green peach aphid susceptibility in canola. Precis. Agric. 2016, 17, 659–677. [Google Scholar] [CrossRef]
- Henry, J.B. Characterization of Tobacco Nutrient Disorders via Remote Sensing. Ph.D. Thesis, North Carolina State University, Raleigh, NC, USA, 2019. [Google Scholar]
- Adão, T.; Hruška, J.; Pádua, L.; Bessa, J.; Peres, E.; Morais, R.; Sousa, J. Hyperspectral Imaging: A Review on UAV-Based Sensors, Data Processing and Applications for Agriculture and Forestry. Remote Sens. 2017, 9, 1110. [Google Scholar] [CrossRef]
- Hunt, E.R.; Doraiswamy, P.C.; McMurtrey, J.E.; Daughtry, C.S.T.; Perry, E.M.; Akhmedov, B. A visible band index for remote sensing leaf chlorophyll content at the canopy scale. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 103–112. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel algorithms for remote estimation of vegetation fraction. Remote Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef]
- Liew, O.W.; Chong, P.C.J.; Li, B.; Asundi, A.K. Signature Optical Cues: Emerging Technologies for Monitoring Plant Health. Sensors 2008, 8, 3205–3239. [Google Scholar] [CrossRef]
- Carrivick, J.; Smith, M.; Quincey, D. Structure from Motion in the Geosciences, 1st ed.; Number Book, Whole in New Analytical Methods in Earth and Environmental Science; Wiley-Blackwell: Hoboken, NJ, USA, 2016. [Google Scholar]
- Hunt, E.R.; Rondon, S.I. Detection of potato beetle damage using remote sensing from small unmanned aircraft systems. J. Appl. Remote Sens. 2017, 11, 026013. [Google Scholar] [CrossRef]
- Parker, G.G.; Russ, M.E. The canopy surface and stand development: Assessing forest canopy structure and complexity with near-surface altimetry. For. Ecol. Manag. 2004, 189, 307–315. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Chen, H.; Li, D. Characterizing canopy structural complexity for the estimation of maize LAI based on ALS data and UAV stereo images. Int. J. Remote Sens. 2017, 38, 2106–2116. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Chen, H.; Li, D.; Wu, M.; Zhao, W. Remote estimation of canopy height and aboveground biomass of maize using high-resolution stereo images from a low-cost unmanned aerial vehicle system. Ecol. Indic. 2016, 67, 637–648. [Google Scholar] [CrossRef]
- Bendig, J.; Bolten, A.; Bennertz, S.; Broscheit, J.; Eichfuss, S.; Bareth, G. Estimating Biomass of Barley Using Crop Surface Models (CSMs) Derived from UAV-Based RGB Imaging. Remote Sens. 2014, 6, 10395–10412. [Google Scholar] [CrossRef]
- Chu, T.; Chen, R.; Landivar, J.A.; Maeda, M.M.; Yang, C.; Starek, M.J. Cotton growth modeling and assessment using unmanned aircraft system visual-band imagery. J. Appl. Remote Sens. 2016, 10, 036018-17. [Google Scholar] [CrossRef]
- Fisher, L.R. Flue-Cured Tobacco Guide, rev. ed.; North Carolina Cooperative Extension: Raleigh, NC, USA, 2019. [Google Scholar]
- Mitasova, H.; Mitas, L.; Harmon, R.S. Simultaneous spline approximation and topographic analysis for lidar elevation data in open-source GIS. IEEE Geosci. Remote Sens. Lett. 2005, 2, 375–379. [Google Scholar] [CrossRef]
- Mitas, L.; Mitasova, H.; Kosinovsky, I.; McCauley, D.; Hofierka, J.; Zubal, S.; Lacko, M. GRASS GIS: V.surf.rst Module; GRASS: Raleigh, NC, USA, 2018. [Google Scholar]
- North Carolina Geographic Information Coordinating Council. NC OneMap Orthoimagery; North Carolina Geographic Information Coordinating Council: Raleigh, NC, USA, 2017. [Google Scholar]
- North Carolina Emergency Management. NC Floodplain Mapping Program QL2 LiDAR; North Carolina Emergency Management: Raleigh, NC, USA, 2015. [Google Scholar]
- Jensen, J.; Mathews, A. Assessment of image-based point cloud products to generate a bare earth surface and estimate canopy heights in a woodland ecosystem. Remote Sens. 2016, 8, 50. [Google Scholar] [CrossRef]
- Jenness, J.S. Calculating landscape surface area from digital elevation models. Wildl. Soc. Bull. 2004, 32, 829–839. [Google Scholar] [CrossRef]
- Pike, R.J.; Wilson, S.E. Elevation-Relief Ratio, Hypsometric Integral, and Geomorphic Area-Altitude Analysis. Geol. Soc. Am. Bull. 1971, 82, 1079. [Google Scholar] [CrossRef]
- Moran, P.A.P. Notes of continuous stochastic phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef]
- Mitasova, H.; Thaxton, C.; Hofierka, J.; McLaughlin, R.; Moore, A.; Mitas, L. Path sampling method for modeling overland water flow, sediment transport, and short term terrain evolution in Open Source GIS. In Developments in Water Science; Elsevier B.V.: Amsterdam, The Netherlands, 2004; Volume 55, pp. 1479–1490. [Google Scholar] [CrossRef]
- Henry, J.B.; Vann, M.; McCall, I.; Cockson, P.; Whipker, B.E. Nutrient Disorders of Burley and Flue-Cured Tobacco: Part 2—Micronutrient Disorders. Crop. Forage Turfgrass Manag. 2018, 4, 1–7. [Google Scholar] [CrossRef]
- Henry, J.B.; Vann, M.; McCall, I.; Cockson, P.; Whipker, B.E. Nutrient Disorders of Burley and Flue-Cured Tobacco: Part 1—Macronutrient Deficiencies. Crop Forage Turfgrass Manag. 2018, 4, 1–8. [Google Scholar] [CrossRef]
- Raper, C.D.; Smith, W.T. Factors Affecting the Development of Flue-cured Tobacco Grown in Artificial Environments. V. Effects of Humidity and Nitrogen Nutrition1. Agron. J. 1975, 67, 307–312. [Google Scholar] [CrossRef]
- McMurtrey, J.E. Symptoms on Field-Grown Tobacco Characteristic of the Deficient Supply of Each of Several Essential Chemical Elements; Technical Report 612; United States Department of Agriculture: Washington, DC, USA, 1938. [Google Scholar]
- Peterson, B.G.; Carl, P. PerformanceAnalytics: Econometric Tools for Performance and Risk Analysis; CRANE Co.: Stamford, CT, USA, 2020. [Google Scholar]
- Roussel, J.R.; Auty, D. lidR: Airborne LiDAR Data Manipulation and Visualization for Forestry Applications; CRANE Co.: Stamford, CT, USA, 2019. [Google Scholar]
- Hijmans, R.J. Raster: Geographic Data Analysis and Modeling; CRANE Co.: Stamford, CT, USA, 2017. [Google Scholar]
- Anselin, L. Local Indicators of Spatial Association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Mitasova, H.; Hofierka, J.; Thaxton, C. GRASS GIS: R.sim.water Module; GRASS: Raleigh, NC, USA, 2019. [Google Scholar]
- Hebbali, A. olsrr: Tools for Building OLS Regression Models, R package version 0.5.3; GRASS: Raleigh, NC, USA, 2020. [Google Scholar]
- Hebbali, A. Collinearity Diagnostics, Model Fit & Variable Contribution; GRASS: Raleigh, NC, USA, 2020. [Google Scholar]
- Wada, Y.; Wisser, D.; Eisner, S.; Flörke, M.; Gerten, D.; Haddeland, I.; Hanasaki, N.; Masaki, Y.; Portmann, F.T.; Stacke, T.; et al. Multimodel projections and uncertainties of irrigation water demand under climate change. Geophys. Res. Lett. 2013, 40, 4626–4632. [Google Scholar] [CrossRef]
- Campbell, C.R. Tobacco, Flue-cured. In Reference Sufficiency Ranges for Plant Analysis in the Southern Region of the United States; Number Bulletin #394 in Southern Cooperative Series; North Carolina Department of Agriculture and Consumer Services Agronomic Division: Raleigh, NC, USA, 2000. [Google Scholar]
- López-Lefebre, L.R.; Rivero, R.M.; García, P.C.; Sánchez, E.; Ruiz, J.M.; Romero, L. Boron Effect on Mineral Nutrients of Tobacco. J. Plant Nutr. 2002, 25, 509–522. [Google Scholar] [CrossRef]
- Bendig, J.; Yu, K.; Aasen, H.; Bolten, A.; Bennertz, S.; Broscheit, J.; Gnyp, M.L.; Bareth, G. Combining UAV-based plant height from crop surface models, visible, and near infrared vegetation indices for biomass monitoring in barley. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 79–87. [Google Scholar] [CrossRef]
- Ohyama, T. Nitrogen as a major essential element of plants. In Nitrogen Assimilation in Plants; Research Signpost: New York, NY, USA, 2010; pp. 1–18. [Google Scholar]
- Kameyama, S.; Sugiura, K. Estimating Tree Height and Volume Using Unmanned Aerial Vehicle Photography and SfM Technology, with Verification of Result Accuracy. Drones 2020, 4, 19. [Google Scholar] [CrossRef]
- Fawcett, D.; Azlan, B.; Hill, T.C.; Kho, L.K.; Bennie, J.; Anderson, K. Unmanned aerial vehicle (UAV) derived structure-from-motion photogrammetry point clouds for oil palm (Elaeis guineensis) canopy segmentation and height estimation. Int. J. Remote Sens. 2019, 40, 7538–7560. [Google Scholar] [CrossRef]
- Jayathunga, S.; Owari, T.; Tsuyuki, S. Evaluating the Performance of Photogrammetric Products Using Fixed-Wing UAV Imagery over a Mixed Conifer–Broadleaf Forest: Comparison with Airborne Laser Scanning. Remote Sens. 2018, 10, 187. [Google Scholar] [CrossRef]
- Díaz, G.M.; Mohr-Bell, D.; Garrett, M.; Muñoz, L.; Lencinas, J.D. Customizing unmanned aircraft systems to reduce forest inventory costs: Can oblique images substantially improve the 3D reconstruction of the canopy? Int. J. Remote Sens. 2020, 41, 3480–3510. [Google Scholar] [CrossRef]
- Nesbit, P.R.; Hugenholtz, C.H. Enhancing UAV–SfM 3D Model Accuracy in High-Relief Landscapes by Incorporating Oblique Images. Remote Sens. 2019, 11. [Google Scholar] [CrossRef]
- Dandois, J.P.; Baker, M.; Olano, M.; Parker, G.G.; Ellis, E.C. What is the Point? Evaluating the Structure, Color, and Semantic Traits of Computer Vision Point Clouds of Vegetation. Remote Sens. 2017, 9, 355. [Google Scholar] [CrossRef]
- Dandois, J.; Olano, M.; Ellis, E. Optimal Altitude, Overlap, and Weather Conditions for Computer Vision UAV Estimates of Forest Structure. Remote Sens. 2015, 7, 13895–13920. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S. Mitigating systematic error in topographic models derived from UAV and ground-based image networks. Earth Surf. Process. Landforms 2014, 39, 1413–1420. [Google Scholar] [CrossRef]
- Cunliffe, A.M.; Brazier, R.E.; Anderson, K. Ultra-fine grain landscape-scale quantification of dryland vegetation structure with drone-acquired structure-from-motion photogrammetry. Remote Sens. Environ. 2016, 183, 129–143. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).