1. Introduction
Laser scanning is a well-established and consolidated technology used extensively for environmental monitoring and mapping. In forest monitoring and inventories, airborne laser scanning (ALS) started to be used since 1990s [
1] with focus on tree height measurements (e.g., [
2]), individual tree identification (e.g., [
3,
4,
5]), canopy structure assessment (e.g., [
6]), forest volume estimation (e.g., [
7,
8,
9]) and stand basal area estimation (e.g., [
10,
11]). The applications of LiDAR (Light Detection and Ranging) technology have rapidly developed and today ALS systems are routinely used over extensive areas to collect stand level and regional wall-to-wall forest mensuration data for forest management [
12,
13]. In contexts where forest cover is fragmented, common in Europe, ALS has not yet become a standard methodology for forest inventory [
14]: high survey deployment costs, the requirement for field measured calibration plots and short flying season in some areas have restricted the usage of ALS surveys in support of key management decisions [
15].
The parallel development of UAVs (unmanned aerial vehicles) for environmental monitoring, of compact laser scanners, miniaturized global navigation satellite system (GNSS) receivers and inertial navigation system (INS) and mini computers allowed the integration and deployment of UAV set up with LiDAR sensors [
16,
17]. Diffusion of UAV laser scanners is however weak compared to other sensors mounted on UAV, such as RGB cameras, multispectral and thermal sensors [
18], due to the higher cost of laser scanners, and to the complexity of the integration of laser sensors with attitude and heading reference system (AHRS) and GNNS receivers. The strength of UAV-LS with respect to ALS is the greater flexibility in planning the survey, especially when frequent flight repetitions over the same target area are needed. Moreover, products derived from the point cloud acquired with laser scanning (e.g., canopy height models, CHMs) outperform the same products obtained from the point cloud derived using the “structure-from-motion” photogrammetry [
19] especially in forests with variable canopy densities [
20]. It is known that digital aerial photography (DAP) major advantage is its scalability in enhanced forest inventories where manned aircrafts are required to cover extensive areas that are out-of-range of UAVs. Given that DAP does not rely on the reflection of laser pulses, survey flights can be higher and faster than ALS ones, covering larger areas and costing one-half to one-third less than ALS flights [
21,
22]. DAP can rely on GPU-optimization for the image-matching algorithms and a high automation of the workflow [
23] making the cloud-point generation and processing easier for the end user. Still, DAP is limited to imaging the canopy envelope [
24] given that there is no penetration as compared with laser pulses. DAP performances have been compared with ALS in characterizing canopy structures and canopy gaps even in complex forests, obtaining comparable (albeit inferior) performances. Refs. [
25,
26,
27] found very comparable correlation coefficients for CHM vs. measured data for both ALS and DAP. In the work of [
27] a key finding was that polygons classified by ALS and DAP segmentation were different in terms of shape and size even if the detection rates and evaluated tree heights were comparable. ALS segmentation tended to under-segment and under-detect trees, while DAP segmentation tended toward over-segmentation. For ground normalization, however, DAP data require a reliable high-resolution digital elevation model (DEM) that cannot be derived by DAP data themselves in areas with a certain degree of canopy cover [
28,
29]. The elevation model often requires a dedicated ALS or UAV acquisition in order to properly correct DAP data for segmentation [
22,
25,
27] and remains one of the key weaknesses of DAP. DAP, however, remains an appealing approach for repeated sampling of extended areas where UAV-LS or ALS scanning is not feasible, due to its cost and complexity of data processing.
There is still limited scientific information about the practical accuracy of point clouds collected with UAVs equipped with LiDAR systems. [
30] analyzed several aspects of the UAV-LS point cloud generation performance based on flights conducted with HDL-32E and VLP-16 laser scanners (Velodyne LiDAR, Inc., USA), reporting a limited performance of the navigation sensors used for UAV trajectory reconstruction. The outcomes of [
31] highlighted that the accuracy of the UAV-LS point cloud, though lower than that of a point cloud obtained from optical images, may be still sufficient for certain mapping applications especially where optical imaging is not efficient. Another experiment of [
31] conducted to test the performance of UAV equipped with HDL-32E LiDAR sensor (Velodyne LiDAR, Inc., USA) confirmed that the trajectory reconstruction, especially the altitude, has a significant impact on the point cloud accuracy. Estimated absolute accuracy of point clouds collected during test flights was reported to be lower than 10 cm, fitting mapping-grade category. [
32] assessed the accuracy of a low-cost mapping UAV-LS and found the altimetric accuracy with this system being around 30 cm, which is acceptable for forest applications.
Nevertheless, an increasing number of research activities that applied UAV-LS in the forestry field are carried on because there is a growing interest for operational use of UAV-LS. Ref. [
33] tested a technology that facilitates mobile surveys in GPS-denied below-canopy forest environments mounting a UTM-30LX LiDAR sensor (Hokuyo Automatic Co., LTD, Japan). Ref. [
34] used UAV-based LiDAR data acquired by a VUX-1UAV laser scanner (Riegl Laser Measurement Systems GmbH, Austria) over a forest area to extract detailed forest and ground information finding that UAV-based laser scanning is providing both high-quality forest structural and terrain elevation information. Ref. [
35] estimated the DBH from a UAV point cloud acquired through a VUX-SYS LiDAR sensor (Riegl Laser Measurement Systems GmbH, Austria) based on modeling the relevant part of the tree stem with a cylinder. Ref. [
36] proposed a new concept of autonomous forest field investigation to collect data above and inside the forest canopy by integrating an autonomous driving UAV with a Puck LITE laser scanner (Velodyne LiDAR, Inc., USA). Ref. [
37] used an integrated UAV-LS system to collect and process LiDAR data for biodiversity studies (i.e., 3D habitat mapping) in three forest ecosystems using a Puck VLP-16 laser scanner (Velodyne LiDAR, Inc., USA). Ref. [
38] tested a LiDAR-hyperspectral image fusion method in treated and control forests with varying tree density and canopy cover as well as in an ecotone environment, integrating an HDL-32E LiDAR sensor (Velodyne LiDAR, Inc., USA). Ref. [
39] estimated tree volume through quantitative structure modeling applied on UAV-LS data acquired with a RIEGL Ri-COPTER with VUX-1UAV (Riegl Laser Measurement Systems GmbH, Horn, Austria). Ref. [
40] explored a carbon model applied to CHM produced using a cloud point collected by UAV-LS over a deciduous forest using a Velodyne VLP-16 (Velodyne LiDAR, Inc., USA) LiDAR sensor. Ref. [
41] estimated the DBH of urban trees by a linear regression model based on variables extracted from a CHM obtained from the UAV-based laser scanning system developed by [
32].
Most recent studies were aimed to assess whether UAV-LS point clouds are qualified for individual tree mapping and modeling in various forest stands [
42], how their accuracies are by comparison with terrestrial laser scanning [
43], whether DBH and tree position estimation algorithms developed for ALS are suitable for UAV-LS data [
44] and finally, how the level of processing automation impacts the tree mapping and modeling accuracy [
15]. While the accuracy of UAV point clouds is overall high [
32], the evaluation of further data processing algorithms for higher level products delivery in forestry is necessary for a comprehensive assessment of UAV-LS especially in complex forest structures. For example, Ref. [
44] evaluated five existing segmentation algorithms (i.e., raster-based region growing, local maxima centroidal Voronoi tessellation, point-cloud level region growing, marker controlled watershed and continuously adaptive mean shift) to determine the most suitable method for individual tree detection across a species-diverse forest.
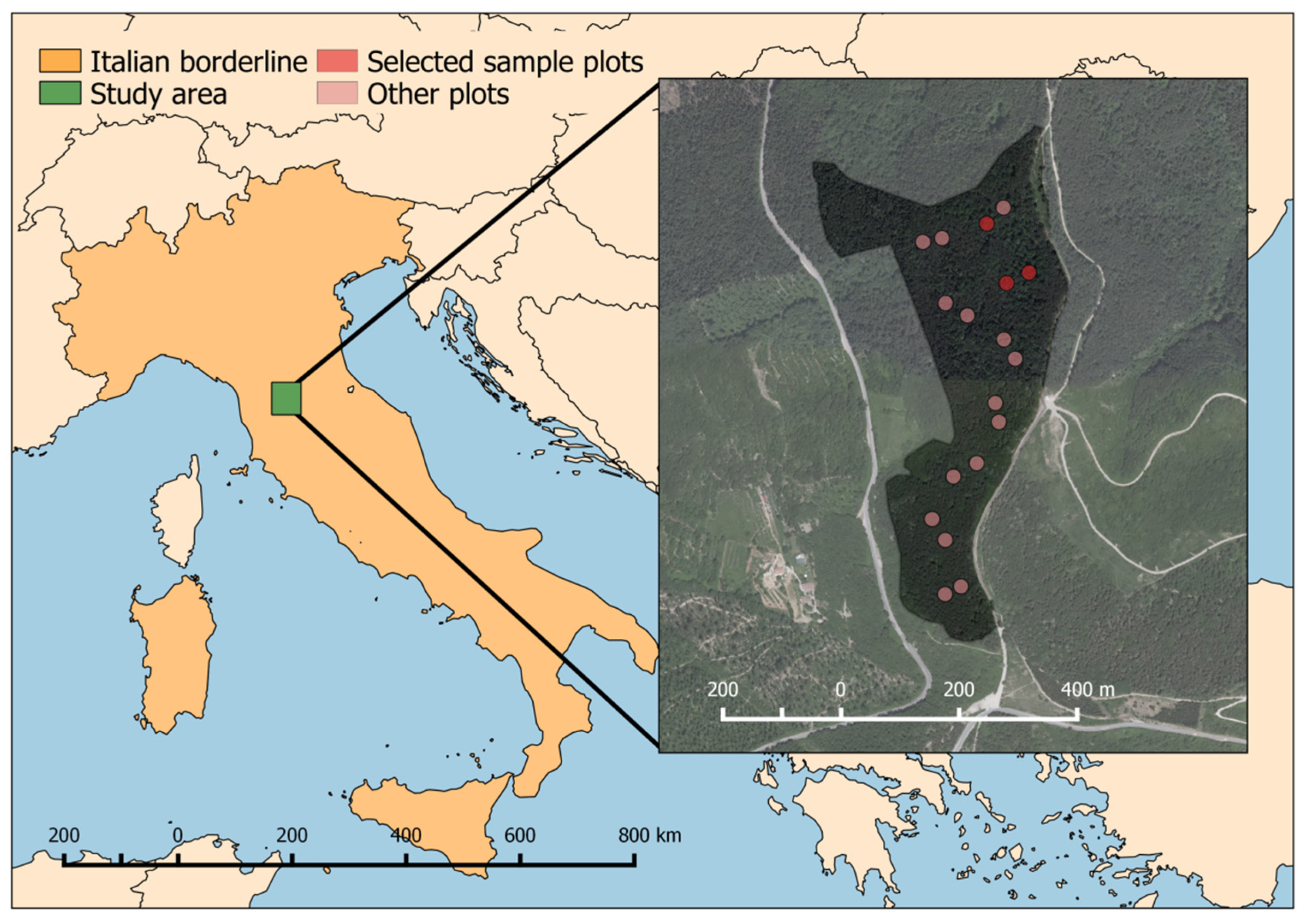
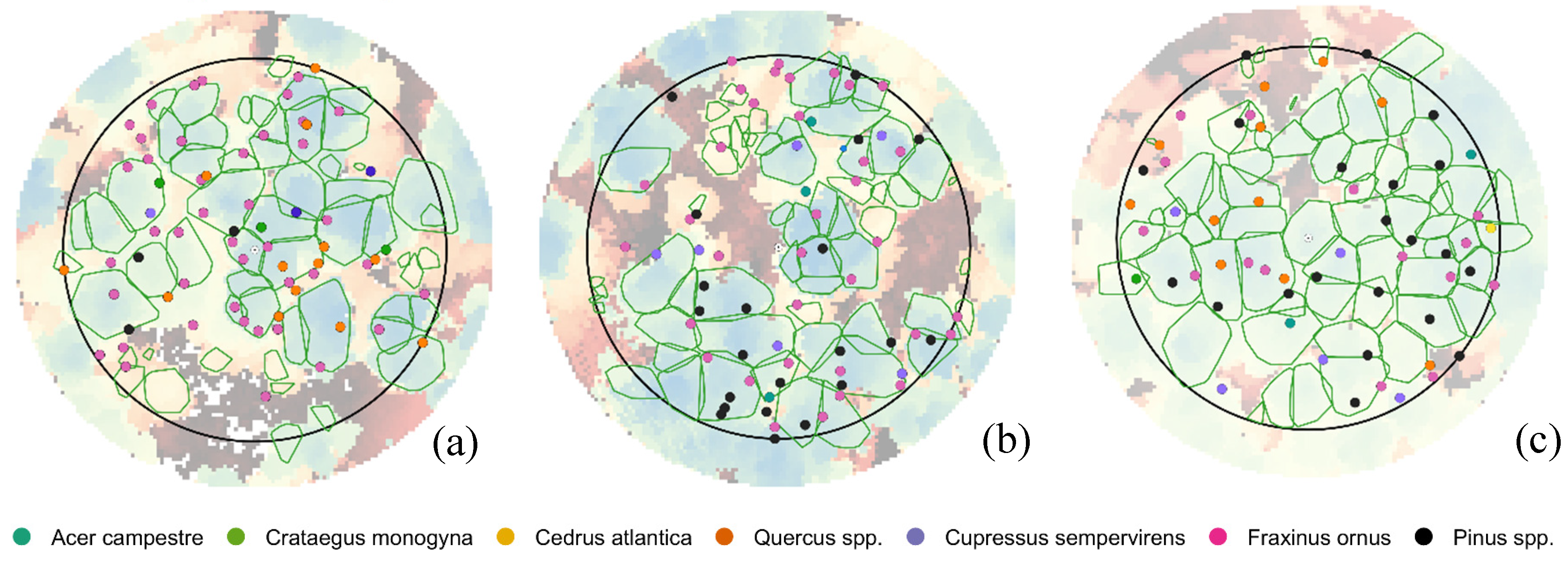
The aim of this study is to assess the capability of the low-cost UAV-LS system developed in [
14] to obtain structural and dendrometric parameters in a complex layered forest. Specifically, ITC were delineated by means of the benchmarked [
45] tree detection methods developed by [
46] and by [
47] on ALS data. The DBH and aboveground biomass (AGB) were estimated from crown area and tree height of segmented trees by allometric equations specific for Nearctic-Temperate mixed forests-Gymnosperm [
48]. The main research questions of this study are: (i) is the performance of ITC segmentation based on UAV-LS comparable to ALS? (ii) which is the impact of ITC algorithm parameters setting on the number of detected trees, DBH, height and aboveground biomass estimates? (iii) is the accuracy of estimations satisfactory for inventory purposes especially in layered complex forest?
4. Discussion
Delineation accuracy of ITC segmentation obtained in this study was in line with other studies based on ALS. Ref. [
55] evaluated the quality, accuracy and feasibility of nine automatic tree extraction methods based on ALS data acquired in boreal forest stands with point densities of 2, 4 and 8 points/m
2. The capabilities of detecting trees resulted between 25% and 102%, while the point density had a minor impact on the segmentation rate. The commission error varied between 0% and 26.5%, while the omission error varied between 35% and 68%. As expected, the taller trees were detected with a better accuracy; the RMSE of height estimation for the delineated trees ranged from 60 to 80 cm for the best methods. Ref. [
45] benchmarked eight ALS tree detection methods, including the method that was used here [
53], across different regions, forest types and structures in the Alps. Considering all the methods, the omission error ranged between 51% and 63%, being higher for multi-layered mixed and coniferous forests and lower for single-layered coniferous forest (37%). The method of [
53] that was used here produced an overall omission error of 61%, while the omission error in single layered mixed forests was 25%, in single layered coniferous forests was 40%, in multi layered mixed forests was 75% and in multi layered coniferous forest was 65%. Ref. [
56] benchmarked five ALS-based individual tree detection methods with a point cloud density of 2, 4 and 8 points/m
2 acquired in five boreal forests with diverse stand conditions and different developmental stages (i.e., from deciduous-dominated to mixed, to coniferous-dominated and from old to mature to very young stands) considering four crown classes, i.e., dominant, codominant, intermediate and suppressed trees. Their study revealed that omission error varied between 25% and 63% and that all methods tended to overestimate the number of dominant trees and underestimate the number of subordinate trees. Delineation of dominated trees was challenging for all methods.
Similar to [
45,
55,
56], one finding of our study was that the omission error varies between 40% and 57% and that the largest fraction of not detected trees was in the understory, which suggests they were dominated trees. This outcome, that needs to be confirmed by further studies considering larger datasets, confirms what [
55] highlighted concerning the effect of point density on the ITC delineation accuracy and retract the outcomes of [
56]: high levels of laser point density do not increase the delineation accuracy. In fact, also using LiDAR data with very high density as in this study (i.e., 193 points/m
2) the accuracy of tree segmentation was similar to that obtained in the studies that benchmarked individual tree detection methods using ALS data with point density ranging from 2 to 8 points/m
2.
The most important experiences in using UAV-borne LiDAR data for ITC delineation are from [
15,
36,
38,
57,
58,
59].
Ref. [
15] used high-resolution LiDAR data captured from a small multirotor UAV to extract individual trees in 6 circular plots in a four-year-old Tasmanian blue gum regular plantation (density ranging from 680 to 1560 trees/ha) located in Southern Tasmania (Australia) using an adaptation of the method outlined by [
47]. By means of this approach, 91% of field-measured trees were correctly matched to the UAV segmented trees across all plots. In their successive study, Ref. [
57], using the same data set, tested five tree detection routines to assess the tree delineation accuracy. The percentage of field-measured trees correctly matched with UAV-LS delineated trees resulted between 92% and 97%. The highest rate of omission occurred in small trees, while commission errors for most algorithms was caused by over-segmentation of large trees. The study also highlighted that improvement in omission rate occurs using higher point densities (~50 points/m
2).
Ref. [
36] delineated trees from UAV-borne laser scanner data acquired over a 64 m × 64 m study area located in Evo, Southern Finland, with a density of about 490 trees/ha. A two steps approach for individual tree detection was used, based on the application of a local maximum filtering algorithm on the CHM and on the application of a watershed algorithm to successively delineate the tree crowns. The average detection rate resulted 84.2%, being 100% for isolated and dominant trees, but the relatively low value of tree density of the study area, facilitating the detection process, should be considered. When utilizing direct measurement in the point cloud, Ref. [
36] obtained a relative RMSE equal to 6.47% in height estimation and 27.46% in DBH estimation.
Ref. [
38] delineated individual tree crows from UAV-LS data acquired in an ecotone area in Northern Arizona (USA) which includes a shrubland-grassland meadow adjacent to a ponderosa pine forest with a density of 220 trees/ha. They obtained a determination coefficient between the number of trees delineated from the LiDAR data and field-based tree density equal to 0.77 and a determination coefficient for tree height within dense canopy cover equal to 0.79, where only the tallest tree canopy heights were successfully estimated and the shorter trees under the tall canopies were missed by the laser scanner.
Ref. [
58] applied a methodology to UAV-LS data based on fitting and modeling the 3D-shape of trees in a hazel grove using RANSAC [
59] obtaining a detection rate equal to 86%.
Ref. [
60] assessed the performance of four algorithms (three based on CHM and one on point cloud) for individual tree detection using UAV-LS data in pure ginkgo planted forest in China with density ranging from 400 to 700 trees per hectare, DBH ranging from 16 cm to 20 cm and Lorey’s height from 12 m to 11 m. The individual tree detection algorithm based on point cloud was the best performing in plot with low density but was the worst as the tree density increased.
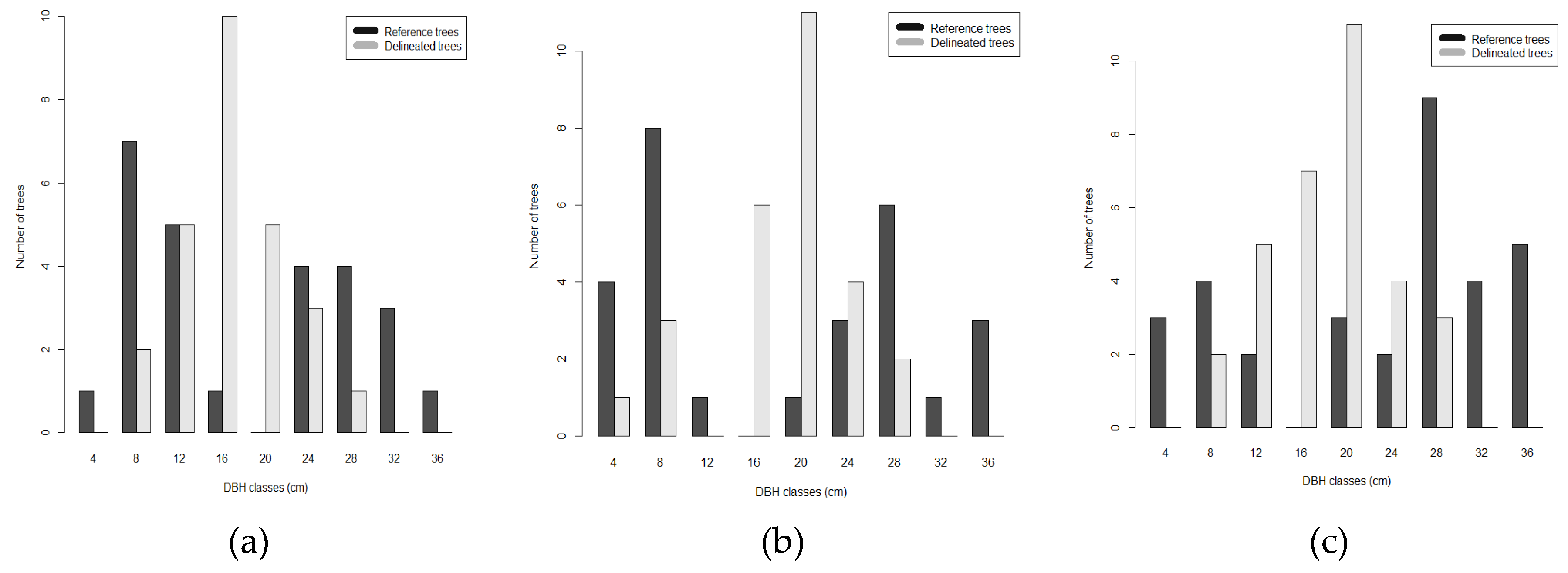
Unlike our study, that was conducted in multi-layer forest stands with a density higher than 1000 trees/ha and with a high level of crown cover, the results of the studies reported above were obtained in isolated trees, in stands composed by only dominated trees, in plantation where trees were planted with a regular pattern, and overall, in stands with a tree density approximately half of that of our analysis. And as a matter of fact, the levels of accuracy obtained in our study were slightly lower. The optimal setting of itcLiDAR() function has determined a detection rate ranging between 40% and 57% in the three plots, while the main source of omission error was the failure to separate two or three medium trees that have similar heights and were located close to each other. The tuning of the ITC algorithm parameters resulted quite important in reaching the highest determination rates that ranged from 23.4% to 40.6% in plot 6.1, 21.2% and 40.9% in plot 6.2 and 32.1% and 57.1% in plot 7.2 across the parameter optimization space. This was an important outcome: knowing the possible range of variability of each parameter was the starting point for the individual tree segmentation process to reach the optimal determination rates. Hence, the application of a parameter tuning procedure is suggested to optimize the segmentation process for a specific set of forest characteristics. Our findings agree with [
44], which reports that a certain degree of calibration is necessary to obtain the best results in tree detection and delineation, where size and shape of the 3D kernel play a crucial role. Another reason that explains the lower values of detection rate obtained here with respect to other studies is the approach used to match the delineated trees with the field surveyed trees. The approach of [
53] considers the inclusion of a field-measured tree inside the delineated crown and difference of height between the field measured tree and the delineated tree. Other methods consider also the planar distance between delineated and reference trees (i.e., [
61]) or the maximum values of height differences (i.e., [
62]). Depending on the method used for tree matching, the results can be quite different. Vertical forest stratification in combination with the matching process were probably the factors that have determined the overestimation of canopy height. Intermediate trees, that occupied a position underneath the dominant and co-dominants trees, were erroneously coupled with the higher trees. Indeed, in some cases crowns of dominant trees, due to the specific shape of species present in the stands, were segmented as two distinct trees, so in this way a delineated tree was coupled with the dominant tree and the other one with the codominant or intermediate tree, leading to an over estimation of tree height and consequently of tree biomass.
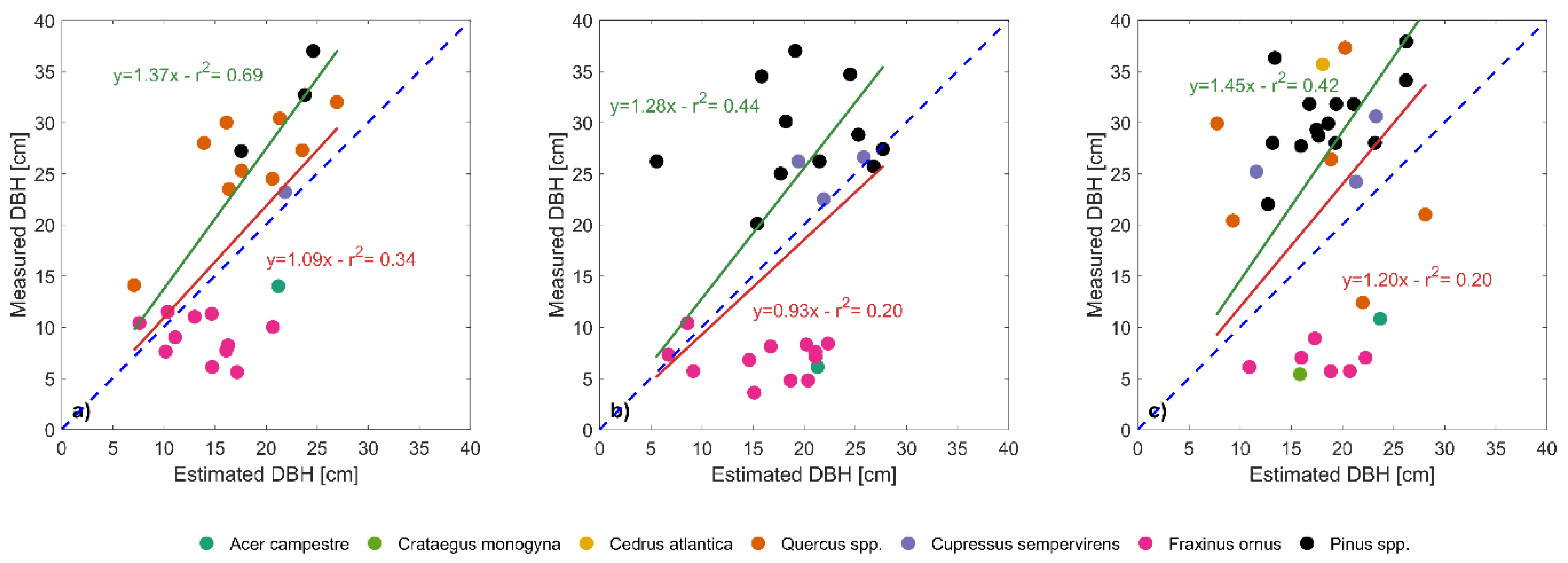
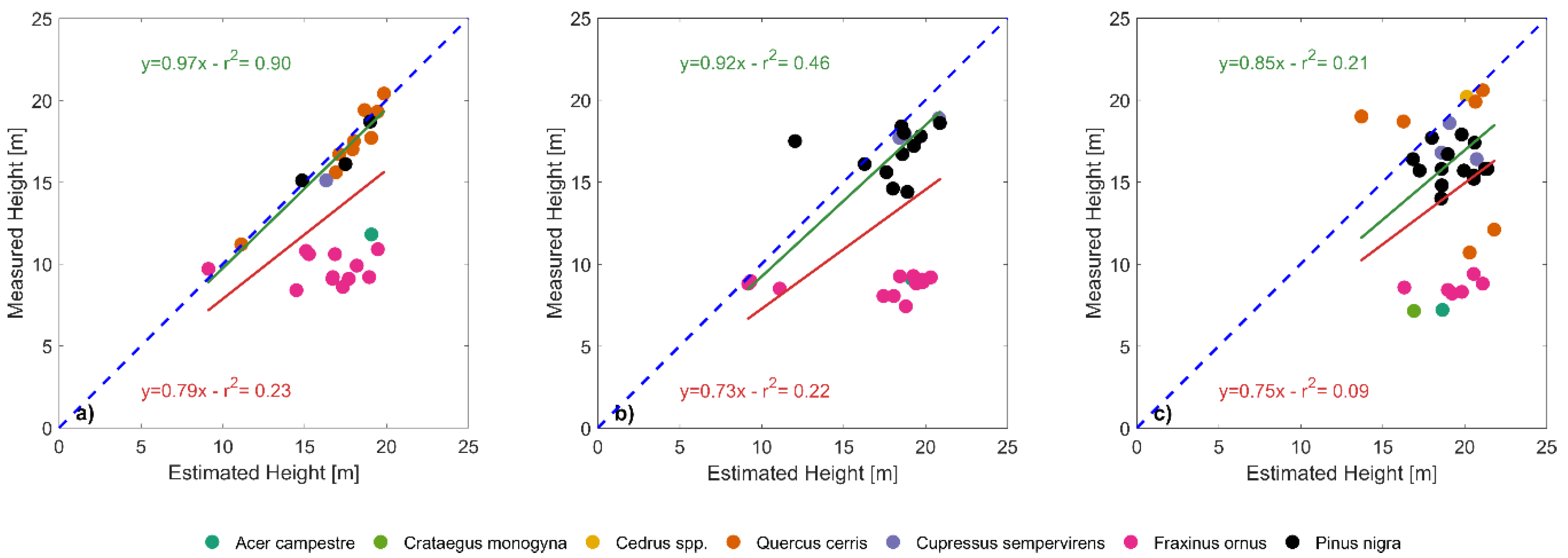
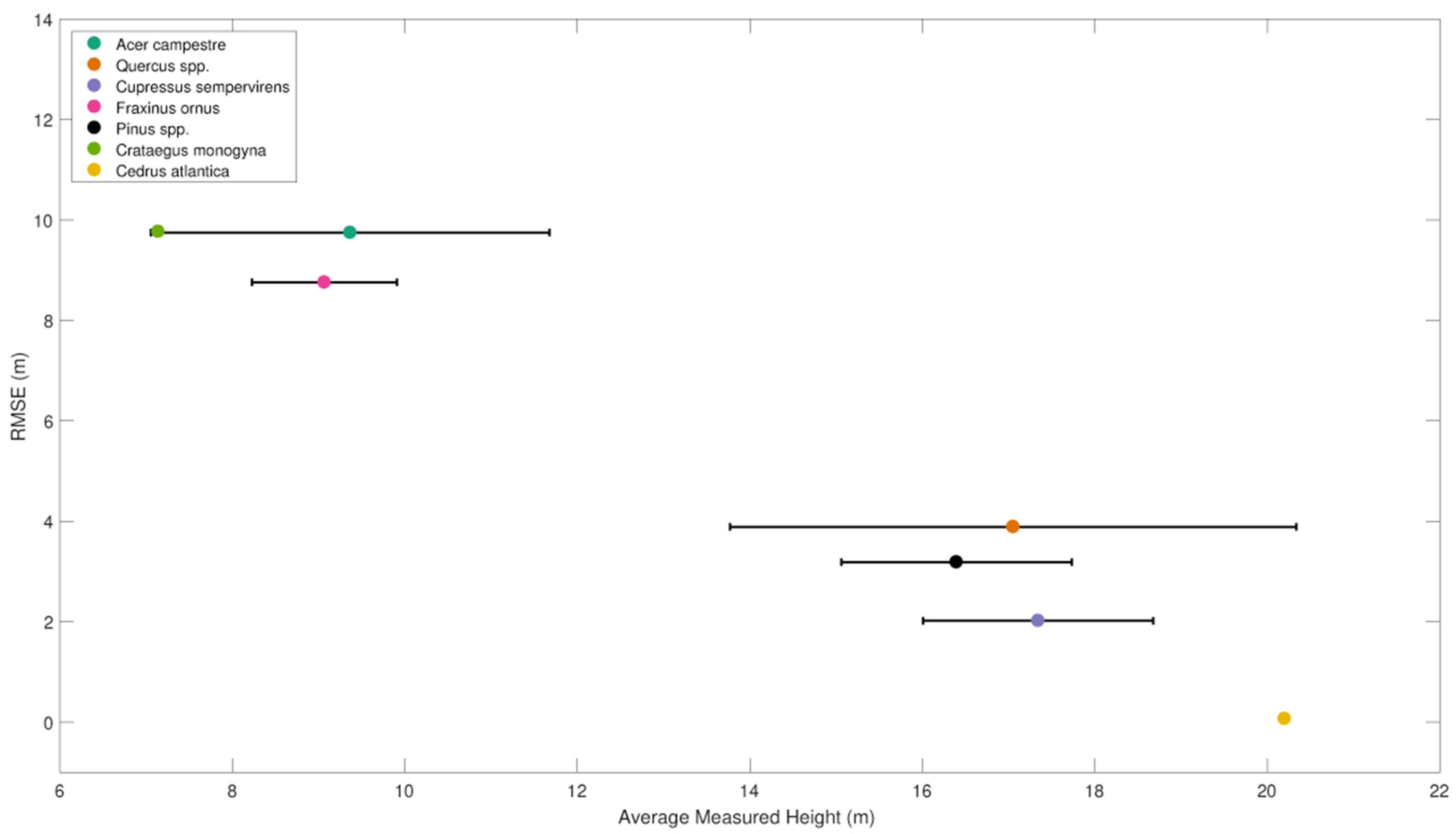
The effect of stratification on the estimation of tree heights was clearly visible when removing shorter trees from the analysis. The coefficient of determination for estimated versus measured tree height, in fact, greatly increased when significantly shorter trees were removed, reaching even higher values than [
38] in plot 6.1 (0.90 vs. 0.79). In fact, when considering individually the single species, the effect of stratification was relevant: taller species that stand out clearly from the dense mixed canopy have lower RMSEs between measured and estimated heights, while shorter species were less easily distinguished and have associated higher errors. We should also consider the error that occur during the ground-based tree height measurements which was related to the tree top shape, determined by the apical dominance: the higher the apical dominance, the greater the ability to detect the tree top in field survey. This implies that in species with a strong apical dominance (e.g., Atlantic cedar and Mediterranean cypress) the uncertainty in tree height field measurement was lower than in species with moderate or low apical dominance (e.g., European black pine and Turkey oak). This aspect reflects in the RMSE that was lower in species with greater apical dominance (
Figure 8).
This study was based on a sample size of 186 trees, which could prevent the upscaling of the results obtained here to larger areas. However, comparable sample sizes were used in several studies focusing on small areas without loss of generality [
58]. Ref. [
43] employed UAV-LS data to build 200 tree models by a quantitative structure approach and compared them with terrestrial laser scanning obtaining reliable volume estimations for trunks and branches ≥ 30 cm. Similarly, Ref. [
44] used multiple segmentation algorithms over about 120 trees, while [
58] performed 3D volume reconstruction with UAV-LS on 181 hazel trees. Overall, these studies increase the confidence in the validity of the approach proposed here, that definitely calls for further and deeper analysis based on forthcoming larger datasets.