Comparing Filtering Techniques for Removing Vegetation from UAV-Based Photogrammetric Point Clouds
Abstract
:1. Introduction
2. Methods
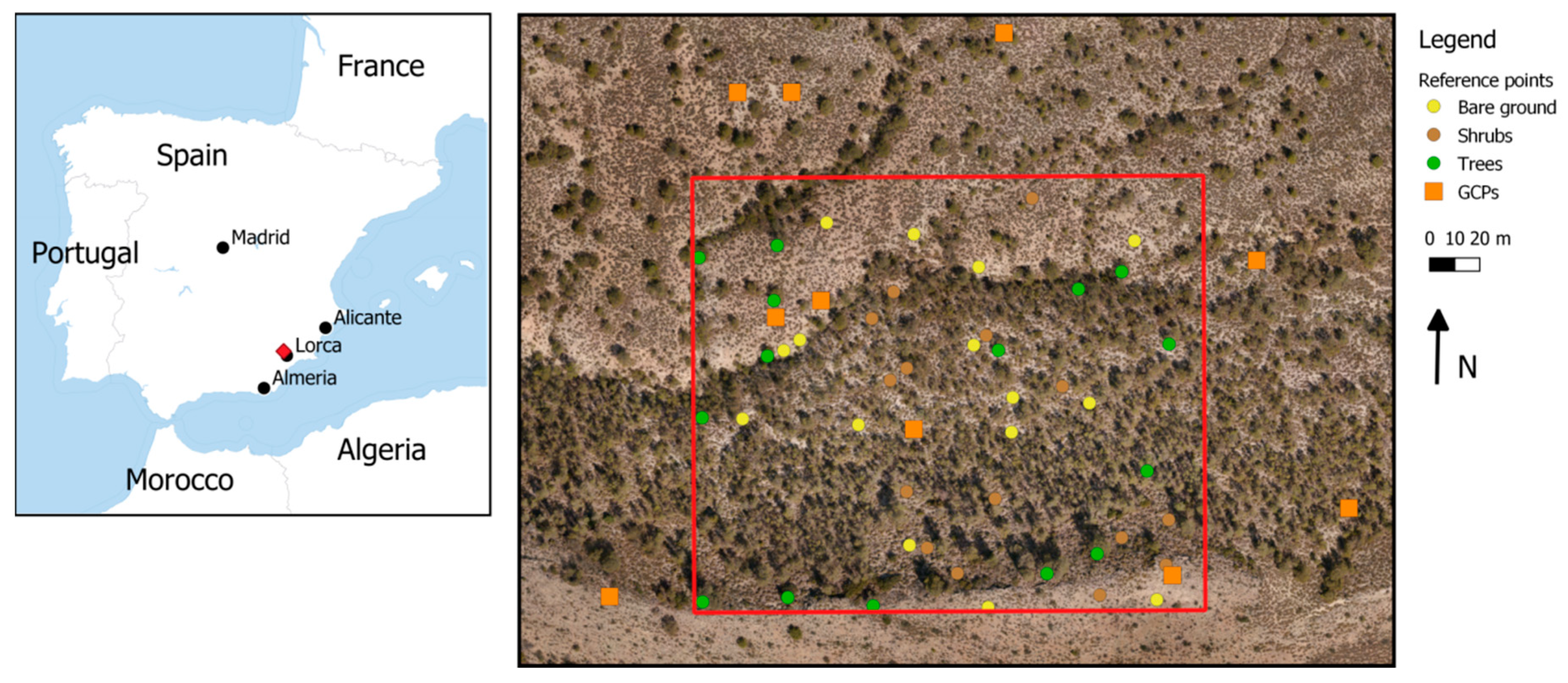
2.1. Study Area
2.2. Unmanned Aerial Vehicle, Camera and Photo Processing
2.3. Filter Algorithms and Point Cloud Interpolation
- Ground point classification based on a vegetation index (VI), particularly the excessive greenness as calculated from the RGB color values
- Photoscan native filtering algorithm (PS) [18]
- Iterative surface lowering (ISL) which resembles the algorithm described by [11]
- A combination of ISL and VI (ISL_VI).
2.3.1. Filtering based on Excessive Greenness Index
2.3.2. TIN Densification
2.3.3. Agisoft Photoscan Native Filtering Algorithm
2.3.4. Iterative Surface Lowering (ISL)
2.3.5. ISL + VI
2.3.6. Output
- DSM: average elevation of all points inside grid cell boundaries
- DTM: average elevation of all ground points inside grid cell boundaries
- VI: average ExG values of all points inside grid cell boundaries
- VIground: average ExG values of all ground points inside grid cell boundaries
- Image mosaic: average color values of all points within grid cell boundaries
2.4. Error Assessment of Resulting DTMs
2.4.1. Quantitative Error Assessment
2.4.2. Qualitative Error Assessment
3. Results
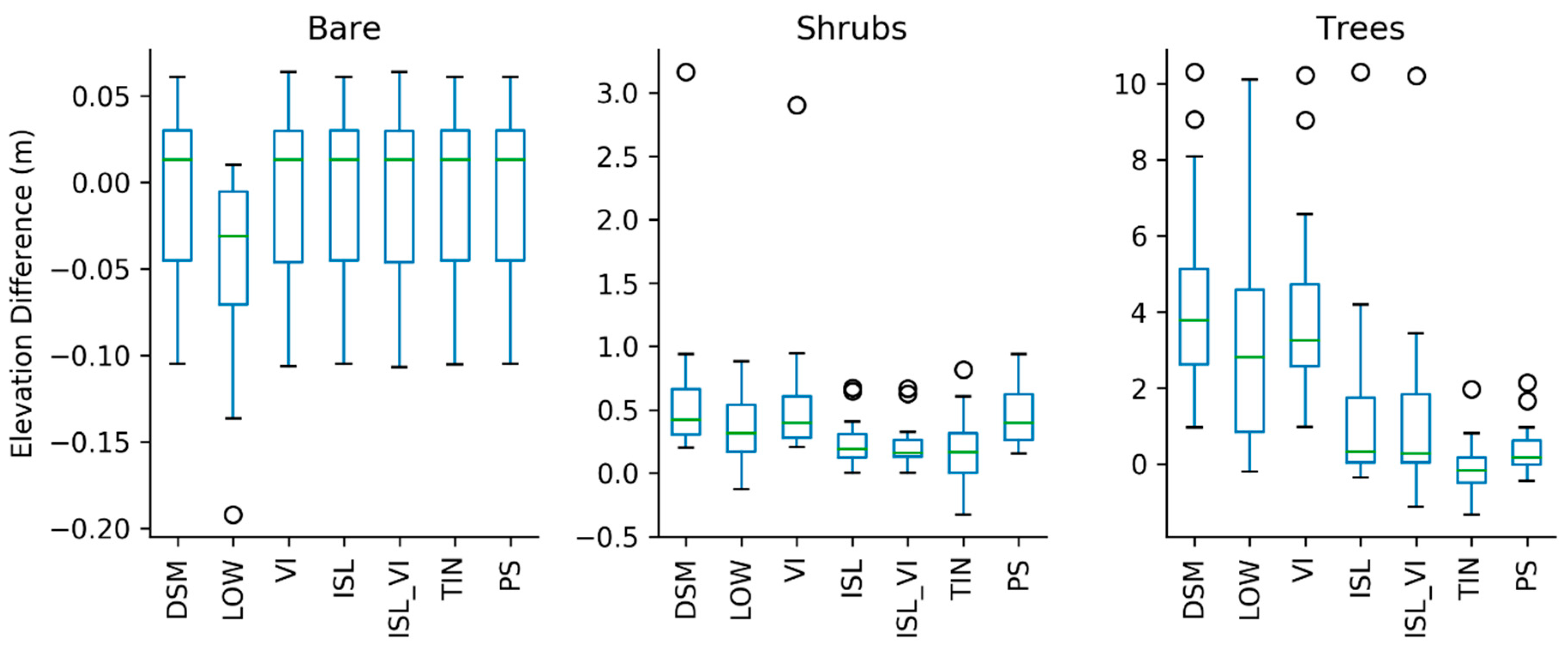
3.1. Quantitative Comparison of Filter Methods
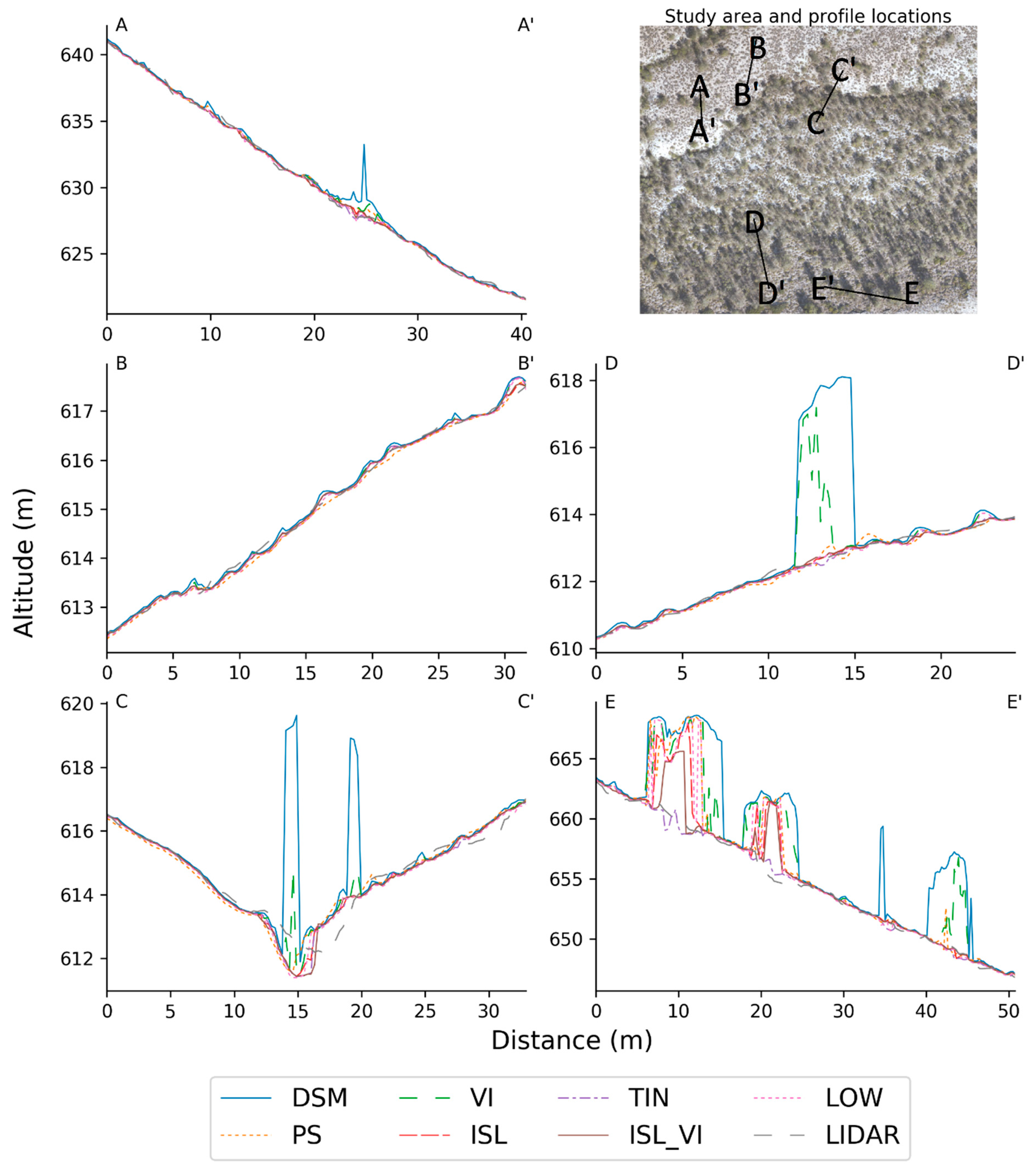
3.2. Qualitative Comparison of Filter Methods
4. Discussion
4.1. Performance of Filter Methods
4.2. Comparison of Filters to Previous Studies
4.3. Further Improvement of Filtering Methods
4.4. Which Filter Should Be Used? Implications for Environmental Modelling
5. Conclusions
- To assess the best algorithm for filtering vegetation from a Digital Surface Model five methods for filtering vegetation from SfM point clouds were tested in an area in SE Spain with a Mediterranean climate. This area represents a combination of bare areas, shrubland areas and forested areas, which ensured proper testing of all involved algorithms.
- Results showed that for bare ground areas there was little to no difference between the filtering methods, which is to be expected because there is little to no vegetation present to filter. For shrub areas and tree areas, the ISL_VI and TIN method performed best.
- These results show that the off-the-shelf algorithms are not always the best way to remove unwanted vegetation from a point cloud, but instead custom algorithms such as TIN densification should be used to obtain a vegetation-less DTM.
- Choosing the right filtering technique for hydrological and sediment transport modelling is essential to obtaining correct modelling outputs. Mistakes in the input DTM may change the modelled connectivity of the landscape, which in turn influences calculations of water and sediment yields.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Squires, J.R.; DeCesare, N.J.; Olson, L.E.; Kolbe, J.A.; Hebblewhite, M.; Parks, S.A. Combining resource selection and movement behavior to predict corridors for Canada lynx at their southern range periphery. Biol. Conserv. 2013, 157, 187–195. [Google Scholar] [CrossRef]
- Anders, N.S.; Seijmonsbergen, A.C.; Bouten, W. Geomorphological Change Detection Using Object-Based Feature Extraction From Multi-Temporal LiDAR Data. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1587–1591. [Google Scholar] [CrossRef] [Green Version]
- Sofia, G.; Hillier, J.K.; Conway, S.J. Frontiers in Geomorphometry and Earth Surface Dynamics: Possibilities, limitations and perspectives. Earth Surf. Dyn. 2016, 4, 721–725. [Google Scholar] [CrossRef]
- Masselink, R.J.H.; Heckmann, T.; Temme, A.J.A.M.; Anders, N.S.; Gooren, H.P.A.; Keesstra, S.D. A network theory approach for a better understanding of overland flow connectivity. Hydrol. Process. 2017, 31, 207–220. [Google Scholar] [CrossRef]
- Pandey, A.; Himanshu, S.K.; Mishra, S.K.; Singh, V.P. Physically based soil erosion and sediment yield models revisited. Catena 2016, 147, 595–620. [Google Scholar] [CrossRef]
- Liu, X. Airborne LiDAR for DEM generation: Some critical issues. Prog. Phys. Geogr. 2008, 32, 31–49. [Google Scholar]
- Eitel, J.U.; Magney, T.S.; Vierling, L.A.; Brown, T.T.; Huggins, D.R. LiDAR based biomass and crop nitrogen estimates for rapid, non-destructive assessment of wheat nitrogen status. Field Crop. Res. 2014, 159, 21–32. [Google Scholar] [CrossRef]
- Turner, D.; Lucieer, A.; Watson, C. An automated technique for generation georectified mosaics from ultra-high resolution Unmanned Aerial Vehicle (UAV) imagery, based on structure from motion (SfM) point clouds. Remote Sens. 2012, 4, 1392–1410. [Google Scholar] [CrossRef]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. ‘Structure-from-Motion’ photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef]
- Sithole, G.; Vosselman, G. Experimental comparison of filter algorithms for bare-Earth extraction from airborne laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2004, 59, 85–101. [Google Scholar] [CrossRef]
- Kraus, K.; Pfeifer, N. Determination of terrain models in wooded areas with airborne laser scanner data. ISPRS J. Photogramm. Remote Sens. 1998, 53, 193–203. [Google Scholar] [CrossRef]
- Kraus, K.; Otepka, J. DTM Modelling and Visualization-the SCOP Approach; Photogrammetric Week 05; Fritsch, D., Ed.; Wichmann Verlag: Heidelberg/Berlin, Germany, 2005; pp. 241–252. [Google Scholar]
- Isenburg, M. “Efficient LiDAR Processing Software” (Version 170511, Academic). Available online: http://rapidlasso.com/LAStools (accessed on 1 August 2014).
- Axelsson, P. Processing of laser scanner data—Algorithms and applications. ISPRS J. Photogramm. Remote Sens. 1999, 54, 138–147. [Google Scholar] [CrossRef]
- Axelsson, P. DEM generation from laser scanner data using adaptive TIN models. Int. Arch. Photogramm. Remote Sens. 2000, 33, 111–118. [Google Scholar]
- Poli, D.; Soille, P. Digital Surface Model Extraction and Refinement through Image Segmentation – Application to the ISPRS Benchmark Stereo Dataset. Photogrammetrie Fernerkundung Geoinf. 2012, 317–329. [Google Scholar] [CrossRef]
- AgiSoft LLC. Agisoft PhotoScan User Manual, Professional Edition, Version 1.4; AgiSoft LLC: St. Petersburg, Russia, 2018. [Google Scholar]
- Nadal-Romero, E.; Revuelto, J.; Errea, P.; López-Moreno, J. The application of terrestrial laser scanner and SfM photogrammetry in measuring erosion and deposition processes in two opposite slopes in a humid badlands area (central Spanish Pyrenees). SOIL 2015, 1, 561–573. [Google Scholar] [CrossRef] [Green Version]
- Jensen, J.; Mathews, A. Assessment of Image-Based Point Cloud Products to Generate a Bare Earth Surface and Estimate Canopy Heights in a Woodland Ecosystem. Remote Sens. 2016, 8, 50. [Google Scholar] [CrossRef]
- Becker, C.; Häni, N.; Rosinskaya, E.; d’Angelo, E.; Strecha, C. Classification of aerial photogrammetric 3D point clouds. In Proceedings of the ISPRS Hannover Workshop: HRIGI 17 – CMRT 17 – ISA 17 – EuroCOW 17, Hannover, Germany, 6–9 June 2017. [Google Scholar]
- Serifoglu Yilmaz, C.; Gungor, O. Comparison of the performances of ground filtering algorithms and DTM generation from a UAV-based point cloud. Geocarto Int. 2016, 1–16. [Google Scholar] [CrossRef]
- Rodriguez-Lloveras, X.; Bussi, G.; Francés, F.; Rodriguez-Caballero, E.; Solé-Benet, A.; Calle, M.; Benito, G. Patterns of runoff and sediment production in response to land-use changes in an ungauged Mediterranean catchment. J. Hydrol. 2015, 531, 1054–1066. [Google Scholar] [CrossRef]
- Alías-Pérez, J. Project LUCDEME: Proyecto LUCDEME: Mapa de Suelos de Lorca-953 (Soil Map of Lorca-953, scale 1:100,000); ICONA, Universidad de Murcia, Ministerio de Agricultura Pesca y Alimentación: Madrid, Spain, 1988. (In Spanish) [Google Scholar]
- López Bermúdez, F.; Albaladejo, J. Factores ambientales de la degradacion del suelo en el area mediterranea (Environmental factors of soil degradation in a Mediterranean area). In Degradacion y Regeneracion del Suelo en Condiciones Ambientales Mediterraneas (Soil Degradation and Rehabilitation in Mediterranean Environmental Conditions); Albaladejo, J., Stocking, M.A., Díaz, E., Eds.; CSIC: Murcia, Spain, 1990; pp. 15–45. (In Spanish) [Google Scholar]
- Pérez, A.; Martín, J.M.; Pérez, T.; Torres, M.; Fernández, A.; Burgos, R.; Madrona, M.T.; Valle, F.; Díaz, J.L. Project LUCDEME: Proyecto LUCDEME: Mapa de Suelos de Velez Blanco-952 (Soil Map of Velez Blanco-952, scale 1:100,000); ICONA, Universidad de Murcia, Ministerio de Agricultura Pesca y Alimentación: Madrid, Spain, 1993. (In Spanish) [Google Scholar]
- Rojo Serrano, L. Spanish national plan to combat desertification. In Desertification in a European Context: Physical and Socio-Economic Aspects. Luxembourg, Report EUR 15414 EN; Office for Official Publications of the European Communities: Luxembourg, 1995; pp. 357–358. [Google Scholar]
- Anders, N.S.; Masselink, R.; Keesstra, S.D.; Suomalainen, J. High-res digital surface modeling using fixed-wing UAV-based photogrammetry. In Proceedings of the Geomorphometry 2013, Nanjing, China, 16–20 October 2013; pp. 16–20. [Google Scholar]
- Meng, X.; Currit, N.; Zhao, K. Ground Filtering Algorithms for Airborne LiDAR Data: A Review of Critical Issues. Remote Sens. 2010, 2, 833–860. [Google Scholar] [CrossRef] [Green Version]
- Wallace, L.; Lucieer, A.; Malenovský, Z.; Turner, D.; Vopěnka, P. Assessment of Forest Structure Using Two UAV Techniques: A Comparison of Airborne Laser Scanning and Structure from Motion (SfM) Point Clouds. Forests 2016, 7, 62. [Google Scholar] [CrossRef]
- Yilmaz, V.; Konakoglu, B.; Serifoglu, C.; Gungor, O.; Gökalp, E. Image classification-based ground filtering of point clouds extracted from UAV-based aerial photos. Geocarto Int. 2016, 1–11. [Google Scholar] [CrossRef]
- Ponti, M.P. Segmentation of Low-Cost Remote Sensing Images Combining Vegetation Indices and Mean Shift. Geosci. Remote Sens. Lett. 2013, 10, 67–70. [Google Scholar] [CrossRef]
- Zhao, X.; Guo, Q.; Su, Y.; Xue, B. Improved progressive TIN densification filtering algorithm for airborne LiDAR data in forested areas. ISPRS J. Photogramm. Remote Sens. 2016, 117, 79–91. [Google Scholar] [CrossRef] [Green Version]
- PNOA. Plan Nacional de Ortofotografía Aérea. 2014. Data downloaded via Centro de Descargas of the Instituto Geografica Nacional. Available online: http://centrodedescargas.cnig.es/ (accessed on 2 August 2014).
- Fraser, R.H.; Olthof, I.; Lantz, T.C.; Schmitt, C. UAV photogrammetry for mapping vegetation in the low-Arctic. Arct. Sci. 2016, 2, 79–102. [Google Scholar] [CrossRef] [Green Version]
- Aguilar, F.J.; Mills, J.P.; Delgado, J.; Aguilar, M.A.; Negreiros, J.G.; Pérez, J.L. Modelling vertical error in LiDAR-derived digital elevation models. ISPRS J. Photogramm. Remote Sens. 2010, 65, 103–110. [Google Scholar] [CrossRef]
- Keesstra, S.; Nunes, J.P.; Saco, P.; Parsons, T.; Poeppl, R.; Masselink, R.; Cerdá, A. The way forward: Can connectivity be useful to design better measuring and modelling schemes for water and sediment dynamics? Sci. Total Environ. 2018, 644, 1557–1572. [Google Scholar] [CrossRef] [PubMed]
- Nunes, J.P.; Wainwright, J.; Bielders, C.L.; Darboux, F.; Fiener, P.; Finger, D.; Turnbull, L. Better models are more effectively connected models. Earth Surf. Process. Landforms 2018, 43, 1355–1360. [Google Scholar] [CrossRef]

| Ground | Vegetation | % Filtered | Bare | Shrub | Tree | |
|---|---|---|---|---|---|---|
| DSM | 3.20 × 107 | 0 | 0.00 | 0.05 | 0.96 | 5.16 |
| ISL | 2.40 × 107 | 0.79 × 107 | 24.83 | 0.05 | 0.31 | 3.04 |
| ISL_VI | 1.40 × 107 | 1.79 × 107 | 56.18 | 0.05 | 0.29 | 2.94 |
| LOW | 3.20 × 107 | 0 | 0.00 | 0.08 | 0.44 | 4.47 |
| PS | 3.00 × 107 | 0.19 × 107 | 6.06 | 0.05 | 0.50 | 0.81 |
| TIN | 2.07 × 107 | 1.13 × 107 | 35.41 | 0.05 | 0.33 | 0.78 |
| VI | 1.70 × 107 | 1.50 × 107 | 46.80 | 0.05 | 0.89 | 4.89 |
| DSM | ISL | ISL_VI | LOW | PS | TIN | ||
|---|---|---|---|---|---|---|---|
| DSM | Bare p = 0.99 | ||||||
| ISL | 0 | ||||||
| ISL_VI | 0 | 0 | |||||
| LOW | 0.009 | 0.01 | 0.009 | ||||
| PS | 0 | 0 | 0 | −0.009 | |||
| TIN | 0 | 0 | 0 | −0.009 | 0 | ||
| VI | 0 | 0 | 0 | −0.009 | 0 | 0 | |
| DSM | Shrubs p = 0.017 | ||||||
| ISL | −0.4074 | ||||||
| ISL_VI | −0.4259 | −0.0185 | |||||
| LOW | −0.2873 | 0.1201 | 0.1387 | ||||
| PS | −0.2008 | 0.2066 | 0.2251 | 0.0865 | |||
| TIN | −0.4038 | 0.0036 | 0.0221 | −0.1165 | −0.203 | ||
| VI | −0.0417 | 0.3657 | 0.3842 | 0.2456 | 0.1591 | 0.3621 | |
| DSM | Trees p < 0.001 | ||||||
| ISL | −2.8992 | ||||||
| ISL_VI | −2.9337 | −0.0346 | |||||
| LOW | −1.025 | 1.8742 | 1.9087 | ||||
| PS | −3.8948 | −0.9956 | −0.961 | −2.8698 | |||
| TIN | −3.8393 | −0.9402 | −0.9056 | −2.8143 | 0.0554 | ||
| VI | −0.2577 | 2.6415 | 2.676 | 0.7673 | 3.6371 | 3.5816 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anders, N.; Valente, J.; Masselink, R.; Keesstra, S. Comparing Filtering Techniques for Removing Vegetation from UAV-Based Photogrammetric Point Clouds. Drones 2019, 3, 61. https://doi.org/10.3390/drones3030061
Anders N, Valente J, Masselink R, Keesstra S. Comparing Filtering Techniques for Removing Vegetation from UAV-Based Photogrammetric Point Clouds. Drones. 2019; 3(3):61. https://doi.org/10.3390/drones3030061
Chicago/Turabian StyleAnders, Niels, João Valente, Rens Masselink, and Saskia Keesstra. 2019. "Comparing Filtering Techniques for Removing Vegetation from UAV-Based Photogrammetric Point Clouds" Drones 3, no. 3: 61. https://doi.org/10.3390/drones3030061
APA StyleAnders, N., Valente, J., Masselink, R., & Keesstra, S. (2019). Comparing Filtering Techniques for Removing Vegetation from UAV-Based Photogrammetric Point Clouds. Drones, 3(3), 61. https://doi.org/10.3390/drones3030061







