Positional Precision Analysis of Orthomosaics Derived from Drone Captured Aerial Imagery
Abstract
1. Introduction
2. Materials and Methods
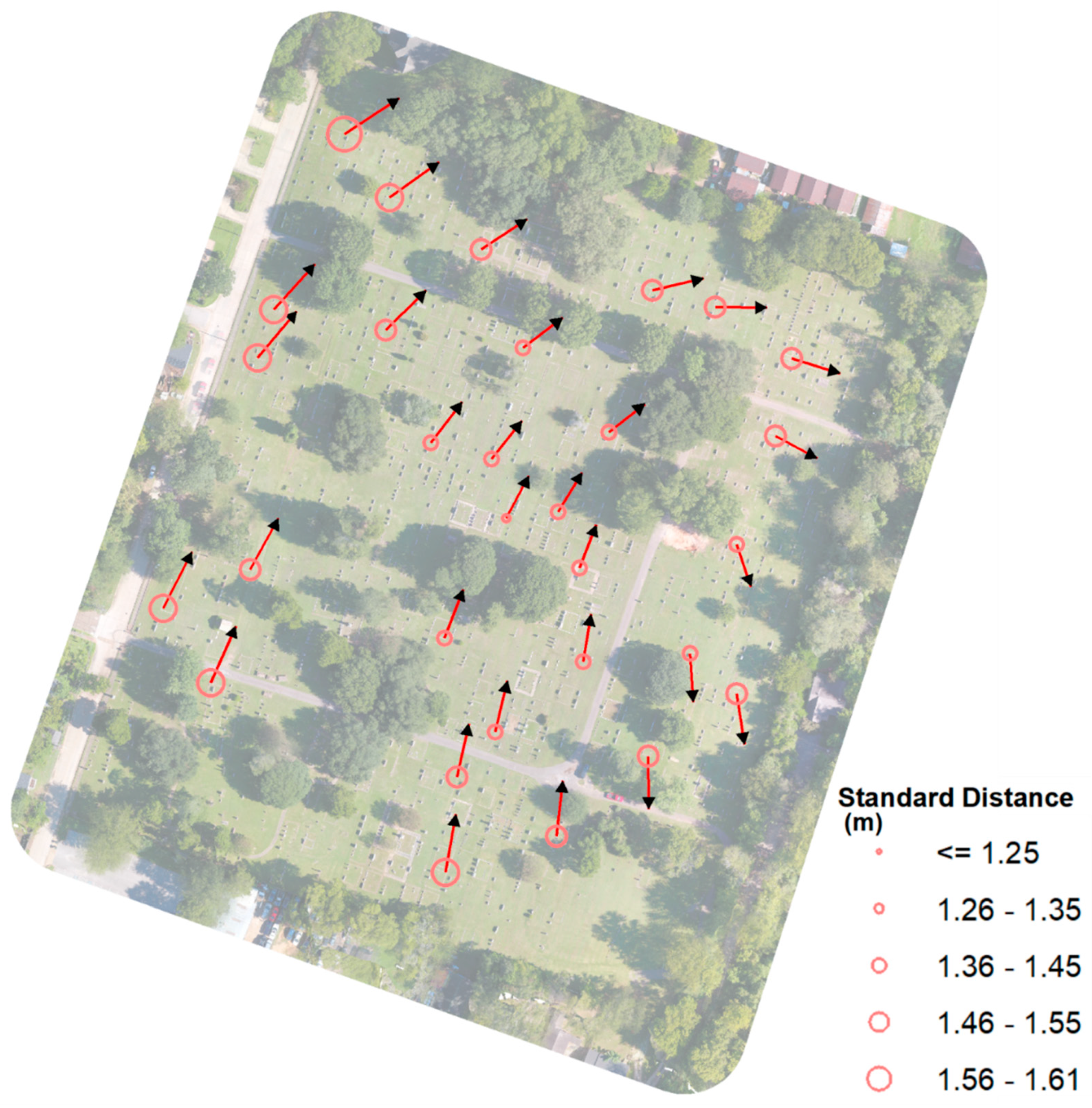
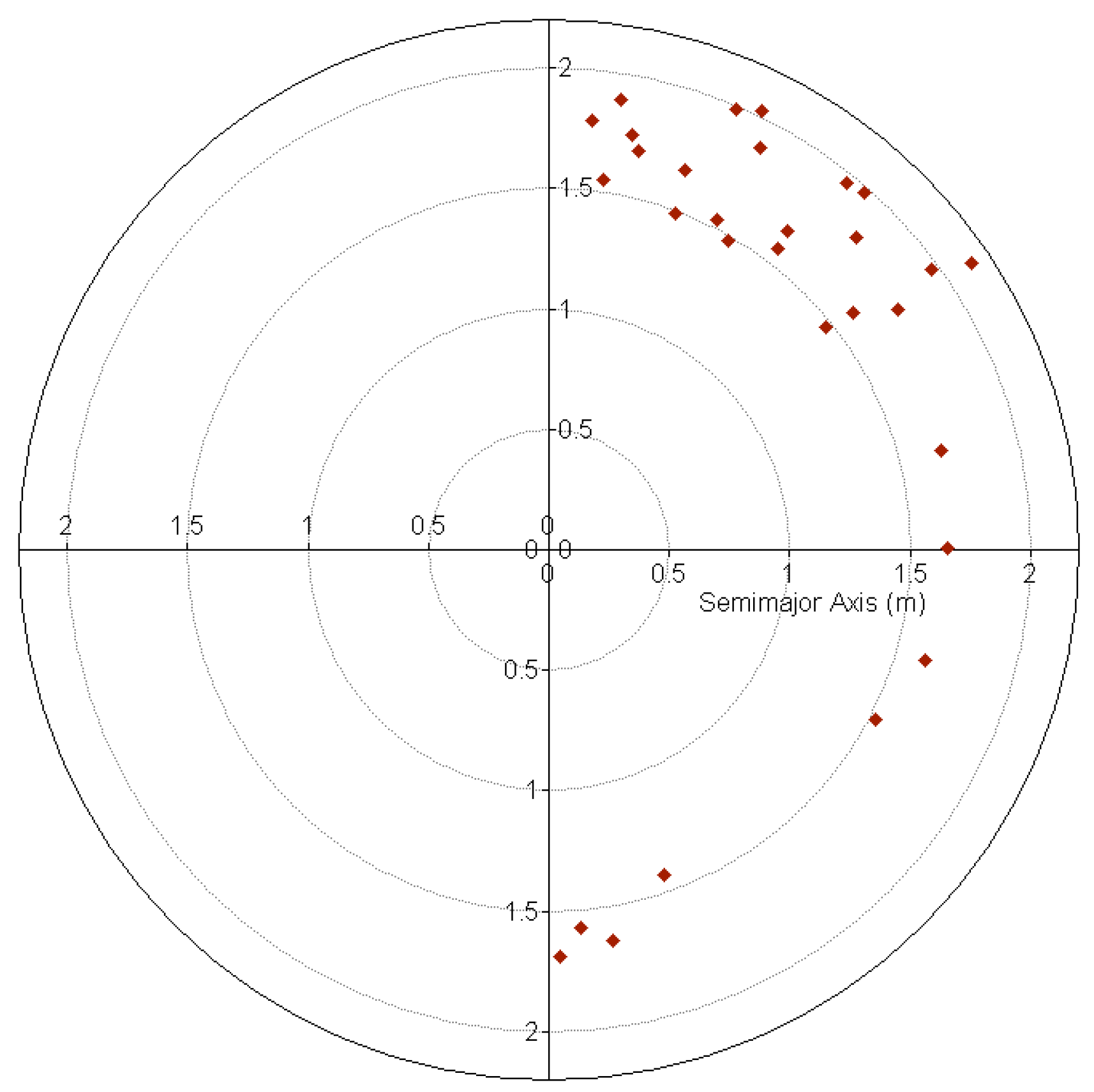
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| GCP ID | X Coordinate of Mean Center (m) | Y Coordinate of Mean Center (m) | Standard Distance of Summary Circle (m) | Azimuth of Ellipse Rotation (degree) | Major Semi-axis of Ellipse (m) | Minor Semi-axis of Ellipse (m) | Area of Deviational Ellipse (sq m) |
|---|---|---|---|---|---|---|---|
| 1 | 343,565.68 | 3,497,810.96 | 1.61 | 55.87 | 2.12 | 0.83 | 5.50 |
| 2 | 343,676.42 | 3,497,644.76 | 1.34 | 175.20 | 1.57 | 1.04 | 5.16 |
| 3 | 343,580.11 | 3,497,790.65 | 1.51 | 53.83 | 1.97 | 0.81 | 5.03 |
| 4 | 343,609.61 | 3,497,774.07 | 1.40 | 55.51 | 1.76 | 0.92 | 5.07 |
| 5 | 343,664.44 | 3,497,760.95 | 1.42 | 75.93 | 1.68 | 1.11 | 5.84 |
| 6 | 343,684.57 | 3,497,755.69 | 1.43 | 89.75 | 1.65 | 1.17 | 6.08 |
| 7 | 343,709.08 | 3,497,739.19 | 1.44 | 106.33 | 1.63 | 1.22 | 6.24 |
| 8 | 343,543.03 | 3,497,754.76 | 1.49 | 41.41 | 1.98 | 0.74 | 4.57 |
| 9 | 343,578.99 | 3,497,748.25 | 1.40 | 44.47 | 1.82 | 0.78 | 4.48 |
| 10 | 343,622.92 | 3,497,742.58 | 1.33 | 52.03 | 1.60 | 0.99 | 4.99 |
| 11 | 343,650.46 | 3,497,715.59 | 1.31 | 51.15 | 1.47 | 1.13 | 5.25 |
| 12 | 343,703.78 | 3,497,714.32 | 1.40 | 117.54 | 1.53 | 1.26 | 6.05 |
| 13 | 343,691.44 | 3,497,679.65 | 1.33 | 160.45 | 1.43 | 1.21 | 5.45 |
| 14 | 343,612.96 | 3,497,706.88 | 1.29 | 37.25 | 1.57 | 0.93 | 4.57 |
| 15 | 343,642.22 | 3,497,641.95 | 1.29 | 8.35 | 1.55 | 0.95 | 4.63 |
| 16 | 343,601.89 | 3,497,605.10 | 1.37 | 11.42 | 1.75 | 0.83 | 4.60 |
| 17 | 343,537.89 | 3,497,739.31 | 1.48 | 39.11 | 1.96 | 0.71 | 4.35 |
| 18 | 343,593.37 | 3,497,712.18 | 1.31 | 36.76 | 1.65 | 0.82 | 4.27 |
| 19 | 343,617.63 | 3,497,687.93 | 1.25 | 26.93 | 1.54 | 0.89 | 4.29 |
| 20 | 343,634.19 | 3,497,689.96 | 1.28 | 30.23 | 1.48 | 1.04 | 4.82 |
| 21 | 343,641.02 | 3,497,672.01 | 1.27 | 20.54 | 1.49 | 1.00 | 4.69 |
| 22 | 343,691.46 | 3,497,631.79 | 1.41 | 170.69 | 1.65 | 1.12 | 5.79 |
| 23 | 343,663.07 | 3,497,611.75 | 1.38 | 178.48 | 1.69 | 0.98 | 5.23 |
| 24 | 343,614.02 | 3,497,619.44 | 1.34 | 12.66 | 1.70 | 0.86 | 4.56 |
| 25 | 343,597.85 | 3,497,649.51 | 1.31 | 19.77 | 1.67 | 0.78 | 4.10 |
| 26 | 343,535.58 | 3,497,671.47 | 1.43 | 27.69 | 1.88 | 0.75 | 4.43 |
| 27 | 343,507.68 | 3,497,659.14 | 1.54 | 25.95 | 2.03 | 0.81 | 5.15 |
| 28 | 343,522.87 | 3,497,635.29 | 1.51 | 23.01 | 1.99 | 0.80 | 4.98 |
| 29 | 343,598.13 | 3,497,574.59 | 1.48 | 9.18 | 1.89 | 0.90 | 5.34 |
| 30 | 343,633.66 | 3,497,586.16 | 1.42 | 5.81 | 1.79 | 0.90 | 5.05 |
References
- Campbell, J.B.; Wynne, R.H. Introduction to Remote Sensing, 5th ed.; Guilford Press: New York, NY, USA, 2011; ISBN 978-1-60918-176-5. [Google Scholar]
- Nex, F.; Remondino, F. UAV for 3D mapping applications: A review. Appl. Geomat. 2014, 6, 1–15. [Google Scholar] [CrossRef]
- Neitzel, F.; Klonowski, J. Mobile 3D mapping with a low-cost UAV system. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, XXXVIII-1-C22, 39–44. [Google Scholar] [CrossRef]
- Viegut, R.; Kulhavy, D.L.; Unger, D.R.; Hung, I.-K.; Humphreys, B. Integrating unmanned aircraft systems to measure linear and areal features into undergraduate forestry education. Int. J. High. Educ. 2018, 7, 63–75. [Google Scholar] [CrossRef]
- Nogueira, F.; da, C.; Roberto, L.; Körting, T.S.; Shiguemori, E.H. Accuracy analysis of orthomosaic and DSM produced from sensor aboard UAV. In Proceedings of the Anias do XVIII Simposio Brasileiro de Sensoriamento Remoto, Santos, Brazil, 28–31 May 2017; pp. 5515–5520. [Google Scholar]
- Kulhavy, D.L.; Endsley, G.; Unger, D.; Grisham, R.; Gannon, M.; Coble, D. Service learning for the Port Jefferson History and Nature Center: Senior capstone forestry course. J. Community Engagem. High. Educ. 2017, 9, 41–53. [Google Scholar]
- Unger, D.; Hung, I.-K.; Zhang, Y.; Kulhavy, D. Integrating drone technology with GPS data collection to enhance forestry students interactive hands-on field experiences. High. Educ. Stud. 2018, 8, 49–62. [Google Scholar] [CrossRef]
- Fardusi, M.; Chianucci, F.; Barbati, A. Concept to practice of geospatial-information tools to assist forest management and planning under precision forestry framework: A review. Ann. Silvic. Res. 2017, 41, 3–14. [Google Scholar]
- Toth, C.; Jóźków, G. Remote sensing platforms and sensors: A survey. ISPRS J. Photogramm. Remote Sens. 2016, 115, 22–36. [Google Scholar] [CrossRef]
- Unger, D.; Kulhavy, D.; Busch-Petersen, K.; Hung, I.-K. Integrating faculty led service learning training to quantify height of natural resources from a spatial science perspective. Int. J. High. Educ. 2016, 5, 104–116. [Google Scholar] [CrossRef][Green Version]
- Zhang, J.; Hu, J.; Lian, J.; Fan, Z.; Ouyang, X.; Ye, W. Seeing the forest from drones: Testing the potential of lightweight drones as a tool for long-term forest monitoring. Biol. Conserv. 2016, 198, 60–69. [Google Scholar] [CrossRef]
- Anderson, K.; Gaston, K. Lightweight unmanned aerial vehicles will revolutionize spatial ecology. Front. Ecol. Environ. 2013, 11, 138–146. [Google Scholar] [CrossRef]
- Paneque-Gálvez, J.; McCall, M.K.; Napoletano, B.M.; Wich, S.A.; Koh, L.P. Small drones for community-based forest monitoring: an assessment of their feasibility and potential in tropical areas. Forests 2014, 5, 1481–1507. [Google Scholar] [CrossRef]
- Liba, N.; Berg-Jürgens, J. Accuracy of orthomosaic enerated by different methods in example of UAV platform MUST Q. IOP Conf. Ser. Mater. Sci. Eng. 2015, 96, 1–8. [Google Scholar] [CrossRef]
- Nagendran, S.K.; Tung, W.Y.; Ismail, M.A.M. Accuracy assessment on low altitude UAV-borne photogrammetry outputs influenced by ground control point at different altitude. IOP Conf. Ser. Earth Environ. Sci. 2018, 169, 1–9. [Google Scholar] [CrossRef]
- Lima, S.; Kux, H.; Shiguemori, E. Accuracy of autonomy navigation of unmanned aircraft systems through imagery. Int. J. Mech. Mechatron. Eng. 2018, 12, 466–470. [Google Scholar]
- Tomaštík, J.; Mokroš, M.; Saloň, Š.; Chudý, F.; Tunák, D. Accuracy of photogrammetric UAV-based point clouds under conditions of partially-open forest canopy. Forests 2017, 8, 151. [Google Scholar] [CrossRef]
- Júnior, L.; Ferreira, M.; Côrtes, J.; Jorge, L. High accuracy mapping with cartographic assessment for a fixed-wing remotely piloted aircraft system. J. Appl. Remote Sens. 2018, 12, 014003. [Google Scholar]
- Prajwal, M.; Rishab, J.; Vaibhav, S.; Karthik, K.S. Optimal number of ground control points for a UAV based corridor mapping. Int. J. Innov. Res. Sci. Eng. Technol. 2016, 5, 28–32. [Google Scholar]


| Specifications | DJI Phantom 3 Advanced | DJI Phantom 4 Professional |
|---|---|---|
| Weight | 1280 g | 1388 g |
| Diagonal size | 350 mm | 350 mm |
| Max speed | 57.6 km/h | 72.0 km/h |
| Max serve celling MSL | 6000 m | 6000 m |
| Max flight time | 23 min | 30 min |
| GNSS | GPS/GLONASS | GPS/GLONASS |
| Camera lens | FOV 94°, 20 mm, f/2.8 | FOV 84°, 24 mm, f/2.8-f11 |
| Image sensor | 1/2.3” CMOS, 12.4M pixels | 1” CMOS, 20.0M pixels |
| Hover Accuracy | ||
| Vertical: | ±0.1 m (with Vision Positioning) | ±0.1 m (with Vision Positioning) |
| ±0.5 m (with GPS Positioning) | ±0.5 m (with GPS Positioning) | |
| Horizontal: | ±0.3 m (with Vision Positioning) | ±0.3 m (with Vision Positioning) |
| ±1.5 m (with GPS Positioning | ±1.5 m (with GPS Positioning |
| Date of Flight | Number of Photos Used for the Mosaic | Spatial Resolution of the Mosaic (cm) | Drone Model Used |
|---|---|---|---|
| 9/7/2017 | 378 | 2.73 | Phantom 4 |
| 10/17/2017 | 288 | 2.95 | Phantom 3 |
| 11/13/2017 | 288 | 2.95 | Phantom 3 |
| 12/14/2017 | 286 | 2.89 | Phantom 3 |
| 1/15/2018 | 230 | 2.78 | Phantom 3 |
| 2/15/2018 | 306 | 2.89 | Phantom 3 |
| 3/6/2018 | 168 | 2.57 | Phantom 4 |
| Date | 9/7 2017 | 10/17 2017 | 11/13 2017 | 12/14 2017 | 1/15 2018 | 2/15 2018 | 3/6 2018 |
|---|---|---|---|---|---|---|---|
| Time | 10:00 | 10:30 | 10:30 | 12:00 | 14:15 | 12:30 | 9:30 |
| Temperature (C) | 26.1 | 24.4 | 17.8 | 13.3 | 6.1 | 22.8 | 20.0 |
| Dew Point (C) | 11.1 | 3.9 | 15.0 | 1.7 | 5.6 | 18.3 | −6.1 |
| Humidity (%) | 39 | 26 | 83 | 45 | 97 | 76 | 17 |
| Wind Direction | Variable | ENE | NE | NNW | N | S | NNW |
| Wind Speed (km/h) | 8.1 | 11.3 | 9.7 | 4.8 | 16.1 | 11.3 | 22.5 |
| Wind Gust (km/h) | 0 | 0 | 0 | 0 | 0 | 0 | 35.4 |
| Pressure (mm Hg) | 757 | 757 | 759 | 752 | 762 | 752 | 752 |
| Weather Condition | Fair | Fair | Cloudy | Fair | Cloudy | Mostly Cloudy | Fair |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hung, I.-K.; Unger, D.; Kulhavy, D.; Zhang, Y. Positional Precision Analysis of Orthomosaics Derived from Drone Captured Aerial Imagery. Drones 2019, 3, 46. https://doi.org/10.3390/drones3020046
Hung I-K, Unger D, Kulhavy D, Zhang Y. Positional Precision Analysis of Orthomosaics Derived from Drone Captured Aerial Imagery. Drones. 2019; 3(2):46. https://doi.org/10.3390/drones3020046
Chicago/Turabian StyleHung, I-Kuai, Daniel Unger, David Kulhavy, and Yanli Zhang. 2019. "Positional Precision Analysis of Orthomosaics Derived from Drone Captured Aerial Imagery" Drones 3, no. 2: 46. https://doi.org/10.3390/drones3020046
APA StyleHung, I.-K., Unger, D., Kulhavy, D., & Zhang, Y. (2019). Positional Precision Analysis of Orthomosaics Derived from Drone Captured Aerial Imagery. Drones, 3(2), 46. https://doi.org/10.3390/drones3020046




