1. Introduction
Over the last few decades, unmanned aerial vehicles (UAVs) have had significant development in many aspects, including fixed-wing designs, hovering multi-copters, sensor technology, real-time algorithms for stabilization and control, autonomous waypoint navigation. In recent years, Micro-UAVs (weight ≤ 3 kg), also known as Micro Aerial Vehicles (MAVs) have had wide adoption in many applications, including aerial photography, surveillance, reconnaissance, and environmental monitoring, to name a few. Although MAVs are highly effective for such applications, they still face many challenges, such as a short operational range and limited computational power of the onboard processors, mainly due to their battery life and/or limited payload. Most MAVs currently in use usually employ a rechargeable lithium polymer (LiPo) battery that can provide a higher energy density than other battery types, but they still have a very limited flight endurance of about 10–30 min at best.
To overcome these issues, a number of solutions have been proposed, including integration of a tether for power and data transmission [
1], autonomous deployment and recovery from a charging station [
2], solar-powered photovoltaic (PV) panels [
3], and development of batteries with high-power density. The most straightforward approach, without a doubt, would be to increase battery capacity, such as with a lightweight hydrogen fuel cell [
4], but such batteries are still expensive and heavy for small-scale UAVs. Alternatively, tethered flights with a power transmission line can support hypothetically large-scale flight endurance; however, the operational range of tethered flight is intrinsically limited to the length of the power line. The solar panel methods are attractive for relatively large fixed-wing UAVs, but they are not quite suitable for most rotary-wing UAVs.
Autonomous takeoff from and landing on a mobile platform with a charging or battery swapping station offers an attractive solution in circumstances where continuous flight tasks with an extended operational range are desired. In these scenarios, the UAV becomes an asset to the ground vehicle, where the UAV can provide aerial services such as mapping for the purposes of path planning. For example, emergency vehicles, delivery trucks, and marine or ground carriers could be used for deploying UAVs between locations of interest and as mobile charging stations [
2,
5,
6,
7].
Other examples, especially for large-scale UAVs, include autonomous takeoff and landing on a moving aircraft carrier or a naval ship [
8,
9,
10]. Autonomous takeoff and landing also allow more efficient deployment and recovery for a large fleet of UAVs without human intervention.
In this paper, we present a complete system architecture enabling a commercially available micro-scale quadrotor UAV to land autonomously on a high-speed mobile landing platform under various wind disturbances. To this end, we have developed an efficient control method that can be implemented on an embedded system at low cost, power, and weight. Our approach consists of (i) vision-based target position measurement; combined with (ii) a Kalman filter for optimal target localization; (iii) model predictive control for guidance of the UAV; and (iv) integral control for robustness.
The rest of the paper is organized as follows. In
Section 2 we discuss various techniques associated with autonomous UAV landing. In
Section 3 we present the overall system architecture.
Section 4 presents the dynamic model of the UAV for this study, optimal target localization for the landing platform, and the model predictive control for the UAV.
Section 5 presents simulation results to validate our approach, and we conclude in
Section 6.
2. Related Work
The major challenges in autonomous landing are (i) accurate measurements (or optimal estimates) of the locations of the landing platform as well as the UAV and (ii) robust trajectory following in the presence of disturbances and uncertainties. To face these challenges, several approaches for autonomous landing of rotary-wing UAVs have been proposed. Erginer and Altug have proposed a PD controller design for attitude control combined with vision-based tracking that enables a quadcopter to land autonomously on a stationary landing pad [
11]. Voos and Nourghassemi have presented a control system consisting of an inner loop attitude control using feedback linearization, an outer loop velocity and altitude control using proportional control, and a 2D-tracking controller based on feedback linearization for autonomous landing of a quadrotor UAV on a moving platform [
12]. Ahmed and Pota have introduced an extended backstepping nonlinear controller for landing of a rotary wing UAV using a tether [
13].
Robust control techniques also have been used for UAV landing to deal with uncertain system parameters and disturbances. Shue and Agarwal have employed a mixed
control technique, where the
method is used for trajectory optimization and the
technique minimizes the effect of the disturbance on the performance output [
14]. Wang et al. have also employed a mixed
technique to ensure that the UAV tracks the desired landing trajectory under the influence of uncertainties and disturbances [
15]. In their approach, the
method has been formulated as a linear quadratic Gaussian (LQG) problem for optimal dynamic response and the
method has been adopted to minimize the ground effect and atmospheric disturbances.
Computer vision has been used in a crucial role in many autonomous landing techniques. Lee et al. [
16] have presented image-based visual servoing (IBVS) to track a landing platform in two-dimensional image space. Serra et al. [
17] have also adopted dynamic IBVS along with a translational optimal flow for velocity measurement. Borowczyk et al. [
18] have used AprilTags [
19], a visual fiducial system, together with an IMU and GPS receiver integrated on a moving target travelling at a speed of up to 50 km/h. Beul et al. [
20] have demonstrated autonomous landing on a golf cart running at a speed of ~4.2 m/s using two cameras for high-frequency pattern detection in combination with an adaptive yawing strategy.
Learning-based control methods for autonomous landing have also been studied to achieve the optimal control policy under uncertainties. Polvara et al. [
21] have proposed an approach based on a hierarchy of deep Q-networks (DQNs) that can be used as a high-end control policy for the navigation in different phases. With an optimal policy, they have demonstrated a quadcopter autonomously landing in a large variety of simulated environments. A number of approaches based on adaptive neural networks have also been adopted to render the trajectory controller more robust and adaptive, ensuring that the controller is capable of guiding aircraft to a safe landing in the presence of various disturbances and uncertainties [
22,
23,
24,
25].
Model Predictive Control (MPC) is a control algorithm that utilizes a process model to predict the states over a future time horizon and compute its optimal system inputs by optimizing a linear or quadratic open-loop objective subject to linear constraints. Researchers already have it implemented in other problems. Templeton et al. [
26] have presented a terrain mapping and analysis system to autonomously land a helicopter on an unprepared terrain based on MPC. Yu and Xiangju [
27] have implemented a model predictive controller for obstacle avoidance and path planning for carrier aircraft launching. Samal et al. [
28] have presented a neural network-based model predictive controller to handle external disturbances and parameter variations of the system for the height control of a unmanned helicopter. Tian et al. [
29] have presented a method that combined an MPC with a genetic algorithm (GN) to solve a cooperative search problem of UAVs.
3. System Overview
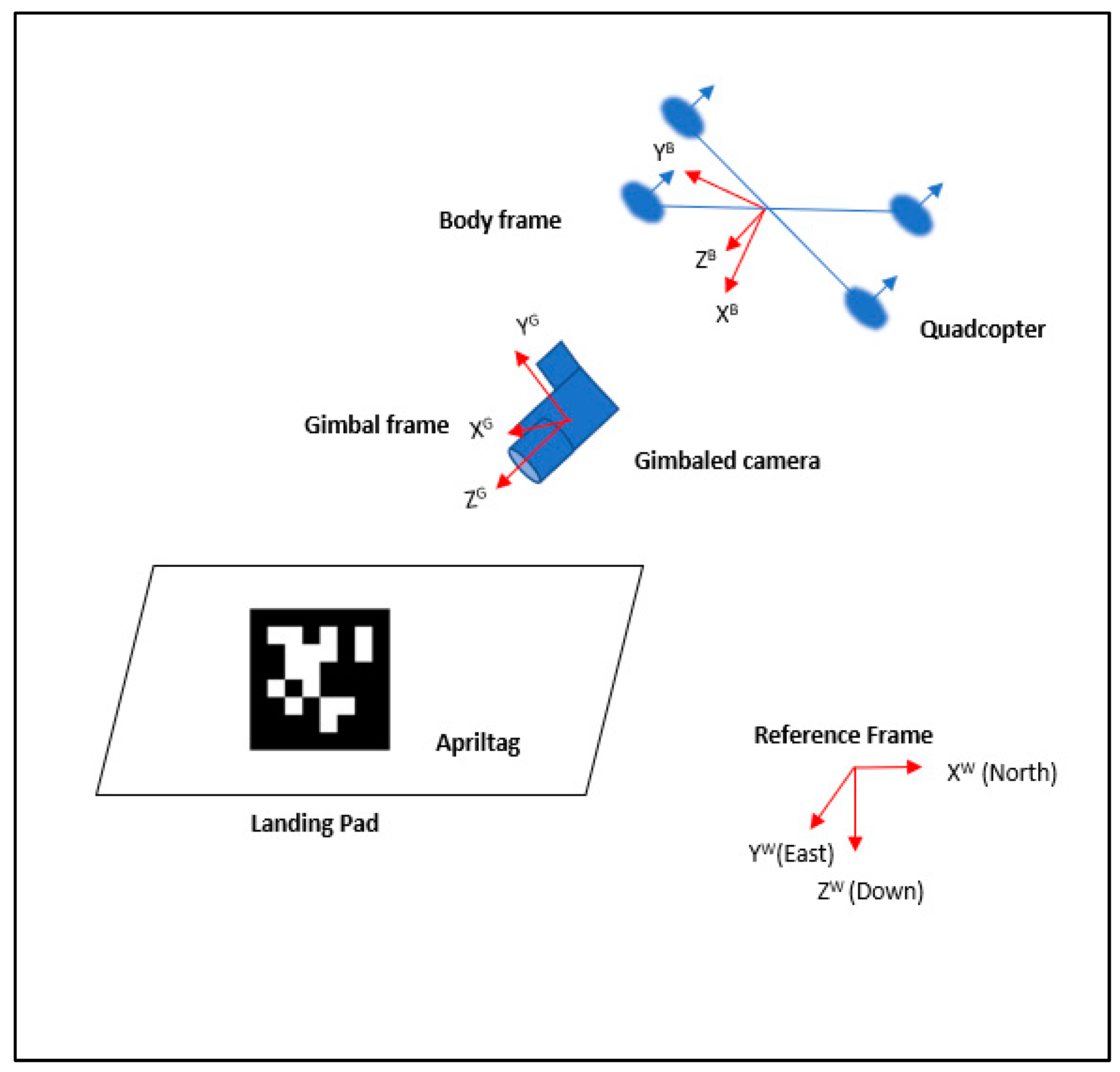
The UAV used in this work is a DJI Matrice 100 quadrotor, which is shown in
Figure 1. It is equipped with a gimbaled camera, an Ubiquiti Picostation for Wi-Fi communication, a flight control system (autopilot), a 9-axis inertial measurement unit (IMU), and a GPS receiver. The flight control system has an embedded extended Kalman filter (EKF), which provides the position, velocity, and acceleration of the UAV at 50 Hz. The gimbaled camera is employed to detect and track the visual markers placed on the landing platform at 30 Hz, which is in turn used to localize the landing platform when the distance between the UAV and the landing platform is very close, e.g., less than 5 m. The Picostation is the wireless access point for long distance communication between the landing platform and the UAV. We have also integrated a DJI Guidance, an obstacle detection sensor module, to accurately measure the distance between the UAV and the landing platform at, or right before, landing to decide if the UAV has landed.
The mobile landing platform used in this work is equipped with an embedded system interfaced with a GPS receiver, an IMU, and a Wi-Fi module that can transmit the position and velocity of the landing platform to the UAV at 10 Hz. The visual marker used is a matrix barcode (An “AprilTag” to be specific) shown in
Figure 2. The AprilTag is mounted on the landing platform for visual tracking of the landing platform by the UAV. We have adopted a Robot Operating System (ROS) software package that provides an ROS wrapper for the AprilTag library, enabling us to obtain the position and orientation of the tag with respect to the camera. One of the advantages of using AprilTags in this work is to minimize the effort in object recognition for vision-based target tracking.
With the position of the target (or AprilTag) with respect to the camera position, we can easily obtain the desired gimbal angle for the camera to point at the target. In other words, we always want to have the target at the center of the image plane captured by the camera to minimize the probability of target loss. The desired gimbal angle can be obtained by
where
and
are, respectively, the desired pitch and yaw angle of the gimbal;
and
are, respectively, the current pitch and yaw angle of the gimbal;
and
are, respectively, the lateral and longitudinal position of the target on the image plane coordinates; and
is the distance between the target and the camera. Since the roll of the gimbal is only ±15 degrees, we do not use it for target tracking. The desired gimbal angles are computed every time an AprilTag is detected (~30 Hz) and sent to a proportional derivative (PD) controller for the gimbaled camera to track the landing platform in a timely fashion.
5. Simulation Results
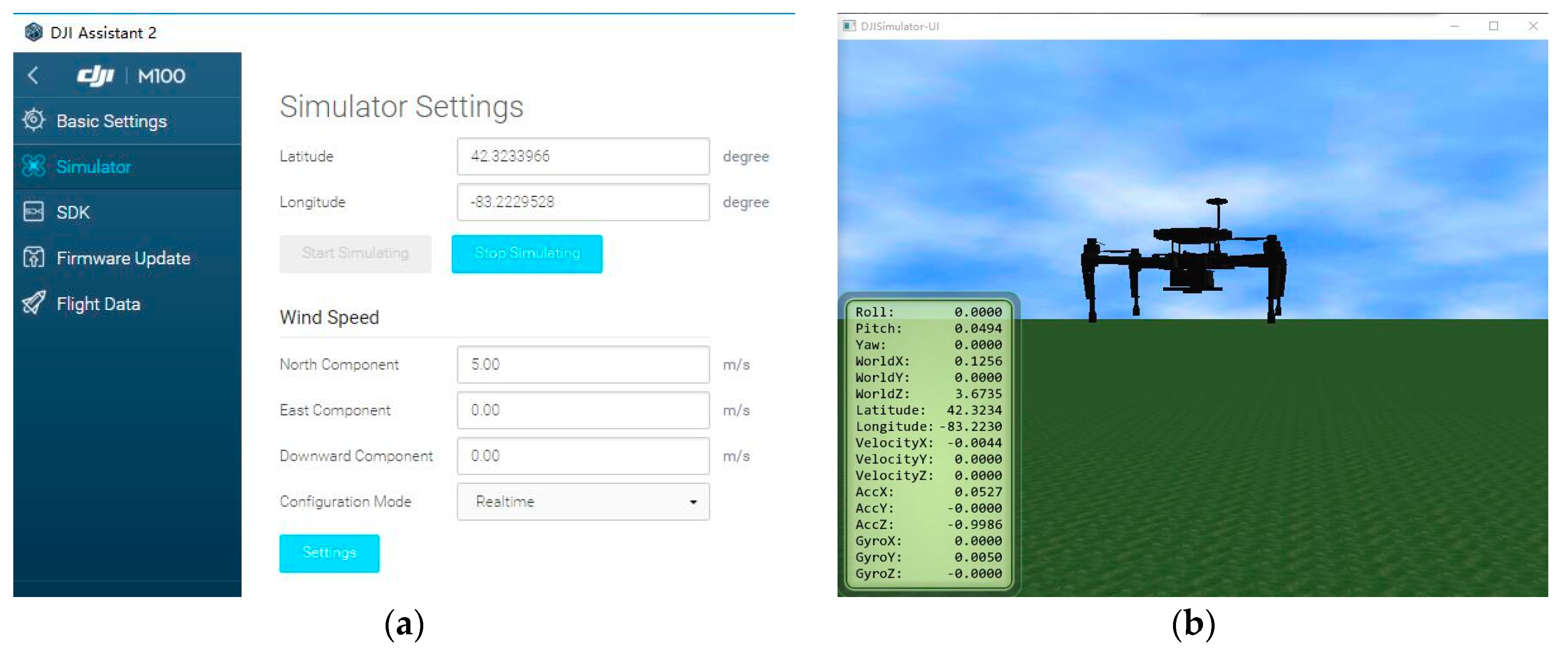
To validate our control method for autonomous landing on a moving platform, we used the DJI hardware-in-the-loop (HITL) simulation environment. As shown in
Figure 3a, the control panel of the HITL provides the initial settings for flight simulations as well as wind disturbances.
5.1. Localization the Landing Platform
At the beginning of autonomous landing tasks, our target localization algorithm relies on the position and velocity data transmitted from the landing platform. At this stage, the position data are measured by the GPS receiver integrated with the landing platform. As the UAV approaches the landing platform, the UAV still relies on the GPS data until the distance between the UAV and the landing platform is close enough for the landing platform to be observed by the camera. At this stage, we use the distance measurements from the AprilTag detection algorithm. A video stream obtained from the camera is processed at a ROS at 30 Hz to obtain the position of the AprilTag in the camera frame. Then, we calculate the position of the AprilTag in the reference frame.
In order to validate the performance of the Kalman filter, we introduced additive white Gaussian noise (AWGN), with its standard deviation of 0.03 () in the position measurements to simulate the measurement error from the Apriltag detection and of 0.18 () in the velocity measurements to simulate the velocity measurement error. We found these sensor noises empirically.
The measurement noise covariance matrix for the Kalman filter is given by
where
,
,
, and
are the variances of sensor noise of the lateral position, longitudinal position, lateral velocity, and longitudinal velocity, respectively. So, we set
and
. The state transition covariance matrix is given by
where
is the time step and
is the estimated variance of the acceleration of the landing platform. In this work, we have
0.025 s and
.
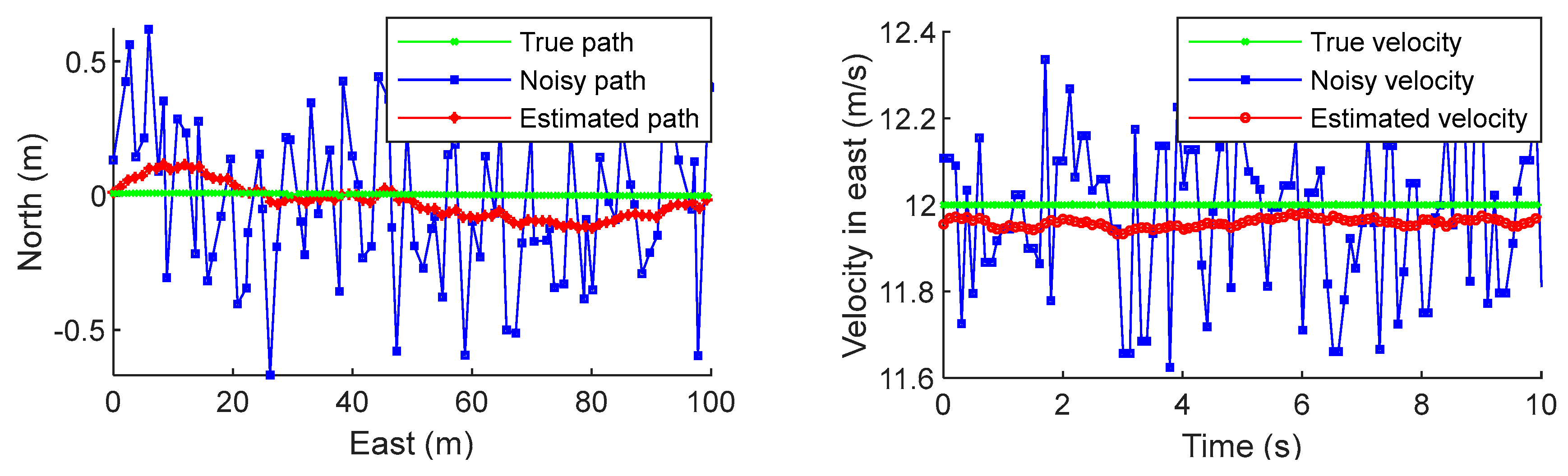
Figure 4 shows the estimated position and velocity of the landing platform obtained from the Kalman filter. The root mean square (RMS) errors are 7.97 cm for the position and 0.0336 m/s for the velocity of the landing platform, which are satisfactory for a 1.15m wingspan quadcopter to land on it.
The startup situations are all the same: the target starts at 50 m in the north from the origin and moves toward east with constant 12 m/s speed, and at the same time, the UAV starts at the origin with zero initial speed. The UAV first enters the approach state and tracks the target until the UAV is on the top of target, and then enters the landing state and starts to land on the target.
5.2. Selection of MPC Parameters
For this study, we set for the prediction horizon and for the control horizon, with a sampling time of 0.025 s. Consequently, for every time step, the MPC optimizes the flight trajectory of the UAV for the next 0.3 s. For the state weight matrix Q, the weights for both the longitudinal and the lateral positions are set to 10 for the first seven prediction steps out of 12 steps, the weights for both the longitudinal and the lateral velocities are set to 1.5 for the last five prediction steps, and all the rest are set to 1. For the input weight matrix R, we simply set it to the identity matrix. The mass of the UAV is 2.883 kg.
5.3. Straight Path without Wind Disturbance
We have tested our method with various speeds set for the landing platform. In this experiment, we assume that the sensor outputs have been contaminated by noise, and therefore the estimates of the target location are obtained through the Kalman filter discussed in
Section 5.1.
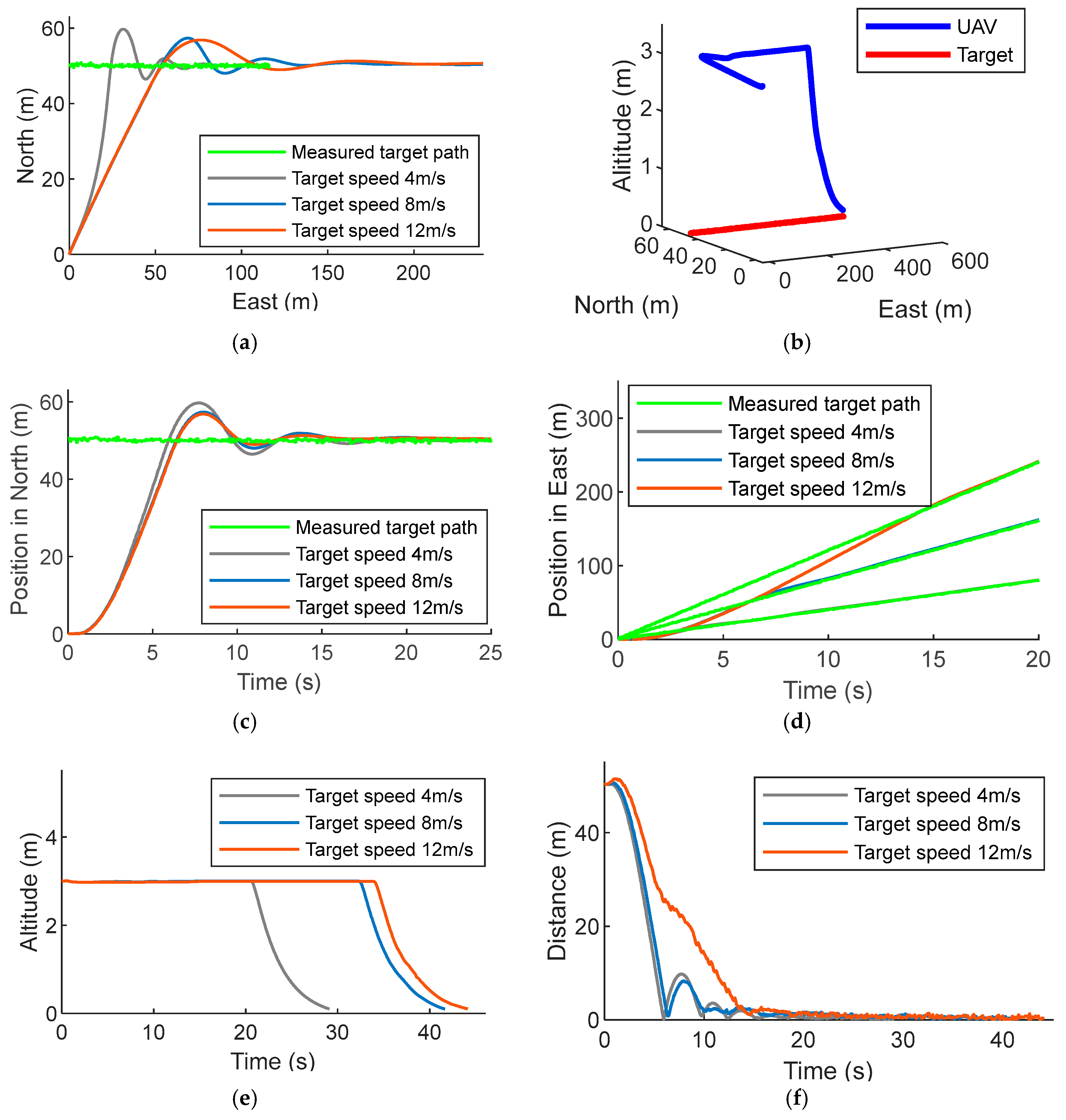
Figure 5 demonstrates the performance of the MPC for approaching and landing on the platform traveling at the speeds of 4 m/s, 8 m/s, and 12 m/s. The trajectories of the UAV following and landing on the platform travelling on a straight path are shown in
Figure 5a. It is apparent that it takes more time for the UAV flying at 12 m/s to approach and land on the target than for the UAV flying at 4 m/s performing the same task.
Figure 5b shows in 3D that the UAV has landed on the landing platform moving at 12 m/s on a straight path.
Figure 5c,d show the position in north and east of the UAV along with the measured location of the landing platform. As shown in
Figure 5e, the UAV maintains the altitude while it is approaching the landing platform and if the distance between the UAV and the landing platform becomes less than 1 m, the UAV starts descending.
Figure 5f shows the distance between the UAV and the landing platform. In these simulations, we have used the vertical distance between the UAV and the landing platform to decide if the UAV has landed (DJI Guidance discussed in
Section 3 can provide this quantity in flight experiments).
Table 1 summarizes the performance for the three different speeds of the landing platform with and without measurement noise. As the speed of the landing platform increases, the approach time, landing time, and landing error also increase. For the noisy measurements of the platform position and velocity, the UAV demonstrates similar approach time and landing time as the no noise case. The largest landing error with noisy measurements is 26 cm from the center of the landing platform, which shows that the method proposed in this work can be considered as a viable solution for autonomous landing on a moving platform.
5.4. Straight Path with Wind Disturbance
To validate the robustness of our method under wind disturbances, we implemented an integral controller that can be seamlessly fused with the MPC. We conducted simulations with a wind speed of 5 m/s and a target speed of 8 m/s. The integral controller is designed to accumulate the position error to fight against the wind.
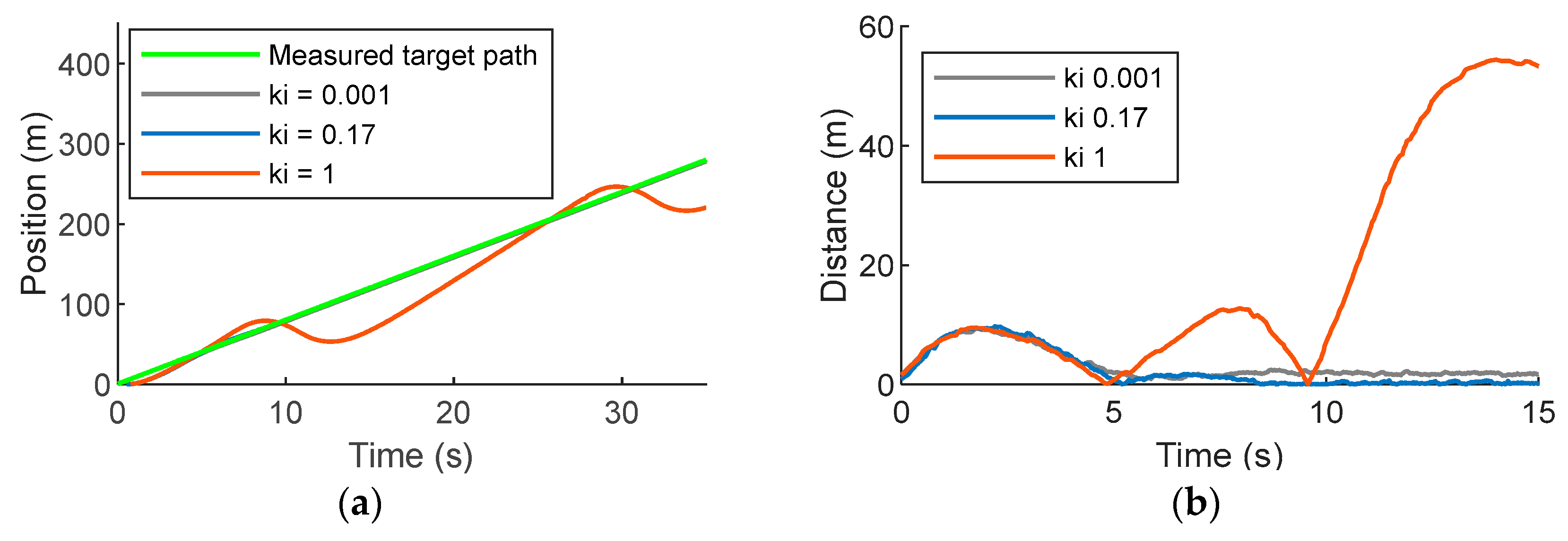
Figure 6 shows that the UAV reaches the desired position in approximately 9 s with zero steady-state error when the integral constant of
. If
is too small (e.g.,
), the UAV cannot reach the desired target position, with a steady-state error of approximately 1.6 m. For a large value of
(e.g.,
), the closed-loop system becomes unstable as shown in
Figure 6b.
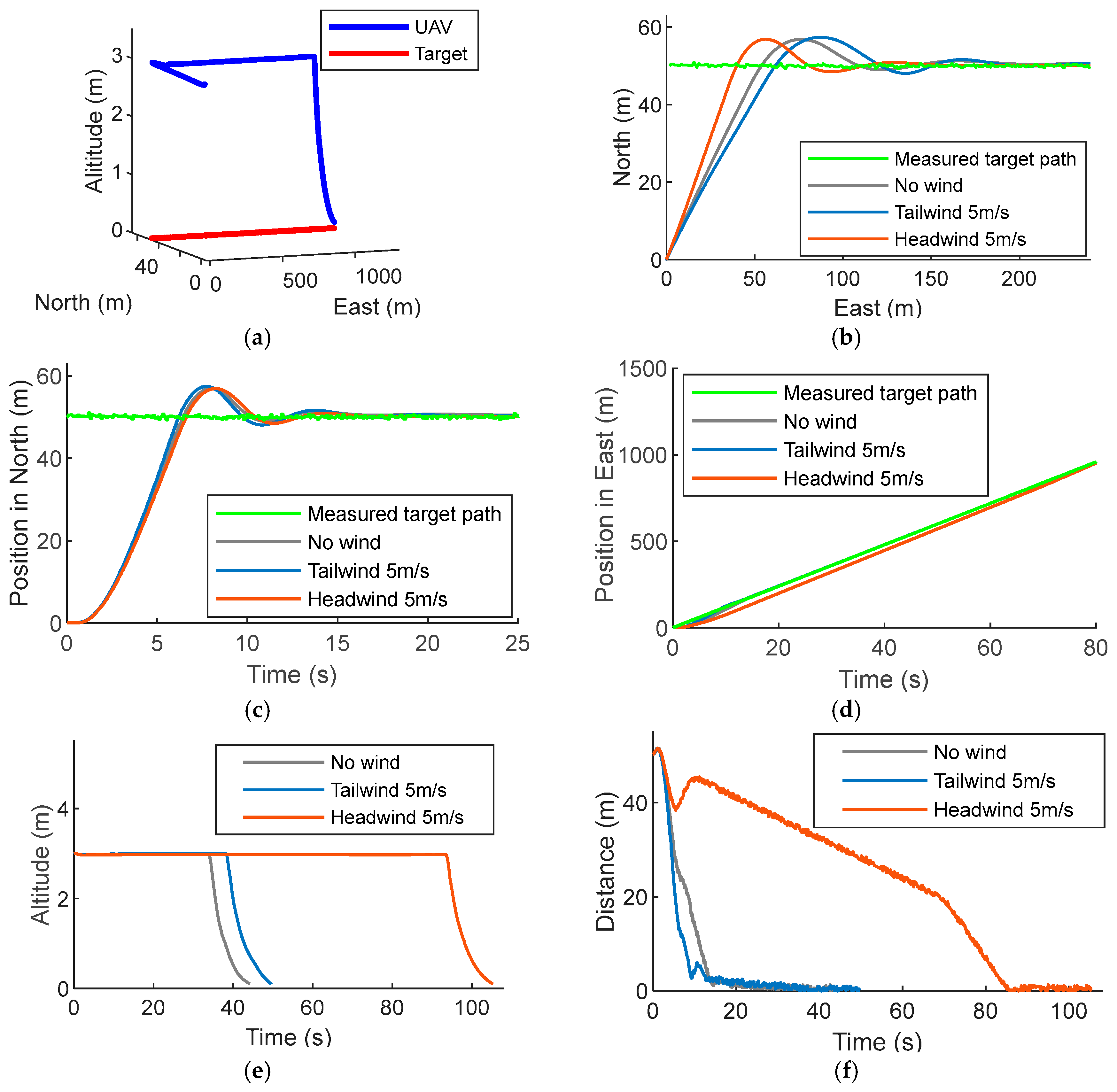
Figure 7a shows the trajectories of the UAV following and landing on the platform travelling on a straight path in the presence of a wind disturbance with a constant speed of 5 m/s. Since the UAV in this work can fly at a speed of up to 18 m/s, the maximum target speed we set in the simulations is 12 m/s for a headwind speed of 5 m/s.
Figure 7b–d shows the measured location of the landing platform and the trajectories of the UAV in no wind, a 5 m/s tailwind and a 5 m/s headwind. It is apparent that a tailwind has minimal effect on approach time, landing time, and landing error, while a headwind makes the UAV slow down. As shown in
Figure 7e,f, it is evident that the approach time dramatically increases with a headwind.
Table 2 summarizes the simulation results under the presence of wind disturbances. The approach time and landing time in the presence of a headwind disturbance are much greater than those in the presence of no wind or a tailwind. However, the landing error with a headwind is just slightly larger than the error with no wind. In case of noisy measurements, the landing error is still bounded by 37 cm, which shows that the method proposed in this work is robust enough for wind disturbances and noisy sensor measurements.
5.5. Curved Path
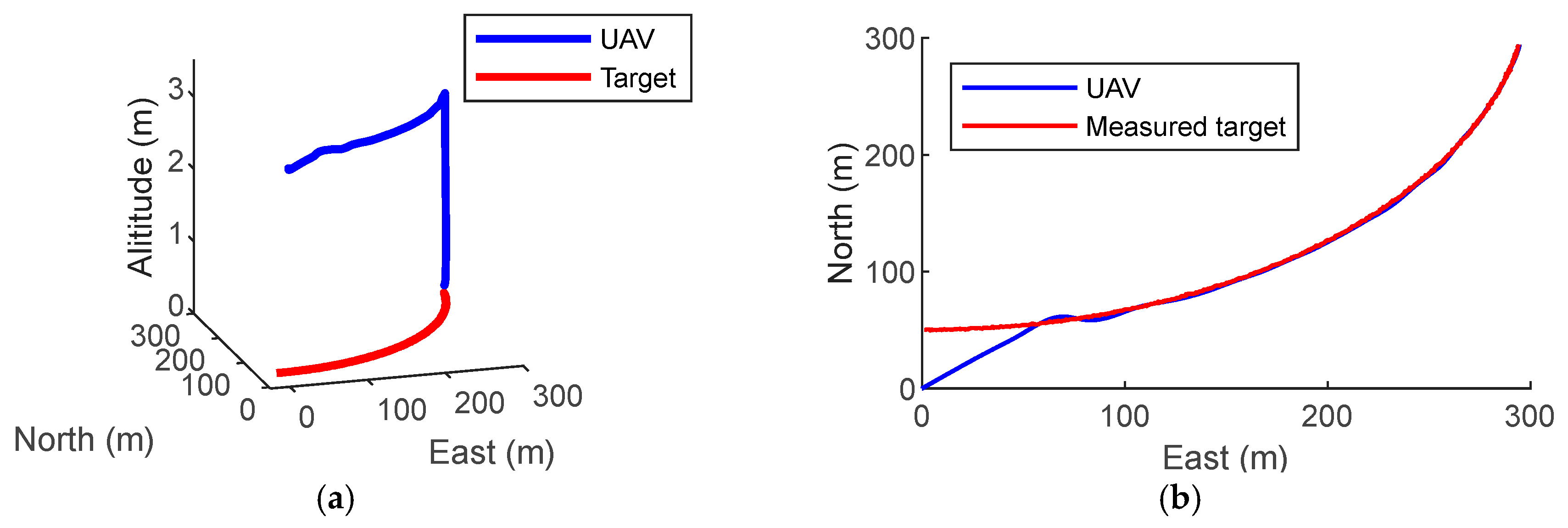
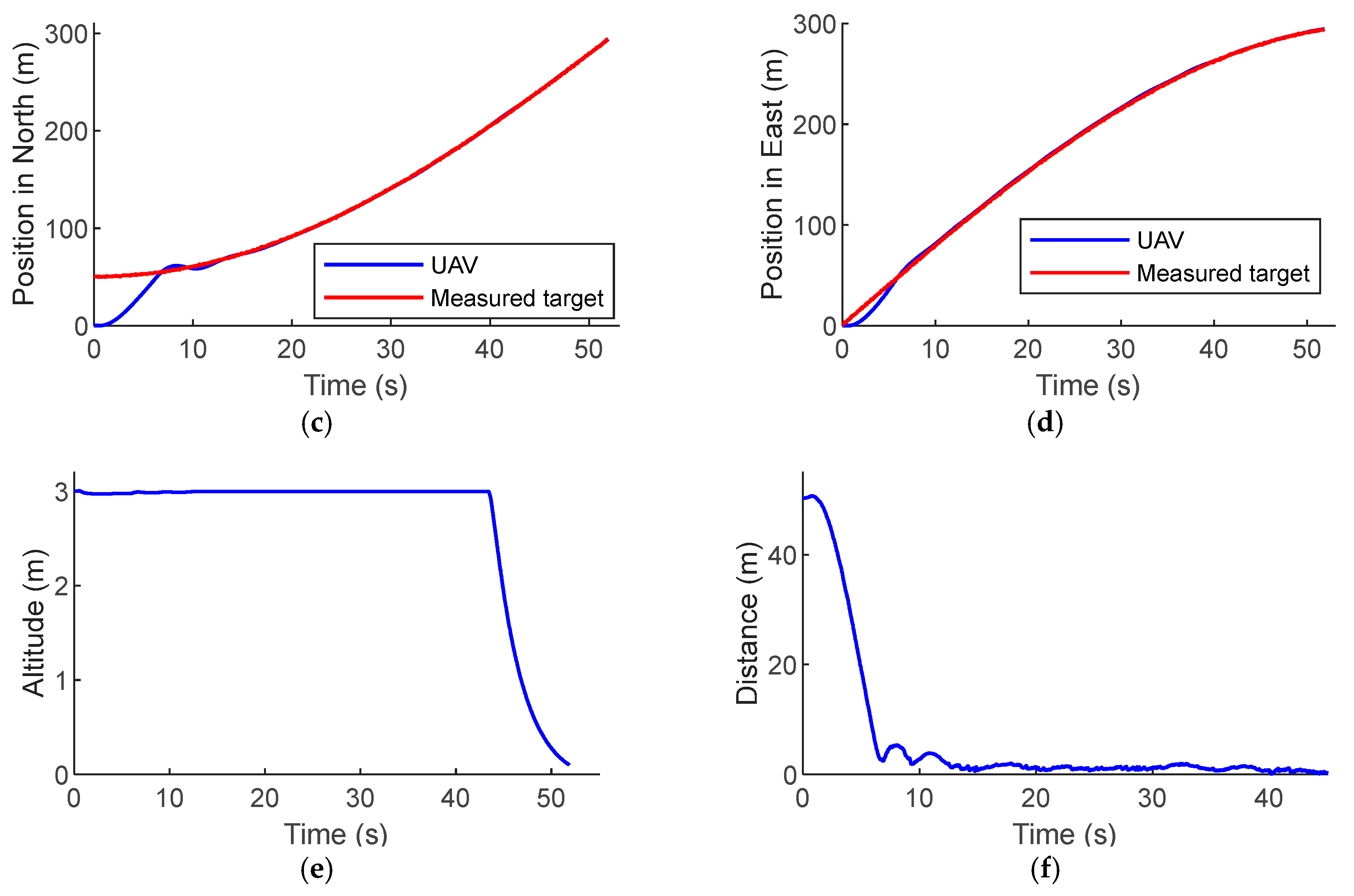
We also conducted simulations with the landing platform travelling on a curved path.
Figure 8a shows the UAV lading on a platform moving at 8 m/s on a curved path with a radius of 300 m. It is shown in
Figure 8b,c that it takes approximately 43 s for the UAV to approach the platform.
Figure 8e,f show that it takes an additional 9 s to land on the target, with a 35-cm error, which demonstrates that the proposed method is a viable solution for a landing platform traveling on a curved path as well as a straight path.
6. Conclusions and Future Work
In this work, we propose a new control method that allows a micro UAV to land autonomously on a moving platform in the presence of uncertainties and disturbances. Our main focus with this control method lies in the implementation of such an algorithm in a low-cost, lightweight embedded system that can be integrated into micro UAVs. We have presented our approach, consisting of vision-based target following, optimal target localization, and model predictive control, for optimal guidance of the UAV. The simulation results demonstrate the efficiency and robustness with wind disturbances and noisy measurements.
In the future, we aim to conduct flight experiments to validate the control methods we present in this paper. The landing platform can be a flat surface with a dimension of at least m for safe landing and it will be mounted on a vehicle (for example, a truck bed or a flat root of a golf cart). We will also develop robust recovery methods that can save the vehicle from various failures, such as communication loss between the UAV and the landing platform, that can occasionally occur in the real world.