Abstract
In this paper, a biologically-inspired distributed intelligent control methodology is proposed to overcome the challenges, i.e., networked imperfections and uncertainty from the environment and system, in networked multi-Unmanned Aircraft Systems (UAS) flocking. The proposed method is adopted based on the emotional learning phenomenon in the mammalian limbic system, considering the limited computational ability in the practical onboard controller. The learning capability and low computational complexity of the proposed technique make it a propitious tool for implementing in real-time networked multi-UAS flocking considering the network imperfection and uncertainty from environment and system. Computer-aid numerical results of the implementation of the proposed methodology demonstrate the effectiveness of this algorithm for distributed intelligent flocking control of networked multi-UAS.
1. Introduction
1.1. Motivation
Distributed coordination of networked multi-Unmanned Aircraft Systems (UAS) has been studied by diverse research communities in recent years [1,2,3,4]. Due to the broad applications of flocking in real-world scenarios, most of the networked multi-UAS control methodologies are adopted based on the mathematical model of flocking [5,6,7]. In general, three basic rules (i.e., separation, alignment, and cohesion) are considered for simulating the flocking behavior [1] which are observed in many living beings (i.e., birds, fish, bacteria, and insects) [8].
Several research groups have been contributed for improving the flocking behavior of networked multi-UAS in recent years [9,10,11,12]. Groups of aircrafts, in many applications involving networked multi-UAS, require communicating in order to successfully accomplish their assigned tasks. Network imperfection, e.g., delay, commonly exists in communication due to the limited communication resource and heavy traffic in the network [13,14]. As a result, it is of paramount importance to address the challenges of network-induced delay and taking the influence of network-induced delays into account in designing control algorithms for multi-unmanned aircraft systems. Besides network imperfections, the uncertainty from the complex environment and system dynamics is another critical challenge and cannot be ignored in advanced applicable control development. Therefore, it is important to consider the uncertainties from the environment and system in designing control algorithms.
1.2. Related Works
Diverse research groups have attempted to address the issues arising from the effects of network-induced delay in flocking control of multi-unmanned aircraft systems/multi-agent systems. For example, delay-independent flocking control of multi-agent systems have been addressed in [15,16]. Closely related, a distributed control design for the discrete-time directed multi-agent systems with distributed network-induced delay has been proposed in [17]. The authors in [18] presented a distributed algorithm for the sensor networks by considering the effects of the imperfect communication such as link failures and channel noise. In [19], the authors studied the design of distributed formation recovery control for nonlinear heterogeneous multi-agent systems. A distance constrained based adaptive flocking control for the multi-agent system with network-induced delay was investigated in [20]. Recently, coordinated control of two-wheel mobile robots with input network-induced delay was presented in [21]. Although all of these proposed methods perform well dealing with the effects of network-induced delay, they still need the detailed information of the system. In this regard, the development of control strategies for dealing with the network-induced delay with less dependency on the full knowledge of the system dynamics is of paramount importance.
In recent years, intelligent approaches have been extensively utilized for successfully solving diverse complex problems [22,23,24]. Among them, biologically-inspired intelligent approaches have received tremendous interest by many researchers because of their inherent potential to deal with computationally complex systems. Emotional Learning is one such approach, which takes advantage of a computational model of the amygdala in the mammalian limbic system [25]. This model, known as Brain Emotional Learning Based Intelligent Controller (BELBIC), consists of the Amygdala, Orbitofrontal Cortex, Thalamus, and Sensory Input Cortex as its main components. From a control systems point of view, BELBIC is a model-free controller (i.e., model dynamics are fully or partially unknown) that has shown promising performance under noise and system uncertainty [26].
Sensory Inputs () and Emotional Signal () are two main inputs to the BELBIC model, and it is shown that the multi-objective problems could be solved by defining appropriate and [27,28]. The flexibility in assigning different and makes this controller a practical tool for implementation in real-time applications. Furthermore, BELBIC could effectively control a system even when the states of the system and the controller performance feedback are the only available information [26]. In addition, compared to other existing learning-based intelligent control methods, the computational complexity of BELBIC is on the order of which makes it a suitable approach for real-time implementation.
1.3. Main Contributions
The main contribution of this paper is to develop a model-free distributed intelligent control methodology to overcome the challenges including the network-induced delay and uncertainties from the environment and system in networked multi-UAS. To this end, we propose a biologically-inspired distributed intelligent controller, which takes advantage of the computational model of emotional learning in the mammalian limbic system. Our recent work in [29] introduced the theoretical framework for the flocking control for networked multi-UAS using BELBIC. These results are improved upon and extended in this paper for accomplishing an intelligent and practical flocking of networked multi-UAS, when subjected to impacts from uncertain network imperfections. The proposed methodology has a low computational complexity, which makes it a promising method for real-time applications. Furthermore, keeping the system complexity in a practically achievable limit, the proposed method delivers a controller with multi-objective properties (i.e., control effort optimization, network-induced delay handling, and noise/disturbance rejection). Moreover, we provided the Lyapunov stability analysis to demonstrate that our proposed methodology guarantees the convergence of the designed control signals as well as maintaining the system stability during the learning. The learning capability of the proposed approach is validated for flocking control of multi-unmanned aircraft systems influenced by the network-induced delay with promising performance. Computer-based numerical results of the implementation of the proposed methodology demonstrate the effectiveness of this algorithm for distributed intelligent flocking control of networked multi-UAS.
In other words, the solution proposed in this paper is a model-free distributed intelligent controller, which provides the following benefits:
- The knowledge of system dynamics is not fully or partially required.
- It has the capabilities of overcoming the network-induced delay, handling the uncertainties, and noise/disturbance rejection.
- It is appropriate for real-time implementation due to its low computational complexity (i.e., the developed algorithm is a real-time applicable learning technique).
- It ensures the stability of the system.
The rest of the paper is organized as follows. Section 2 presents the problem formulation and some preliminaries about flock modeling with network-induced delay and emotional learning. Our main contribution is introduced in Section 3, which consists of a distributed intelligent flocking control strategy based on emotional learning. Section 4 presents numerical simulation results. The conclusions of the paper and future directions of our work are provided in Section 5.
2. Problem Formulation and Preliminaries
In this section, some preliminaries are provided and the problem formulation is briefly discussed. First, the dynamic of the networked multi-UAS is given; then, flock topology is modeled by means of a dynamic graph. Next, network-induced delay and BELBIC model are introduced, and, ultimately, the problem is formulated.
2.1. Flock Modelling
Assuming the movement of the flock in an m–dimensional space , the equation of motion of the ith agent with continuous-time double integrator dynamics could be described according to the following set of equations:
where is the control input, are position, and velocity of the ith agent, respectively. Consider a dynamic graph that consists of a set of vertices , and edges . Each vertex represents an agent of the flock while a communication link between a pair of agents is represented by an edge.
is the neighborhood set of agent i, where the range of interaction between agents i and agent j is defined by a positive constant r, and is the Euclidean norm in . Solving the set of algebraic conditions: , we could describe the geometric model of the flock, i.e., the -lattice [3], where the distance between two neighbors i and j is represented by a positive constant d.
To avoid the singularity of the collective potential function at , the -norm (i.e., ) is defined where , and is a positive constant. To resolve the singularity problem, the set of algebraic conditions can be rewritten as: .
A smooth collective potential function can be obtained by considering the above-mentioned constraints, where is a smooth pairwise potential function with , , and .
A possible choice for defining , which is a scalar bump function that smoothly varies between [0,1], is [3]:
is the flocking control algorithm introduced in [3], which consists of three main terms:
- (i).
- is the interaction component between two -agents and is defined as follows:where and are positive constants. The terms and are vector and the elements of the spatial adjacency matrix , respectively, which are described as follows:where , and for all i and q.
- (ii).
- is the interaction component between the -agent and an obstacle (named the -agent) and is defined as follows:where and are positive constants. and are position, and velocity of the kth obstacle (i.e., -agent), respectively. The terms and are vector and the elements of the heterogeneous adjacency matrix , respectively, which are defined as follows:is a repulsive action function and is the set of -neighbors of an -agent i, where the range of interaction of an -agent with obstacles is the positive constant . Here, , and
- (iii).
- is a goal component that consists of a distributed navigational feedback term and is defined as follows:where and are positive constants.
More detailed studies about flocking control algorithms can be found in [3].
Remark 1.
In practical networked multi-UAS flocking control systems, due to the complexity of the overall system, autonomous agents are commonly described by the double integrator dynamics. Since our analysis is focused on developing an intelligent distributed controller for flocking of networked multi-UAS, in this paper, the double integrator dynamics is adopted. Considering the fact that the double integrator dynamics is a very reduced dynamics of the quad rotorcrafts, one can extend our results by employing model-free inner-loop controllers in [23,30], etc.
2.2. Network-Induced Delays
Assuming that the state of agent i gets to agent j after passing through a communication channel with network-induced delay , the could be rewritten as:
In this paper, we consider the case where the network-induced delays in all channels are equal to . Although the delay is deterministic, it is unknown. The proposed method can effectively handle this unknown delay.
2.3. Brain Emotional Learning-Based Intelligent Controller
Brain Emotional Learning Based Intelligent Controller (BELBIC) is one of the neurobiologically-motivated intelligent methodologies, which is based on the computational model of emotional learning observed in the mammalian limbic system proposed in [25]. This model (depicted in Figure 1), has two main parts: Amygdala, and Orbitofrontal Cortex. Amygdala is responsible for immediate learning, while Orbitofrontal Cortex is responsible for inhibition of any inappropriate learning happening in the Amygdala. Sensory Inputs () and Emotional Signal () are two main inputs to the BELBIC model.
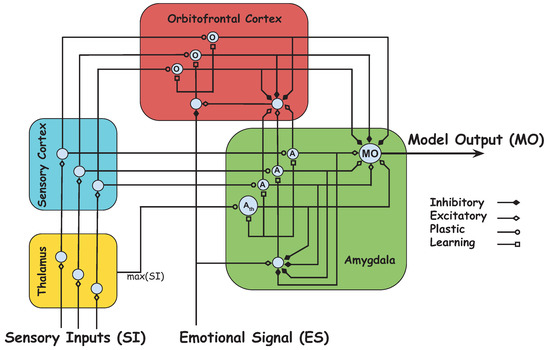
Figure 1.
Computational model of emotional learning.
The output of the BELBIC model () can be defined as
which is calculated by the difference between the Amygdala outputs () and the Orbitofrontal Cortex outputs (). Here, l is the number of sensory inputs.
The Orbitofrontal Cortex and the Amygdala outputs are calculated by the summation of all their corresponding nodes, where the output of each node is described as:
where is the lth sensory input, is the weight of the Amygdala, and is the weight of the Orbitofrontal Cortex. The following equations are employed for updating and , respectively:
where and are the learning rates.
The maximum of all is another input considered in the model. This signal (i.e., ), which is directly sent from the Thalamus to the Amygdala, is defined as:
where is the weight and the corresponding update law is the same as Equation (10).
Several techniques have been adopted for tuning the BELBIC parameters [26,31,32,33,34,35]. In this paper, to significantly reduce the computational complexity, a heuristic approach is utilized for tuning the BELBIC parameters.
2.4. Objectives
The objective is to design a biologically-inspired distributed intelligent controller for flocking control of multi-unmanned aircraft systems (i.e., , and n is the number of UASs), specifically, in the events of network-induced delay. The proposed intelligent control method is leveraging the computational model of emotional learning in the mammalian limbic system (i.e., BELBIC) introduced in Section 2.3, and is applied to the flocking model of networked multi-UAS described in Section 2.1.
In other words, the solution proposed in this paper is a model-free distributed intelligent controller, which is designed to maintain the motion of all agents in the flock in the events of network-induced delay.
3. Distributed Intelligent Flocking Control of Networked Multi-UAS Using Emotional Learning
3.1. System Design
Specifically, our focus is on the design of a biologically-inspired distributed intelligent controller for flocking of networked multi-UAS by using BELBIC because the implementation of it could be accomplished without increasing the complexity of the overall system. The BELBIC architecture implemented in this work is shown in Figure 2. This figure demonstrates a closed loop configuration that consists of the following blocks: (i) BELBIC block, (ii) Sensory inputs (SI) function block, (iii) Emotional signal (ES) generator block, and finally (iv) a block for the plant. This architecture implicitly demonstrates the overall emotional learning based control concept, which consists of the action selection mechanism, the critic, and the learning algorithm [26].
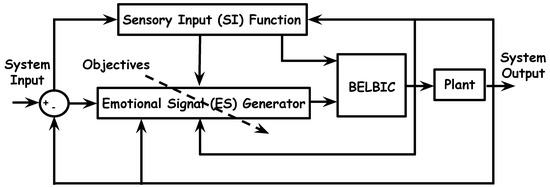
Figure 2.
Brain Emotional Learning Based Intelligent Controller (BELBIC) in the control loop.
3.2. Emotional Signal and Sensory Input Development
Fundamentally, BELBIC is an action selection technique, in which action is produced based on the sensory input () and the emotional signal (). The general forms of and are given as follows:
where e is the system error, r is the system input, y is the system output, and u is the control effort.
The control objectives (e.g., reference tracking and optimal control) could implicitly be decided by choosing the adequate . For example, it is possible to choose the for achieving a better reference tracking performance, for reducing the overshoot, and/or for the energy expense minimization, among others.
Aiming at designing a model-free distributed intelligent control for flocking control of multi-unmanned aircraft systems, the proposed biologically-inspired technique will focus on improving: (i) reference tracking performance, (ii) network-induced delay handling, and (iii) disturbance rejection.
To accomplish these objectives, for each of the control inputs (i.e., {,...,}), the and , will be designed as:
where , , , , , , and are positive gains. The will change its impact on the system behavior by assigning different values to these positive gains. In this work, different gains are assigned for each one of the control inputs (i.e., , ) of the system.
It should be mentioned that we designed the in such a way that the increase in reference tracking error will generate a negative emotion in the system, which is then taken as evidence for the unsatisfactory performance of the system. Therefore, the proposed controller will behave in such a way that it will always minimize the negative emotion, which leads to the satisfactory performance of the system.
3.3. Learning-Based Intelligent Flocking Control
In flocking control of networked multi-UAS, multiple performance considerations have to be taken into account all at the same time; therefore, it is a very interesting case for using biologically-inspired learning-based multi-objective methodologies like BELBIC. Designing a model-free distributed intelligent control for flocking of networked multi-UAS by considering the network-induced delay, in addition to designing a suitable controller for real-time implementation, encourages us to take advantage of the computational model of emotional learning in the mammals’ limbic system, i.e., BELBIC.
From Equations (15) and (16), the BELBIC-inspired distributed intelligent flocking control strategy for networked multi-UAS is defined as
Here, makes reference to each control input and n is the number of UASs. Considering the results obtained in Theorem 1 and by substituting the Emotional Signal with Equation (16), the BELBIC model output of the distributed intelligent control for flocking of networked multi-UAS could be obtained as follows:
which clearly satisfies our goal of distributed intelligent flocking control. In other words, the model output accomplished all the flocking properties i.e., Collision Avoidance, Obstacle Avoidance, and Navigational Feedback.
The overall model-free biologically-inspired distributed intelligent flocking control methodology proposed in this paper is summarized as a pseudo-code in Algorithm 1.
| Algorithm 1 : The BELBIC-inspired methodology for distributed intelligent flocking control of networked multi-UAS. |
| Initialization: |
| Set , , and , for . |
| Define network-induced delay. |
| Define Objective function, for . |
| for each iteration do |
| for each agent i do |
| Compute |
| Compute |
| Compute |
| Compute |
| Compute |
| Compute |
| Update |
| Update |
| Update |
| end for |
| end for |
3.4. Stability Analysis
Theorem 1 is presenting the convergence of the weights of the Amygdala () and the Orbitofrontal Cortex (). Theorem 2 is providing the closed-loop stability of the proposed controller and Remark 2 explains how the proposed method converges to distributed intelligent flocking control of networked multi-UAS.
Theorem 1.
Given the BELBIC design as Equations (15)–(18), there exists the positive BELBIC tuning parameters, , satisfying
- I.
- II.
such that the BELBIC estimated weights of the Amygdala () and the Orbitofrontal Cortex () converge to the desired targets asymptotically.
Proof.
See Appendix A. ☐
Theorem 2.
(Closed-loop Stability): Given that the initial networked multi-UAS state and the BELBIC estimated weights of the Amygdala () and the Orbitofrontal Cortex () are bounded in the set Λ, let the BELBIC be tuned and estimated control policy be given as Equations (10), (11) and (17), respectively. Then, there exist positive constants, , , satisfying Theorem 1 such that networked multi-UAS state, and BELBIC weight estimation errors are all asymptotically stable.
Proof.
See Appendix B. ☐
Remark 2.
Based on the BELBIC theory [26] and (Equation (17)), the distributed intelligent flocking control of networked multi-UAS can be obtained while the estimated weights of the Amygdala () and the Orbitofrontal Cortex () are converging to desired targets. According to Theorem 1, estimated weights converge to desired targets asymptotically. Therefore, the designed BELBIC input (i.e., Equation (17)) converges to distributed intelligent flocking control of networked multi-UAS asymptotically.
4. Simulation Results
This section presents computer-based simulation results showing the performance of the proposed biologically-inspired distributed intelligent flocking control of multi-unmanned aircraft systems (Section 4.2) and multi-unmanned ground systems (Section 4.1) in an obstacle-free environment. A total of 50 unmanned aircraft and 150 unmanned ground vehicles (UGVs) where employed, with initial velocities equal to zero, and positions randomly distributed in a squared area. The following parameters are used through the simulation: , , , . For the -norm, the parameter , for the parameters , for the bump functions and , and , respectively. The same network-induced delays (i.e., , ) are considered for all unmanned aircrafts and unmanned ground vehicles. All simulations are carried out on a platform with following specifications: Windows Server 2012 R2 standard, Processor: Intel(R) Xeon(R) CPU E5-2680 0 @ 2.70 GHz (4 processors), RAM: 8.00 GB.
4.1. Flocking of UGVs in an Obstacle-Free Environment
Figure 3 shows two snapshots of the simulation of the multi-unmanned ground systems in the obstacle-free environment. Figure 3 Left shows the 150 UGVs in their initial positions at s while Figure 3 Right shows the UGVs at s where they are flocking and have successfully formed a connected network.
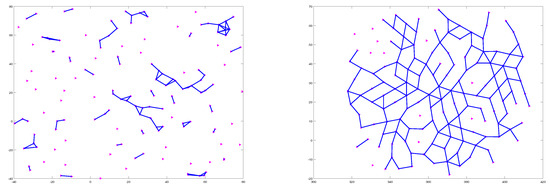
Figure 3.
Simulation in an obstacle-free environment. (Left) 150 UGVs randomly distributed in a squared area at s. (Right) at s, the 150 UGVs are flocking and have successfully formed a connected network.
For comparison purposes, two similar experiments were performed, but using the flocking algorithm introduced in [3], and Multirobot Cooperative Learning for Predator Avoidance (MCLPA) flocking algorithm introduced in [36] instead of the proposed algorithm. Figure 4 shows the velocities of all UGVs on the x- and y-axis for all methods in an obstacle-free environment under the influence of the networked-induced delay. The plot shows that, although the delay is deterministic, it is unknown and the proposed method could effectively handle the influences of the network-induced delay.
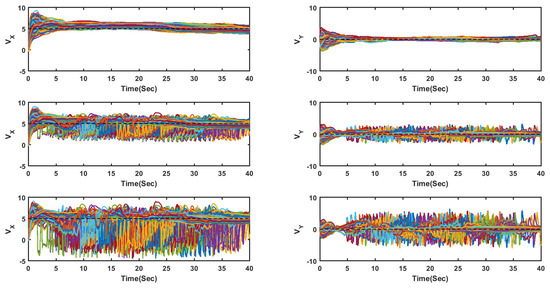
Figure 4.
Velocities of all UGVs on the x- and y-axis for all methods in an obstacle-free environment under the influence of the networked-induced delay. The proposed method (top row), the MCLPA [36] (middle row), and the flocking algorithm proposed in [3] (bottom row).
Figure 5 shows the Mean Square Error (MSE) of the velocities of the overall group of agents, for the flocking methods in [3], the MCLPA flocking strategy in [36], and the BELBIC-based flocking, when evolving in an obstacle-free environment.
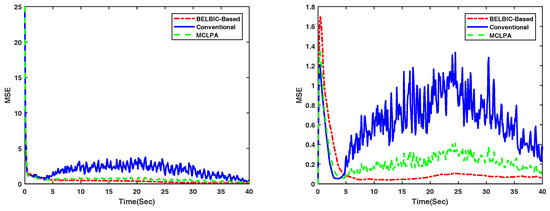
Figure 5.
Mean Square value of the velocities of all UGVs on the x-axis–(Left) and y-axis–(Right) generated by the overall group of agents when flocking in an obstacle-free environment. The BELBIC-based flocking is presented in dot-dashed red, the MCLPA flocking strategy in [36] in dashed green, and the flocking in [3] in solid blue. Notice that the MSE of the BELBIC-based flocking are smaller, and therefore more appropriate to implement in real-robots.
Table 1 shows the characteristics of the MSE of velocities of all flocking strategies for UGVs in the obstacle-free environment.

Table 1.
Characteristics of the MSE of all flocking strategies for UGVs in the obstacle-free environment.
4.2. Flocking of UASs in an Obstacle-Free Environment
Figure 6 shows two snapshots of the simulation of the multi-unmanned aircraft systems in the obstacle-free environment. Figure 6 Left shows the 50 UASs in their initial positions at s while Figure 6 Right shows the UASs at where they are flocking and have successfully formed a connected network.
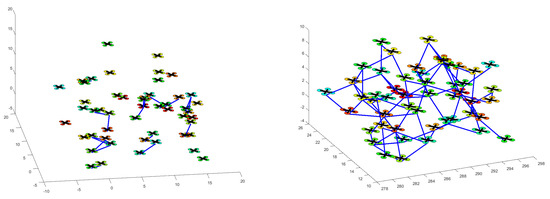
Figure 6.
Simulation in an obstacle-free environment. (Left) 50 UASs randomly distributed in a squared area at s; (Right) At s, the 50 UASs are flocking and have successfully formed a connected network.
For comparison purposes, two similar experiments were performed, but using the flocking algorithm introduced in [3], and Multirobot Cooperative Learning for Predator Avoidance (MCLPA) flocking algorithm introduced in [36] instead of the proposed algorithm. Figure 7 shows the velocities of all UASs on the x- and y-axis for all methods in an obstacle-free environment under the influence of the networked-induced delay. The plot shows that, although the delay is deterministic, it is unknown and the proposed method could effectively handle the influences of the network-induced delay.
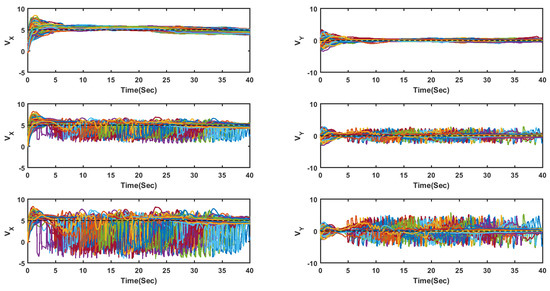
Figure 7.
Velocities of all UASs on the x and y-axis for all methods in an obstacle-free environment under the influence of the networked-induced delay. The proposed method top row, the MCLPA [36] middle row, and the flocking algorithm proposed in [3] the bottom row.
Figure 8 shows the Mean Square Error of the velocities of the overall group of agents, for the flocking methods in [3], the MCLPA flocking strategy in [36], and the BELBIC-based flocking, when evolving in an obstacle-free environment.
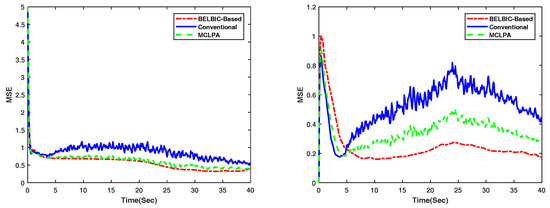
Figure 8.
Mean Square value of the velocities of all UAVs on the x-axis–(Left) and y-axis–(Right) generated by the overall group of agents when flocking in an obstacle-free environment. The BELBIC-based flocking is presented in dot-dashed red, the MCLPA flocking strategy in [36] in dashed green, and the flocking in [3] in solid blue. Notice that the MSE of the BELBIC-based flocking are smaller, and therefore more appropriate to implement in real-robots.
Table 2 shows the characteristics of the MSE of velocities of all flocking strategies for UAVs in the obstacle-free environment.

Table 2.
Characteristics of the MSE of all flocking strategies for UAVs in the obstacle-free environment.
5. Conclusions
The challenges of network-induced delay in flocking of networked multi-unmanned aircraft systems have been studied in this paper. A biologically-inspired distributed intelligent control methodology based on the emotional learning phenomenon in the mammalian limbic system has been proposed to overcome these challenges. Considering the influence of network-induced delay in real-time networked multi-unmanned aircraft systems flocking, the proposed technique demonstrated to be a promising tool for practical implementation because of its learning capability and low computational complexity. Computer-based numerical results of the implementation of the proposed methodology show the effectiveness of this algorithm for distributed intelligent flocking control of networked multi-UAS.
Future work will consider the implementation of a biologically-inspired intelligent control strategy for addressing real-world scenarios such as tracking, search and rescue, underwater explorations, etc.
Author Contributions
Conceptualization, M.J.; Methodology, M.J.; Software, M.J.; Validation, M.J. and H.X.; Formal Analysis, M.J.; Investigation, M.J.; Resources, M.J. and H.X.; Data Curation, M.J.; Writing-Original Draft Preparation, M.J.; Writing-Review & Editing, M.J. and H.X.; Visualization, M.J.; Supervision, H.X.; Project Administration, M.J. and H.X.; Funding Acquisition, H.X.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Appendix A.
Appendix A.1. Non-Adapting Phase
Our goal is to investigate the output of the system in non-adapting phase (i.e., when the system completes its learning process) so the Equations (10) and (11) which are the updating rules of Amygdala and Orbitofrontal Cortex, respectively, should be taken into consideration. In addition, we make an assumption that the function in Equation (10) could be neglected. By substituting (8) and (9) in Equation (7), the output of the model could be defined as follows:
When the learning process is completed (i.e., after system completes its learning process), the variations of the weights of Amygdala () and Orbitofrontal Cortex () will be equal to zero (i.e., ). With the assumption of the following holds:
Appendix A.2. Main Proof
Considering the results obtained in Subsection A.1, the following should be achieved:
Let us consider that is the weight of Amygdala for each control input l when the system has been learned and let be the Emotional Signal for each control input l during the adaptation phase. The following hold:
We will investigate the results of the following two cases:
- I.
- II.
Considering case I, the proof can be achieved as follows:
where ,
Considering case II, it is obvious that, when the max function in Equation (A9) will force the adaptation in the Amygdala to stop and the following hold:
The proof can be achieved as follows:
where and .
Appendix B.
Let’s consider that is a stable controller for the following system:
There is a Lyapunov function that guarantees the stability of the whole system:
Taking the first derivative, we have:
To provide the stability analysis of the actual system, let’s consider that the is an actual controller for the following system:
where is as follows:
and is the controller, which is given by the BELBIC model output . Considering the Lyapunov function , the following is obtained:
Taking the first derivative, we have:
Considering the Lyapunov function , the stability proof of overall system is as follows:
Taking the first derivative, we have:
References
- Reynolds, C.W. Flocks, herds and schools: A distributed behavioral model. ACM SIGGRAPH Comput. Graph. 1987, 21, 25–34. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Murray, R.M. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- Olfati-Saber, R. Flocking for multi-agent dynamic systems: Algorithms and theory. IEEE Trans. Autom. Control 2006, 51, 401–420. [Google Scholar] [CrossRef]
- Liu, B.; Yu, H. Flocking in multi-agent systems with a bounded control input. In Proceedings of the 2009 IWCFTA’09. International Workshop on IEEE Chaos-Fractals Theories and Applications, Los Alamitos, CA, USA, 6–8 November 2009; pp. 130–134. [Google Scholar]
- Jafari, M. On the Cooperative Control and Obstacle Avoidance of Multi-Vehicle Systems. Master’s Thesis, University of Nevada, Reno, NV, USA, 2015. [Google Scholar]
- Xu, H.; Carrillo, L.R.G. Distributed near optimal flocking control for multiple Unmanned Aircraft Systems. In Proceedings of the IEEE 2015 International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; pp. 879–885. [Google Scholar]
- Jafari, M.; Sengupta, S.; La, H.M. Adaptive flocking control of multiple unmanned ground vehicles by using a uav. In Proceedings of the International Symposium on Visual Computing, Las Vegas, NV, USA, 14–16 December 2015; pp. 628–637. [Google Scholar]
- O’Loan, O.; Evans, M. Alternating steady state in one-dimensional flocking. J. Phys. A Math. Gen. 1999, 32, L99. [Google Scholar] [CrossRef]
- Li, S.; Liu, X.; Tang, W.; Zhang, J. Flocking of Multi-Agents Following a Leader with Adaptive Protocol in a Noisy Environment. Asian J. Control 2014, 16, 1771–1778. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, P.; Yang, Z.; Chen, Z. Adaptive flocking of non-linear multi-agents systems with uncertain parameters. IET Control Theory Appl. 2014, 9, 351–357. [Google Scholar] [CrossRef]
- Dong, Y.; Huang, J. Flocking with connectivity preservation of multiple double integrator systems subject to external disturbances by a distributed control law. Automatica 2015, 55, 197–203. [Google Scholar] [CrossRef]
- Jafari, M.; Xu, H.; Carrillo, L.R.G. Brain Emotional Learning-Based Intelligent Controller for flocking of Multi-Agent Systems. In Proceedings of the 2017 IEEE American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 1996–2001. [Google Scholar]
- Chopra, N.; Spong, M.W. Output synchronization of nonlinear systems with time delay in communication. In Proceedings of the 2006 45th IEEE Conference on IEEE, Decision and Control, Sydney, Australia, 13–15 December 2006; pp. 4986–4992. [Google Scholar]
- Nourmohammadi, A.; Jafari, M.; Zander, T.O. A Survey on Unmanned Aerial Vehicle Remote Control Using Brain–Computer Interface. IEEE Trans. Hum. Mach. Syst. 2018, 48, 337–348. [Google Scholar] [CrossRef]
- Wan, Z. Flocking for Multi-Agent Dynamical Systems. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2012. [Google Scholar]
- Yang, Z.; Zhang, Q.; Jiang, Z.; Chen, Z. Flocking of multi-agents with time delay. Int. J. Syst. Sci. 2012, 43, 2125–2134. [Google Scholar] [CrossRef]
- Liu, Y.; Ho, D.W.; Wang, Z. A new framework for consensus for discrete-time directed networks of multi-agents with distributed delays. Int. J. Control 2012, 85, 1755–1765. [Google Scholar] [CrossRef]
- Kar, S.; Moura, J.M. Distributed consensus algorithms in sensor networks with imperfect communication: Link failures and channel noise. IEEE Trans. Signal Process. 2009, 57, 355–369. [Google Scholar] [CrossRef]
- Mehrabian, A.R.; Khorasani, K. Distributed formation recovery control of heterogeneous multiagent euler–lagrange systems subject to network switching and diagnostic imperfections. IEEE Trans. Control Syst. Technol. 2016, 24, 2158–2166. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, P.; Yang, Z.; Chen, Z. Distance constrained based adaptive flocking control for multiagent networks with time delay. Math. Probl. Eng. 2015, 2015. [Google Scholar] [CrossRef]
- Cao, Y.; Oguchi, T. Coordinated Control of Mobile Robots with Delay Compensation Based on Synchronization. In Sensing and Control for Autonomous Vehicles; Springer: Berlin, Germany, 2017; pp. 495–514. [Google Scholar]
- Dashti, Z.A.S.; Gholami, M.; Jafari, M.; Shoorehdeli, M.A.; Teshnehlab, M. Speed control of a Digital Servo System using parallel distributed compensation controller and Neural Adaptive controller. In Proceedings of the 2013 13th Iranian Conference on IEEE, Fuzzy Systems (IFSC), Qazvin, Iran, 27–29 August 2013; pp. 1–6. [Google Scholar]
- Jafari, M.; Xu, H.; Garcia Carrillo, L.R. A neurobiologically-inspired intelligent trajectory tracking control for unmanned aircraft systems with uncertain system dynamics and disturbance. Trans. Inst. Meas. Control 2018. [Google Scholar] [CrossRef]
- Jafari, M.; Sarfi, V.; Ghasemkhani, A.; Livani, H.; Yang, L.; Xu, H.; Koosha, R. Adaptive neural network based intelligent secondary control for microgrids. In Proceedings of the 2018 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 8–9 February 2018; pp. 1–6. [Google Scholar]
- Moren, J.; Balkenius, C. A computational model of emotional learning in the amygdala. Anim. Anim. 2000, 6, 115–124. [Google Scholar]
- Lucas, C.; Shahmirzadi, D.; Sheikholeslami, N. Introducing BELBIC: brain emotional learning based intelligent controller. Intell. Autom. Soft Comput. 2004, 10, 11–21. [Google Scholar] [CrossRef]
- Kim, J.W.; Oh, C.Y.; Chung, J.W.; Kim, K.H. Brain emotional limbic-based intelligent controller design for control of a haptic device. Int. J. Autom. Control 2017, 11, 358–371. [Google Scholar] [CrossRef]
- Rizzi, C.; Johnson, C.G.; Fabris, F.; Vargas, P.A. A situation-aware fear learning (SAFEL) model for robots. Neurocomputing 2017, 221, 32–47. [Google Scholar] [CrossRef]
- Jafari, M.; Xu, H. A Biologically-Inspired Distributed Intelligent Flocking Control for Networked Multi-UAS with Uncertain Network Imperfections. In Proceedings of the 2018 International Conference on Unmanned Aircraft Systems (ICUAS), Dallas, TX, USA, 12–15 June 2018; pp. 12–21. [Google Scholar]
- Jafari, M.; Xu, H. Intelligent Control for Unmanned Aerial Systems with System Uncertainties and Disturbances Using Artificial Neural Network. Drones 2018, 2, 30. [Google Scholar] [CrossRef]
- Jafari, M.; Shahri, A.M.; Shouraki, S.B. Attitude control of a quadrotor using brain emotional learning based intelligent controller. In Proceedings of the 2013 13th Iranian Conference on IEEE, Fuzzy Systems (IFSC), Qazvin, Iran, 27–29 August 2013; pp. 1–5. [Google Scholar]
- Jafari, M.; Shahri, A.M.; Elyas, S.H. Optimal Tuning of Brain Emotional Learning Based Intelligent Controller Using Clonal Selection Algorithm. In Proceedings of the 2013 3th International eConference on IEEE, Computer and Knowledge Engineering (ICCKE), Mashhad, Iran, 31 October–1 November 2013; pp. 30–34. [Google Scholar]
- Lin, C.M.; Chung, C.C. Fuzzy Brain Emotional Learning Control System Design for Nonlinear Systems. Int. J. Fuzzy Syst. 2015, 17, 117–128. [Google Scholar] [CrossRef]
- Mei, Y.; Tan, G.; Liu, Z. An improved brain-inspired emotional learning algorithm for fast classification. Algorithms 2017, 10, 70. [Google Scholar] [CrossRef]
- El-Garhy, M.A.A.A.; Mubarak, R.; El-Bably, M. Improving maximum power point tracking of partially shaded photovoltaic system by using IPSO-BELBIC. J. Instrum. 2017, 12, P08012. [Google Scholar] [CrossRef]
- La, H.M.; Lim, R.; Sheng, W. Multirobot cooperative learning for predator avoidance. IEEE Trans. Control Syst. Technol. 2015, 23, 52–63. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).