1. Introduction
1.1. Motivation
Unmanned Aircraft Systems (UAS) are widely being employed in various applications due to their vast functionality and the recent advances in the technology. Their wide range of applications include but not limited to search and rescue, wind turbine inspection, reconnaissance and mapping, target tracking, environmental monitoring, etc. [
1,
2,
3,
4,
5,
6,
7]. Quad rotorcraft is one of the most flexible UAS platforms with hovering and Vertical Takeoff and Landing (VTOL) capabilities [
1,
8]. Due to their unprecedented role in performing aerial operations, UAS attract tremendous interests from different research communities. Specifically, designing control methodologies for UAS requires rigorous consideration, due to their inherently unstable nature, system dynamics uncertainties and also the existence of the environmental disturbances.
Reviewing the related works in the UAS control scheme shows that most of the state-of-the-art methods require detailed information about the system (i.e., the UAS dynamics). Considering the facts that the dynamics of UAS are nonlinear and complex, and also there are uncertainties imposed to the system, such as system dynamics uncertainties and noise/disturbances, the development of a model-free adaptive intelligent controller becomes a paramount importance. Furthermore, when dealing with real-time systems, in addition to handling the model uncertainties, diverse issues such as instability of the system during the online training of the learning based control techniques might arise. For this reason, the development of control strategies with less dependency on the full knowledge of the system dynamics and also ensuring the reliable online training phase is critical for successfully accomplishing the robot’s mission.
1.2. Related Works
To overcome the challenges of controlling the UAS, diverse control schemes have been proposed. For example, a reinforcement learning based methodology was proposed by authors in [
9] to stabilize a quad rotorcraft. The authors in [
10] investigated the stabilization of a quad rotorcraft during flight by employing an adaptive fuzzy logic controller. Closely related, the development of an adaptive sliding mode control approach was studied by the authors in [
11] for controlling the flight of the UAS. In addition, an adaptive neural network based controller has been proposed in [
12]. Recently, the authors in [
13] used a quaternion representation for developing a nonlinear robust output feedback tracking control for a UAS. Moreover, neural network based nonlinear model reference adaptive controller has been proposed in [
14] for controlling a UAS. More recently, designing a neuro-fuzzy controller for attitude-tracking stabilization of a multi-rotor UAS is investigated in [
15]. Furthermore, a robust attitude control of a miniature quad rotorcraft was addressed by the authors in [
16]. Despite the advantages of these previous methodologies, to be successfully implemented, most of these state-of-the-art works require detailed information about the system (i.e., the UAS dynamics). Besides, the dependency on the UAS dynamics, the learning based control techniques did not fully consider the occurrence of the instability of the system during their online training phase. In this regard, the development of control strategies with less dependency on the full knowledge of the system dynamics and with reliable online training phase is essential. In recent years, learning based approaches have been extensively utilized for successfully solving diverse complex problems [
17,
18,
19,
20,
21]. From a control system point of view, neural network based approaches are effective when the system dynamics are fully or partially unknown. Furthermore, the developed controller should ensure the stability of the system during its online training phase and effectively compensate the system performance when there are disturbances occurring in the system.
1.3. Main Contributions
The main objective of this paper is to develop an adaptive intelligent control for stabilization of a quad rotorcraft with system uncertainties and disturbances. To accomplish this objective, we propose an adaptive neural network (NN) based intelligent controller, which utilizes a neural network based identifier and a neural network based controller. The parameters of the NN-based controller are designed based on both the identified model of the system and the linear controller. A modulator block is utilized for generating a smooth transition between the linear controller and NN-based controller, according to the system states to ensure the stability of the system during its online training phase. Whenever the NN-based controller is in the training phase, the linear controller is activated to keep the system states in a safe region. Therefore, this control architecture could be employed for real-time operation. The learning capability of the proposed approach is validated for stabilizing a quad rotorcraft with promising performance. Furthermore, the robustness of the proposed controller with respect to variations in system parameters has been demonstrated through different simulations.
In other words, the solution proposed in this paper is an adaptive neural network (NN) based intelligent controller, which provides the following benefits:
The knowledge of system dynamics is not fully or partially required.
It has the capabilities of uncertainty handling and noise/disturbance rejection (i.e., adding a neural network based identifier in parallel with the system, provides the capability of handling the uncertainties and disturbances of the system).
It is appropriate for real-time implementation due to its low computational complexity (i.e., the developed algorithm is a real-time applicable learning technique).
It Ensures the stability of the system during its online training phase (i.e, the linear and/or nonlinear controller is utilized, therefore, the system states will be kept in a safe region where the neural network could be accurately pass the training phase and achieve the optimal control).
The rest of the paper is organized as follows.
Section 2 presents the problem statement. Our main contribution is introduced in
Section 3, which consists of neural network based intelligent control of a quad rotorcraft.
Section 4 presents numerical simulation results. The conclusion and future directions of our work are provided in
Section 5.
2. Problem Formulation and Preliminaries
Consider the real-time autonomous flight of a UAS. Consider also the facts that the dynamics of the UAS are nonlinear and complex, and there are uncertainties imposed to the system, such as system dynamics uncertainties and noise/disturbances. The main objective of this research consists on the design of an adaptive intelligent control strategy, which is effective for the real-time autonomous flight of a UAS, even under the system uncertainties and disturbances. The details of the proposed approach are explained in the following subsections.
2.1. UAS Dynamics Representation
Considering a hybrid system of coordinates, i.e., H-frame [
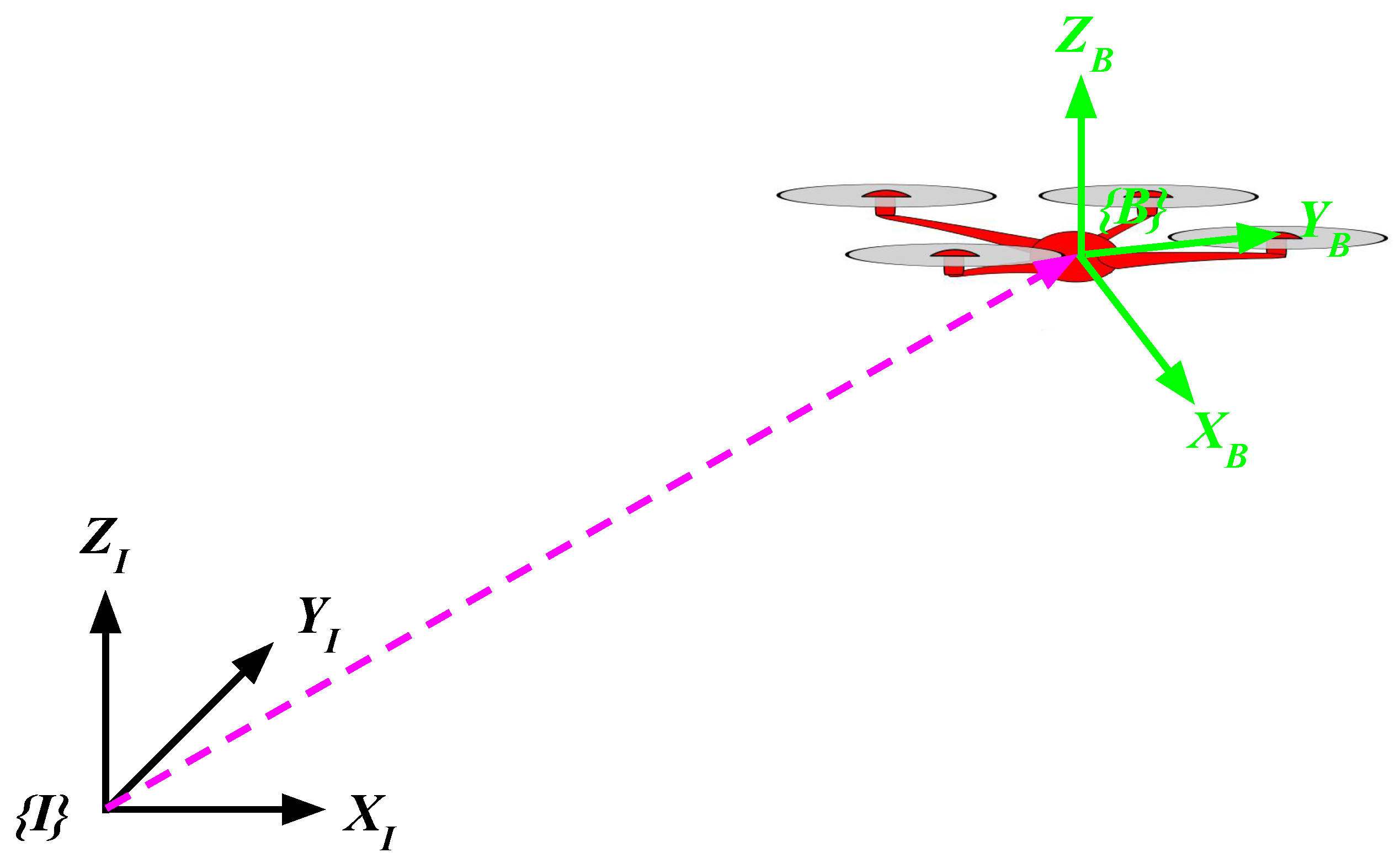
22], the dynamics of the UAS are described in this subsection to analytically validating the proposed controller. This system is composed of a set of angular equations with respect to (w.r.t.) a body fixed frame (B-frame) and a set of nonlinear equations w.r.t. an inertial frame (I-frame), see
Figure 1. A set of UAS nonlinear equations w.r.t. the H-frame is described as follows [
22]:
where all the parameters of Equation (
1) are defined in
Table 1.
Additionally, the propellers’ speed are related to the moments as follows:
where all the parameters of Equation (
2) are defined in
Table 1.
Ultimately, the nonlinearities of the quad rotorcraft motors is described as follows:
where all the parameters of Equation (3) are defined in
Table 1.
2.2. Neural Network Based Control
Neural network based approaches have been extensively applied in the control and identification of dynamic systems [
18]. There are different classes of artificial neural networks (ANN), such as multilayer perceptron (MLP), radial basis function (RBF) network, Hopfield network, etc. [
23], in which RBF has the capabilities of the local specialization and the global generalization [
24]. RBF has also the capability of acting as a universal approximator which is promising for identification and controlling the dynamic systems [
24]. A radial basis function (RBF) network is a type of artificial neural network that utilizes the radial basis functions as its activation functions. Radial basis function is a type of radially symmetric functions which their values only depend on the distance from a center vector (i.e.,
). In general, the norm (i.e.,
) is defined by the Euclidean distance and the radial basis function is considered as a Gaussian function:
In general, the RBF networks consist of three layers: (i) an input layer; (ii) a hidden layer with a nonlinear RBF activation function; and (iii) a linear output layer. In this paper, for each controller, an RBF network is designed where the number of nodes in the input, and output layers are 5, and 1, respectively. The same configuration is used for the NN-based identifier. The number of the nodes in the hidden layer is not fixed. The RBF algorithm utilized in this work, creates neurons one at a time. The error of the new network is checked, and if low enough the RBF algorithm is finished. Otherwise, the next neuron is added. This procedure is repeated until the error goal is met or the maximum number of neurons is reached.
The input to an RBF network can be modeled as a vector of real numbers
. Then, the output of the RBF network, which is a scalar function of its input vector,
, can be defined by
where
,
, and
are the number of neurons in the hidden layer, the center vector for the
th neuron, and the weight of the
th neuron in the linear output neuron, respectively.
RBF networks has the capability of acting as the universal approximators on a compact subset of
[
24]. In other words, any continuous function on a closed, bounded set can be approximated by an RBF network with enough f neurons in its hidden layer. Furthermore, the learning and training time of RBF networks is faster in comparison with the MLP [
23]. Therefore, an RBF network is employed in the proposed method.
Neural Network Based Identification and Control
Neural network based control methods are effective when the system dynamics are fully or partially unknown. There are two general identification model: (i) Direct Model; and (ii) Inverse Model. The objective of the direct model is that the output of neural network identifier converges to the output of the actual system, while the objective of the inverse model is to design a neural network identifier which is equivalent to the inverse of the system. The inverse model is utilized in the control methodologies that requires inverse dynamic of the system. In general, one could categorize the adaptive neural network based control architectures in one of the following two categories:
Direct Control: When the dynamic model of the system is fully known, it is possible to directly adjust the parameters of the neural network based controller to reduce the output error of the system.
Indirect Control: When the dynamic model of the system is partially known or unknown, it is not possible to apply the above method (i.e., direct control method). Therefore, in indirect control method, the model of the dynamic system is identified first and then the parameters of the neural network based controller are defined based on the identified model of the system.
In
Section 3, a combination of identification and control techniques is deployed to design an adaptive neural network based controller for a quad rotorcraft. More detailed studies about neural network based control techniques can be found in [
18,
23].
2.3. Objectives
Based on the quad rotorcraft model described in
Section 2.1, and by leveraging the neural network control introduced in
Section 2.2, the objective is to design four control signals {
,
,
,
}, as an adaptive intelligent controller, for stabilizing the quad rotorcraft. Specifically, the proposed adaptive intelligent control method is designed to stabilize the quad rotorcraft in the events of disturbances.
3. Adaptive Intelligent Control of Quad Rotorcrafts Using Neural Network
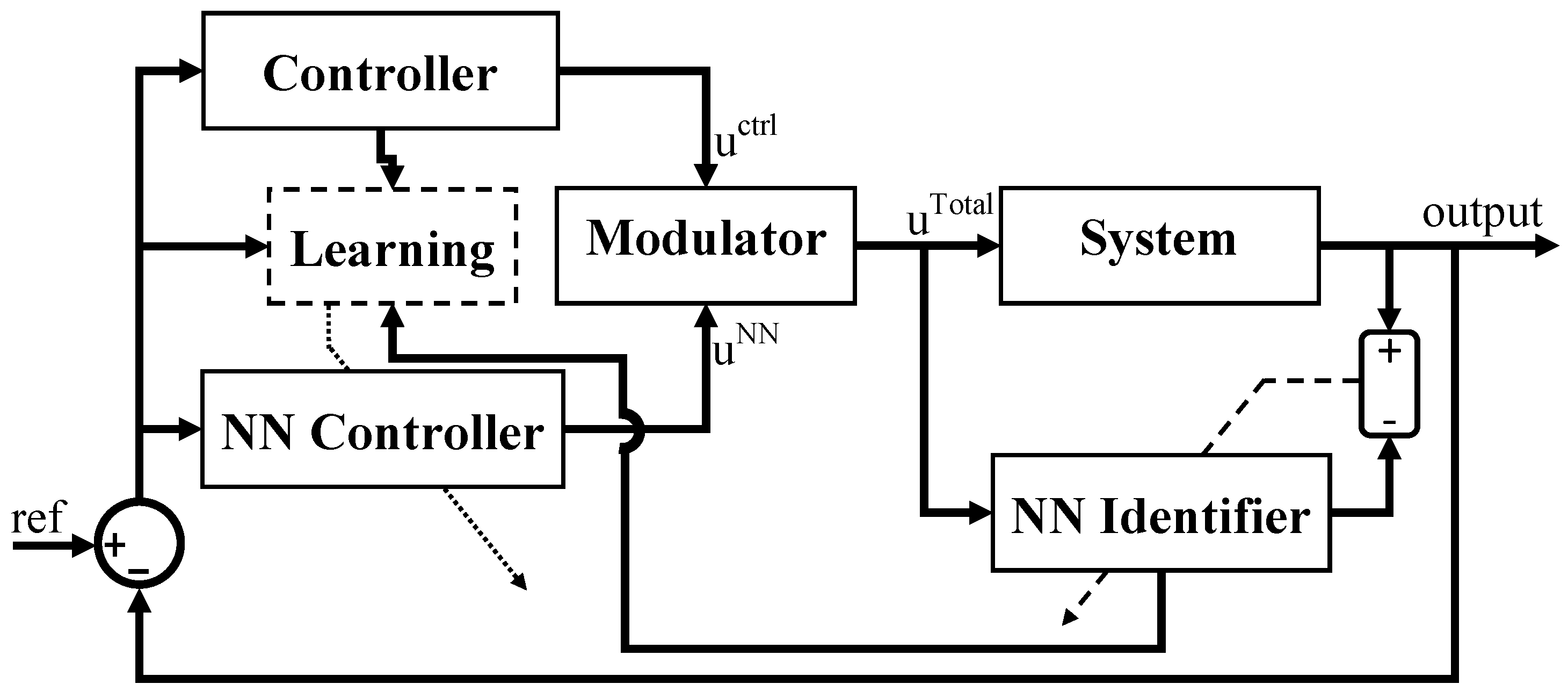
The neural network based control architecture is shown in
Figure 2. This model consists of a linear or nonlinear controller, an adaptive neural network controller, a modulator block, the system to be controlled, and a neural network identifier. The overall control signal (i.e.,
) is obtained as follows:
where
is the neural network controller output,
is the linear or nonlinear controller output,
is a smooth function and
i is the controller index. A possible smooth function (i.e.,
) is defined as follows:
where
,
, and
are different regions of system states. The modulator block operates in such a way to generate a smooth transition between the linear or nonlinear controller, and the adaptive neural network controller, according to the system states.
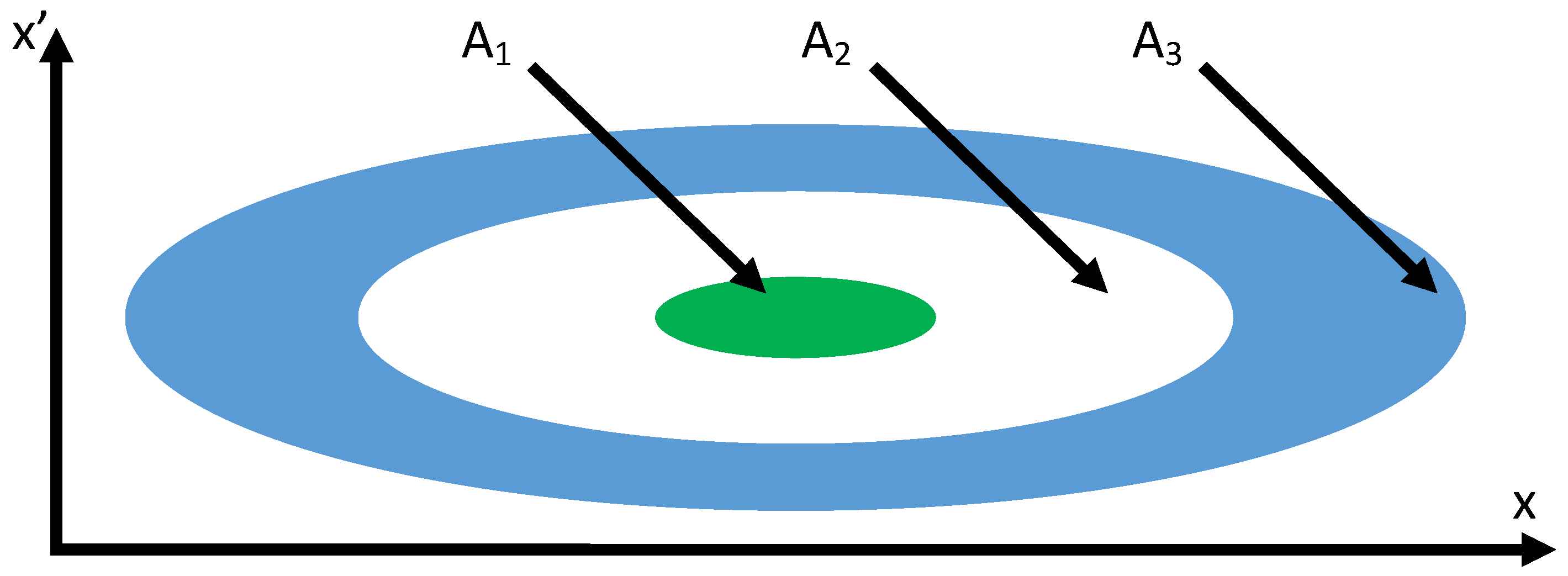
Figure 3 shows a possible assignment of these regions.
To keep the system states in a region (
in
Figure 3) where the neural network could accurately pass the training phase and achieve the optimal control (i.e., to ensure the stability of the system during its online training phase), a linear or nonlinear controller is utilized. Whenever the system states drift outside the aforementioned region (
and
in
Figure 3), the linear or nonlinear controller is activated (and the NN-controller is deactivated). The combination of these controllers develops a stable system. Furthermore, since there are uncertainties in the system dynamics, the identifier is also designed and deployed. Adding a neural network based identifier in parallel with the system provides the capability of handling the uncertainties and disturbances of the system. The NN-based identifier is trained to receive the same inputs as the system and to produce the same output. The difference between the outputs will be interpreted as the effect of the uncertainties and disturbances of the system. That signal will then enter to the learning algorithm of the NN-based controller. The proposed strategy will take care of the uncertainties and disturbances of the system. Then, the parameters of the neural network based controller are defined based on both the identified model of the system and linear or nonlinear controller. The RBF artificial neural networks are deployed for designing both identifier and controller. In this paper, the PID controller is used as a linear controller (i.e.,
) beside the NN-controller (i.e.,
). Equations (8) and (9) show these controllers, respectively.
where
,
, and
are the PID controller coefficients and
e is the system error.
,
, and
are the number of neurons in the hidden layer, the center vector for the
neuron, and the weight of the
neuron in the linear output neuron, respectively.
4. Simulation Results
This section presents the computer based numerical simulation results of the quad rotorcraft control under two different scenarios: intelligent NN-based control in wind-free environment, and intelligent NN-based control in presence of wind disturbance. In the first scenario, intelligent NN-based controller is utilized to generate control signals {,,,} for quad rotorcraft in the wind-free environment while, in the last scenario, intelligent NN-based controller is utilized to generate control signals {,,,} for quad rotorcraft in the presence of wind disturbance. In all scenarios, the total simulation time is 20 seconds. All simulations are carried out on a platform with following specifications: Windows Server 2012 R2 standard, Processor: Intel(R) Xeon(R) CPU E5-2680 0 @ 2.70 GHz (4 processors), RAM: 8.00 GB.
Generally, the configuration of the NN differs for different problems [
18]. In this paper, for each controller, an RBF network is designed where the number of nodes in the input, and output layers are 5, and 1, respectively. The same configuration is used for the NN-based identifier. In most cases,
of datasets is used for training,
for validation, and
for testing [
18]. However, in this paper, the parameters of the NN-based controller are defined based on both the identified model of the system and linear or nonlinear controller, therefore, the offline training phase is not needed. Ultimately, whenever the NN-based controller is in the training phase, the linear or nonlinear controller is activated to keep the system states in a safe region. Therefore, this control architecture could operate online and the calculation of the updating rate for the NN-based controller is not critical.
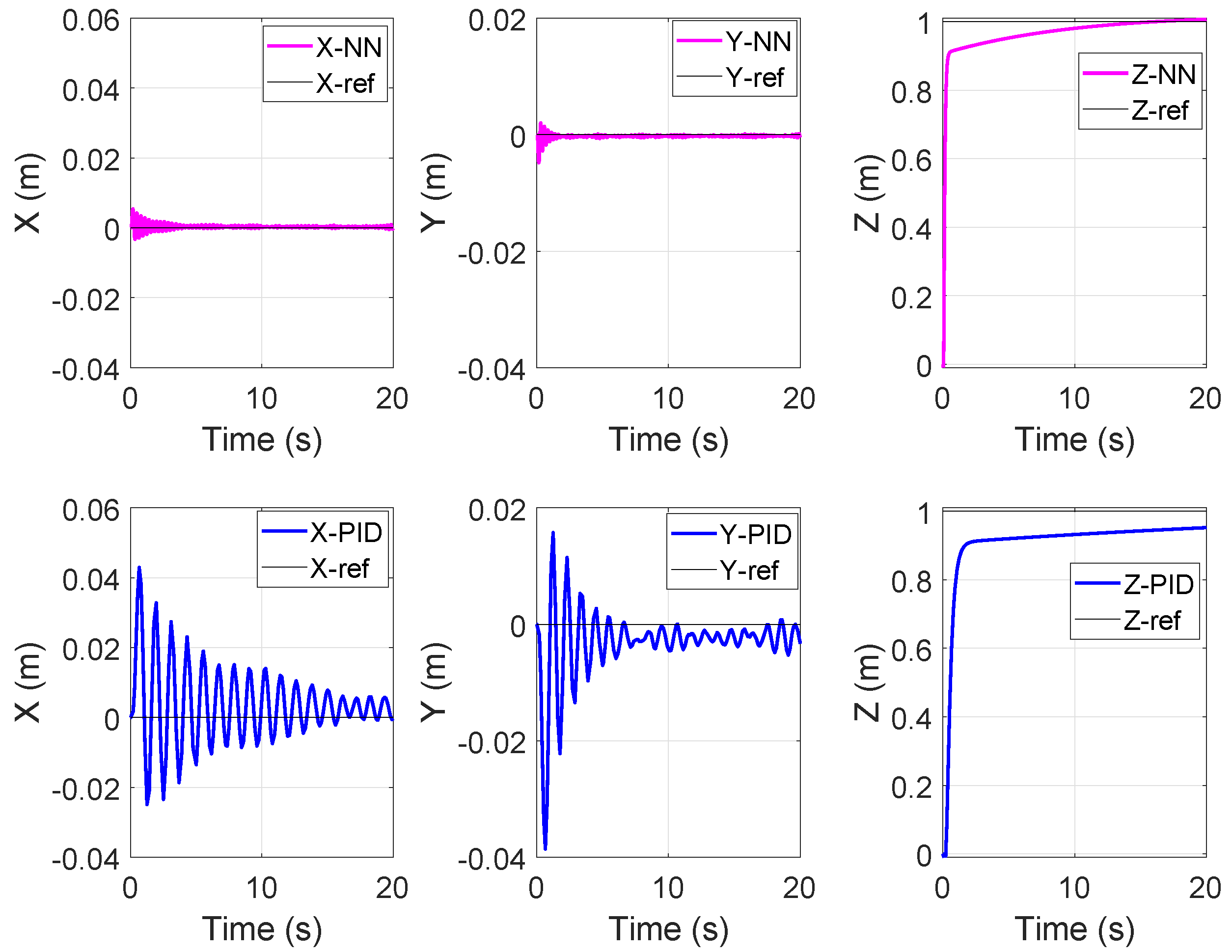
In the first examination, Vertical Take off of the Quadcopter is investigated. The flight should reach to 1 m heights.
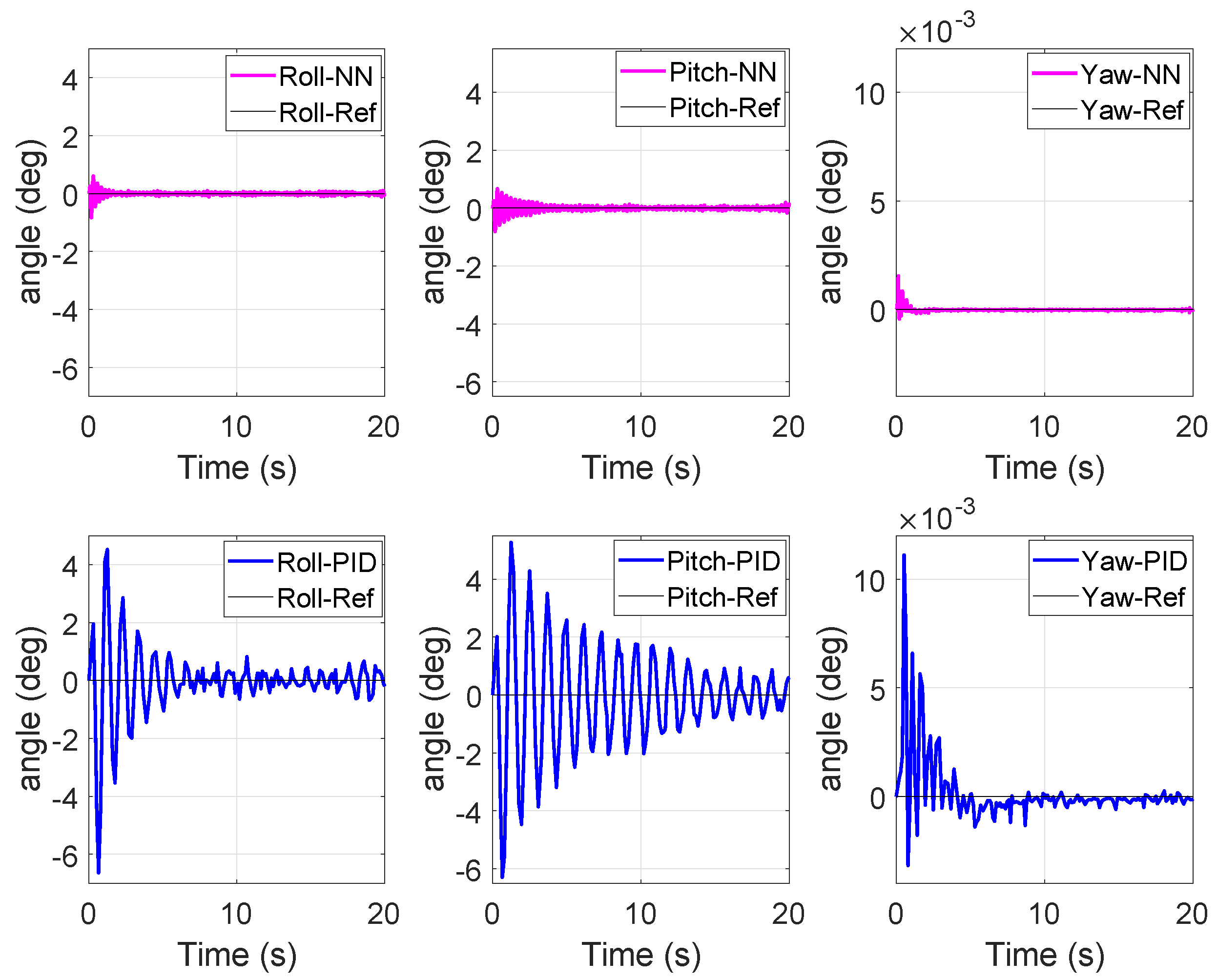
Figure 4 and
Figure 5 (top, magenta) show the attitude control of the model without any disturbance using NN-based controller while
Figure 4 and
Figure 5 (bottom, blue) show the attitude control of the model without any disturbance using PID controller. From these plots, it is observed that both PID and the proposed NN-controller methods are capable of stabilizing the system. However, the proposed controller has faster response, lower overshoot, and smaller settling time in comparison with the PID controller.
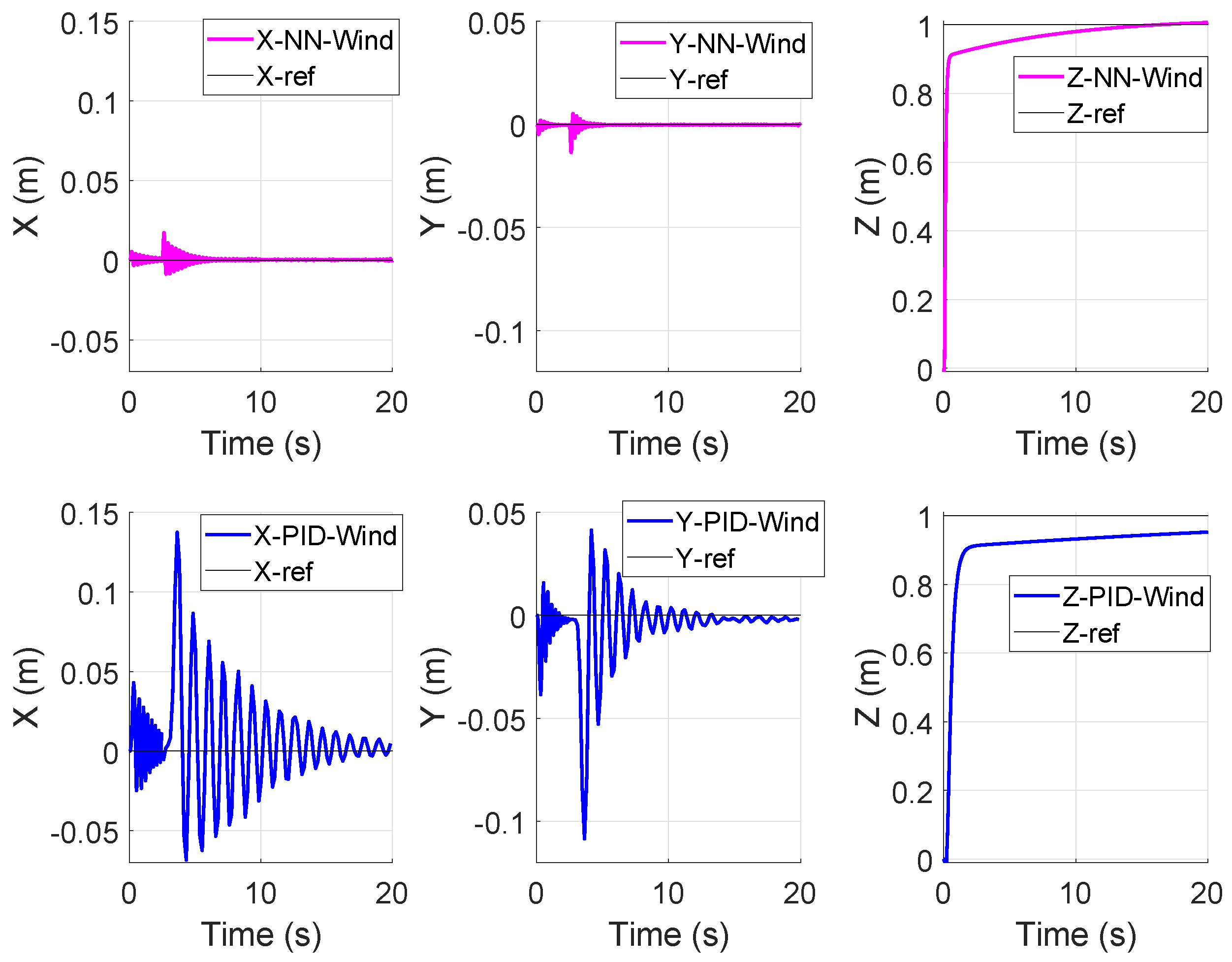
Aerodynamically, a side wind acting on a spinning propeller induces a side force, pitching moment, yawing moment and an increase in thrust. The side force and pitching moment have the most significant impact on the motion of a Quadcopter [
25]. Here, to investigate the effect of the wind, a force of 1 (N.m) is applied to pitch angle starting at t = 2.5 s.
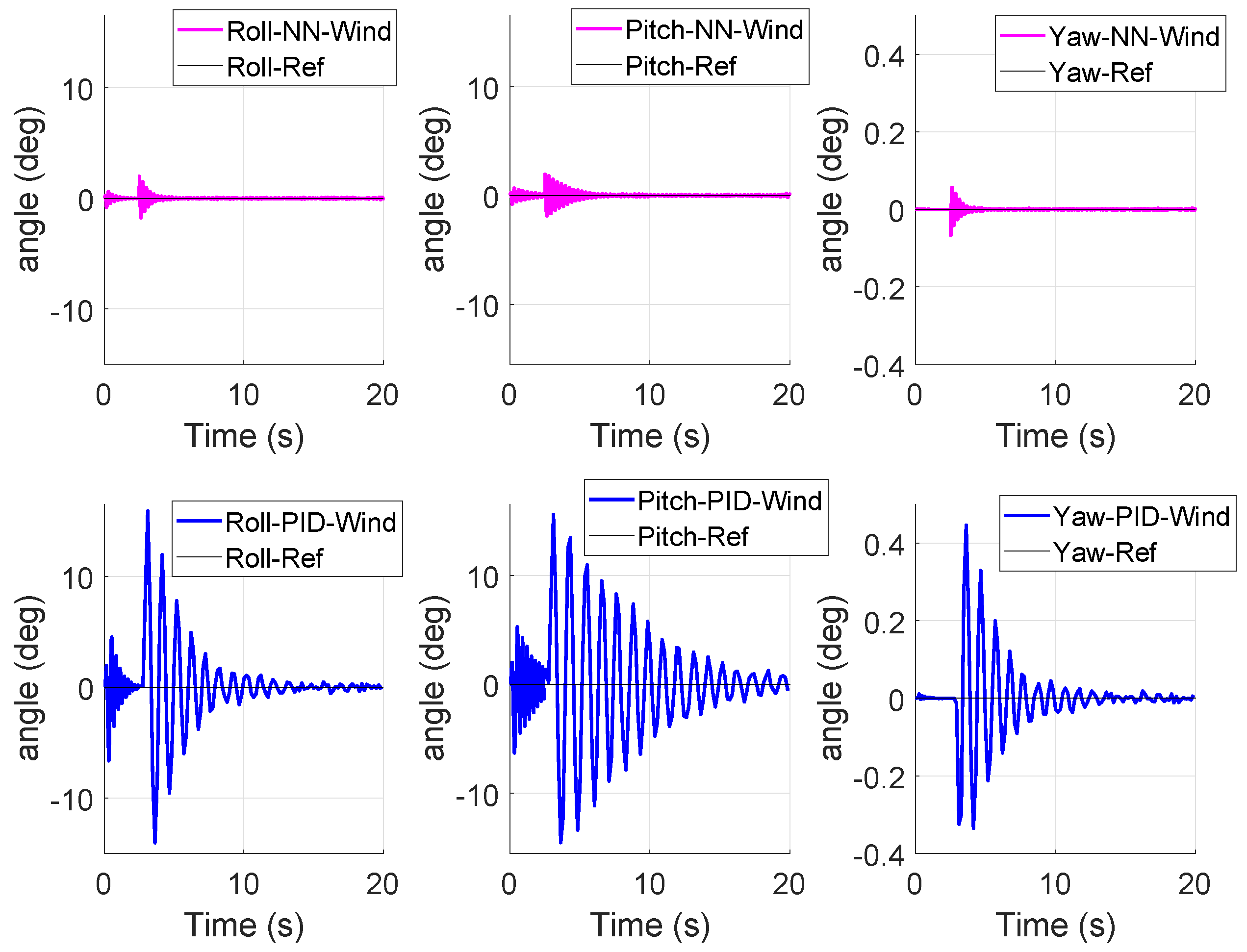
Figure 6 and
Figure 7 (top, magenta) plot the attitude control of the Quadcopter in presence of wind using NN-based controller while
Figure 6 and
Figure 7 (bottom, blue) plot the attitude control of the Quadcopter in presence of wind using PID controller. From these plots, it is observed that both PID and the proposed NN-controller methods are capable of handling the disturbance. However, the proposed controller responds faster than the PID controller to successfully handle the disturbance in the system. Therefore, it is appropriate for controlling the quad rotorcraft.
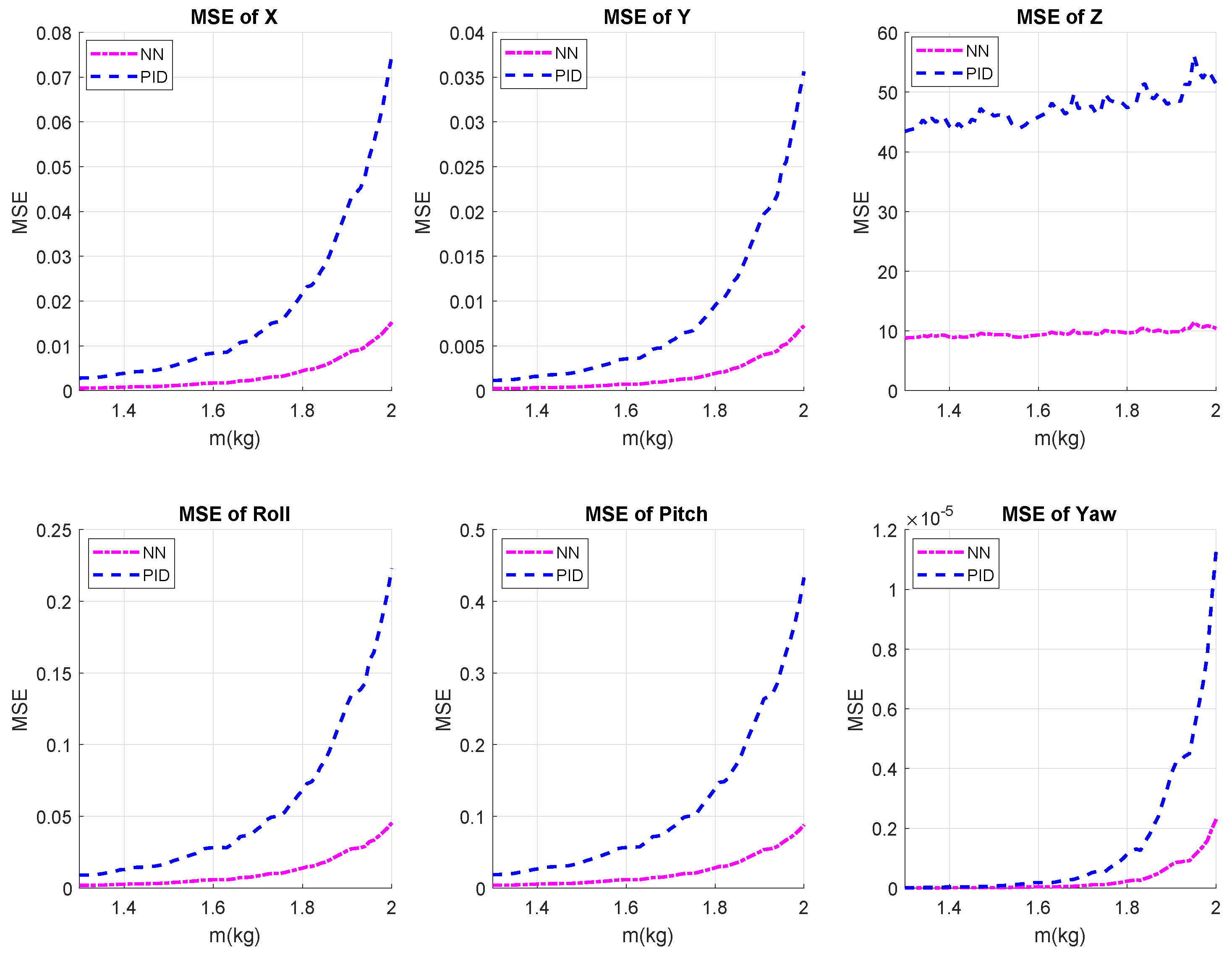
Aside from faults and/or disturbances, the dynamic of the system might be fully or partially unknown and, even after employing identification methods, the characteristics of the system might change due to wear and tear, environmental changes, etc. Therefore, different simulations have been done to study the sensitivity of both controllers with respect to variations in system parameters such as: UAS mass (
m). The objective is to evaluate the performance of both controllers, considering that their settings remain the same as before. In other words, there was no additional tuning of the controllers for adapting to the new system parameters.
Figure 8 shows the Mean Square Error (MSE) of the
x,
y, and
z positions and roll, pitch, and yaw angles for both controllers considering the different values for UAS mass (
m). This figure demonstrate that the proposed method has both less MSE and small variation due to the changing of system parameters. Therefore, it is more robust and appropriate for controlling the UAS.
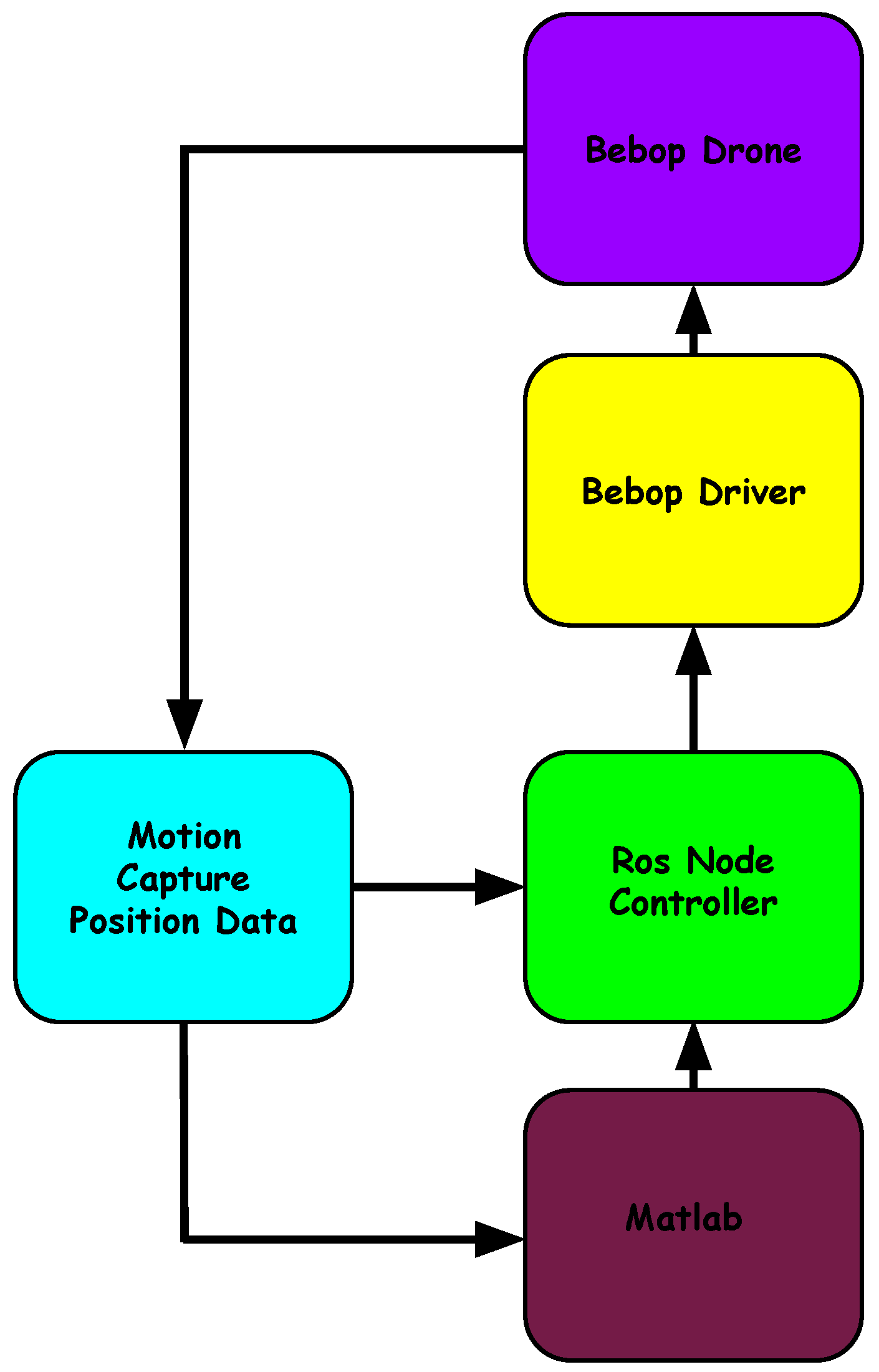
Experimental Testbed
The platform implemented for future validation of the proposed algorithm is available at the Unmanned Systems Laboratory (USL) from the University of Nevada, Reno. The Base Station of this testbed runs Ubuntu 14.04 OS, the Robot Operating System (ROS) environment, and Matlab. The UAV platform corresponds to a Bebop drone manufactured by Parrot.
The three-dimensional position of the UAV is obtained by means of a Motion Capture System (MCS) manufactured by OptiTrack. The information provided by the MCS is reported to the OptiTrack Interface PC by means of a Gigabyte Ethernet connection. Next, this information is sent to the Base Station PC by means of an Ethernet connection. The Base Station computer uses this information to execute the adaptive neural network based intelligent control algorithm and to calculate four control signals {
,
,
,
}, which are sent to the Bebop platform by means of a WiFi link.
Figure 9 and
Figure 10 show the experimental testbed and the proposed dataflow which will be used for future evaluation of the proposed algorithm on a Bebop drone.