Adaptive Edge Intelligent Joint Optimization of UAV Computation Offloading and Trajectory Under Time-Varying Channels

Highlights

What are the main findings?

• The proposed Adaptive UAV Edge Intelligence Framework (AUEIF) effectively decouples the complexities of UAV trajectory, computation offloading, and dynamic air-to-ground communication, significantly improving adaptability and efficiency in multi-UAV MEC systems.
• A hierarchical reinforcement learning (HRL) approach optimizes large-scale action spaces by combining high-level trajectory control with fine-grained offloading and resource allocation, enabling scalable and adaptive decisionmaking across different time scales.

What are the implications of the main findings?

• The AUEIF demonstrates superior performance in task latency reduction and energy efficiency compared to conventional methods, with enhanced robustness under severe channel fading conditions, supporting reliable real-world UAV deployment.
• The integration of dynamic modeling, predictive LSTM-based channel forecasting, and hierarchical learning offers a modular and scalable blueprint for next-generation adaptive MEC systems capable of operating in highly dynamic environments.

Abstract

With the rapid development of mobile edge computing (MEC) and unmanned aerial vehicle (UAV) communication networks, UAV-assisted edge computing has emerged as a promising paradigm for low-latency and energy-efficient computation. However, the time-varying nature of air-to-ground channels and the coupling between UAV trajectories and computation offloading decisions significantly increase system complexity. To address these challenges, this paper proposes an Adaptive UAV Edge Intelligence Framework (AUEIF) for joint UAV computation offloading and trajectory optimization under dynamic channels. Specifically, a dynamic graph-based system model is constructed to characterize the spatio-temporal correlation between UAV motion and channel variations. A hierarchical reinforcement learning-based optimization framework is developed, in which a high-level actor–critic module is responsible for generating coarse-grained UAV flight trajectories, while a low-level deep Q-network performs fine-grained optimization of task offloading ratios and computational resource allocation in real time. In addition, an adaptive channel prediction module leveraging long short-term memory (LSTM) networks is integrated to model temporal channel state transitions and to assist policy learning and updates. Extensive simulation results demonstrate that the proposed AUEIF achieves significant improvements in end-to-end latency, energy efficiency, and overall system stability compared with conventional deep reinforcement learning approaches and heuristic-based schemes while exhibiting strong robustness against dynamic and fluctuating wireless channel conditions.

1. Introduction

With the rapid advancement of mobile edge computing (MEC) and unmanned aerial vehicle (UAV) communications, UAV-assisted MEC has emerged as a promising paradigm for delivering low-latency and energy-efficient computing services to mobile users (MUs), particularly in areas with limited terrestrial infrastructure or unreliable network coverage [1,2,3]. Unlike conventional fixed MEC servers, UAVs possess high mobility and flexible deployment capabilities, enabling dynamic trajectory adjustment in response to spatio-temporal variations in user distribution, task generation, and wireless channel conditions, thereby enhancing service adaptability and resilience [4]. Nevertheless, UAV-assisted MEC faces significant challenges due to the highly dynamic air-to-ground (A2G) channels, which induce strong coupling between UAV mobility, task offloading decisions, and resource allocation. Many existing solutions inadequately capture the spatio-temporal correlations among these tightly interdependent components. Moreover, the high-dimensional decision space and complex system dynamics often lead to excessive computational complexity and slow convergence, hindering real-time adaptability in multi-UAV environments [5].

To address the above challenges, extensive research efforts have investigated optimization-based approaches for UAV-assisted MEC systems, primarily focusing on joint UAV trajectory planning and task offloading design. Yang et al. [6] proposed a perturbation-based Lyapunov optimization (PLOT) framework for energy-harvesting UAV-MEC systems, which transforms long-term stochastic optimization problems into per-slot deterministic subproblems. Hao et al. [7] developed a reliability-aware offloading framework by integrating perceptual representation with TD3-based deep reinforcement learning to maximize long-term task success probability. Nguyen et al. [8] studied joint partial offloading, UAV trajectory control, edge–cloud computation, and radio resource allocation in space–air–ground integrated networks, demonstrating notable improvements in energy efficiency. Similarly, Zhang et al. [9] employed convex optimization techniques to minimize average response delay through joint UAV deployment, user association, and task offloading strategies. Xu et al. [10] formulated a weighted computation efficiency maximization problem with aerial–ground cooperation, jointly optimizing task allocation, bandwidth assignment, CPU frequency, and UAV trajectory to balance computation performance and energy consumption.

To cope with the high-dimensional state and action spaces as well as the dynamic nature of UAV-MEC systems, learning-based and multi-agent approaches have attracted increasing attention. Zhao et al. [11] proposed a multi-agent deep reinforcement learning (MADRL) framework to jointly optimize UAV trajectories, task allocation, and communication resources, enabling scalable control in continuous action spaces. Chen et al. [12] developed a hybrid nature-inspired optimization scheme for joint UAV positioning, task offloading, and resource allocation. Al-Bakhrani et al. [13] introduced a multi-objective adaptive learning framework that integrates reinforcement learning, model predictive control, and particle swarm optimization to improve UAV trajectory planning and dynamic resource management. Song et al. [14] proposed an evolutionary multi-objective reinforcement learning algorithm to jointly optimize UAV trajectories and task offloading, balancing task latency, energy consumption, and data collection performance. Furthermore, Zhou et al. [15] extended learning-based frameworks to support real-time radio map construction, caching, and online task offloading, significantly reducing service latency under UAV energy constraints.

Despite these efforts, several limitations persist. Most existing methods either overlook the coupling between UAV trajectories and computation offloading in dynamic channels, or fail to consider multiple timescales in decision-making [16,17]. Additionally, achieving low-latency, energy-efficient, and stable UAV-MEC operations under time-varying channels remains an open problem, particularly in large-scale, multi-UAV scenarios with high-dimensional state and action spaces. These challenges motivate the need for an adaptive framework that can jointly optimize UAV trajectory, task offloading, and resource allocation while capturing channel dynamics and ensuring real-time adaptability.

To address these challenges, this paper proposes an Adaptive UAV Edge Intelligence Framework (AUEIF). The key contributions are summarized as follows:

• We develop a dynamic system model that characterizes the spatio-temporal correlations among UAV mobility, task arrivals, and time-varying wireless channel conditions using a graph-based representation.
• We design a hierarchical reinforcement learning architecture in which a high-level actor–critic module plans coarse UAV trajectories, while a low-level deep Q-network performs fine-grained task offloading and resource allocation in real time.
• We introduce an adaptive channel prediction module based on LSTM to anticipate channel state evolution and enhance decision-making efficiency with respect to latency and energy consumption.
• We conduct extensive simulation studies showing that the proposed AUEIF framework outperforms conventional DRL-based and heuristic approaches in terms of latency, energy efficiency, and policy stability under dynamic channel environments.

The remainder of this paper is organized as follows. Section 2 reviews the related work on UAV-assisted mobile edge computing. Section 3 presents the system model and problem formulation. Section 4 details the proposed Adaptive UAV Edge Intelligence Framework (AUEIF) and the hierarchical reinforcement learning algorithm. Section 5 describes the experimental setup. Section 6 presents the simulation results and performance analysis. Finally, Section 7 concludes the paper and discusses potential future research directions.

2. Related Work

Research on UAV-assisted mobile edge computing (MEC) can be categorized into three main directions: (i) joint task offloading and UAV trajectory optimization, (ii) security, anti-jamming, and multi-vehicle or multi-platoon collaboration, and (iii) reinforcement learning-based resource management and UAV-MEC integrated frameworks. The following subsections provide a comprehensive overview.

Many studies have focused on enhancing the performance of mobile edge computing (MEC) systems through the joint optimization of task offloading, communication resources, and UAV trajectories. For instance, Yang et al. [6] investigated a UAV-assisted MEC system with energy harvesting devices, where dynamic task offloading and UAV trajectory control were jointly optimized to minimize the overall energy consumption. Zhang et al. [18] proposed a comprehensive energy-efficient optimization framework for IoT devices, considering three computation modes, namely local execution, direct offloading to UAVs, and UAV-assisted relaying to access points. Their approach jointly optimized task bit allocation, time-slot scheduling, transmit power, and UAV trajectory using Lagrange dual decomposition and successive convex approximation techniques to obtain near-optimal solutions.

In multi-antenna UAV scenarios, Liu et al. [19] studied MISO UAV-assisted MEC networks, jointly optimizing UAV beamforming vectors, CPU frequencies, UAV trajectories, and UE transmit powers to minimize system energy consumption while satisfying task and trajectory constraints. Hui et al. [20] investigated service coverage optimization for UAV-assisted MEC networks, jointly optimizing UAV altitude and task offloading probability to maximize the successful edge computing probability (SECP). Sun et al. [21] proposed a multi-UAV joint optimization framework (JTORATC), which minimizes task completion latency, reduces UAV energy consumption, and maximizes offloaded tasks using decomposition methods for MINLP problems.

Security and robustness in UAV-assisted MEC have been investigated from multiple perspectives. Kwon et al. [22] introduced a self-certified broadcast authentication protocol for intelligent transportation systems (ITS) within UAV-MEC environments, enabling secure communication without relying on centralized authorities while preserving user privacy. Xu et al. [23] developed a joint resource and trajectory optimization framework to maximize secure computation in dual-UAV MEC systems, where one UAV executes computational tasks and a secondary UAV functions as a jammer to suppress potential eavesdroppers. Shao et al. [24] proposed a multi-agent deep reinforcement learning-based resource management scheme to counteract jamming attacks, dynamically adjusting UAV CPU frequency, bandwidth allocation, and channel access to enhance interference resilience.

Energy efficiency and cooperative strategies in multi-platoon or multi-UAV MEC networks have also been extensively studied. Duan et al. [25] formulated a weighted energy-efficiency maximization approach for multi-platoon UAV-assisted MEC systems, leveraging a 2D path tracking model and sequential quadratic programming for trajectory optimization. Zhao et al. [26] presented a cooperative secure transmission and computation (CSTC) strategy to mitigate threats from mobile collusive eavesdroppers, jointly optimizing UAV trajectories, interference beam patterns, transmit power, and task offloading to enhance system-wide security and efficiency.

Recent works leverage deep reinforcement learning and multi-agent frameworks for adaptive UAV-MEC resource management. Apostolopoulos et al. [27] introduced a risk-aware data offloading framework for UAV-assisted MEC under resource uncertainty, modeling user task offloading as a non-cooperative game. Liu et al. [28] developed a joint communication and computation scheduling approach for platooning vehicles using UAV-assisted MEC, incorporating wireless power transfer, air-to-ground and ground-to-air channels, and vehicular computation. Wang et al. [29] proposed a bi-objective ant colony optimization framework (bi-ACO) for UAV trajectory planning and task offloading. Sun et al. [30] developed a two-timescale approach (TJCCT) combining task offloading, computation resource allocation, and UAV trajectory control. Miao et al. [31] presented a drone swarm path planning method for MEC in industrial IoT, integrating global and local UAV path planning with task offloading. Li et al. [32] designed a multi-UAV framework for VR rendering, using a multi-agent deep reinforcement learning algorithm (MATD3) to jointly optimize UAV flight trajectories and rendering task allocation. Chen et al. [33] introduced a game-theory-based task offloading and resource pricing scheme for autonomous UAV-assisted MEC. Peng et al. [34] proposed a multi-UAV sensing-communication-computation integrated framework, using attention-based multi-agent PPO (MAPPO) to minimize weighted energy consumption while satisfying communication and sensing constraints.

Despite extensive research, key challenges remain. Most prior work either separates UAV trajectory planning from task offloading or ignores time-varying air-to-ground channels. Multi-UAV and multi-task coordination under dynamic environments is challenging due to high-dimensional state-action spaces and real-time decision requirements. Moreover, integrating latency, energy efficiency, reliability, and security in a unified framework remains underexplored. These limitations motivate the design of an adaptive hierarchical UAV edge intelligence framework that jointly optimizes UAV trajectories, computation offloading, and resource allocation under time-varying channels, which is the focus of this paper.

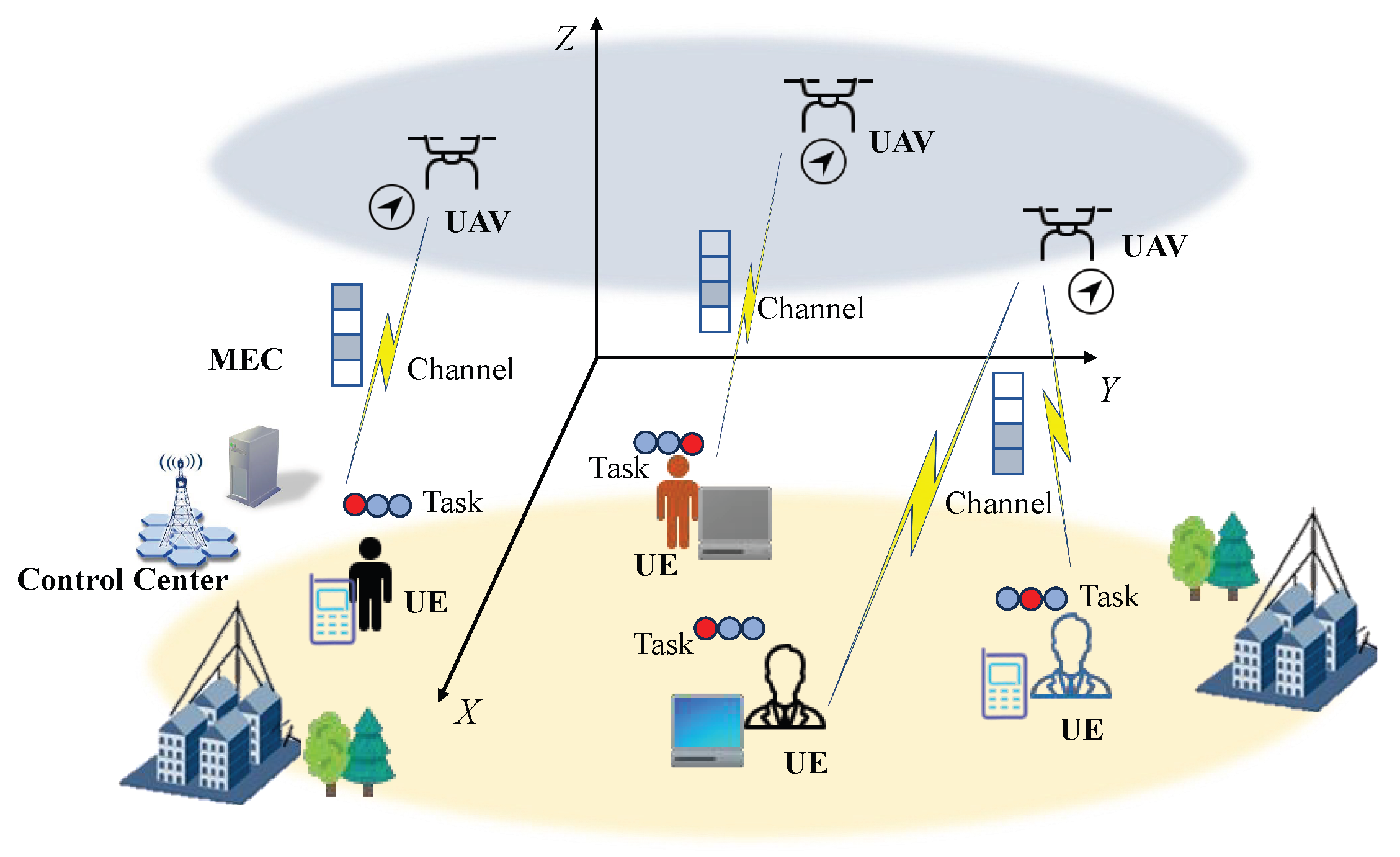
3. System Model

As depicted in Figure 1, we consider a multi-UAV-assisted mobile edge computing (MEC) network consisting of U UAVs and M user equipment (UE) over a total task period T. The time horizon is discretized into N equal-duration slots, each of length $\delta t=T/N$. The UAVs collaborate to serve UEs by jointly optimizing task offloading ratios, UAV computation resource allocation, three-dimensional trajectories, and adaptive weight scheduling to handle heterogeneous workloads and dynamic task arrivals. The primary goal is to minimize a weighted combination of system latency and energy consumption while ensuring UAV flight safety, communication, and computation constraints are satisfied. The main symbols in the system are shown in

Table 1. Key notations in multi-UAV MEC system.

Symbol	Description	Symbol	Description
U	Number of UAVs	M	Number of UEs
T	Total task period (s)	N	Number of time slots
$\delta t$	Duration of each slot (s)	${\mathbf{q}}_u\left(n\right)$	UAV u 3D position at slot n
$H_u\left(n\right)$	UAV altitude (m)	$x_u\left(n\right),y_u\left(n\right)$	UAV horizontal coordinates (m)
${\mathbf{o}}_k$	Obstacle k center (m)	$R_k$	Obstacle radius (m)
$L_{\mathrm{safe}}$	Min distance to obstacle (m)	$L_{\mathrm{col}}$	Min inter-UAV distance (m)
${\mathbf{v}}_u\left(n\right)$	UAV velocity (m/s)	$v_{\max }$	Max UAV speed (m/s)
${\theta }_u\left(n\right)$	UAV heading angle (rad)	${\theta }_{\max }$	Max heading angle (rad)
$\delta t_{\mathrm{fly}}$	Flying duration (s)	$\delta t_{\mathrm{hov}}$	Hovering duration (s)
${\mathcal{M}}_u\left(n\right)$	UEs served by UAV u	${\eta }_{m,u}\left(n\right)$	Offloading fraction of UE m
$D_m\left(n\right)$	Task data size (bits)	$R_{u,m}\left(n\right)$	Transmission rate (bits/s)
$E_u\left(n\right)$	UAV energy (J)	$E_{\mathrm{fly}}\left(n\right)$	Flying energy (J)
$E_{\mathrm{hov}}\left(n\right)$	Hovering energy (J)	$M_u$	UAV mass (kg)
$p_{\mathrm{hov}}$	Hovering power (W)	${\mathbf{w}}_m\left(n\right)$	UE position (m)
$h_{u,m}\left(n\right)$	Channel gain	${\beta }_0$	Reference channel gain
$\alpha$	Path loss exponent	$g_{u,m}\left(n\right)$	Small-scale fading
$B_{m,n}$	Bandwidth (Hz)	$p_m\left(n\right)$	UE transmit power (W)
${\sigma }^2$	Noise power (W)	$K_n$	Number of subchannels
${\mathcal{U}}_m\left(n\right)$	UAVs serving UE m	$f_m^{\mathrm{UE}}$	UE CPU frequency
$C_m$	CPU cycles per bit	$k_m$	UE computation energy coefficient
$f_{m,u}^{\mathrm{UAV}}\left(n\right)$	UAV computation allocation	$k_u$	UAV energy coefficient
$f_u^{\mathrm{UAV}}$	Total UAV CPU capacity	$T_m^{\mathrm{loc}}\left(n\right)$	UE local computation latency
$T_{m,u}^{\mathrm{off}}\left(n\right)$	Offloaded latency	$E_m^{\mathrm{loc}}\left(n\right)$	UE local computation energy
$E_{m,u}^{\mathrm{off}}\left(n\right)$	Offloading energy	$T_{\mathrm{total}}$	Total system latency
$E_{\mathrm{total}}$	Total system energy	$\varphi$	Weight for UAV energy
F	Weighted objective	${\omega }_T,{\omega }_E$	Latency/energy weights
${\omega }_0$	Initial latency weight	${\eta }_{\mathrm{sys}}$	System workload utilization
$E_{\mathrm{rem}}\left(n\right)$	Remaining UAV energy	$E_u^{\max }$	Max UAV energy capacity

.

3.1. UAV Three-Dimensional Trajectory and Collision Avoidance

Let ${\mathbf{q}}_u\left(n\right)={[x_u\left(n\right),y_u\left(n\right),H_u\left(n\right)]}^T$ denote the three-dimensional (3D) position of UAV u at time slot n, where $x_u\left(n\right)$ and $y_u\left(n\right)$ are the horizontal coordinates and $H_u\left(n\right)$ is the altitude. Formally,

$${\mathbf{q}}_u\left(n\right)={[x_u\left(n\right),y_u\left(n\right),H_u\left(n\right)]}^T,\hspace{1em}u=1,2,\dots ,U,$$

(1)

where $x_u\left(n\right),y_u\left(n\right)$ are in meters (m) and $H_u\left(n\right)$ satisfies the altitude limits $H\min \le H_u\left(n\right)\le H\max$.

To avoid inter-UAV collisions, a minimum separation distance $L_{\mathrm{col}}$ is enforced between UAV pairs:

$$\parallel {\mathbf{q}}_u\left(n\right)-{\mathbf{q}}_{u^{\prime }}\left(n\right)\parallel \ge L_{\mathrm{col}},\hspace{1em}\forall u\ne u^{\prime }.$$

(2)

Static obstacles are modeled as spheres with centers ${\mathbf{o}}_k={[x_k,y_k,H_k]}^T$ and radius $R_k$. UAVs must maintain a minimum safe distance $L_{\mathrm{safe}}$ from obstacles:

$$\parallel {\mathbf{q}}_u\left(n\right)-{\mathbf{o}}_k\parallel \ge R_k+L_{\mathrm{safe}},\hspace{1em}\forall k,$$

(3)

where $\parallel ·\parallel$ denotes the Euclidean norm.

To avoid inter-UAV collisions, a minimum separation distance $L_{\mathrm{col}}$ is enforced between UAV pairs:

$$|\mathbf{q}u\left(n\right)-\mathbf{q}{u}^{\prime }\left(n\right)|\ge L_{\mathrm{col}},\hspace{1em}\forall u\ne u^{\prime }.$$

(4)

UAV velocities are constrained by both speed and heading angle:

$${\mathbf{v}}_u\left(n\right)={\displaystyle \frac{{\mathbf{q}}_u(n+1)-{\mathbf{q}}_u\left(n\right)}{\delta t}},\hspace{1em}0\le \parallel {\mathbf{v}}_u\left(n\right)\parallel \le v_{\max },\hspace{1em}\left|{\theta }_u\left(n\right)\right|\le {\theta }_{\max },$$

(5)

where $\mathbf{v}u\left(n\right)$ is the velocity vector of UAV u, $v\max$ is the maximum UAV speed, and ${\theta }_u\left(n\right)$ is the heading angle relative to the x-axis.

Each time slot $\delta t$ is divided into flying and hovering durations:

$$\delta t=\delta t_{\mathrm{fly}}+\delta t_{\mathrm{hov}},\hspace{1em}\delta t_{\mathrm{hov}}=\underset{m\in \mathcal{M}u\left(n\right)}{\max }{\displaystyle \frac{\eta m,u\left(n\right)D_m\left(n\right)}{R_{u,m}\left(n\right)}},$$

(6)

where $\delta t_{\mathrm{fly}}$ and $\delta t_{\mathrm{hov}}$ are the flight and hovering times, respectively. Here, $\mathcal{M}u\left(n\right)$ is the set of UEs served by UAV u, $\eta m,u\left(n\right)$ is the fraction of UE m’s task offloaded to UAV u, $D_m\left(n\right)$ is the task data size (in bits), and $R_{u,m}\left(n\right)$ is the uplink transmission rate (in bits/s).

The energy consumption of UAV u in slot n is composed of flying and hovering components:

$$\begin{array}{cc}\hfill E_u\left(n\right)& =E_{\mathrm{fly}}\left(n\right)+E_{\mathrm{hov}}\left(n\right),\hfill \\ \hfill E_{\mathrm{fly}}\left(n\right)& ={\displaystyle \frac{1}{2}}{M}_u{\parallel {\mathbf{v}}_u\left(n\right)\parallel }^2,\hfill \\ \hfill E_{\mathrm{hov}}\left(n\right)& =p_{\mathrm{hov}}\delta t_{\mathrm{hov}},\hfill \end{array}$$

(7)

where $M_u$ is the UAV mass (kg), $p_{\mathrm{hov}}$ is hovering power (W), $E_{\mathrm{fly}}\left(n\right)$ represents the kinetic energy associated with UAV motion, and $E_{\mathrm{hov}}\left(n\right)$ is the energy consumed while hovering.

3.2. UAV–UE Communication Model

The air-to-ground channel gain between UAV u and UE m is modeled as

$$h_{u,m}\left(n\right)={\beta }_0{d}_{u,m}{\left(n\right)}^{-\alpha }{g}_{u,m}\left(n\right),\hspace{1em}{d}_{u,m}\left(n\right)=|{\mathbf{q}}_u\left(n\right)-\mathbf{w}m\left(n\right)|,$$

(8)

where ${\beta }_0$ is the reference path gain at 1 m, $\alpha$ is the path loss exponent, $g_{u,m}\left(n\right)$ represents small-scale fading, and ${\mathbf{w}}_m\left(n\right)$ is the UE’s position.

The achievable uplink rate is given by Shannon’s formula:

$$R_{u,m}\left(n\right)=B_{m,n}{log}_2\left(1+{\displaystyle \frac{p_m\left(n\right){\left|h_{u,m}\left(n\right)\right|}^2}{{\sigma }^2}}\right),\hspace{1em}{B}_{m,n}={\displaystyle \frac{W}{K_n}},$$

(9)

where $B_{m,n}$ is the bandwidth allocated to UE m, $p_m\left(n\right)$ is the UE transmit power, ${\sigma }^2$ is noise power, W is total system bandwidth, and $K_n$ is the number of subchannels.

For multi-UAV cooperation, the total rate received by UE m is

$$R^{\mathrm{tot}}m\left(n\right)=\sum u\in \mathcal{U}m\left(n\right)Ru,m\left(n\right),$$

(10)

where ${\mathcal{U}}_m\left(n\right)$ is the set of UAVs serving UE m.

3.3. Computation Offloading Model

The local computation latency at UE m is

$$T^{\mathrm{loc}}m\left(n\right)={\displaystyle \frac{C_m{D}_m\left(n\right)\left(1-{\sum }_u\eta m,u\left(n\right)\right)}{f_m^{\mathrm{UE}}}},$$

(11)

where $C_m$ is the required CPU cycles per bit, and $f_m^{\mathrm{UE}}$ is the UE CPU frequency. The corresponding energy consumption is

$$E_m^{\mathrm{loc}}\left(n\right)=k_m{\left(f_m^{\mathrm{UE}}\right)}^3{T}_m^{\mathrm{loc}}\left(n\right),$$

(12)

with $k_m$ being the UE computation energy coefficient.

For offloaded tasks, the UAV computation latency is:

$$T^{\mathrm{off}}m,u\left(n\right)={\displaystyle \frac{\eta m,u\left(n\right)D_m\left(n\right)}{R_{u,m}\left(n\right)}}+{\displaystyle \frac{{\eta }_{m,u}\left(n\right)D_m\left(n\right)C_m}{f^{\mathrm{UAV}}m,u\left(n\right)}},$$

(13)

and the energy consumption for offloading is:

$$E^{\mathrm{off}}m,u\left(n\right)=p_m\left(n\right){\displaystyle \frac{{\eta }_{m,u}\left(n\right)D_m\left(n\right)}{R_{u,m}\left(n\right)}}+k_u{\left(f^{\mathrm{UAV}}m,u\left(n\right)\right)}^2\eta m,u\left(n\right)D_m\left(n\right)C_m,$$

(14)

where $f_{m,u}^{\mathrm{UAV}}\left(n\right)$ is the computation resource allocated to UE m by UAV u, and $k_u$ is the UAV computation energy coefficient.

Constraints on UAV computation resources and offloading fractions are

$$\sum _{m\in \mathcal{M}u\left(n\right)}{f}^{\mathrm{UAV}}m,u\left(n\right)\le f_u^{\mathrm{UAV}},\hspace{1em}0\le {\eta }_{m,u}\left(n\right)\le 1,\hspace{1em}\sum _{u\in \mathcal{U}m\left(n\right)}\eta m,u\left(n\right)\le 1.$$

(15)

3.4. Weighted System Objective Function

The total latency and energy consumption of the system are

$$T_{\mathrm{total}}=\sum _{n=1}^N\sum _{m=1}^M\max \left(T^{\mathrm{loc}}m\left(n\right),\sum u\in \mathcal{U}m\left(n\right)T^{\mathrm{off}}m,u\left(n\right)\right),$$

(16)

$$E_{\mathrm{total}}=\sum _{n=1}^N\sum _{m=1}^M{E}^{\mathrm{loc}}m\left(n\right)+\varphi \sum {u=1}^U\sum _{n=1}^N{E}_u\left(n\right)+\sum _{n=1}^N\sum _{m=1}^M\sum _{u\in \mathcal{U}m\left(n\right)}{E}^{\mathrm{off}}m,u\left(n\right),$$

(17)

where $\varphi$ is a weighting factor to balance UAV energy in the system-level objective.

The weighted sum objective is

$$F={\omega }_T\widehat{T}\mathrm{total}+{\omega }_E\widehat{E}\mathrm{total},\hspace{1em}{\omega }_T+{\omega }_E=1,$$

(18)

where $\widehat{T}\mathrm{total}$ and $\widehat{E}\mathrm{total}$ are normalized latency and energy metrics, and the dynamic weights are adapted as

$${\omega }_T\left(n\right)={\omega }_0+\alpha {\eta }_{\mathrm{sys}}-\beta {\displaystyle \frac{E_{\mathrm{rem}}\left(n\right)}{{\sum }_{u=1}^U{E}_u^{\max }}},\hspace{1em}{\omega }_E\left(n\right)=1-{\omega }_T\left(n\right),$$

(19)

with ${\omega }_0$ being the initial latency weight, ${\eta }_{\mathrm{sys}}$ representing the system-level workload utilization, $E_{\mathrm{rem}}\left(n\right)$ the remaining energy of all UAVs, and $E_u^{\max }$ the maximum UAV energy capacity. The parameters $\alpha$ and $\beta$ are design coefficients that control the sensitivity of the objective weights to system workload utilization and remaining energy, respectively. Specifically, $\alpha$ regulates the emphasis on latency minimization under high workload conditions, while $\beta$ determines the extent to which energy conservation is prioritized as the overall UAV energy budget decreases.

3.5. Problem Formulation

The joint optimization problem aims to minimize the weighted sum of total system latency and total energy consumption across all UAVs and UEs, by jointly optimizing UAV trajectories, UE offloading ratios, transmit powers, and UAV computation resource allocations. Let ${\mathbf{q}}_u\left[n\right]$ denote the 3D position of UAV u at time slot n, ${\eta }_{m,u}\left[n\right]$ the task offloading fraction from UE m to UAV u, $p_m\left[n\right]$ the UE transmit power, and $f_{m,u}^{\mathrm{UAV}}\left[n\right]$ the computation resource allocated by UAV u to UE m. The optimization problem is formulated as

$$\begin{array}{cc}\mathcal{P}:\hfill & \underset{\begin{array}{c}{\mathbf{q}}_u\left[n\right],\hspace{1em}{\eta }_{m,u}\left[n\right],\\ p_m\left[n\right],\hspace{1em}{f}_{m,u}^{\mathrm{UAV}}\left[n\right]\end{array}}{\min }F\hfill \\ & \mathrm{s}.\mathrm{t}.\mathrm{C}1:0\le {\eta }_{m,u}\left[n\right]\le 1,\hspace{1em}\forall m\in \mathcal{M}, u\in {\mathcal{U}}_m\left[n\right], n\in \mathcal{N},\hfill \\ & \mathrm{C}2:\sum _{u\in {\mathcal{U}}_m\left[n\right]}{\eta }_{m,u}\left[n\right]\le 1,\hspace{1em}\forall m\in \mathcal{M}, n\in \mathcal{N},\hfill \\ & \mathrm{C}3:{\mathbf{q}}_u\left[1\right]={\mathbf{q}}_u[N+1],\hspace{1em}\forall u\in \mathcal{U},\hfill \\ & \mathrm{C}4: \parallel {\mathbf{q}}_u[n+1]-{\mathbf{q}}_u\left[n\right]\parallel \le v_{\max }\delta t,\hspace{1em}\forall u\in \mathcal{U}, n\in \mathcal{N},\hfill \\ & \mathrm{C}5: \parallel {\mathbf{q}}_u\left[n\right]-{\mathbf{q}}_{u^{\prime }}\left[n\right]\parallel \le L_{\mathrm{col}},\hspace{1em}\forall u\ne u^{\prime }, n\in \mathcal{N},\hfill \\ & \mathrm{C}6: \parallel {\mathbf{q}}_u\left[n\right]-{\mathbf{o}}_k\parallel \ge R_k+L_{\mathrm{safe}},\hspace{1em}\forall k,u\in \mathcal{U}, n\in \mathcal{N},\hfill \\ & \mathrm{C}7:H_{\min }\le H_u\left[n\right]\le H_{\max },\hspace{1em}\forall u\in \mathcal{U}, n\in \mathcal{N},\hfill \\ & \mathrm{C}8:0\le p_m\left[n\right]\le P_{m,\max },\hspace{1em}\forall m\in \mathcal{M}, n\in \mathcal{N},\hfill \\ & \mathrm{C}9:\sum _{m\in {\mathcal{M}}_u\left[n\right]}{f}_{m,u}^{\mathrm{UAV}}\left[n\right]\le f_u^{\mathrm{UAV}},\hspace{1em}\forall u\in \mathcal{U}, n\in \mathcal{N},\hfill \\ & \mathrm{C}10:\sum _{n\in \mathcal{N}}{f}_{m,u}^{\mathrm{UAV}}\left[n\right]\delta t\ge C_m\sum _{n\in \mathcal{N}}{\eta }_{m,u}\left[n\right]D_m\left(n\right),\hspace{1em}\forall m\in \mathcal{M}, u\in {\mathcal{U}}_m\left[n\right],\hfill \\ & \mathrm{C}11:E_m^{\mathrm{loc}}\left(n\right)+\sum _{u\in {\mathcal{U}}_m\left[n\right]}{E}_{m,u}^{\mathrm{off}}\left(n\right)\le E_{m,\max },\hspace{1em}\forall m\in \mathcal{M}, n\in \mathcal{N}.\hfill \end{array}$$

(20)

Constraints C1–C2 ensure that the offloading ratios are valid and do not exceed the total task size. Constraints C3–C7 enforce UAV trajectory continuity, collision avoidance, obstacle clearance, and altitude limits. Constraint C8 restricts UE transmit power. Constraints C9–C10 enforce UAV computation resource limits and guarantee task processing completion. Constraint C11 ensures that UE energy budgets are not exceeded.

4. Approach Design

To address the coupled optimization of UAV trajectory planning and computation offloading under highly dynamic air-to-ground channels, we propose an Adaptive UAV Edge Intelligence Framework (AUEIF). This framework is designed to simultaneously capture the spatial and temporal correlations among UAV mobility, wireless channel fluctuations, and computational workload distributions, enabling adaptive, reliable, and efficient decision-making in complex aerial networks.

AUEIF comprises three principal components. First, a dynamic graph-based modeling approach is employed to represent the UAV-MEC network topology and its time-varying channel states, facilitating explicit reasoning over the spatial relationships among UAVs, ground users, and communication links. Second, an LSTM-based channel prediction module is incorporated to forecast short-term channel variations, mitigating uncertainty and enhancing the accuracy and reliability of trajectory and offloading decisions. Third, a hierarchical reinforcement learning (HRL) strategy is utilized for real-time joint optimization, where macro-level policies determine UAV mobility and navigation, while micro-level policies optimize task offloading ratios, computational resource allocation, and transmission power, thereby achieving coordinated and efficient UAV-MEC operation.

4.1. Dynamic Graph Construction

To accurately capture the spatio-temporal dynamics of the UAV-MEC network, we represent the system as a dynamic graph $\mathcal{G}\left[n\right]$ at each discrete time slot n:

$$\mathcal{G}\left[n\right]=\left(\mathcal{V}\right[n],\mathcal{E}[n\left]\right),$$

(21)

where $\mathcal{V}\left[n\right]$ denotes the set of nodes and $\mathcal{E}\left[n\right]$ represents the set of edges encoding communication links between nodes. The node set is defined as

$$\mathcal{V}\left[n\right]=\{{\mathbf{q}}_u\left[n\right],{\mathbf{w}}_m\left[n\right]\},\hspace{1em}u\in \mathcal{U}, m\in \mathcal{M},$$

(22)

where ${\mathbf{q}}_u\left[n\right]$ corresponds to the three-dimensional position of UAV u at time slot n, and ${\mathbf{w}}_m\left[n\right]$ captures the state of user equipment (UE) m, encompassing its location and computational workload. By integrating both UAV spatial positions and UE computational attributes into the graph nodes, this formulation provides a unified representation of network mobility and task demand, serving as a rigorous basis for coordinated trajectory planning and adaptive offloading strategies.

Edges are used to represent the time-varying communication quality between UAVs and UEs:

$$\mathcal{E}\left[n\right]=\left\{h_{u,m}\left[n\right]\right\},\hspace{1em}{h}_{u,m}\left[n\right]={\beta }_0{d}_{u,m}^{-\alpha }\left[n\right]g_{u,m}\left[n\right],$$

(23)

where $d_{u,m}\left[n\right]$ is the Euclidean distance between UAV u and UE m, ${\beta }_0$ is the reference channel gain in free-space conditions, $\alpha$ is the path-loss exponent, and $g_{u,m}\left[n\right]$ accounts for small-scale fading effects. This formulation captures both the deterministic path-loss attenuation and the stochastic variations induced by the wireless environment, thus providing a realistic representation of the air-to-ground channel for subsequent decision-making.

To support graph-based reasoning and learning, we construct an adjacency matrix:

$$\mathbf{A}\left[n\right]=\left[a_{u,m}\left[n\right]\right],\hspace{1em}{a}_{u,m}\left[n\right]=f\left(h_{u,m}\left[n\right]\right),$$

(24)

where $f(·)$ normalizes the raw channel gains to edge weights that reflect link quality. By emphasizing stronger links and attenuating weaker ones, this adjacency matrix not only facilitates effective message propagation in graph-based models but also informs UAV trajectory and offloading decisions with an explicit awareness of the current network topology and channel conditions.

4.2. LSTM-Based Channel Prediction

While the dynamic graph captures the instantaneous spatial structure and communication topology, UAV trajectory planning and task offloading decisions are also strongly affected by temporal channel variations. To model these dynamics, we adopt a long short-term memory (LSTM) network to forecast future channel states:

$${\widehat{h}}_{u,m}[n+\Delta ]=\mathrm{LSTM}\left(h_{u,m}[n-\tau :n]\right),$$

(25)

where $\tau$ denotes the historical observation window and $\Delta$ is the prediction horizon. By leveraging temporal correlations in the observed channel sequences, the LSTM enables the system to anticipate future channel conditions, which is critical for robust and proactive trajectory and offloading optimization.

The LSTM updates its internal memory through gated mechanisms:

$$\mathbf{c}\left[n\right]=\mathbf{f}\left[n\right]\odot \mathbf{c}[n-1]+\mathbf{i}\left[n\right]\odot \tilde{\mathbf{c}}\left[n\right],$$

(26)

where $\mathbf{f}\left[n\right]$ and $\mathbf{i}\left[n\right]$ are the forget and input gates, respectively, $\tilde{\mathbf{c}}\left[n\right]$ is the candidate cell state, and ⊙ denotes element-wise multiplication. This structure ensures that relevant historical information is preserved while outdated or less informative data is filtered out, improving the accuracy of channel prediction.

The predicted channel states are subsequently integrated into the UAV decision-making framework:

$${\eta }_{m,u}\left[n\right]=\mathrm{softmax}\left(f_{\theta }({\widehat{h}}_{u,m}[n+\Delta ],D_m\left[n\right],E_{\mathrm{rem},u}\left[n\right])\right),$$

(27)

where $D_m\left[n\right]$ is the task size and $E_{\mathrm{rem},u}\left[n\right]$ represents the remaining energy of UAV u. By fusing the structural insights from the dynamic graph with the temporally predicted channel states, the framework enables anticipatory and adaptive control, allowing UAVs to proactively adjust trajectories and offloading strategies to mitigate the impact of sudden channel fluctuations.

4.3. Hierarchical Reinforcement Learning Framework

By combining dynamic graph information with LSTM-predicted channels, we obtain a rich spatio-temporal representation, which enables the agent to make proactive decisions rather than purely reactive ones.

Based on this spatio-temporal input, the joint UAV trajectory and computation offloading problem is formulated as a Markov Decision Process (MDP) $(\mathcal{S},\mathcal{A},P,R,\gamma )$. The system state at time slot n is defined as

$$\mathbf{s}\left[n\right]=\{{\mathbf{q}}_u\left[n\right],{\mathbf{v}}_u\left[n\right],{\widehat{h}}_{u,m}\left[n\right],E_{\mathrm{rem},u}\left[n\right],D_m\left[n\right],{\eta }_{m,u}[n-1],f_{m,u}^{\mathrm{UAV}}[n-1],p_m[n-1]\},$$

(28)

where ${\widehat{h}}_{u,m}\left[n\right]$ incorporates the LSTM-predicted channel gains. This state captures UAV positions, velocities, energy levels, task requirements, and prior resource allocation decisions, integrating both spatial and temporal information. Correspondingly, the action vector is defined as

$$\mathbf{a}\left[n\right]=\{\Delta {\mathbf{q}}_u\left[n\right],{\eta }_{m,u}\left[n\right],f_{m,u}^{\mathrm{UAV}}\left[n\right],p_m\left[n\right]\},$$

(29)

where the macro-scale component $\Delta {\mathbf{q}}_u\left[n\right]$ governs UAV trajectory adjustments, while micro-scale actions ${\eta }_{m,u}\left[n\right],f_{m,u}^{\mathrm{UAV}}\left[n\right],p_m\left[n\right]$ control task offloading, computation resource allocation, and transmit power.

The reward function is designed to balance latency and energy consumption:

$$r\left[n\right]=-\sum _m\left({\widehat{T}}_m\left[n\right]+{\lambda }_E{\widehat{E}}_m\left[n\right]\right),$$

(30)

where ${\widehat{T}}_m\left[n\right]$ and ${\widehat{E}}_m\left[n\right]$ denote latency and energy consumption for UE m, and ${\lambda }_E$ is a weighting factor adjusting the trade-off between energy efficiency and latency reduction. By maximizing cumulative rewards, the agent implicitly seeks to optimize both trajectory planning and offloading decisions over the mission horizon.

To address the hierarchical structure of decision-making, we adopt a two-level reinforcement learning (RL) architecture. At the high level, the HL actor–critic agent observes aggregated state information, including UAV positions, velocities, predicted channel states, and residual energy:

$${\mathbf{s}}^{\mathrm{HL}}\left[n\right]=\{{\mathbf{q}}_u\left[n\right],{\mathbf{v}}_u\left[n\right],{\widehat{h}}_{u,m}\left[n\right],E_{\mathrm{rem},u}\left[n\right]\},$$

(31)

and generates coarse trajectory adjustments ${\mathbf{a}}^{\mathrm{HL}}\left[n\right]=\Delta {\mathbf{q}}_u\left[n\right]$. The HL agent is designed to capture long-term strategic behaviors by accumulating low-level rewards over a macro horizon $K_H$, and updates its policy using an actor–critic formulation:

$$\begin{array}{cc}\hfill V^{\mathrm{HL}}\left({\mathbf{s}}^{\mathrm{HL}}\left[n\right]\right)& =\mathbb{E}\left[\sum _{k=0}^{\infty }{\gamma }^k{r}^{\mathrm{HL}}[n+k]| {\mathbf{s}}^{\mathrm{HL}}\left[n\right]\right],\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill {\theta }^{\mathrm{HL}}& \leftarrow {\theta }^{\mathrm{HL}}+{\alpha }_{\mathrm{HL}}{\nabla }_{{\theta }^{\mathrm{HL}}}\mathbb{E}\left[A^{\mathrm{HL}}({\mathbf{s}}^{\mathrm{HL}}\left[n\right],{\mathbf{a}}^{\mathrm{HL}}\left[n\right])\right],\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill A^{\mathrm{HL}}(\mathbf{s},\mathbf{a})& =Q^{\mathrm{HL}}(\mathbf{s},\mathbf{a})-V^{\mathrm{HL}}\left(\mathbf{s}\right),\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill r^{\mathrm{HL}}\left[n\right]& =\sum _{k=0}^{K_H}{\gamma }^k{r}^{\mathrm{LL}}[n+k].\hfill \end{array}$$

(35)

This hierarchical design enables the HL agent to effectively capture global trajectory strategies and long-term objectives, while coordinating with the low-level agent for fine-grained control over task offloading, resource allocation, and UAV mobility.

At the low level, the LL agent operates at a finer temporal resolution, observing detailed system states including UAV positions, predicted channel states, task sizes, and prior resource allocations:

$${\mathbf{s}}^{\mathrm{LL}}\left[n\right]=\{{\mathbf{q}}_u\left[n\right],{\widehat{h}}_{u,m}\left[n\right],D_m\left[n\right],{\eta }_{m,u}[n-1],f_{m,u}^{\mathrm{UAV}}[n-1],p_m[n-1]\},$$

(36)

and produces micro-scale actions:

$${\mathbf{a}}^{\mathrm{LL}}\left[n\right]=\{{\eta }_{m,u}\left[n\right],f_{m,u}^{\mathrm{UAV}}\left[n\right],p_m\left[n\right]\}.$$

(37)

The LL agent is trained via Double Deep Q-Network (DDQN) to ensure stable and robust learning, updating its Q-function as follows:

$$\begin{array}{cc}\hfill Q({\mathbf{s}}^{\mathrm{LL}}\left[n\right],{\mathbf{a}}^{\mathrm{LL}}\left[n\right];\varphi )& =\mathbb{E}\left[\sum _{t=n}^N{\gamma }^{t-n}{r}^{\mathrm{LL}}\left[t\right]|{\mathbf{s}}^{\mathrm{LL}}\left[n\right],{\mathbf{a}}^{\mathrm{LL}}\left[n\right]\right],\hfill \\ \hfill \varphi & \leftarrow \varphi -{\alpha }_{\mathrm{LL}}{\nabla }_{\varphi }(r^{\mathrm{LL}}\left[n\right]+\gamma \underset{{\mathbf{a}}^{\prime }}{\max }Q({\mathbf{s}}^{\mathrm{LL}}[n+1],{\mathbf{a}}^{\prime };{\varphi }^{-})\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill & -Q({\mathbf{s}}^{\mathrm{LL}}\left[n\right],{\mathbf{a}}^{\mathrm{LL}}\left[n\right];\varphi ){)}^2.\hfill \end{array}$$

(39)

The hierarchical framework operates through iterative interaction with a simulated environment that captures dynamic UAV network behaviors, including task arrivals, UAV mobility, and time-varying air-to-ground channels. At each time slot n, the high-level agent first observes the coarse state ${\mathbf{s}}^{\mathrm{HL}}\left[n\right]$ and outputs a trajectory adjustment $\Delta {\mathbf{q}}_u\left[n\right]$, which defines a feasible spatial region constraining the low-level action space and ensuring safety and energy feasibility. Subsequently, the low-level agent observes the fine-grained state ${\mathbf{s}}^{\mathrm{LL}}\left[n\right]$, encompassing UAV positions, predicted channel gains ${\widehat{h}}_{u,m}\left[n\right]$, pending task sizes $D_m\left[n\right]$, and previous allocation decisions ${\eta }_{m,u}[n-1]$, $f_{m,u}^{\mathrm{UAV}}[n-1]$, $p_m[n-1]$. Utilizing the learned Q-function $Q({\mathbf{s}}^{\mathrm{LL}}\left[n\right],{\mathbf{a}}^{\mathrm{LL}}\left[n\right];\varphi )$, the LL agent determines the optimal micro-actions:

$${\mathbf{a}}^{\mathrm{LL}\ast }\left[n\right]=\arg \underset{{\mathbf{a}}^{\mathrm{LL}}}{\max }Q({\mathbf{s}}^{\mathrm{LL}}\left[n\right],{\mathbf{a}}^{\mathrm{LL}};\varphi ),$$

(40)

which jointly specify the task offloading ratio ${\eta }_{m,u}\left[n\right]$, the allocated UAV computation resources $f_{m,u}^{\mathrm{UAV}}\left[n\right]$, and the transmission power $p_m\left[n\right]$. These actions drive the environment to transition to the next state $\mathbf{s}[n+1]$, yielding an immediate low-level reward $r^{\mathrm{LL}}\left[n\right]$. Aggregating these rewards over the macro horizon $K_H$ provides long-term feedback to update the high-level agent, enabling coordinated trajectory optimization while ensuring responsive micro-level control over computation and communication resources.

To stabilize training, both HL and LL agents maintain experience replay buffers. For the LL DDQN, mini-batches of transitions $({\mathbf{s}}^{\mathrm{LL}}\left[n\right],{\mathbf{a}}^{\mathrm{LL}}\left[n\right],r^{\mathrm{LL}}\left[n\right],{\mathbf{s}}^{\mathrm{LL}}[n+1])$ are sampled to update the parameters $\varphi$ via gradient descent. The HL actor–critic network updates its policy parameters ${\theta }^{\mathrm{HL}}$ using the aggregated rewards $r^{\mathrm{HL}}\left[n\right]$, ensuring that long-term objectives such as energy efficiency and mission completion are considered. During each iteration, the HL policy guides the feasible region of UAV trajectories, and the LL policy selects micro-scale actions within this region, creating a feedback loop where LL performance informs HL policy improvement, and HL guidance constrains LL exploration.

Formally, the training and decision-making process can be summarized as a sequential procedure: at each time slot, the HL agent observes ${\mathbf{s}}^{\mathrm{HL}}\left[n\right]$ and produces $\Delta {\mathbf{q}}_u\left[n\right]$ according to its policy ${\pi }^{\mathrm{HL}}({\mathbf{s}}^{\mathrm{HL}}\left[n\right];{\theta }^{\mathrm{HL}})$, defining the permissible movement for each UAV. Within this feasible region, the LL agent observes ${\mathbf{s}}^{\mathrm{LL}}\left[n\right]$ and computes the optimal action ${\mathbf{a}}^{\mathrm{LL}\ast }\left[n\right]$ that maximizes its Q-function. The joint action $(\Delta {\mathbf{q}}_u\left[n\right],{\mathbf{a}}^{\mathrm{LL}\ast }\left[n\right])$ is then executed, the environment transitions to $\mathbf{s}[n+1]$, and the low-level reward $r^{\mathrm{LL}}\left[n\right]$ is obtained. Both agents update their respective networks using their experience buffers and reward signals, and the process continues iteratively until the cumulative reward converges.

Upon convergence, the learned hierarchical policy generates a sequence of coordinated outputs over the entire mission horizon:

$${\{{\mathbf{q}}_u\left[n\right],{\eta }_{m,u}\left[n\right],f_{m,u}^{\mathrm{UAV}}\left[n\right],p_m\left[n\right]\}}_{n=1}^N,$$

(41)

which represent optimized UAV trajectories, task offloading ratios, computation resource allocations, and transmit powers for each UAV and UE. This framework allows the system to adaptively balance latency and energy consumption while responding to dynamic network topologies and predicted channel variations. By embedding predicted channel states into both HL and LL agents, the hierarchical reinforcement learning approach effectively anticipates future network conditions, enabling proactive and coordinated optimization of UAV trajectory and computation offloading. The pseudo-code implementation is presented in Algorithm 1.

Algorithm 1: Hierarchical UAV Trajectory and Computation Offloading via HRL

The computational complexity of the proposed AUEIF framework mainly stems from hierarchical policy inference, dynamic graph processing, and LSTM-based channel prediction. The high-level (HL) policy operates on a coarse time scale and performs a single forward inference to generate macro-level trajectory adjustments, resulting in constant per-decision complexity. The low-level (LL) DDQN policy executes fine-grained task offloading and resource allocation, with computational complexity scaling linearly with the number of UAV–UE associations, i.e., $\mathcal{O}(U·M)$. The dynamic graph construction and LSTM-based channel prediction introduce only fixed or near-linear overhead due to sparse connectivity and short temporal observation windows. During online deployment, AUEIF relies exclusively on forward inference without iterative optimization, leading to millisecond-level per-slot execution time, which satisfies the real-time requirements of UAV-assisted MEC systems.

5. Experiment Setting

5.1. System Parameters

We consider a multi-UAV-assisted MEC network comprising U UAVs and M UEs, where the numbers of UAVs and UEs vary within the ranges $U\in [2,6]$ and $M\in [5,20]$, respectively. The network operates in a three-dimensional airspace with dimensions of 1000–$1500 \mathrm{m}\times 1000$–$1500 \mathrm{m}\times 400$–$600 \mathrm{m}$. UEs are assumed to follow random mobility patterns with velocities uniformly distributed in the range of 1 to $5 \mathrm{m}/\mathrm{s}$. In each time slot, UEs generate computational tasks with heterogeneous sizes $D_m\left[n\right]\in [5\times {10}^6,2\times {10}^7]$ bits, thereby capturing realistic variations in workload demand.

UAVs have a maximum flight speed $v_{\max }\in [15,25] \mathrm{m}/\mathrm{s}$ and a maximum heading angle ${\theta }_{\max }\in [\pi /6,\pi /3]$ rad, while their physical properties such as mass $M_u$ and hovering power $p_{\mathrm{hov}}$ can vary in the ranges $M_u\in [4,6]$ kg and $p_{\mathrm{hov}}\in [120,180]$ W, respectively. The onboard energy capacity is configurable within $E_{\max }\in [4000,6000]$ J, and the total CPU computing power is set to $f_u^{\mathrm{UAV}}\in [0.8,1.2]\times {10}^9$ cycles per second.

For the communication subsystem, the air-to-ground wireless links are modeled by jointly considering large-scale path loss and small-scale Rayleigh fading. The reference channel gain ${\beta }_0$ is set within the range of $-35$ to $-25$ dBm, with the path loss exponent $\alpha \in [2.5,3.0]$ and the noise power spectral density ${\sigma }^2\in [-180,-170]$ dBm/Hz. The total available system bandwidth is configured as $W\in [15,25]$ MHz and is evenly partitioned into $K\in [8,12]$ orthogonal subchannels. Each UE is subject to a maximum transmit power constraint $P_{m,\max }\in [15,25]$ dBm. To emulate realistic time-varying wireless environments, the small-scale fading coefficients evolve dynamically across time slots with a variation rate in the range of $[0.1,0.3]$. Regarding the computation model, the CPU frequencies of UEs are set within $f_m^{\mathrm{UE}}\in [1.5,2.5]\times {10}^8$ cycles/s, and the required number of CPU cycles per processed bit is $C_m\in [800,1200]$. The energy consumption for computation follows a standard dynamic power model, where the energy coefficients for UEs and UAVs are given by $k_m\in [0.8,1.2]\times {10}^{-28}$ and $k_u\in [4,6]\times {10}^{-29}$ J/(cycle²), respectively.

Flight constraints for the UAVs are specified with minimum and maximum altitudes $H_{\min }\in [40,60]$ m and $H_{\max }\in [140,160]$ m, a minimum inter-UAV separation $L_{\mathrm{col}}\in [40,60]$ m, and a minimum distance to obstacles $L_{\mathrm{safe}}\in [25,35]$ m. Obstacles are modeled as spheres with radii $R_k\in [15,25]$ m, and the number of obstacles can be varied between one and five to study different levels of environmental complexity.

The total task execution horizon T is set within the range of $[80,120]$ s and is discretized into $N\in [40,60]$ equal time slots, resulting in a slot duration of $\delta t=T/N$. The initial system workload utilization factor ${\eta }_{\mathrm{sys}}$ is configured within $[0.3,0.9]$ to reflect different traffic intensities. In the weighted optimization objective, the latency-related weight ${\omega }_0$ is selected from $[0.5,0.7]$, while the corresponding energy weight is defined as ${\omega }_E=1-{\omega }_0$, enabling a balanced trade-off between delay and energy consumption. For channel state prediction, the LSTM-based module leverages a sliding historical observation window of $\tau \in [8,12]$ time slots and produces channel forecasts over a prediction horizon of $\Delta \in [2,5]$ slots, thereby facilitating proactive adaptation to channel dynamics.

5.2. Baseline Methods and Evaluation Metrics

To evaluate the proposed AUEIF framework, we consider the following baselines:

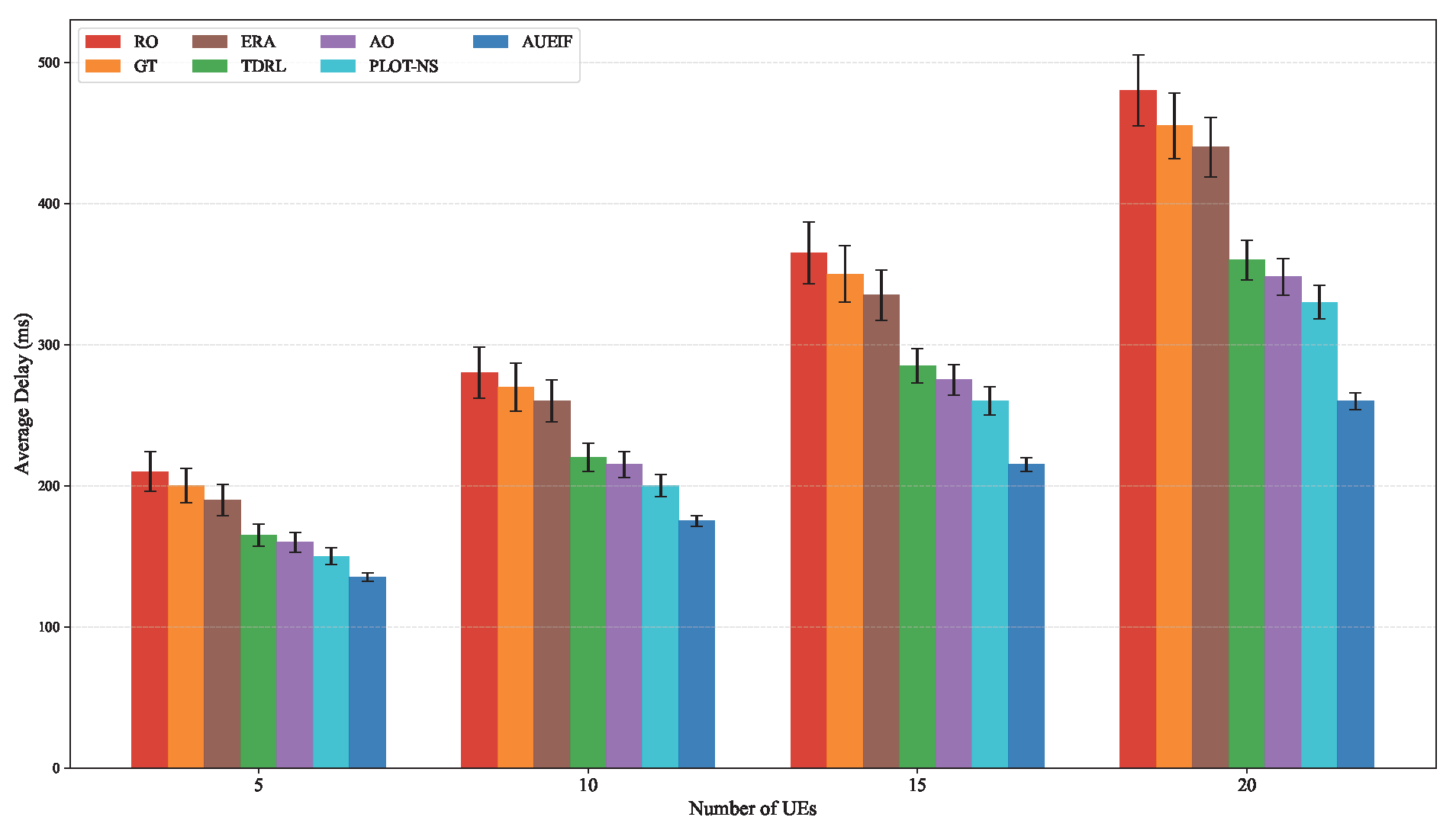
• Random Offloading (RO): UAVs randomly decide task offloading ratios to edge servers and cloud, without trajectory optimization or queue awareness.
• Greedy Trajectory (GT): UAVs always move toward the UE with the largest task queue, without considering channel dynamics or offloading optimization.
• Equal Resource Allocation (ERA): Computation and communication resources are evenly distributed among all UEs and UAVs, without adaptive optimization.
• Time-Driven DRL (TDRL): Deep reinforcement learning algorithm optimizing UAV trajectories, offloading decisions, and transmission power based on time-driven strategy, without task-driven reliability awareness or hybrid action representation.
• Alternating Optimization (AO): Joint optimization of partial offloading, UAV trajectory, user scheduling, edge-cloud computation, and resource allocation using alternating optimization and SCA techniques, without online or task-driven adaptation.
• PLOT without Lyapunov Perturbation (PLOT-NS): Online UAV-MEC algorithm using standard Lyapunov optimization without perturbed control, which may suffer from coupling effects and suboptimal queue stability.

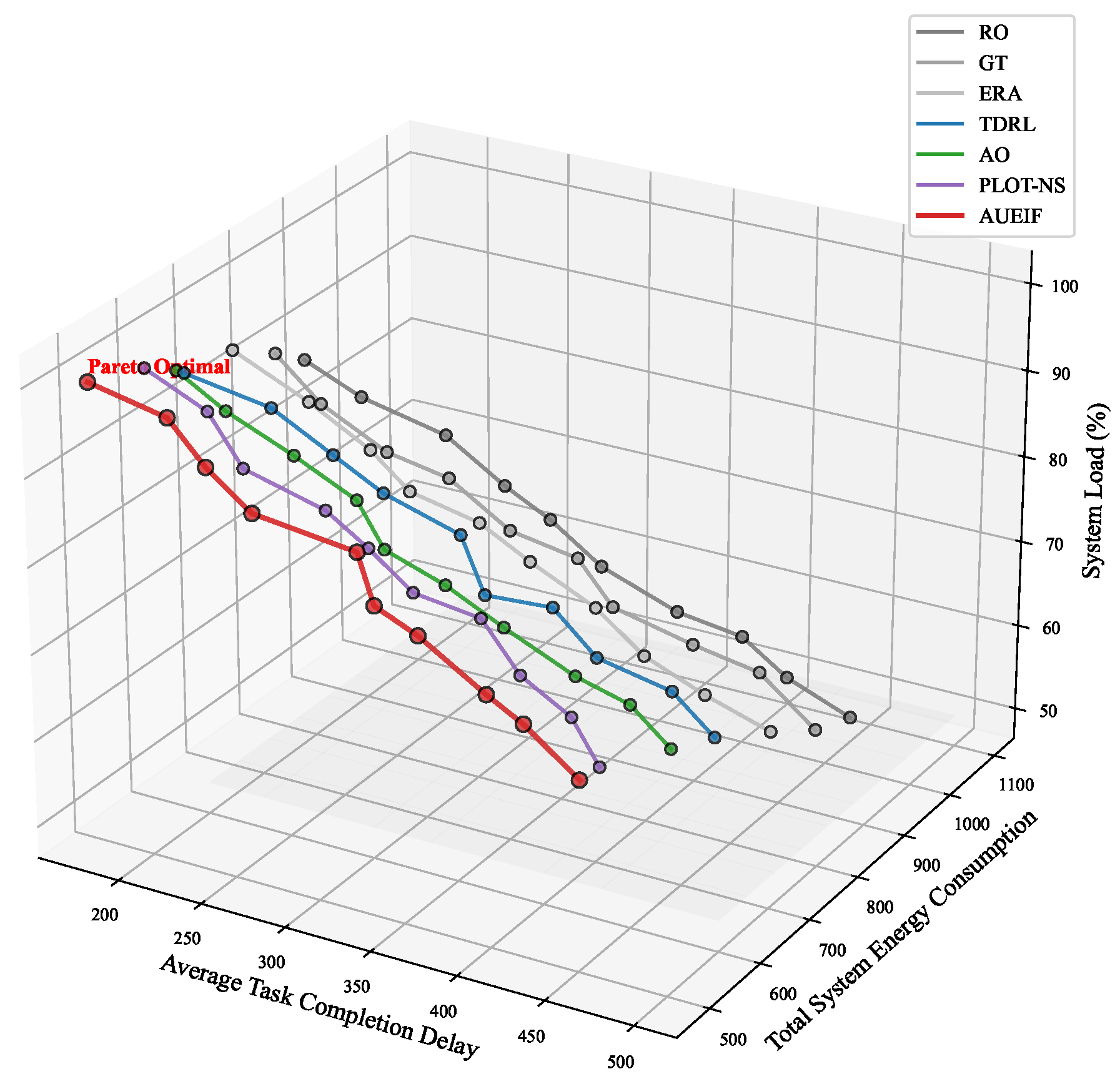
6. Experiment Result

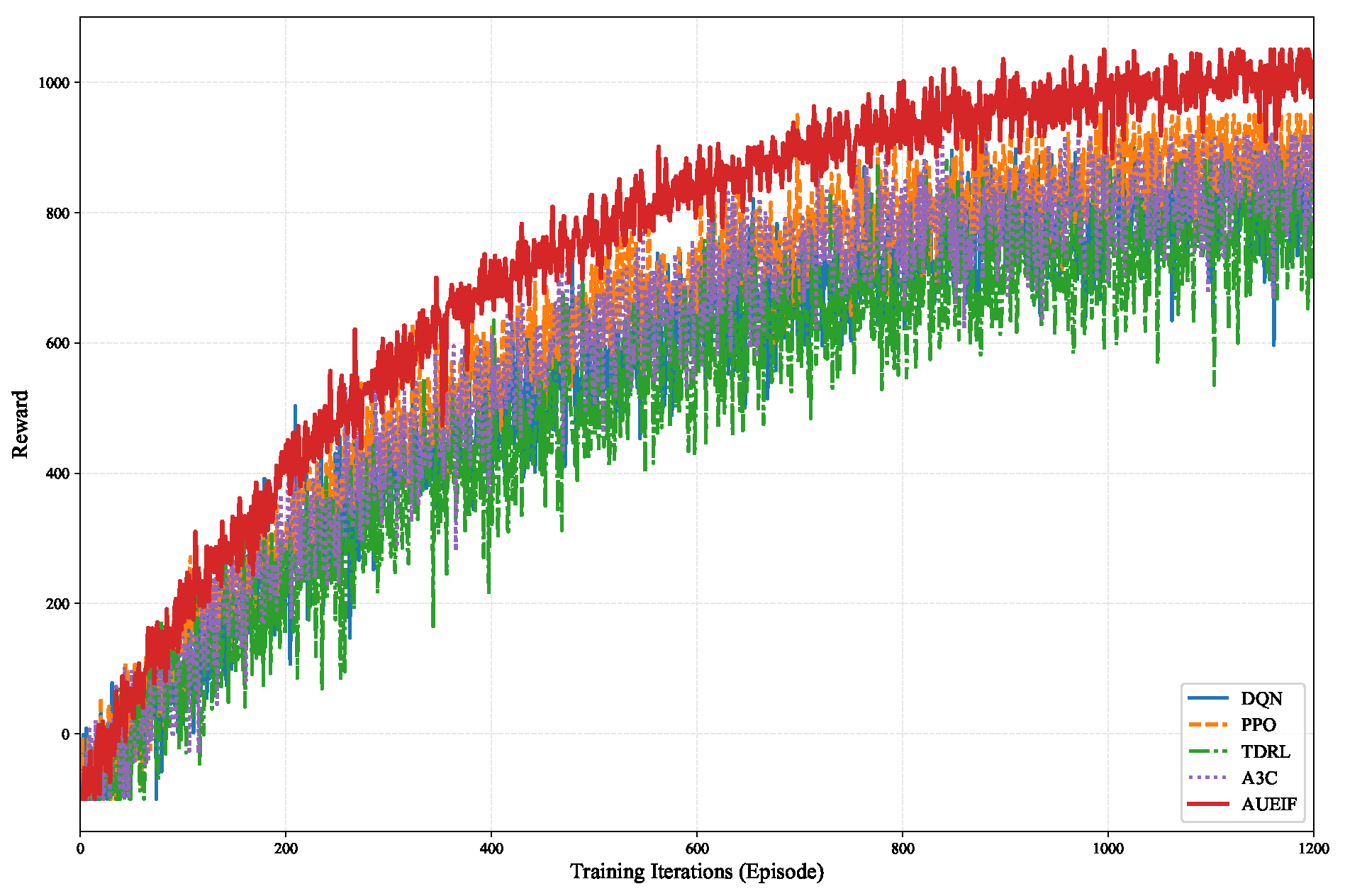
6.1. Convergence Performance Analysis

Figure 2 compares the cumulative reward trajectories of the proposed AUEIF framework with four representative DRL baselines, namely DQN, PPO, TDRL, and A3C. Starting from the initial exploration stage, AUEIF demonstrates consistently faster convergence and higher steady-state rewards than all competing methods. Throughout the training process, AUEIF achieves an average cumulative reward improvement of approximately 15–20% over the strongest baseline. In addition, the reward curve of AUEIF exhibits noticeably reduced variance and smoother convergence behavior, indicating improved training stability in dynamic UAV-assisted MEC environments. These results suggest that the proposed framework more effectively captures the spatio-temporal coupling between UAV mobility and computation offloading decisions, thereby enabling more efficient policy learning and superior long-term performance compared with existing DRL-based approaches.

Figure 3 illustrates the convergence of the AUEIF framework under different learning rates. All curves start from the initial exploration phase, showing that the learning rate significantly affects both convergence speed and stability. Higher learning rates enable faster initial improvement but exhibit larger fluctuations, whereas moderate learning rates achieve a balanced trade-off between convergence speed and smoothness. Lower learning rates converge more gradually and steadily, maintaining stable performance throughout training. Overall, the proposed framework demonstrates substantial performance gains, achieving approximately fifteen to twenty percent higher cumulative reward than the least effective configuration. These results indicate that careful selection of the learning rate is critical for efficient and stable policy learning in dynamic UAV-assisted MEC environments.

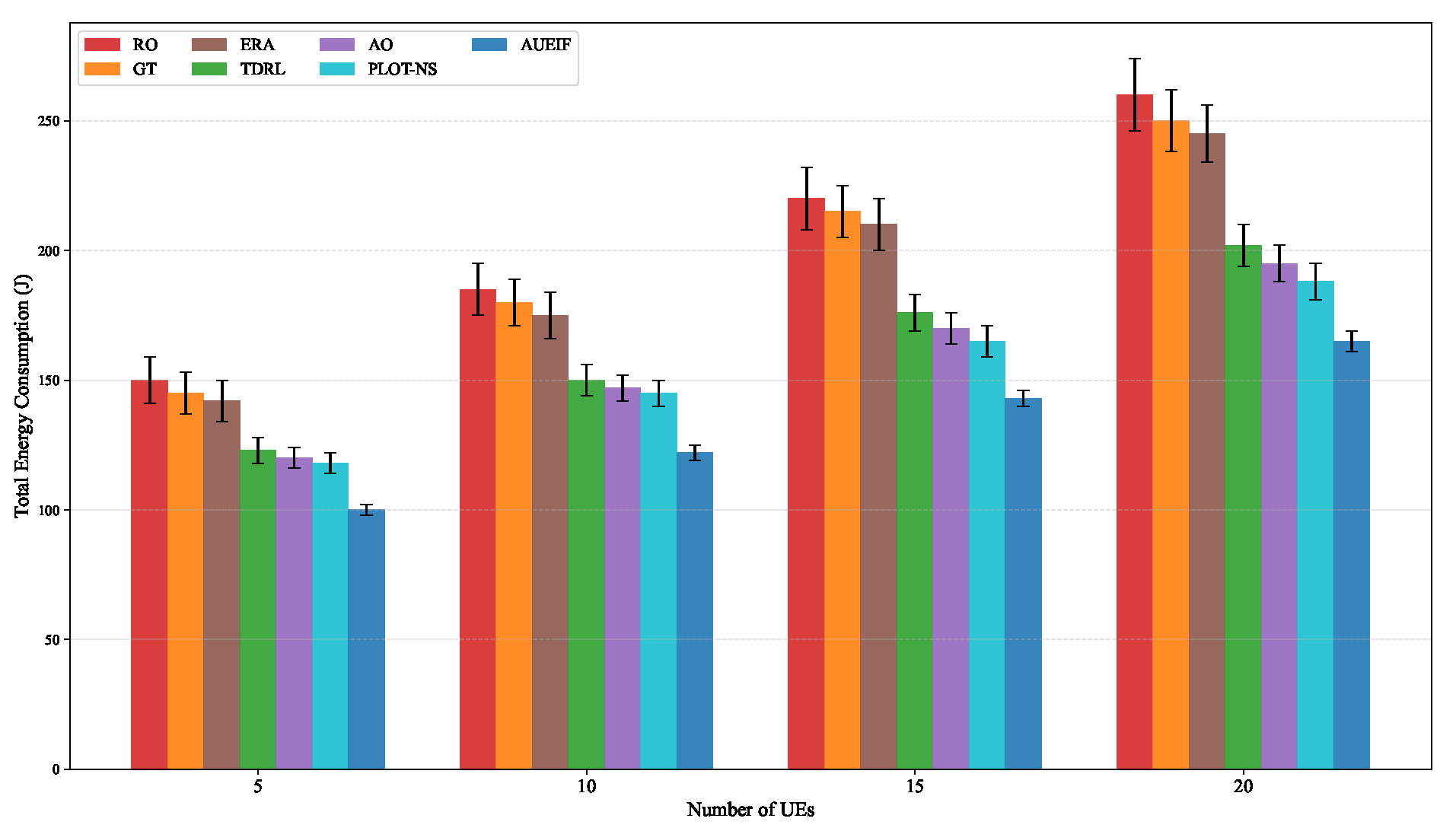
6.2. Differential Performance Analysis Under Varying UE Density

Figure 4 depicts the average task completion delay as the number of UEs increases from light-load to high-density scenarios. As expected, all baseline methods exhibit a monotonic increase in delay due to aggravated channel contention and heightened computational demand. In contrast, AUEIF consistently achieves the lowest delay across the entire range of UE densities. Specifically, compared with heuristic baselines such as RO, GT, and ERA, AUEIF reduces the average delay by more than 40–60%, primarily because these methods lack adaptive trajectory control and coordinated computation allocation mechanisms. Furthermore, even when compared with advanced optimization-based approaches, including TDRL, AO, and PLOT-NS, the AUEIF still attains delay reductions of approximately 20–35%. This performance gain stems from its unified optimization of UAV trajectory planning, task offloading decisions, and resource scheduling. Notably, under heavy-load conditions, the delay curves of baseline methods exhibit sharp growth, whereas AUEIF demonstrates a markedly flatter increase, indicating superior scalability and robustness in high-density UAV-MEC scenarios.

Figure 5 compares the total system energy consumption of AUEIF with that of the benchmark methods. AUEIF consistently exhibits the lowest energy consumption, highlighting its effectiveness in energy-aware operation under dynamic air–ground channel conditions. Heuristic baselines such as RO, GT, and ERA incur more than 50–70% higher energy expenditure due to inefficient UAV trajectories, redundant task processing, and non-adaptive resource allocation. More advanced schemes, including TDRL, AO, and PLOT-NS, achieve partial energy savings; however, they still consume approximately 20–40% more energy than AUEIF, as they do not fully coordinate mobility control, communication, and computation decisions in an online manner. The superior energy efficiency of AUEIF is attributed to the synergistic integration of three mechanisms: energy-aware trajectory optimization that avoids unnecessary UAV maneuvers, task-driven computation offloading that reduces superfluous processing, and adaptive resource allocation that mitigates prolonged high-frequency operation. Overall, AUEIF reduces total energy consumption by over 30% relative to the highest-energy-consuming baselines, demonstrating its ability to achieve energy-efficient UAV-MEC operation without sacrificing task performance.

Figure 6 depicts the three-dimensional Pareto frontier among average task completion delay, total system energy consumption, and system load for all evaluated methods. AUEIF consistently lies on the Pareto-optimal surface, indicating its superior ability to jointly balance latency performance and energy efficiency across different load regimes. In contrast, heuristic baselines such as RO, GT, and ERA are located in dominated regions characterized by simultaneously high delay and excessive energy consumption. Under heavy-load conditions, the AUEIF reduces the average task completion delay by approximately 25% while achieving an energy saving of about 32% relative to these baselines. Even when compared with more advanced schemes, including TDRL, AO, and PLOT-NS, the AUEIF maintains a more favorable trade-off with lower latency and reduced energy usage. These results confirm that the integrated design of trajectory optimization, adaptive computation offloading, and resource allocation in the AUEIF enables more effective multi-objective optimization in UAV-assisted MEC systems.

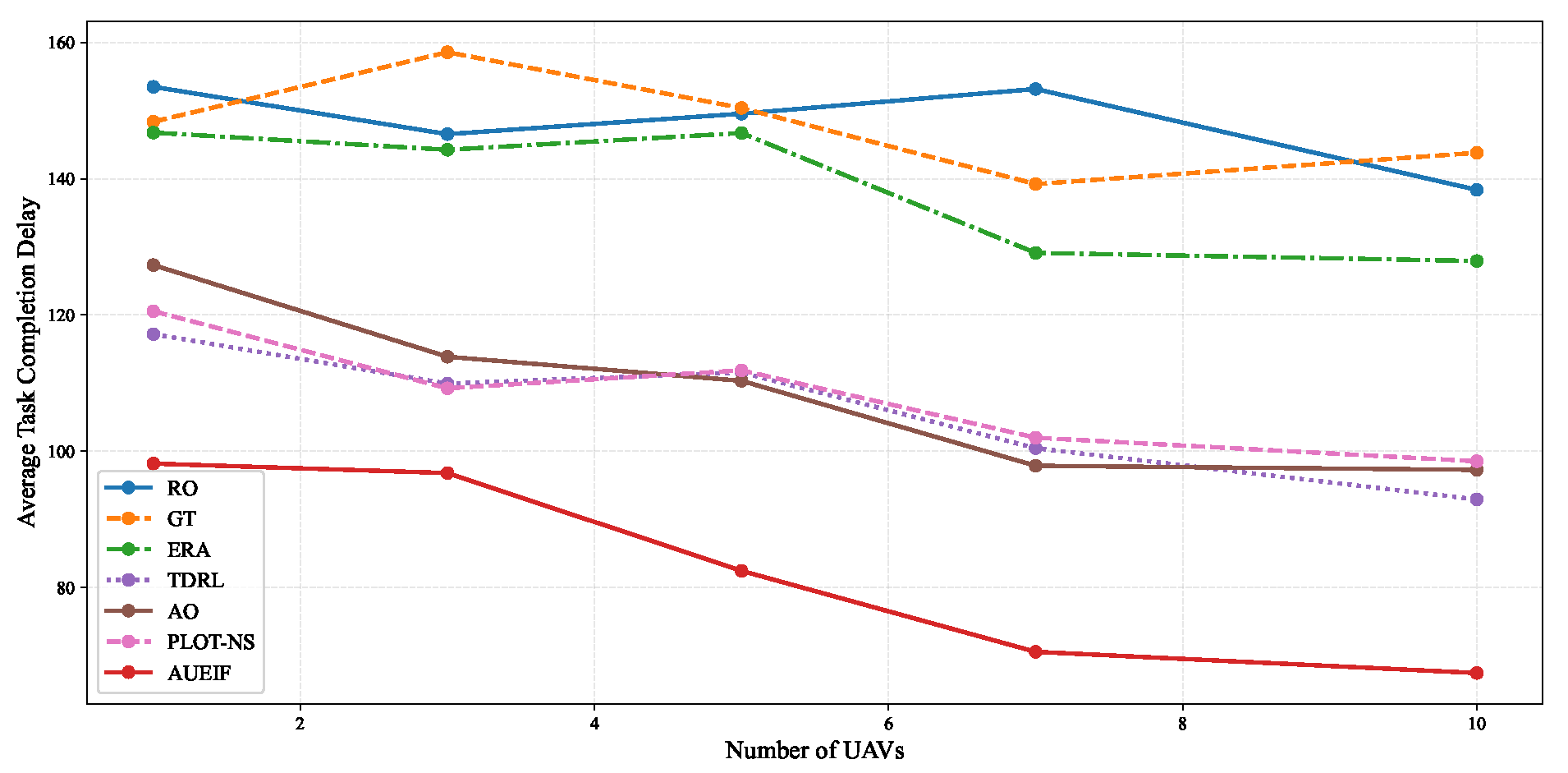
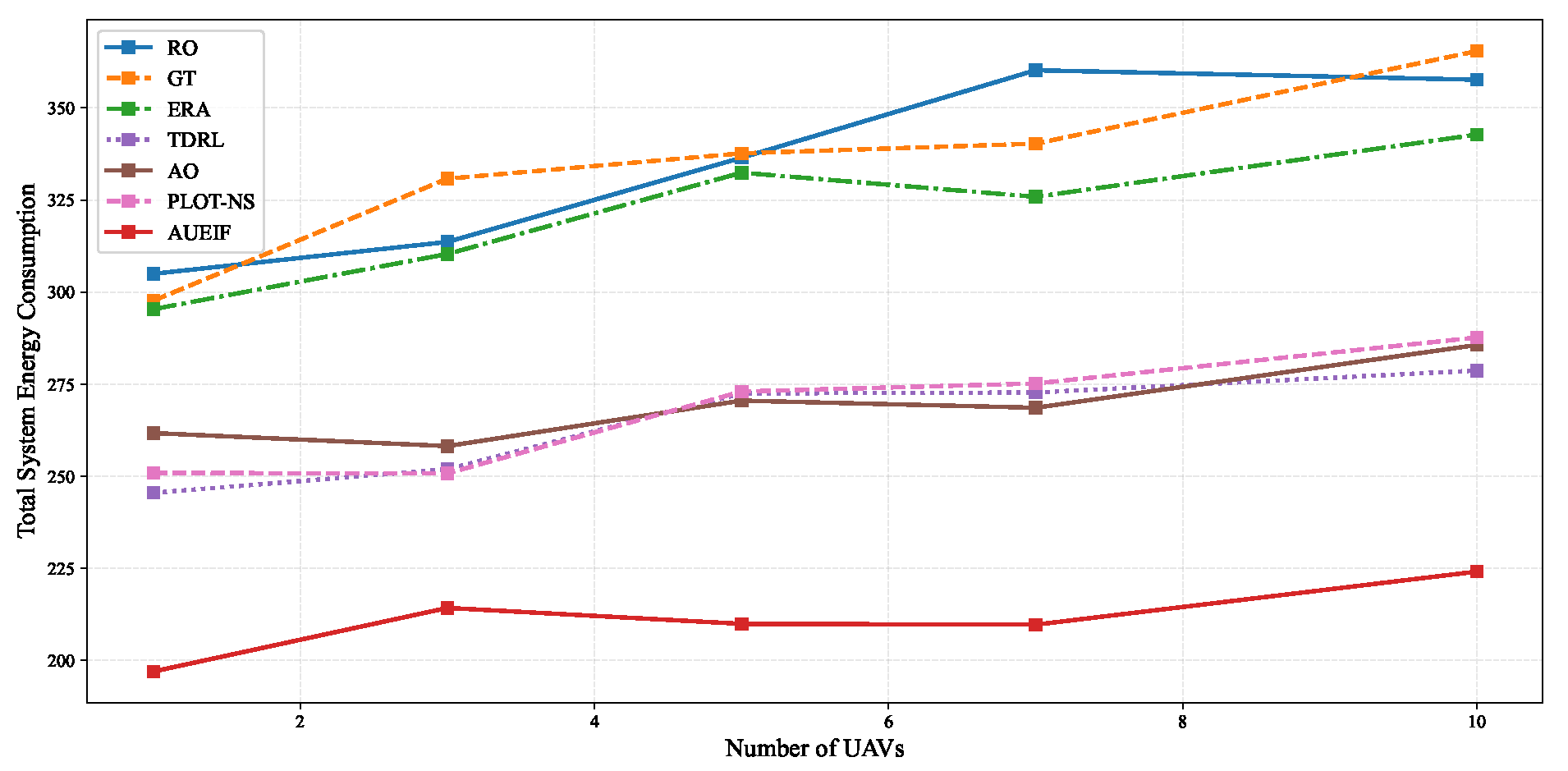
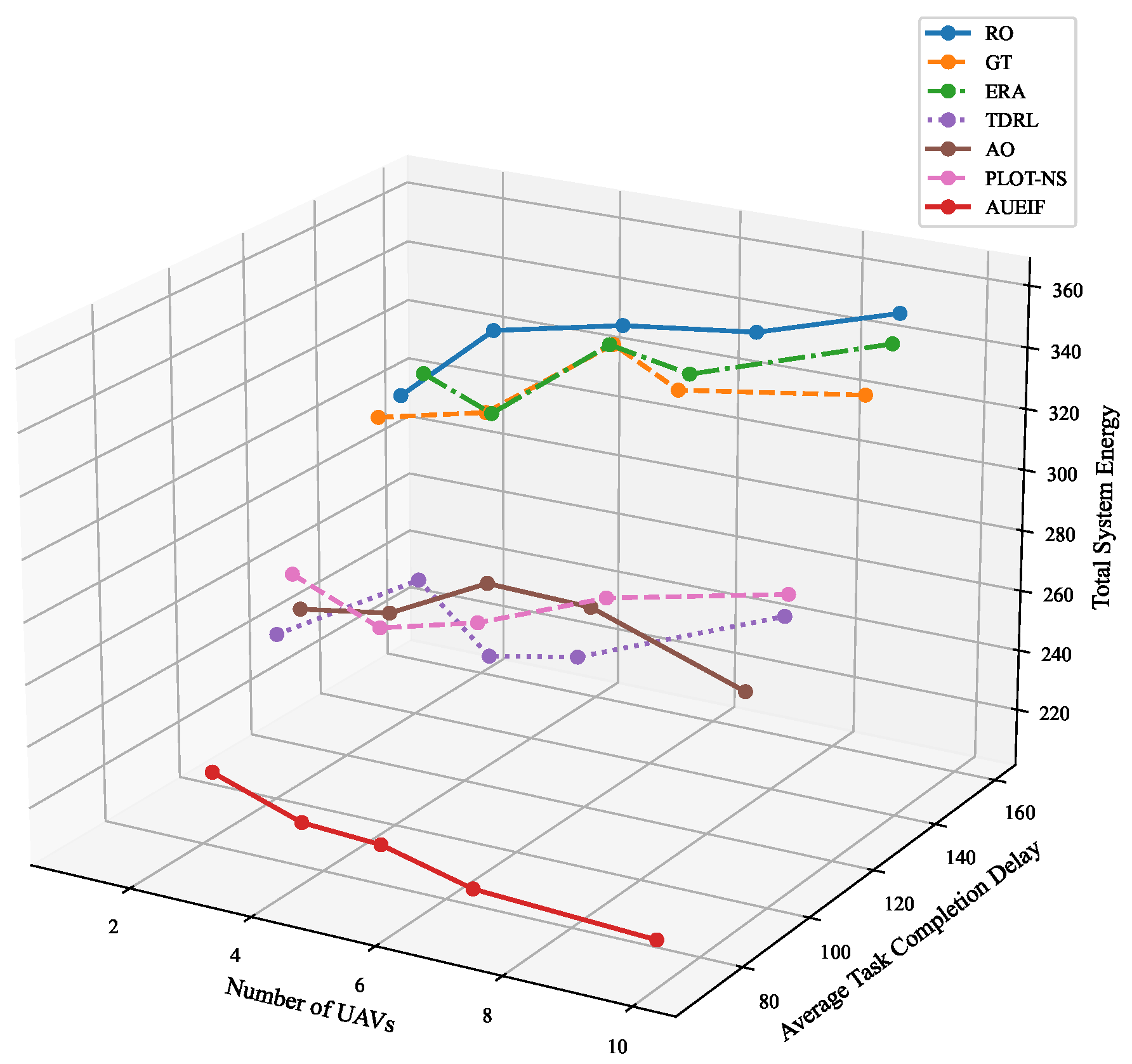
6.3. Differential Performance Analysis Under Varying UAV Density

Figure 7 illustrates the variation in average task completion delay as the number of UAVs increases, where the horizontal axis denotes UAV density and the vertical axis represents the corresponding task completion delay. Each curve corresponds to a different scheme. As the UAV density grows, all methods benefit from the increased availability of computing and communication resources, leading to an overall reduction in delay. However, the AUEIF consistently achieves the lowest task completion delay across all UAV densities. In particular, the AUEIF reduces the average delay by approximately 25–40% compared with advanced baselines and by up to 50–60% relative to heuristic methods. This performance advantage is attributed to the AUEIF’s tightly coupled optimization of UAV trajectory planning, task offloading decisions, and resource allocation, which enables smooth delay reduction and robust adaptation to varying system capacities.

Figure 8 illustrates the variation in total system energy consumption as the number of UAVs increases for different methods. The horizontal axis represents the UAV population, while the vertical axis denotes the total system energy consumption. Each curve corresponds to a specific scheme. As the number of UAVs grows, the overall energy consumption increases for all methods due to higher coordination, communication, and mobility overhead. Nevertheless, the AUEIF consistently achieves the lowest energy consumption across all UAV densities, demonstrating its superior energy efficiency. In contrast, heuristic baselines such as RO, GT, and ERA exhibit the steepest growth in energy usage, consuming approximately 50–70% more energy than the AUEIF under high UAV density. More advanced approaches, including TDRL, AO, and PLOT-NS, provide moderate improvements over the heuristic schemes but still incur about 15–30% higher energy consumption compared with the AUEIF. These results highlight the effectiveness of AUEIF in jointly optimizing UAV trajectories, task-aware computation offloading, and adaptive resource allocation to achieve energy-efficient UAV-MEC operation.

Figure 9 depicts the three-dimensional Pareto frontier among average task completion delay, total system energy consumption, and UAV density for the evaluated methods. The horizontal axis indicates the number of deployed UAVs, the vertical axis represents the average task completion delay, and the depth axis corresponds to the total system energy consumption. Each curve denotes a specific method, with the AUEIF highlighted to emphasize its performance. As UAV density increases, both delay and energy consumption generally exhibit an upward trend, reflecting the additional communication, coordination, and mobility overhead introduced by denser UAV deployments. Notably, the AUEIF consistently occupies the region characterized by lower delay and lower energy consumption in the three-dimensional performance space, indicating a more favorable trade-off between computational efficiency and energy utilization. In contrast, heuristic baselines such as RO, GT, and ERA incur persistently high delay and energy costs across all UAV densities. More advanced schemes, including TDRL, AO, and PLOT-NS, achieve moderate improvements over the heuristic methods but still remain dominated by the AUEIF in terms of both latency and energy efficiency.

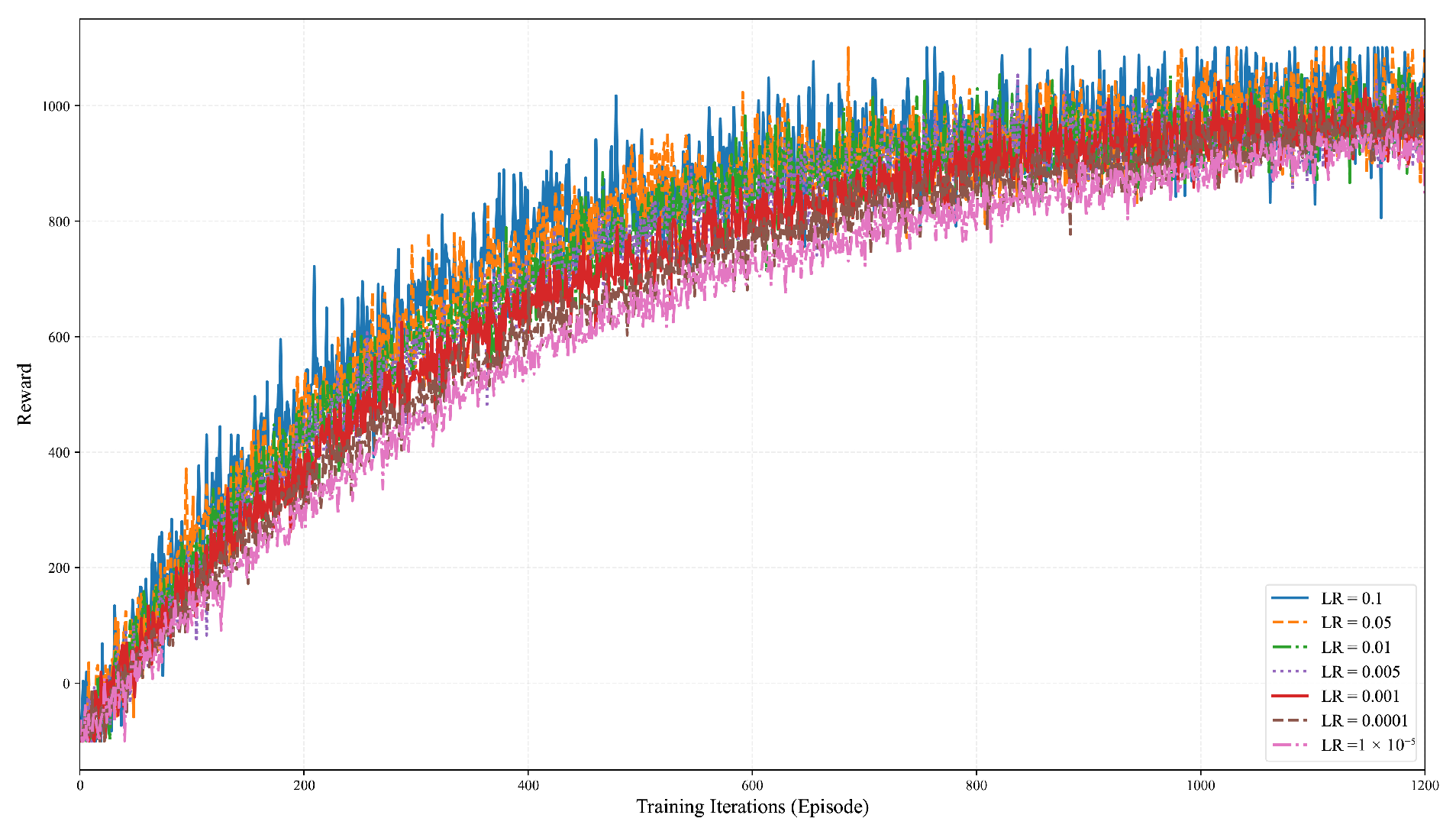
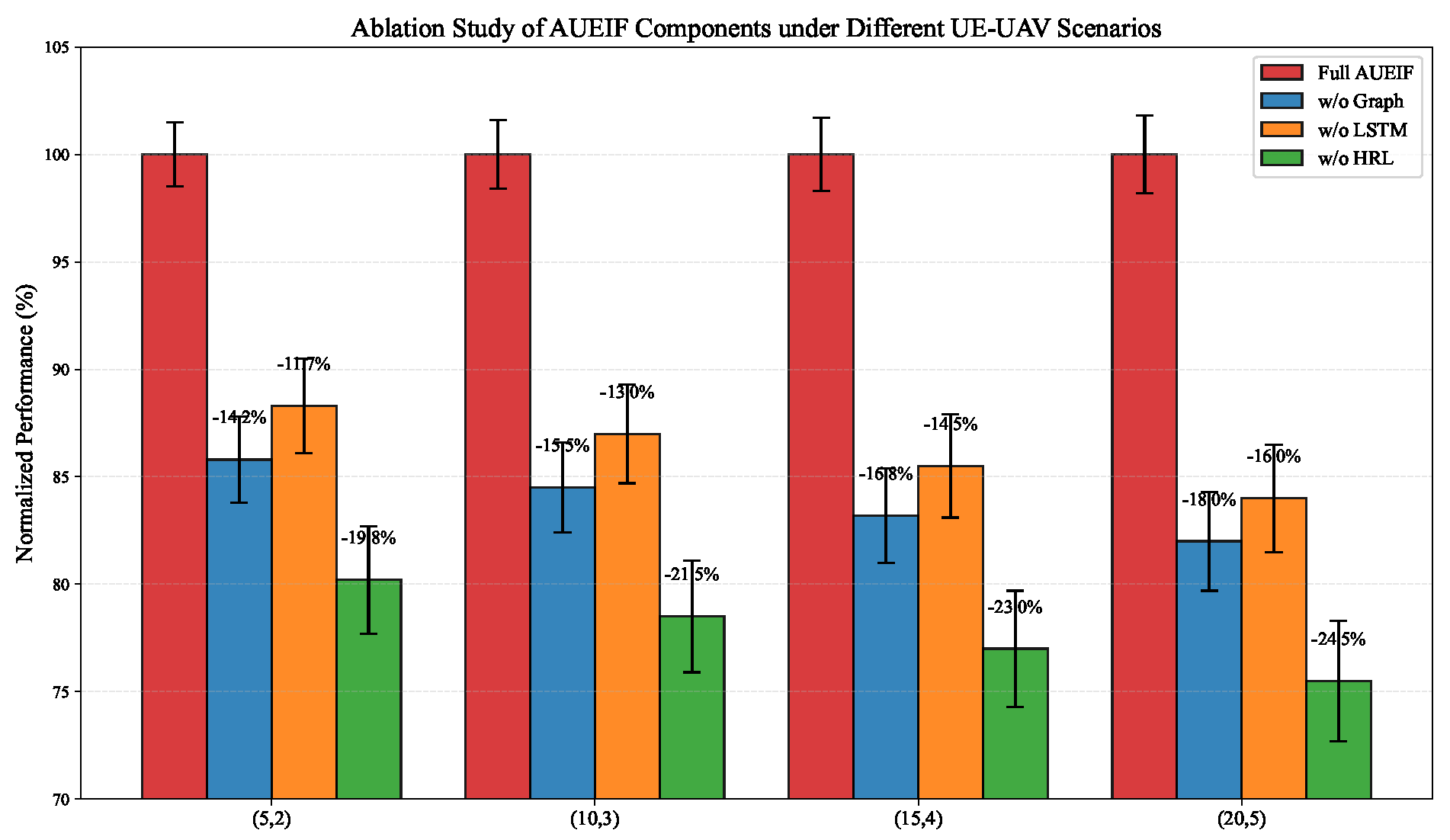
6.4. Ablation Experiment Analysis

Figure 10 presents the ablation study of the AUEIF under varying system scenarios, where the horizontal axis represents different combinations of UE numbers and UAV numbers, reflecting system load and available computing resources. The vertical axis denotes normalized performance in percentage, measured in terms of task success rate or system efficiency, where higher values indicate better performance. Each scenario includes results for four methods: Full AUEIF, representing the complete model with all modules; w/o Graph, which removes the dynamic graph module and thus cannot capture UAV network topology changes; w/o LSTM, which eliminates the LSTM-based channel prediction, reducing the ability to anticipate channel fluctuations; and w/o HRL, which discards the hierarchical reinforcement learning structure, leaving a single-layer policy that must handle the entire high-dimensional joint action space.

The results clearly demonstrate the contribution of each core component. Removing the dynamic graph module leads to a noticeable performance drop, particularly under high-load scenarios, indicating the importance of capturing inter-UAV collaboration. Eliminating the LSTM prediction module further degrades performance, highlighting its role in improving offloading decision accuracy. The most pronounced degradation occurs when the hierarchical reinforcement learning structure is removed, reflecting slower convergence and reduced overall efficiency. Across all scenarios, Full AUEIF consistently outperforms its ablated variants, and the relative performance decline of the ablated models ranges from approximately 15% to 25%, demonstrating that each component significantly contributes to robust and efficient UAV-MEC operations.

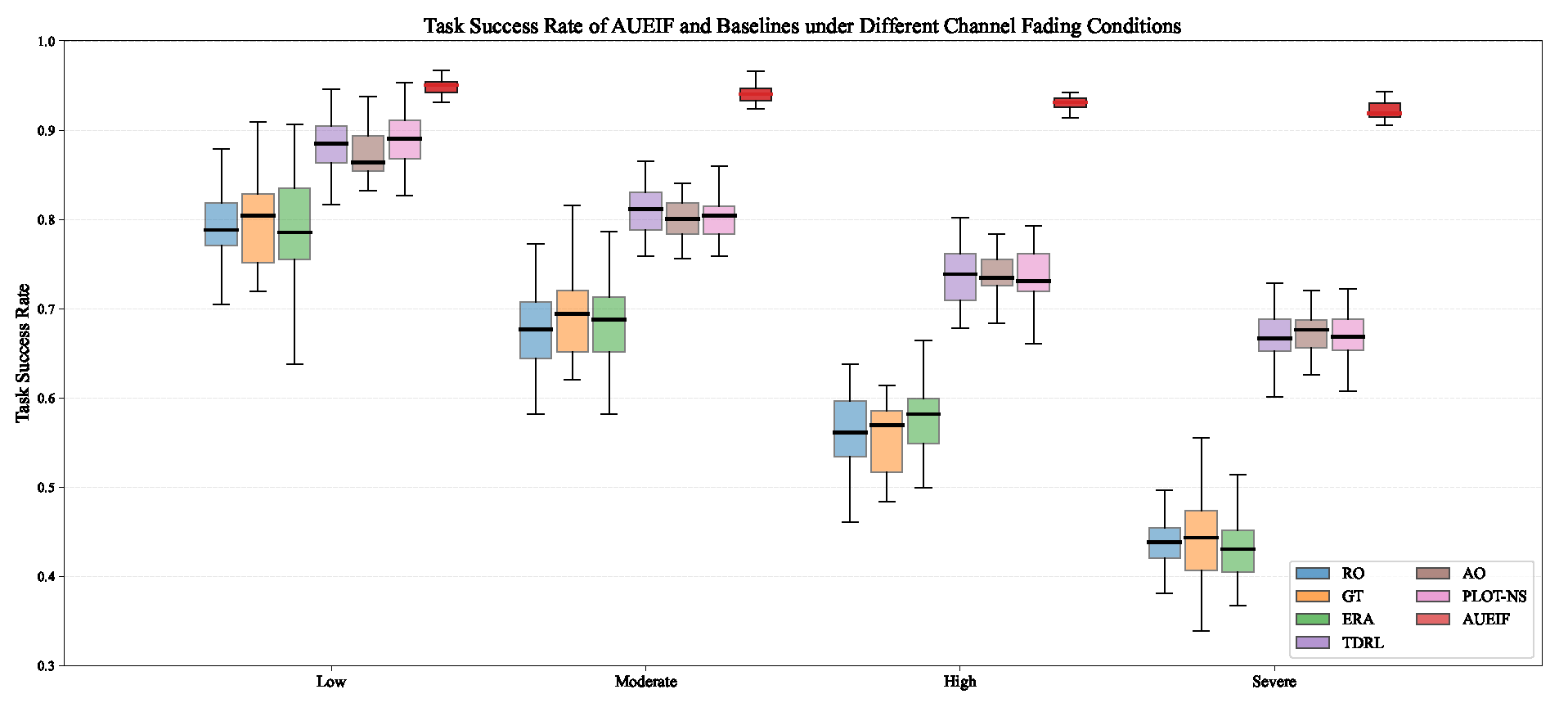
6.5. Robustness of AUEIF Under Varying Channel Fading Conditions

Figure 11 illustrates the distribution of task success rates achieved by the AUEIF and six baseline methods under four channel fading conditions, namely Low, Moderate, High, and Severe. The horizontal axis represents the fading severity, while the vertical axis denotes the overall task success rate, ranging from 0.3 to 1.0. For each fading level, boxplots corresponding to different algorithms are horizontally offset for clarity. Each box indicates the interquartile range (IQR), the central line denotes the median over multiple runs, and the whiskers represent the extrema within 1.5 × IQR. The median performance of the AUEIF is highlighted for visual emphasis.

Across all fading conditions, the AUEIF consistently achieves the highest median task success rate with the lowest performance variance, demonstrating strong robustness against channel degradation. Under Low and Moderate fading, the median success rate of the AUEIF remains above $0.94$, substantially outperforming all baseline approaches. As channel fading intensifies to High and Severe levels, the performance of all methods degrades due to increased signal attenuation and heightened air-to-ground channel instability. Nevertheless, the AUEIF maintains a median success rate exceeding $0.92$, indicating stable and reliable decision-making under adverse channel conditions. In contrast, learning-based baselines such as TDRL, AO, and PLOT-NS experience more pronounced performance degradation, with median success rates declining to the $0.72$–$0.80$ range under Severe fading. Heuristic-based strategies (RO, GT, and ERA) exhibit the most severe degradation, with median performance dropping to the $0.50$–$0.60$ range with substantially increased variability.

The superior robustness of the AUEIF can be attributed to two key design features. First, the LSTM-based temporal channel prediction module enables the framework to anticipate fading trends, allowing proactive adjustments in task offloading decisions and UAV trajectory planning before significant link deterioration occurs. Second, the unified hybrid action space facilitates fine-grained control over partial offloading ratios and transmission strategies, thereby stabilizing queue dynamics even under highly volatile channel conditions. By comparison, RO, GT, and ERA lack adaptive mechanisms, TDRL optimizes policies without explicit task reliability awareness, and PLOT-NS is more susceptible to queue–channel coupling effects when perturbed control mechanisms are absent.

7. Conclusions

This paper proposed an AUEIF framework for multi-UAV-assisted mobile edge computing networks to jointly address UAV trajectory planning, computation offloading, and time-varying air–ground channels. By integrating dynamic graph modeling, hierarchical reinforcement learning, and LSTM-based channel prediction, the AUEIF captures spatio-temporal correlations and enables coordinated optimization of mobility, communication, and computation. Simulation results demonstrate that the AUEIF consistently outperforms baseline methods in terms of task completion delay, energy efficiency, and robustness under diverse system loads and channel fading conditions, while ablation studies confirm the necessity of each core component.

Nevertheless, several limitations remain. The current evaluation relies on simulated mobility and channel models, which may not fully reflect complex urban environments. Moreover, the hierarchical learning framework may introduce additional computational overhead as system scale increases, and inaccurate channel prediction under highly unpredictable conditions could affect decision optimality. Future work will explore decentralized multi-agent extensions, more realistic environment modeling, and integration with emerging 5G/6G network slicing mechanisms to facilitate practical deployment.