Building Up Co-Crystals: Structural Motif Consistencies Across Families of Co-Crystals ^†

Abstract

The creation of co-crystals as a route to creating new pharmaceutical phases with modified or defined physicochemical properties is an area of intense research. Much of the current research has focused on creating new phases for numerous active pharmaceutical ingredients (APIs) to alter physical properties such as low solubilities, enhancing processability or stability. Such studies have identified suitable co-formers and common bonding motifs to aid with the design of new co-crystals but understanding how the changes in the molecular structure of the components are reflected in the packing and resulting properties is still lacking. This lack of insight means that the design and growth of new co-crystals is still a largely empirical process with co-formers selected and then attempts to grow the different materials undertaken to evaluate the resulting properties. This work will report on the results of a combination of crystal structure database analysis with computational chemistry studies to identify what structural features are retained across a selection of families of co-crystals with common components. The competition between different potential hydrogen bonding motifs was evaluated using ab initio quantum mechanical calculations and this was related to the commonality in the packing motifs when observed. It is found while the stronger local bonding motifs are often retained within systems, the balance of weaker long-range packing forces gives rise to many subtle shifts in packing leading to greater challenges in the prediction of final crystal structures.

1. Introduction

Modifying the physicochemical properties of active pharmaceutical ingredients (APIs) through the creation of multi-component crystals (i.e., co-crystals and salts) is a rapidly developing field of study [1]. They have been primarily investigated to adjust solubility and so increase bioavailability [2], but other studies have also included increased stability under storage conditions, improved tableting performance, or processability [3,4]. Such studies are often empirically driven with the screening of standard co-formers under a range of experimental conditions used to locate new potential phases before undertaking an evaluation of the physical properties [5]. Co-formers are frequently chosen by consideration of potential supramolecular synthons that could form between the components [6]. Many potential co-formers offer a number of potential supramolecular synthons and it is not always predictable which will form and how these will lead to desirable properties. One route to achieve this understanding is to undertake data mining exercises into the existing crystal structures from families of multi-component crystals with common structural features throughout the set and identify if there are relationships in the component choice and the resulting crystal structures [7,8,9].

Computational chemistry approaches offer key information to aid with these studies as the intermolecular interactions within known crystal structures, predicted crystal structures, or supramolecular motifs can be readily evaluated. Studies into the formation thermodynamics of co-crystal and salts are limited, however, the majority of multi-component crystals are dominated by the enthalpic component [10,11]. An analysis of lattice energy components indicates two or three close contacts dominate the energy. This suggests that an initial screening could be based on the interactions between the components [12]. For this to be effective, suitable bonding motifs need to be identified or predicted for a given system.

Isonicotinamide (INA) and nicotinamide (NA) are frequently used co-formers, both for modification of API’s physicochemical properties [13,14] and as model systems for co-crystallization studies [15,16]. Both INA and NA offer one hydrogen bond donor/acceptor group (CONH₂) and one hydrogen bond acceptor (N_pyr) but in different orientations, this allows for studies into the influence on relative positioning on the final crystal packing. Thus, there are only three potential interactions with suitable hydrogen bond donor groups such as CO₂H or OH groups (Figure 1). Previous studies indicate a preference for the binding between co-formers and the pyridine nitrogen in most co-crystals [17], however, it would be expected for carboxylic acids that the acid… amide motif should be lower in energy as it comprises two hydrogen bonds. It has been shown for the acid…amide interaction in benzoic acid-benzamide co-crystals that the strength of this interaction depends on the nature of the functional groups present [18] and so the changes in the balance between these interactions will be investigated to identify the interplay between the nature of the other functional groups present in the molecule.

2. Computational Methodology

The crystal structures of isonicotinamide and nicotinamide were located in the Cambridge Structural Database (V5.41) [19] using Conquest (V2020.2.0) [20]. The crystal structure analysis (identification of hydrogen bonding, graph set determination, crystal structure similarity matching) was carried out using Mercury (V2020.2.0) [21,22,23].

Intermolecular hydrogen bonding motifs were identified in the various structures, extracted from the crystal structures, and optimized at the DFT level (TPSS-D/def2-TZVP) [24,25,26,27] using the program orca. The interaction energy for these systems were then evaluated in orca [28] at the DFT (RI-PWPB95-D/ma-def2-QZVPP) [25,29]. The basis set superposition error was evaluated to be ~0.1 kJ mol⁻¹ and so was not included in calculations for tetramers and higher. Energy frameworks for selected crystal structures were evaluated in CrystalExplorer [30] using B3LYP/6-31G(d,p) DFT theory. Pairwise optimization of molecular components was carried out using the drift bias free differential evolution global optimization algorithm (Control parameters: K, F, G_max, N_p = 0.5, 0.98, 5000, 120) [31] using the AA-CLP force field [32] to evaluate the interaction energy between the molecules.

3. Results and Discussion

3.1. Co-Former and Compositional Analysis

A total of 215 isonicotinamide and 158 nicotinamide multi-component crystals were located and grouped based on the functional group hydrogen bonding to the pyridine nitrogen), the numbers of different compositions were also identified (

Table 1. Number of INA containing systems for a given linking motif in different compositions (Co-former:INA) ratio.

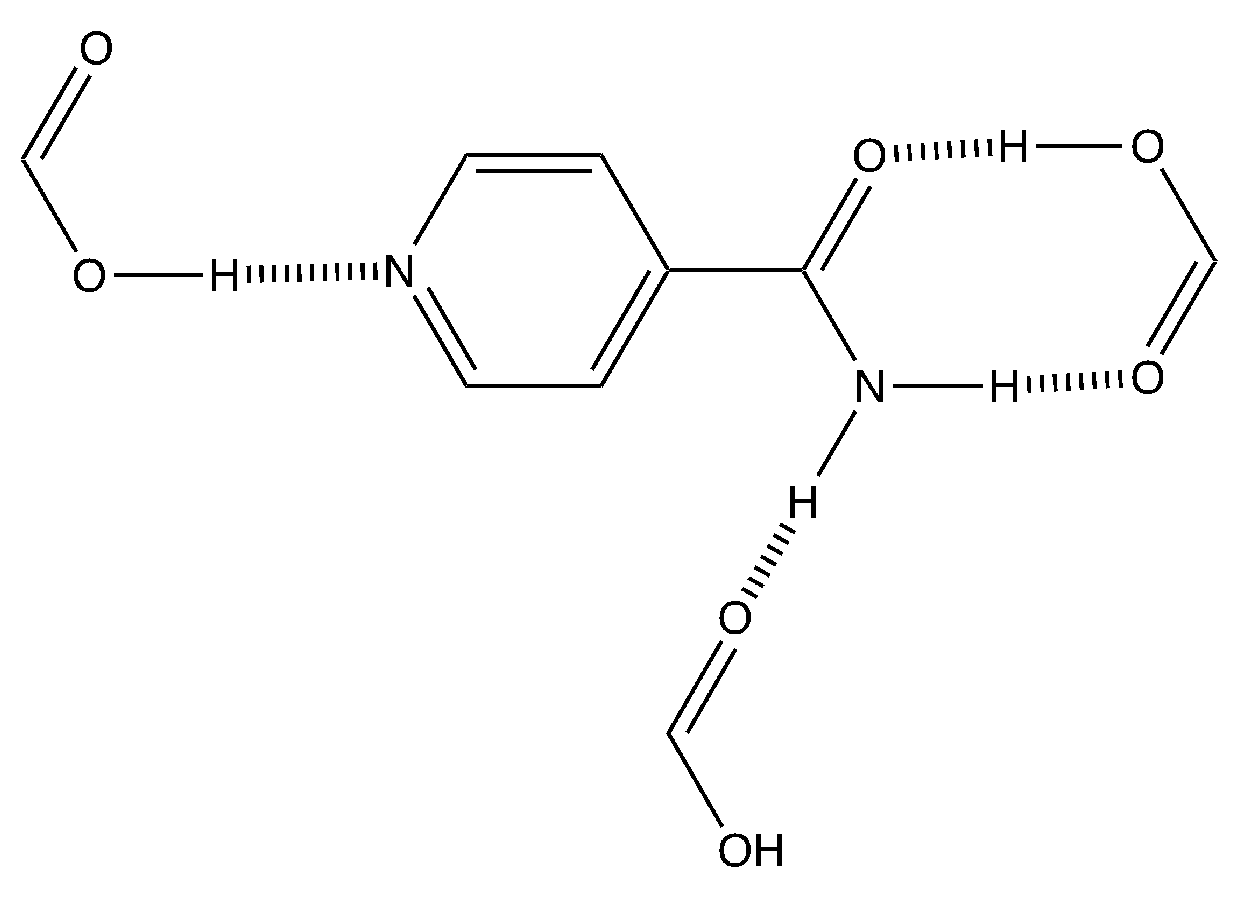
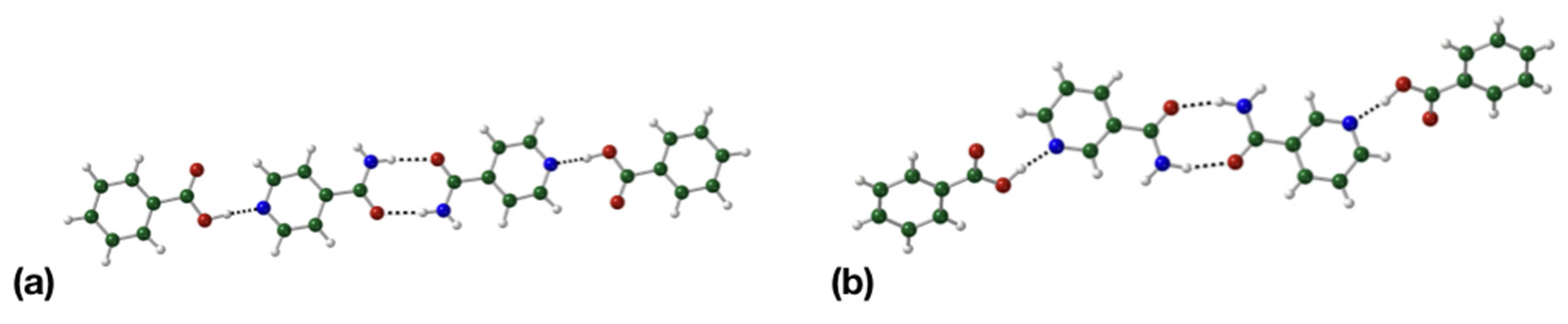
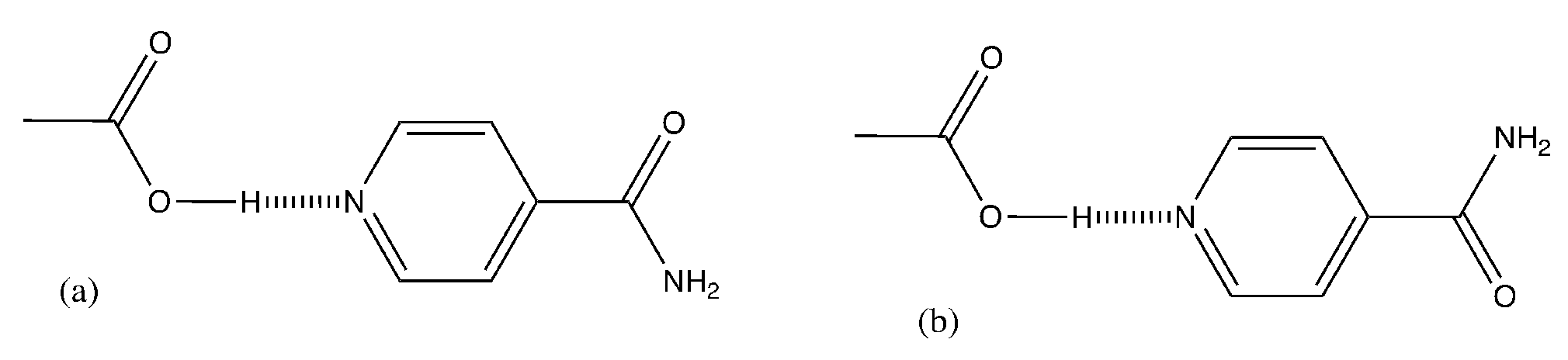
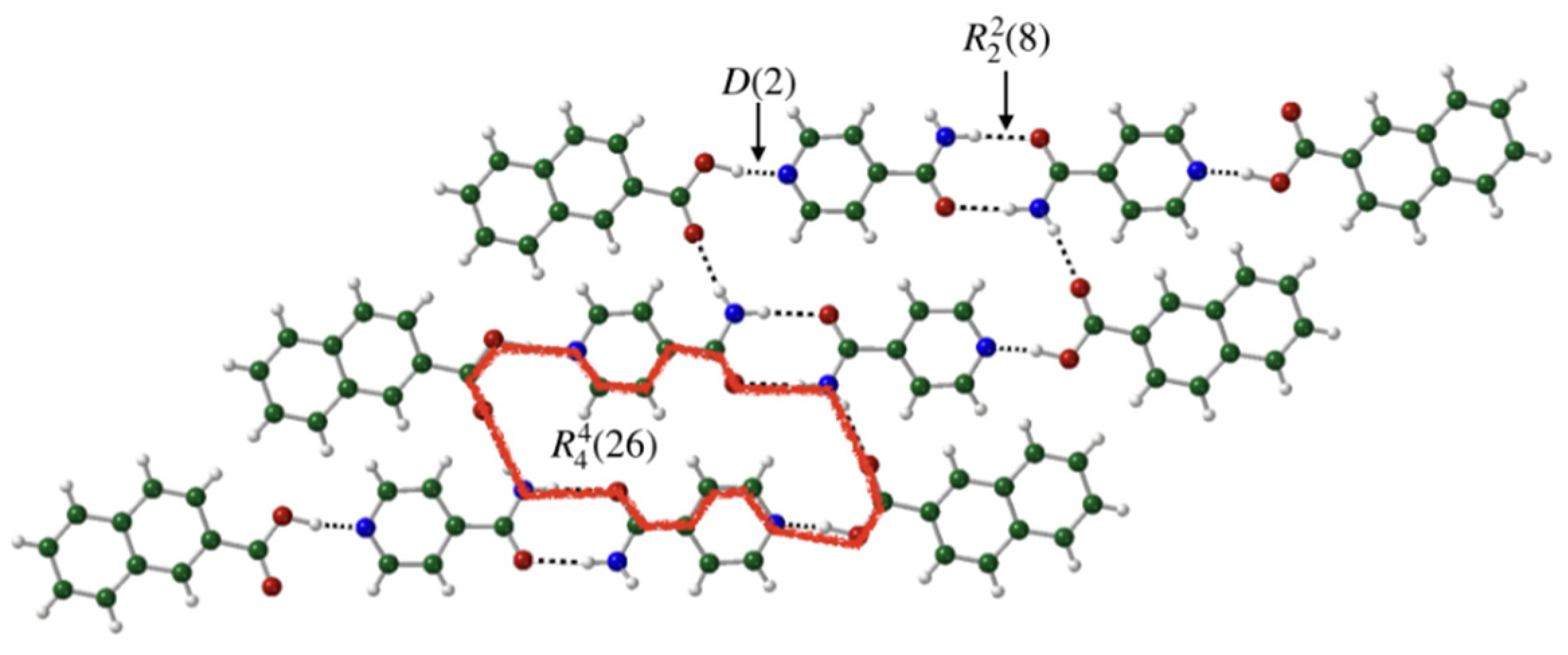
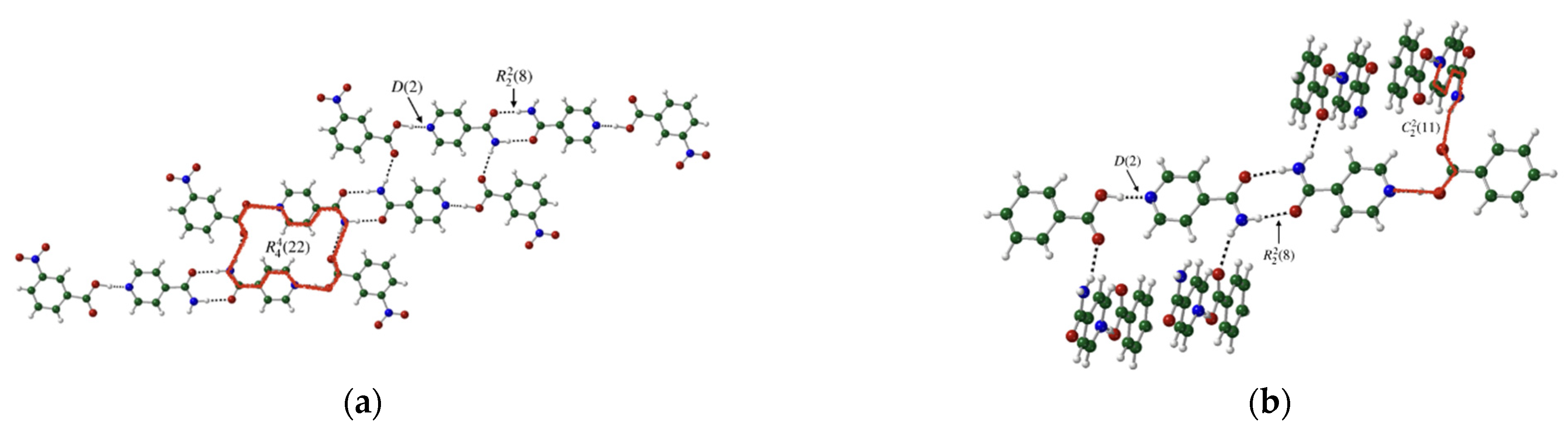
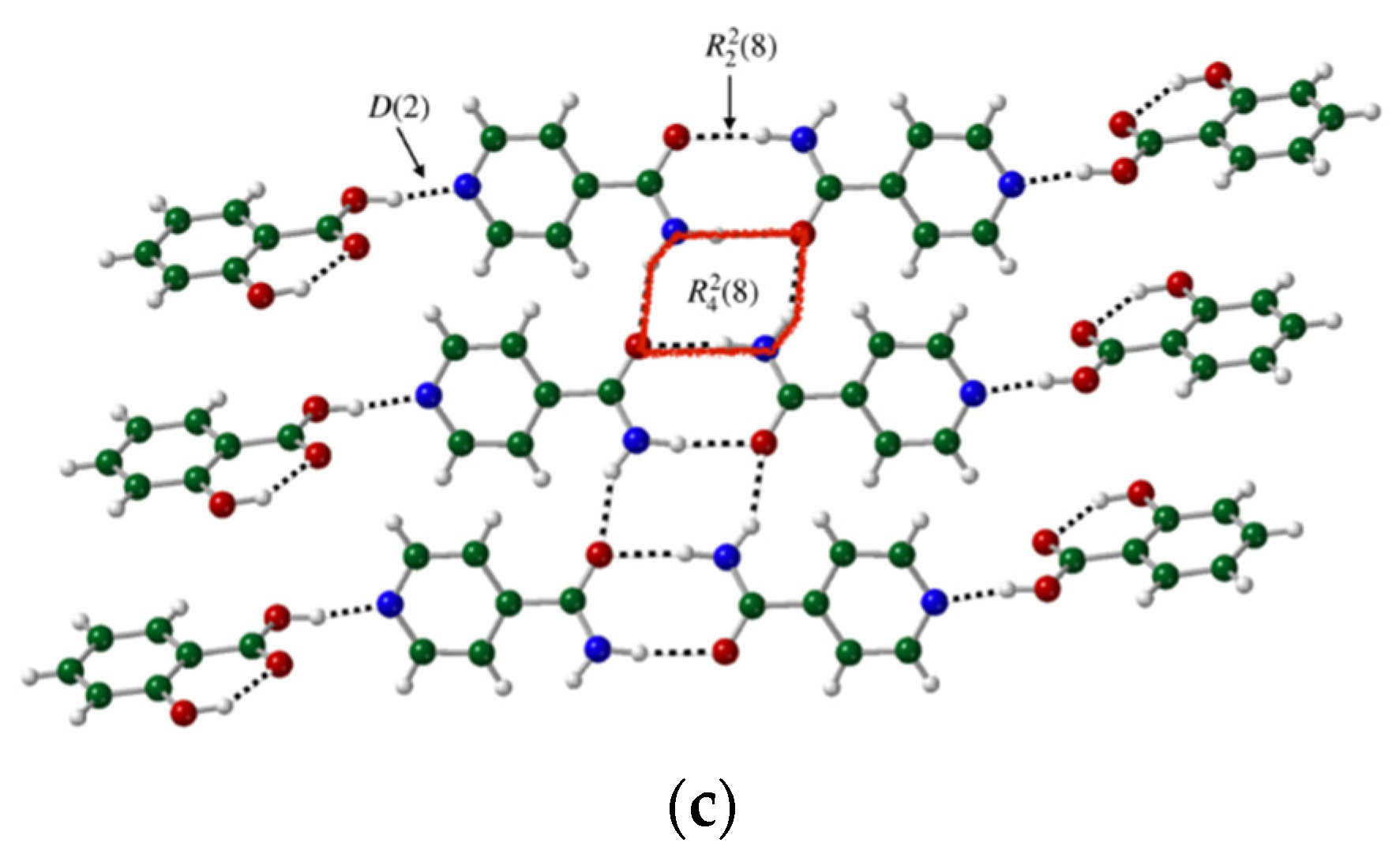
Class	(1:1)	(2:1)	(1:2)	(1:1:1)	Other Compositions §	Totals
ArCO2H…INA	44	9	5	15	1	74 (34%)
RCO2H…INA	44	3	22	2	0	71 (33%)
ROH…INA	18	1	10	1	4	34 (16%)
Other Functional Groups	22	2	4	6	2	36 (17%)
Totals	128 (60%)	15 (7%)	41 (19%)	24 (11%)	7 (3%)	215

^§ Compositions are (1:1:1:1), (1:2:1.7), (1:3:2), (1:2:2), (3:2), (2:1:2).

and

Table 2. Number of NA containing systems for a given linking motif in different compositions (Co-former:INA) ratio.

Class	(1:1)	(2:1)	(1:2)	(1:1:1)	Other Compositions §	Totals
ArCO2H…NA	30	3	3	10	3	49 (31%)
RCO2H…NA	27	3	9	5	4	48 (30%)
ROH…NA	17	2	6	2	6	33 (21%)
Other Functional Groups	16	1	3	4	4	28 (18%)
Totals	90 (58%)	9 (6%)	21 (13%)	21 (13%)	17 (10%)	158

^§ Compositions are (1:3), (1:4), (1:1:2), (1:1:5), (1:2:1), (1:4:1), (2:2:1), (2:2:1.25), (2:4:1), (4:4:3), (2:1:1:4).

). The results show that the distribution is similar for either co-former. NA systems have a higher proportion of compositions compared to INA, which may be due to the relative bent geometry of NA functional compared to the linear location in INA. There appears to be a preference for (1:1) compositions, but this may reflect the screening approaches used and the higher composition systems may be harder to grow compared to the (1:1) composition. It has been reported that the (2:1) benzoic acid-INA co-crystal is metastable compared to the (1:1) and only forms under limited experimental conditions [15,33].

The competition between functional groups was evaluated by considering the types of potential hydrogen bond donor groups present in the co-formers and the relative compositions formed (

Table 3. Numbers of Hydrogen Bond Donating Functional Groups Present in Different Compositions of INA/NA Co-Crystals. The first group in pair bonds to the pyridine N.

Groups—INA	(1:1)	(2:1)	(1:2)	Groups—NA	(1:1)	(2:1)	(1:2)
CO2H	69	6	22	CO2H	36	4	11
CO2H/OH	13	4	4	CO2H/OH	14	2	1
CO2H/NH2	6	1	0	CO2H/NH2	3	0	0
CO2H/CONHR	1	1	0	CO2H/CONHR	1	0	0
CO2H/SO2NH2	0	1	0	CO2H/SO2NH2	2	0	1
OH	14	1	10	OH	15	1	4
OH/CO2H	3	0	0	OH/CO2H	2	0	0
OH/CONHR	2	0	0	OH/CONHR	0	0	1
CONH2	4	1	0	CONH2	2	1	2
SO2NHR/CO2H	1	0	1	SO2NHR	3	0	0
NH2	5	0	0	NH2	3	0	0
All other functional groups	10	0	4	All other functional groups	8	0	1

). Single functional group types form the majority of systems and dominate the (1:1) composition systems as expected. The (1:2) composition systems are dominated by molecules with multiple functional groups as 37/41 INA systems and 14/20 NA systems are classified as such. In contrast, the (2:1) systems generally have a single functional group present and both groups bind to different sites on the INA/NA molecules.

3.2. Crystal Packing Analysis

The (1:1) systems were selected for further analysis to identify repeating patterns in the bonding. Polymorphic systems were counted as separate systems as the hydrogen bonding motifs could be different in the different phases. First level graph set patterns were generated for each system (

Table 4. Frequencies of 1st level graph set motifs for INA and NA (1:1) co-crystals ^§.

System	D(2)R22(8)	D(2)R22(x)	D(2)	D(2)C(x)
ArCO2H---INA	41	0	2	1
RCO2H---INA	20	0	21	3
ROH---INA	7	5	5	2
Other Functional Groups	9	0	4	10
Totals	77 (59%)	5 (4%)	32 (25%)	16 (12%)
ArCO2H---NA	11	0	7	16
RCO2H---NA	12	0	11	5
ROH---NA	5	0	8	7
Other Functional Groups	7	0	1	8
Totals	35 (36%)	0 (0%)	27 (28%)	36 (36%)

^§ x in graph set symbol indicates variable length of motif.

) to evaluate the differences between the phases.

For INA, the dominant structure is a tetramer motif in 72% of the INA co-crystals (Figure 2a). The remaining systems form a chain motif through two or more functional groups present in the co-former. In contrast, the opposite behavior is observed in NA systems with only 36% of systems forming a tetramer motif (Figure 2b). While the INA examples form planar structures, the motif in NA is twisted (the angle between benzoic acid and INA/NA molecular planes are 6° and 127° respectively). The carboxylic acid-INA systems show shifts in the form of this tetramer with 28% featuring a cis geometry between the carbonyl groups (Figure 3). Polymorphic 2,4,6-trifluorobenzoic acid-isonicotinamide (PIRNOV) displays both geometries in different phases. DFT energy calculations show the trans geometry is lower by 2.15 kJ mol⁻¹. All bar one of the cis based tetramers form a consistent 3rd level hydrogen-bonding motif forming a 1-D ladder structure built from a $R_6^6\left(26\right)$ motif (Figure 4). The exception is form I of 5-chlorosalicylic acid (JIPJEQ) which forms a $C_2^2\left(11\right)$ motif instead. However, none of the 3-D structures display any further packing similarities. Thus, the strongest interactions in the structure may be predictable, but the range of weaker packing forces can lead to a number of different crystal structures.

The majority of trans systems can be classified into three sets: M2 has a 1-D ladder linked through a $R_4^4\left(22\right)$ motif (24/56 systems, Figure 5a), M3 has an interlocked 3-D structure with $C_2^2\left(11\right)$ motifs (23/56 systems, Figure 5b), M4 links into a 1-D ladder through amide…amide ring with a $R_4^2\left(8\right)$ motif (4/56 systems, Figure 5c). The M2 set has three isostructural sets of structures, while 15 M3 structures pack in an isostructural set of C2/c structures, typified by benzoic acid (Figure 5b). The remaining groups have flatter angles. The M4 set splits into two isostructural subsets. This again confirms consistent local bonding but differences in the longer-range packing.

3.3. Binding Interactions

The energy of intermolecular interactions within the (1:2) dicarboxylic acid-INA co-crystals were evaluated within CrystalExplorer. Summing the three strongest interactions in the structure (INA^…INA, N-H^…O=C, CO₂H^…N_pyr)) shows a general decrease with increasing chain length, however, a slight odd-even alternation is noted (Figure 6). Comparing this to the reported melting point shows a complementary pattern. However, the trend is not perfectly matched; there are two reported values for the melting point of the succinic acid co-crystal (135 °C [34] and 206 °C [35]) which affects the curves. Optimization of the position and orientation of molecules of oxalic acid with INA links the molecules through an acid^…amide bond. This motif is not observed in any of the oxalic co-crystal structures but is lower in energy than the observed motif (

Table 5. Energetics of acid…INA interactions at (RI-PWPB95-D/ma-def2-QZVPP) level of theory.

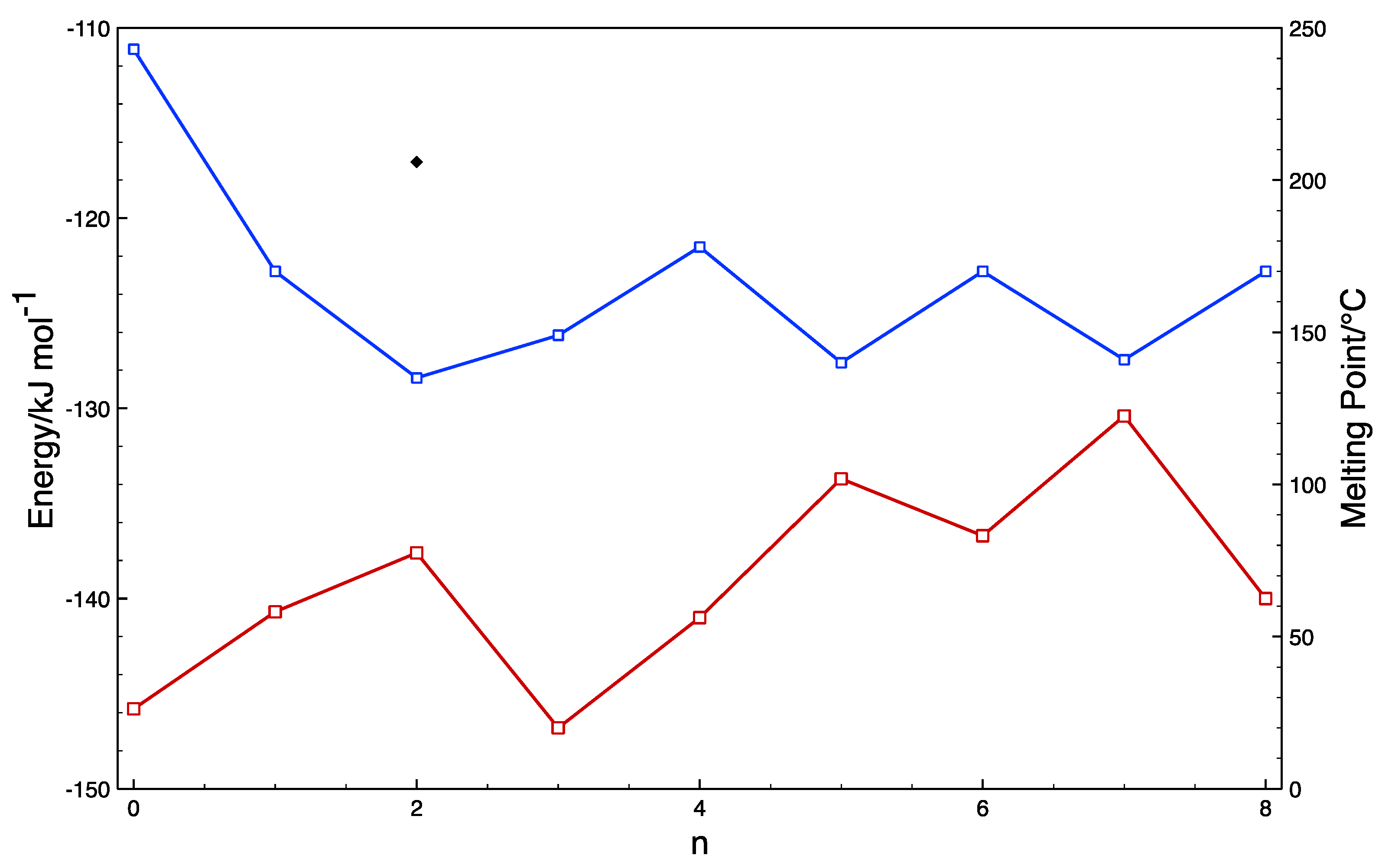
System	Acid…Amide Motif kJ mol−1	Acid…Npyr Motif kJ mol−1	Difference kJ mol−1
Oxalic acid	−36.145	−32.556	−3.589
Malonic acid	−67.531	−51.742	−15.789
Succinic acid	−60.365	−45.143	−17.814
Glutaric acid	−61.957	−44.143	−16.959
Adipic acid	−57.152	−40.193	−16.959
Pimelic acid	−57.793	−50.027	−7.765
INA	−56.703	N/A	N/A

). Evaluation of formation energy for the tetramer over two acid^…amide dimers for a model system shows that the tetramer is favored energetically by −26.74 kJ mol⁻¹. Thus, a set of slightly weaker interactions can give overall increased energy compared to the utilization of strongest possible interaction at each point. Similar evaluations for NA systems show similar energy values to INA ones and so the difference in packing appears to be dominated by the geometry and packing forces rather than preferential energetics between the molecules.

4. Conclusions

INA co-crystals and salts show consistent bonding features in the resulting crystal structures, with a common tetramer forming 72% of cases; in contrast, NA only forms this motif in 36% of structures. Evaluation of the energy of the hydrogen bonds shows that in INA, while the stronger individual interactions can be predicted, the combination of motifs in the tetramer gives a lower overall energy. This highlights that the balance between numerous factors dominates the co-crystallization processes. INA and NA systems have similar energy values and so the differences in packing appear to be driven by the ability to pack efficiently in the crystal form rather than energetically. This indicates that to develop predictive methods based on pointwise contact location of the range of possibilities is more important compared to the location of the global minimum interaction and evaluation of potential higher-order building blocks will give insights into the resulting properties of the materials.