Predictivity of CNC Machine-Induced Vibrations on Inter-Story Floors Based on Coupled Experimental-Numerical Investigations †
Abstract
:1. Introduction
1.1. Motivation
1.2. Reference Stantards
2. Experimental and Numerical Study
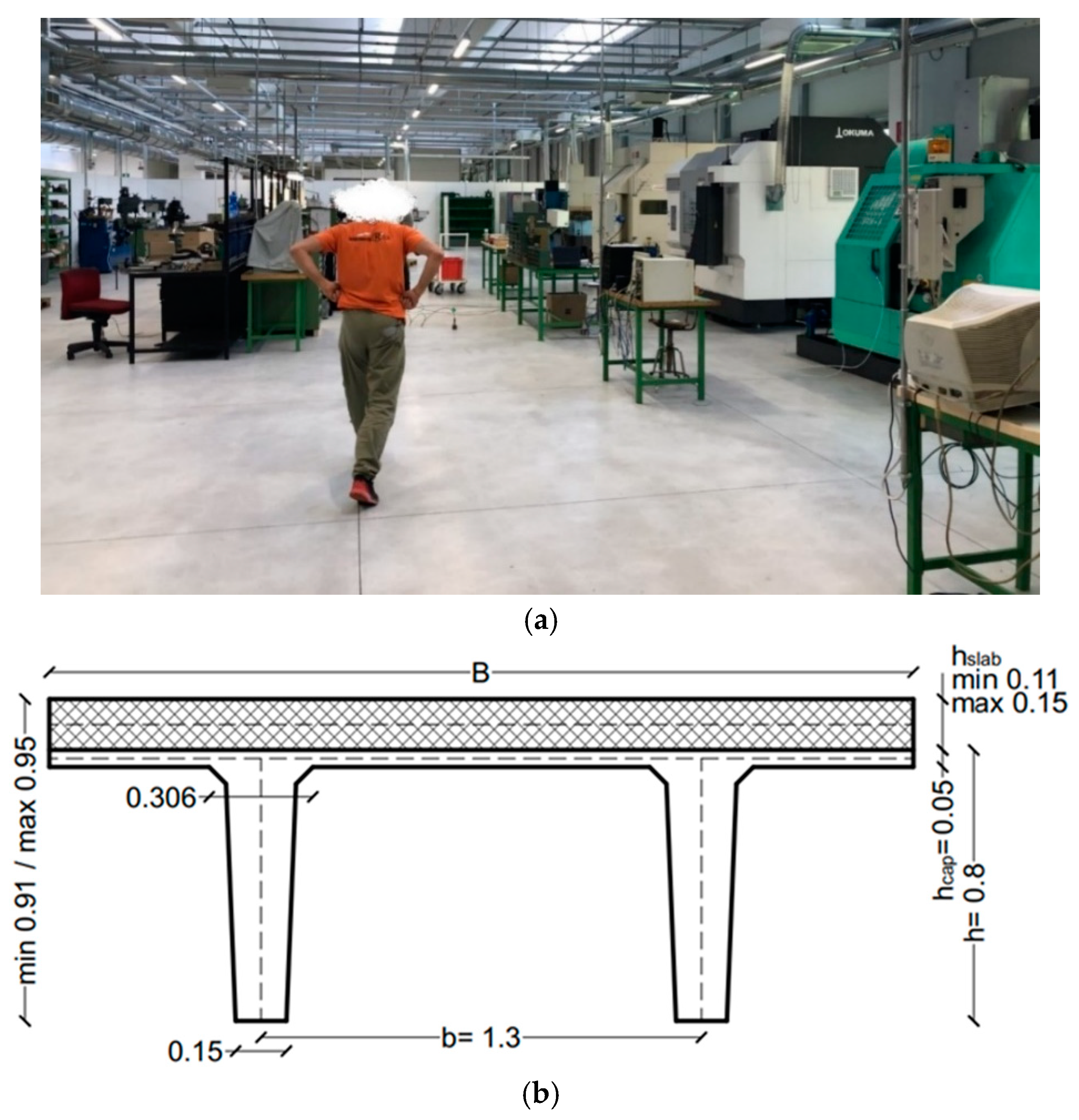
2.1. Case-Study Building
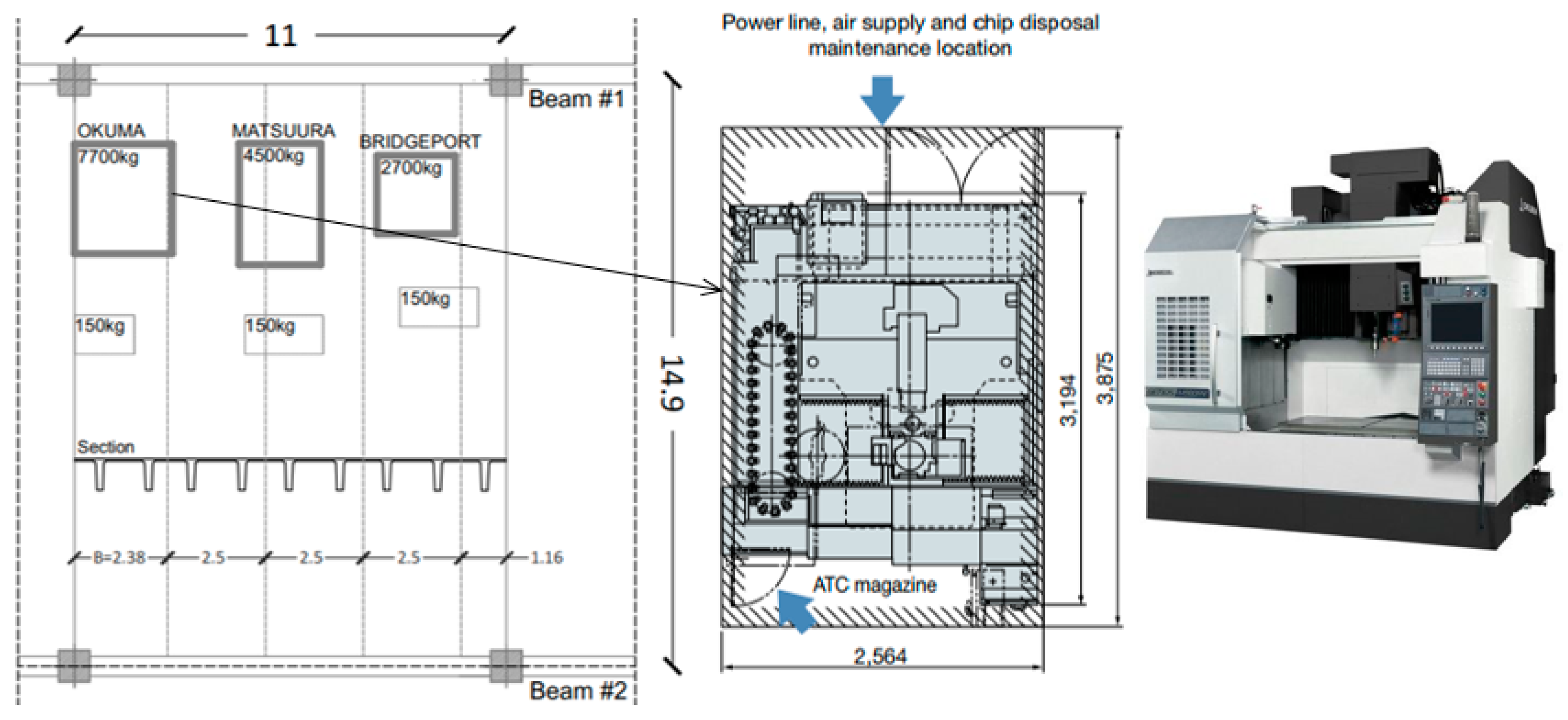
2.2. CNC Machines
2.3. Experimental Methods
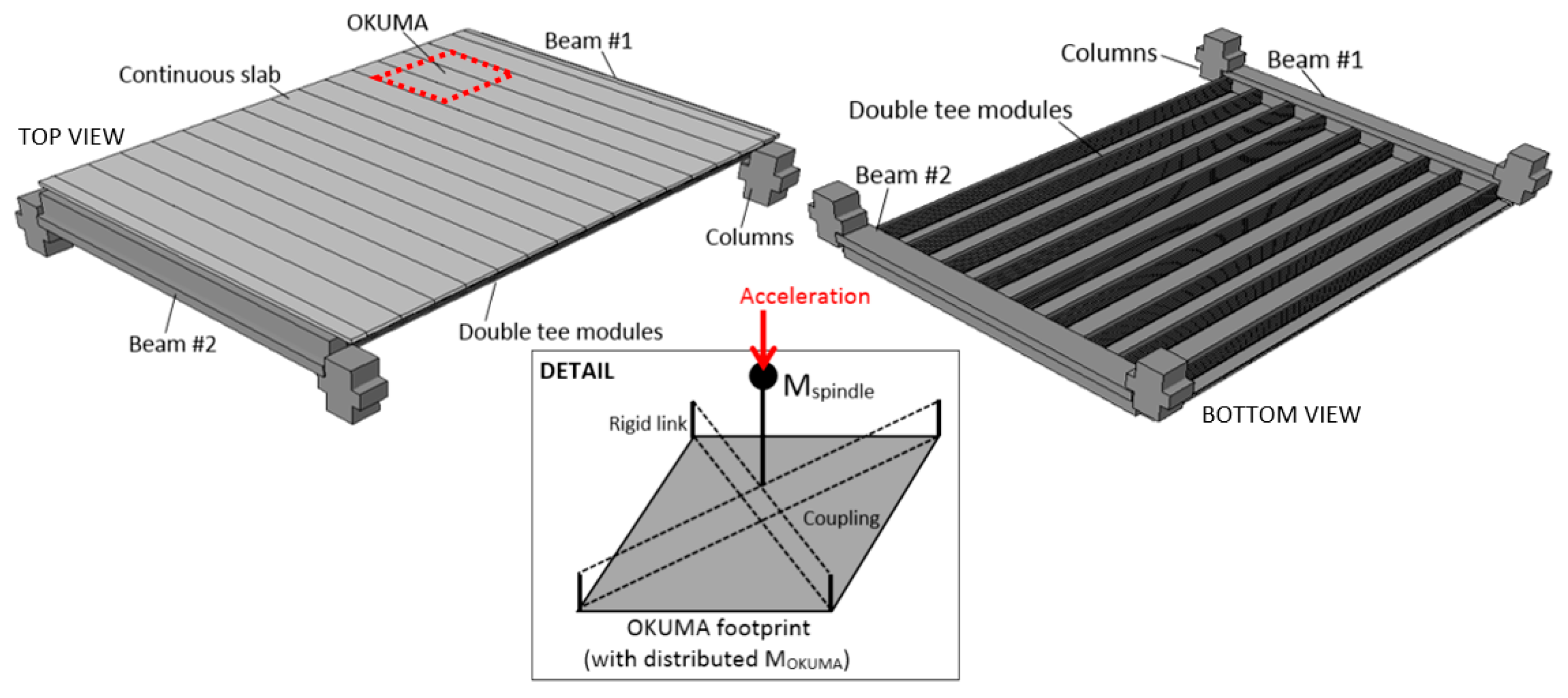
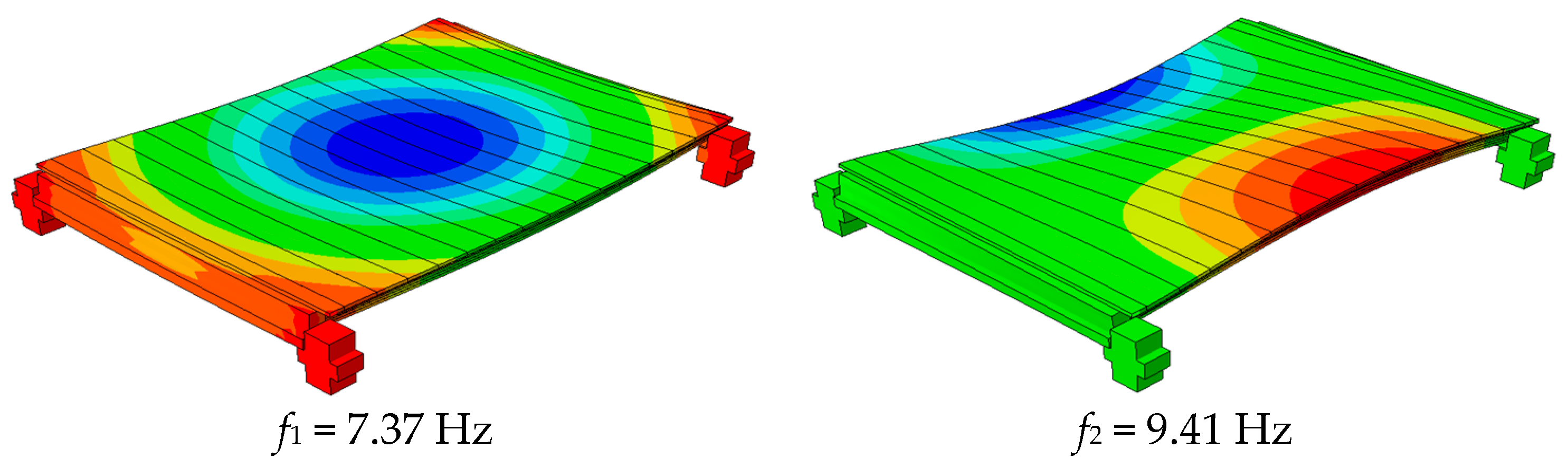
2.4. Finite Element Numerical Model
3. Discussion of Results
3.1. CNC Machinery Center and Inter-Story Floor Measurements
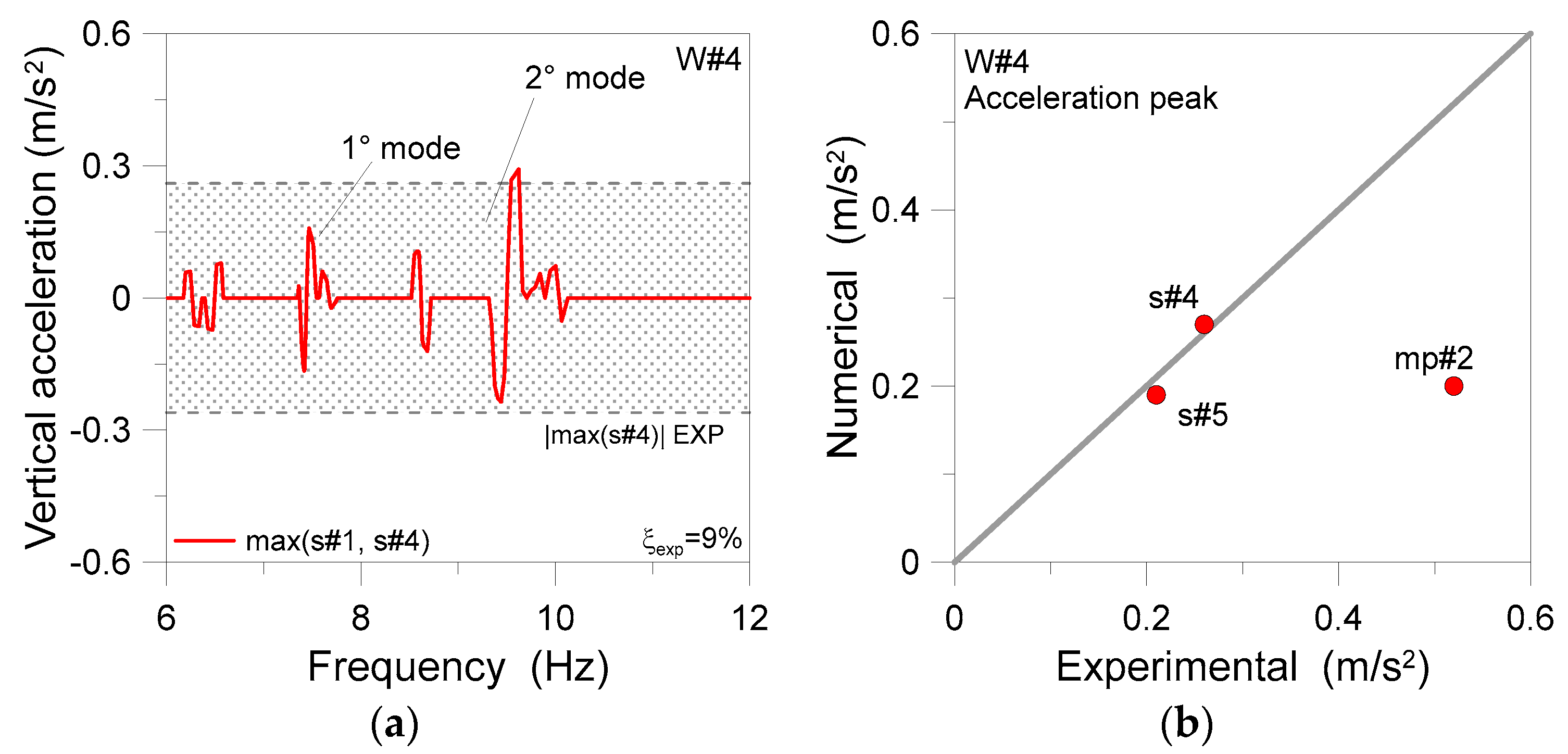
3.2. Validation of the Coupled Experimenta-Numerical Procedure
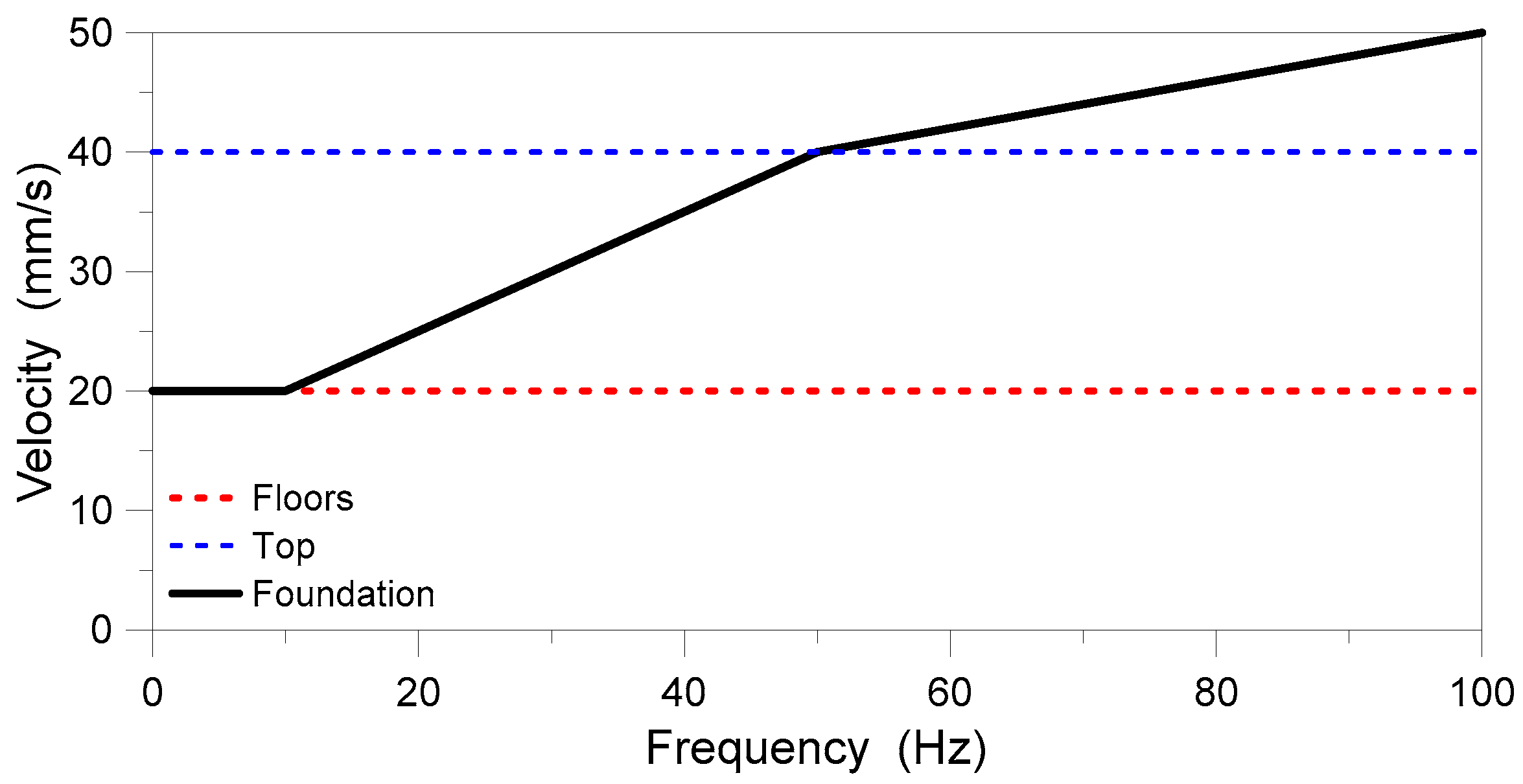
3.3. Vibration Serviceability Assessment
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| CNC | computer numerical control |
| DAF | dynamic amplification factor |
| FE | finite element |
| MEMS | micro electro-mechanical systems |
| MoE | modulus of elasticity |
References
- Bachmann, H.; Ammann, W. Vibrations in Structures Induced by Man and Machines; IABSE-International Association for Bridge and Structural Engineering: Zurich, Switzerland, 1987; ISBN 3-85748-052-X. [Google Scholar]
- Feldmann, M.; Heinemeyer, C.; Butz, C.; Caetano, E.; Cunha, A.; Galanti, F.; Goldack, A.; Hechler, O.; Hicks, S.; Keil, A.; et al. Design of Floor Structures for Human Induced Vibrations; Technical Report EUR 24084 EN; Publications Office of the European Union: Bruxelles, Belgium, 2009; ISBN 978-92-79-14094-5. [Google Scholar] [CrossRef]
- Da Silva, J.G.S.; Sieira, A.C.C.F.; Da Silva, L.A.P.S.; Rimola, B.D. Dynamic Analysis of Steel Platforms When Subjected to Mechanical Equipment-Induced Vibrations. J. Civ. Eng. Arch. 2016, 10, 1103–1113. [Google Scholar] [CrossRef]
- Brownjohn, J.; Pavic, A. Vibration control of ultra-sensitive facilities. Proc. Inst. Civ. Eng. Struct. Build. 2006, 159, 295–306. [Google Scholar] [CrossRef]
- Chang, M.-L.; Lin, C.-C.; Ueng, J.-M.; Hsieh, K.-H.; Wang, J.-F. Experimental study on adjustable tuned mass damper to reduce floor vibration due to machinery. Struct. Control Health Monit. 2009, 17, 352–548. [Google Scholar] [CrossRef]
- Kazantzi, A.K.; Vamvatsikos, D. Seismic and Vibration Performance Rehabilitation for an Industrial Steel Building. Pract. Period. Struct. Des. Constr. 2020, 25, 05020001. [Google Scholar] [CrossRef]
- Wilson, R.R. Machine Foundations. In Vibrations of Engineering Structures; Lecture Notes in Engineering; Springer: Berlin/Heidelberg, Germany, 1985; Volume 10. [Google Scholar] [CrossRef]
- Tian, Y.; Liu, Z.; Xu, X.; Wang, G.; Li, Q.; Zhou, Y.; Cheng, J. Systematic review of research relating to heavy-duty machine tool foundation systems. Adv. Mech. Eng. 2019, 11. [Google Scholar] [CrossRef]
- Stimac, G.; Braut, S.; Zigulic, R. Structural optimization of turbine generator foundation with frequency constraint. Strojarstvo 2011, 53, 389–398. [Google Scholar]
- Liu, J.B.; Wang, Z.Y.; Zhang, K.F.; Pei, Y.X. 3D Finite element analysis of large dynamic machine foundation considering soil-structure interaction. Eng. Mech. 2002, 19, 34–35. [Google Scholar]
- Tian, Y.; Shu, Q.; Liu, Z.; Ji, Y. Vibration Characteristics of Heavy-Duty CNC Machine Tool-Foundation Systems. Shock Vib. 2018, 2018. [Google Scholar] [CrossRef]
- Werner, U. Derivation of a plane vibration model for electrical machines on soft machine foundations. Forsch. Ing. 2010, 74, 185–205. [Google Scholar] [CrossRef]
- Bergamo, E.; Fasan, M.; Bedon, C. Efficiency of Coupled Experimental–Numerical Predictive Analyses for Inter-Story Floors Under Non-Isolated Machine-Induced Vibrations. Actuators 2020, 9, 87. [Google Scholar] [CrossRef]
- ABAQUS Computer Software; Simulia: Providence, RI, USA, 2020.
- Bedon, C.; Bergamo, E.; Izzi, M.; Noé, S. Prototyping and Validation of MEMS Accelerometers for Structural Health Monitoring-The Case Study of the Pietratagliata Cable-Stayed Bridge. J. Sens. Actuator Netw. 2018, 7, 30. [Google Scholar] [CrossRef]
- Brand, T. Demands on Sensors for Future Servicing: Smart Sensors for Condition Monitoring. 2017. Available online: https://www.analog.com/media/en/technical-documentation/tech-articles/A60151-Demands-on-Sensors-for-Future-Servicing-Smart-Sensors-for-Condition-Monitoring.pdf (accessed on 7 November 2020).
- Cizikova, A.; Monkova, K.; Monka, P.; Moravec, M. Analysis of frequency characteristics at spindle of CNC machining centre. MM Sci. J. 2016, 2016, 1515–1518. [Google Scholar] [CrossRef]
- Abdulhani, F.; Alswede, J. Study of vibration for CNC machine at different feed. Int. J. Adv. Res. Technol. 2014, 3, 21–29. [Google Scholar]
- Dogrusoz, H.; Wszolek, G.; Czop, P.; Sloniewski, J. Vibration monitoring of CNC machinery using MEMS sensors. J. Vibroeng. 2020, 22, 735–750. [Google Scholar] [CrossRef]
- Eurocodice 4—Progettazione Delle Strutture Composte Acciaio-Calcestruzzo-Parte 1-1: Regole Generali e Regole per Gli Edifici; UNI EN 1994-1-1:2004; Ente Nazionale Italiano di Unificazione (UNI): Milan, Italy, 2005.
- Ministero delle Infrastrutture e dei Trasporti-DM 17/01/2018. Norme Tecniche per le Costruzioni (NTC2018). 2018.
- Ministero delle Infrastrutture e dei Trasporti-Circolare n.7 del 21/01/2019-Istruzioni per l’applicazione dell’ “Aggiornamento delle Norme Tecniche per le Costruzioni”. 2019.
- Criteri di Misura e Valutazione Degli Effetti Delle Vibrazioni Sugli Edifici; UNI9916: 2014; Ente Nazionale Italiano di Unificazione (UNI): Milan, Italy, 2014.
- OKUMA Europe GmbH. Available online: www.okuma.eu (accessed on 27 July 2020).
- MATSUURA Machinery Corporation. Available online: https://www.matsuura.co.jp/english/ (accessed on 27 July 2020).
- BRIDGEPORT Machines. Available online: https://www.hardinge.com/product-brand/bridgeport/ (accessed on 27 July 2020).




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bergamo, E.; Fasan, M.; Bedon, C. Predictivity of CNC Machine-Induced Vibrations on Inter-Story Floors Based on Coupled Experimental-Numerical Investigations. Proceedings 2020, 64, 15. https://doi.org/10.3390/IeCAT2020-08529
Bergamo E, Fasan M, Bedon C. Predictivity of CNC Machine-Induced Vibrations on Inter-Story Floors Based on Coupled Experimental-Numerical Investigations. Proceedings. 2020; 64(1):15. https://doi.org/10.3390/IeCAT2020-08529
Chicago/Turabian StyleBergamo, Enrico, Marco Fasan, and Chiara Bedon. 2020. "Predictivity of CNC Machine-Induced Vibrations on Inter-Story Floors Based on Coupled Experimental-Numerical Investigations" Proceedings 64, no. 1: 15. https://doi.org/10.3390/IeCAT2020-08529
APA StyleBergamo, E., Fasan, M., & Bedon, C. (2020). Predictivity of CNC Machine-Induced Vibrations on Inter-Story Floors Based on Coupled Experimental-Numerical Investigations. Proceedings, 64(1), 15. https://doi.org/10.3390/IeCAT2020-08529





