SU-QMI: A Feature Selection Method Based on Graph Theory for Prediction of Antimicrobial Resistance in Gram-Negative Bacteria ^†

Abstract

Machine learning can be used as an alternative to similarity algorithms such as BLASTp when the latter fail to identify dissimilar antimicrobial-resistance genes (ARGs) in bacteria; however, determining the most informative characteristics, known as features, for antimicrobial resistance (AMR) is essential to obtain accurate predictions. In this paper, we introduce a feature selection algorithm called symmetrical uncertainty qualitative mutual information (SU-QMI), which selects features based on estimates of their relevance, redundancy, and interdependency. We use these together with graph theory to derive a feature selection method for identifying putative ARGs in Gram-negative bacteria. We extract physicochemical, evolutionary, and structural features from the protein sequences of five genera of Gram-negative bacteria—Acinetobacter, Klebsiella, Campylobacter, Salmonella, and Escherichia—which confer resistance to acetyltransferase (aac), β-lactamase (bla), and dihydrofolate reductase (dfr). Our SU-QMI algorithm is then used to find the best subset of features, and a support vector machine (SVM) model is trained for AMR prediction using this feature subset. We evaluate performance using an independent set of protein sequences from three Gram-negative bacterial genera—Pseudomonas, Vibrio, and Enterobacter—and achieve prediction accuracy ranging from 88 to 100%. Compared to the SU-QMI method, BLASTp requires similarity as low as 53% for comparable classification results. Our results indicate the effectiveness of the SU-QMI method for selecting the best protein features for AMR prediction in Gram-negative bacteria.

1. Introduction

Thousands of people in the United States die each year due to infections by antimicrobial-resistant bacteria [1,2]. Convergent evolution or ancient divergence can lead to genes in different organisms that encode proteins with related structure and function, but with limited sequence similarity. Consequently, when new antimicrobial-resistance genes (ARGs) emerge in a population, it may be difficult or impossible to recognize these genes based on conventional sequence similarity algorithms. Sequence matching algorithms such as BLASTp can be applied to find ARGs in bacterial genomes; however, such algorithms do not work well for dissimilar sequences unless very relaxed matching criteria are used, but this leads to inclusion of many potential false positives [3]. Machine learning algorithms are not restricted to sequence similarity, and thus, a machine learning method is a promising alternative for identifying unrecognized ARGs in bacteria. The development of a machine learning algorithm capable of accurate prediction of AMR involves identifying and using the most important features from known ARGs and non-ARGs. In this work, we introduce a graph-theoretic feature selection algorithm called symmetrical uncertainty qualitative mutual information (SU-QMI) in which a feature is selected based on estimates of its relevance, nonredundancy, and interdependency. SU-QMI is based on the concepts of symmetrical uncertainty [4], qualitative mutual information [5], and graph theory for predicting AMR in Gram-negative bacteria. Symmetrical uncertainty (SU) measures the division of information between two features w.r.t. all their information. The qualitative mutual information (QMI) of a feature is the product of its qualitative score and the information it contributes to classification. Graph theory is the study of the relationships among objects (nodes), where the objects are connected by links (edges). In our case, the objects are features. A support vector machine (SVM) model is developed for predicting putative ARGs using the feature subset obtained by means of the SU-QMI algorithm. The performance of our work is compared with another feature selection method—RReliefF [6], which also considers feature interactions—to show the effectiveness of SU-QMI. In addition, the performance of our machine learning model is compared with BLASTp results.

2. Material and Methods

2.1. Data Collection

We considered the same datasets described in [3]. To summarize, we gathered 33, 43, and 28 ARGs from Acinetobacter, Klebsiella, Campylobacter, Salmonella, and Escherichia, which confer resistance to acetyltransferase (aac), β-lactamase (bla), and dihydrofolate reductase (dfr), respectively. We also collected 71 non-ARGs (64 essential genes and 7 histone acetyltransferases) from these Gram-negative bacteria. These ARG (positive) and non-ARG (negative) datasets were used to train our machine learning model. To measure the predictive power of our final classifier, we used 10 aac, 43 bla, and 8 dfr ARGs and 33 non-ARGs (25 essential genes and 8 histone acetyltransferases) from the three Gram-negative bacterial genera Pseudomonas, Vibrio, and Enterobacter as the test datasets.

2.2. Protein Features

We considered a 621D feature vector for each protein sequence, as described in [3,7,8]. Briefly, we created a 20D (‘D’ means dimension) amino acid composition feature vector where each of the 20 feature values is the fraction of a particular amino acid in a protein sequence. The composition, transition, and distribution (CTD) model [9] is used to generate 168D global physicochemical features from a protein sequence. We obtained 400D features from the position-specific scoring matrix (PSSM); this feature vector was computed based on the transition scores between neighboring amino acids in a sequence. Finally, 33D features were obtained from the secondary structure and structure probability matrix of the sequences.

2.3. Feature Selection

Our feature selection algorithm is based on the concepts of SU, QMI, and graph theory. SU measures the relevance between features f_i (i = 1, 2, …, n), and the class C where n is the total number of features. The relevance is calculated using Equation (1) where I and H are mutual information and entropy, respectively. SU provides a normalized relevance value to resist the bias of features having large values.

$$RV(f_i,C)=2\frac{I(f_i,C)}{H(f_i)+H(C)}$$

(1)

QMI is estimated from the product of the utility function U and mutual information. The utility function U is the feature importance. The “Mean Decrease Gini” of a feature w.r.t. class C using a random forest model is estimated to determine feature importance. The Gini index (GI) [10] indicates the homogeneity of the data. Low and high GI values correspond to high homogeneity and high heterogeneity, respectively. The higher the “Mean Decrease Gini”, the greater the feature importance. Thus, the normalized redundancy or interdependency ratio RI(f_i, f_j) between two features f_i and f_j is computed as follows:

$$RI(f_i,f_j)=2\frac{I(f_i;C|f_j)-U_i\times I(f_i;C)}{H(f_i)+H(C)},i=1,2,\cdots ,n;j=1,2,\cdots ,n;i\ne j$$

(2)

Here, I(f_i; C|f_j) is the conditional mutual information shared by f_i and C when f_j is given, and U_i is the feature importance of feature f_i. RI(f_i, f_j) > 0 indicates feature interdependency.

Algorithm 1 gives the details of our SU-QMI feature selection method. We consider a complete graph G = (V, E), where V is the set of all features and E is the set of edges denoting the normalized interdependency or redundancy values between nodes (features). Suppose we have a node set F = {f₁, f₂, ⋯, f_n} and we want to select k nodes from F. Initially, equal weights are assigned to each node (line 2). The node having the highest normalized relevance value is selected first and is placed in the queue Q where the maximum length of Q can be k (lines 3–5). Next, we calculate the scores of the remaining nodes using the relevance, redundancy/interdependency values, and weights of the selected nodes (lines 6–14). The score of a candidate feature f_s is calculated using Equation (3), where W_qi is the weight of the selected node q_i.

Algorithm 1: SU-QMI algorithm

Input: A complete graph G = (V, E) where V is the set of all features and E denotes the edges representing the normalized interdependency or redundancy value between vertices (features), feature set F, class C, number of features to be selected k, and queue Q.

Output: Best feature subset Q

$$score(f_s)=RV(f_s,C){\displaystyle \sum _{q_i\in Q}RI(f_s,q_i)}{W}_{q_i}$$

(3)

Weights are calculated to give more weight to the node selected prior to the other nodes that are chosen. The weight W_qi is calculated using the rank order centroid method [11], as shown in Equation (4), where r_j is the rank of the j-th nodes of Q, and t is the total number of nodes in Q.

$$w_{q_i}=\frac{1}{t}{\displaystyle \sum _{j=1}^t(\frac{1}{r_j})}$$

(4)

The node that has the highest score is selected and queued in Q (lines 10–11). This process is continued until the best k features have been selected. Note that the most important features among the selected k features are at the top of Q, and the least important features are at the bottom of Q.

2.4. Data and Code Availability

All data and scripts for this work can be found at https://github.com/abu034004/SU-QMI.

3. Results

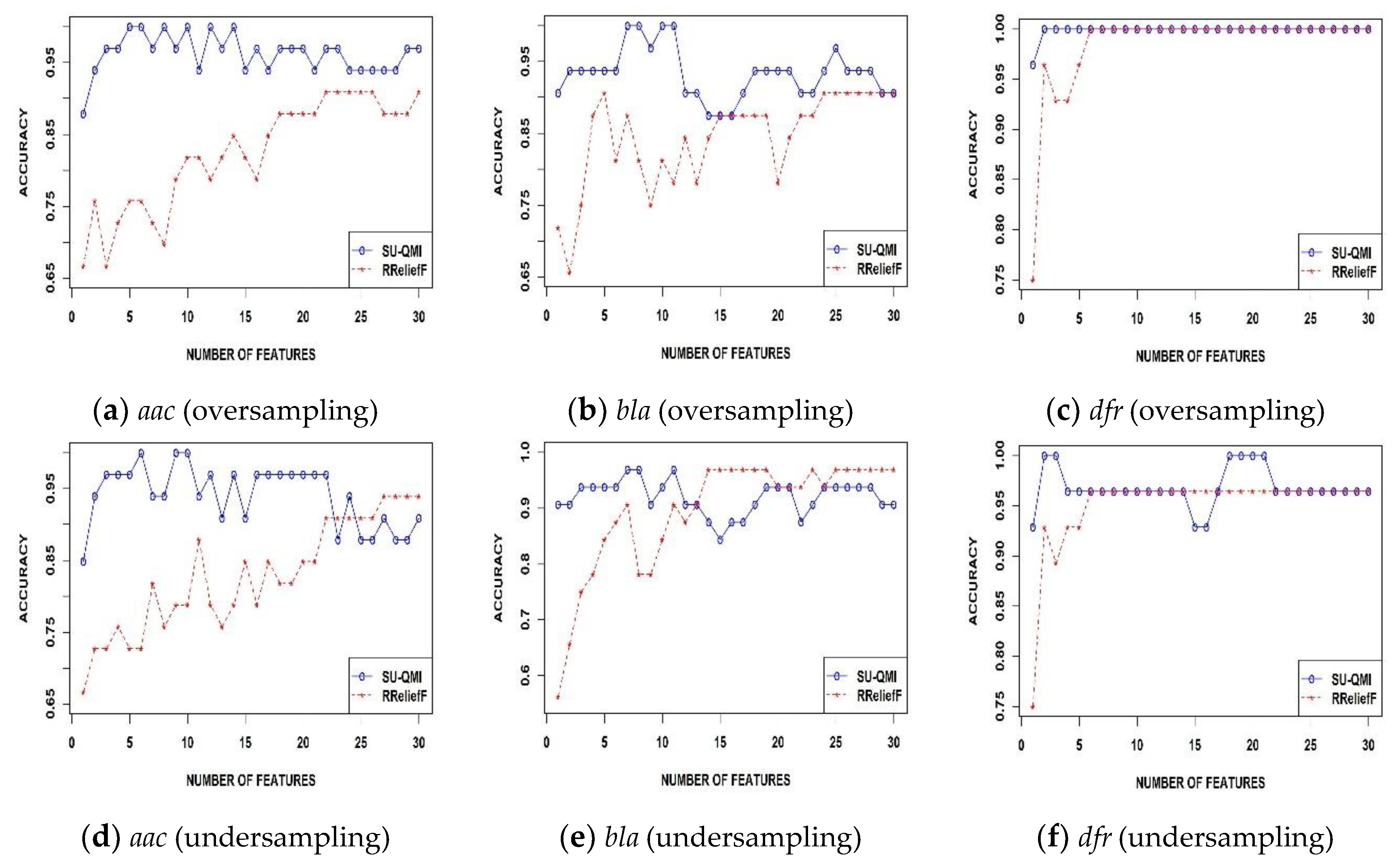
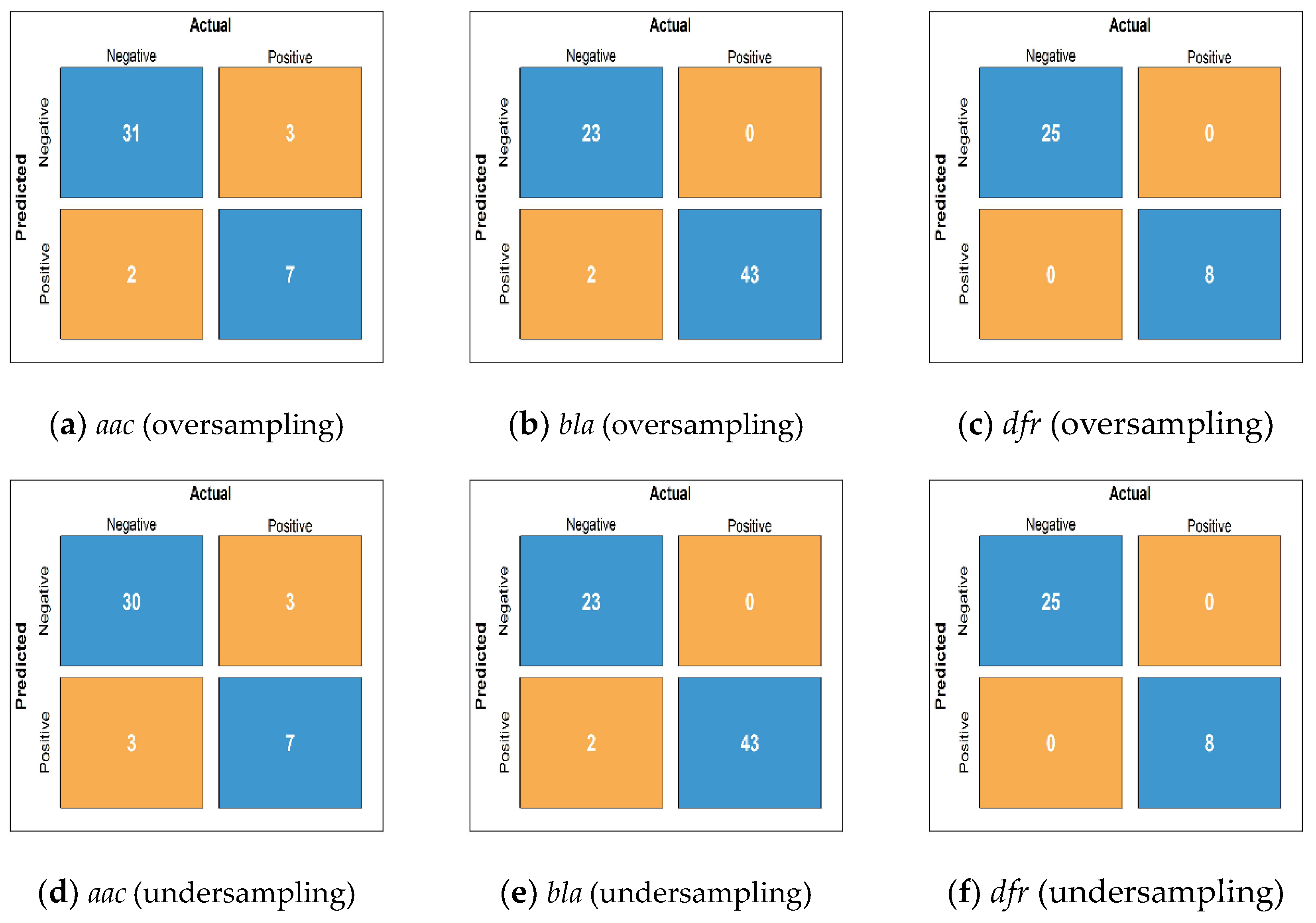
3.1. Comparative Analysis of the SU-QMI Feature Selection Method

We compare the performance of our SU-QMI approach with that of RReliefF. For RReliefF, we considered the same parameter settings (i.e., five neighbors and 30 instances), as suggested in [6]. Figure 1 shows results for the two approaches for both oversampling and undersampling. The performance of SU-QMI is generally better than that of RReliefF in terms of maximum accuracy w.r.t. the number of features. Although in two cases, RReliefF was able to achieve the same accuracies as the SU-QMI approach, the former required more features.

3.2. Identification of Antimicrobial-Resistance Proteins in Independent Datasets

To measure the predictive power of the SU-QMI method on unknown sequences, we trained an SVM model with all the sequences from the Gram-negative bacteria Acinetobacter, Klebsiella, Campylobacter, Salmonella, and Escherichia and then used the classifier to test sequences from three Gram-negative bacterial genera—Pseudomonas, Vibrio, and Enterobacter. The results are shown as confusion matrices in Figure 2. We obtained accuracies of 0.88, 0.97, and 1 for the three AMR classes, respectively, for the oversampling case, and it is worth noting that our method successfully classified all non-ARG samples of acetyltransferase as negative samples. For the undersampling case, accuracies of 0.86, 0.97, and 1 were obtained, but two of the eight non-ARG acetyltransferases were incorrectly predicted to be positive. Based on these results, our SU-QMI algorithm performs better with oversampling.

We also compared the SU-QMI algorithm with BLASTp (https://blast.ncbi.nlm.nih.gov/Blast.cgi?PAGE=Proteins) using default parameter settings. The performance of both approaches was comparable for aac and dfr with a percent identity ≥90 for BLASTp; however, in order to identify the same number of true positives as SU-QMI using oversampling for bla (Figure 2), the percent identity for BLASTp was 53%, and this threshold produced six false positives. Therefore, when classifying bla sequences, the false positive rate was higher for BLASTp than for SU-QMI.

4. Discussion

In this paper we presented a feature selection method SU-QMI based on SU, QMI, and graph theory to select an effective feature subset to use with a machine learning model to predict ARGs in Gram-negative bacteria. From the results, our SU-QMI algorithm is able to identify the most important features. We believe this is because feature selection is based not only on relevance and redundancy estimates, but also on interdependency among features. Our algorithm results in accuracies between 88 and 100% for three AMR classes and shows overall better performance than the RReliefF and BLASTp methods.