Proposal of Golf Swing Analysis Method Using Singular Value Decomposition †
Abstract
1. Introduction
2. Experiment to Measure Golf Swings
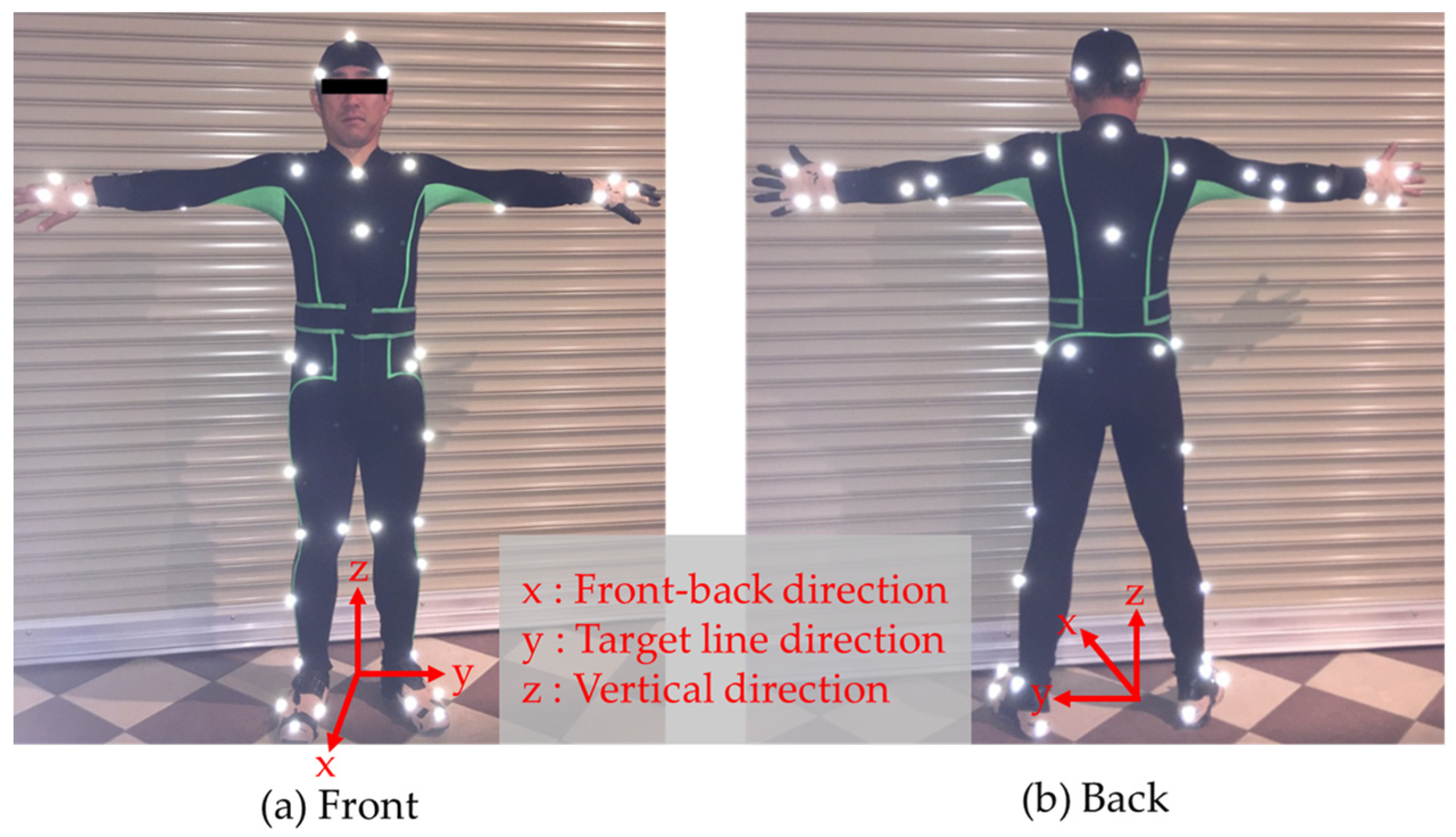
2.1. Preparations
2.2. Experiment Method
3. Motion Data Analysis
4. Analysis Using Singular Value Decomposition (SVD)
4.1. Construction of Observation Matrix
4.2. Singular Value Decomposition (SVD)
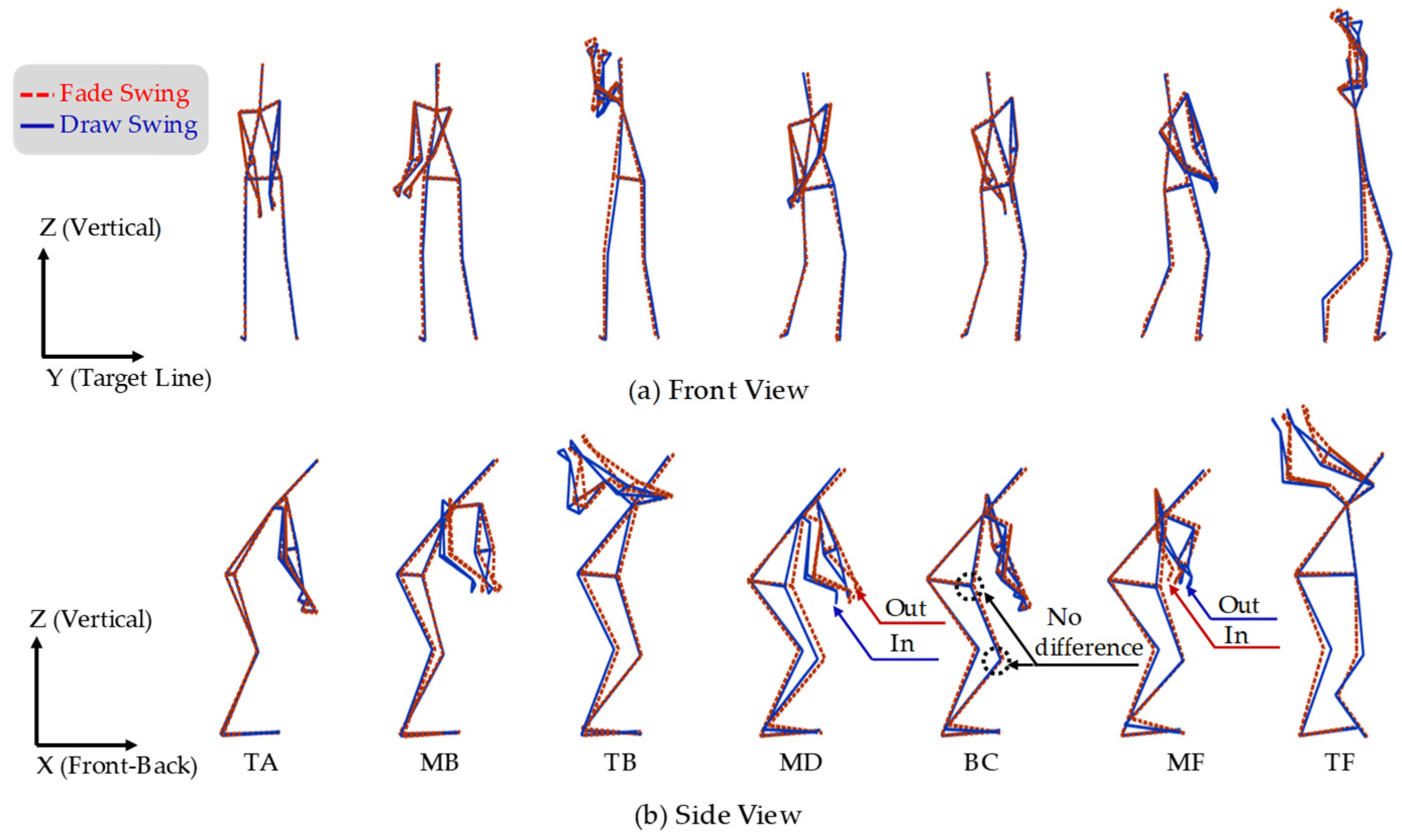
4.3. Analysis of Swing Behavior Reconstructed from Modes
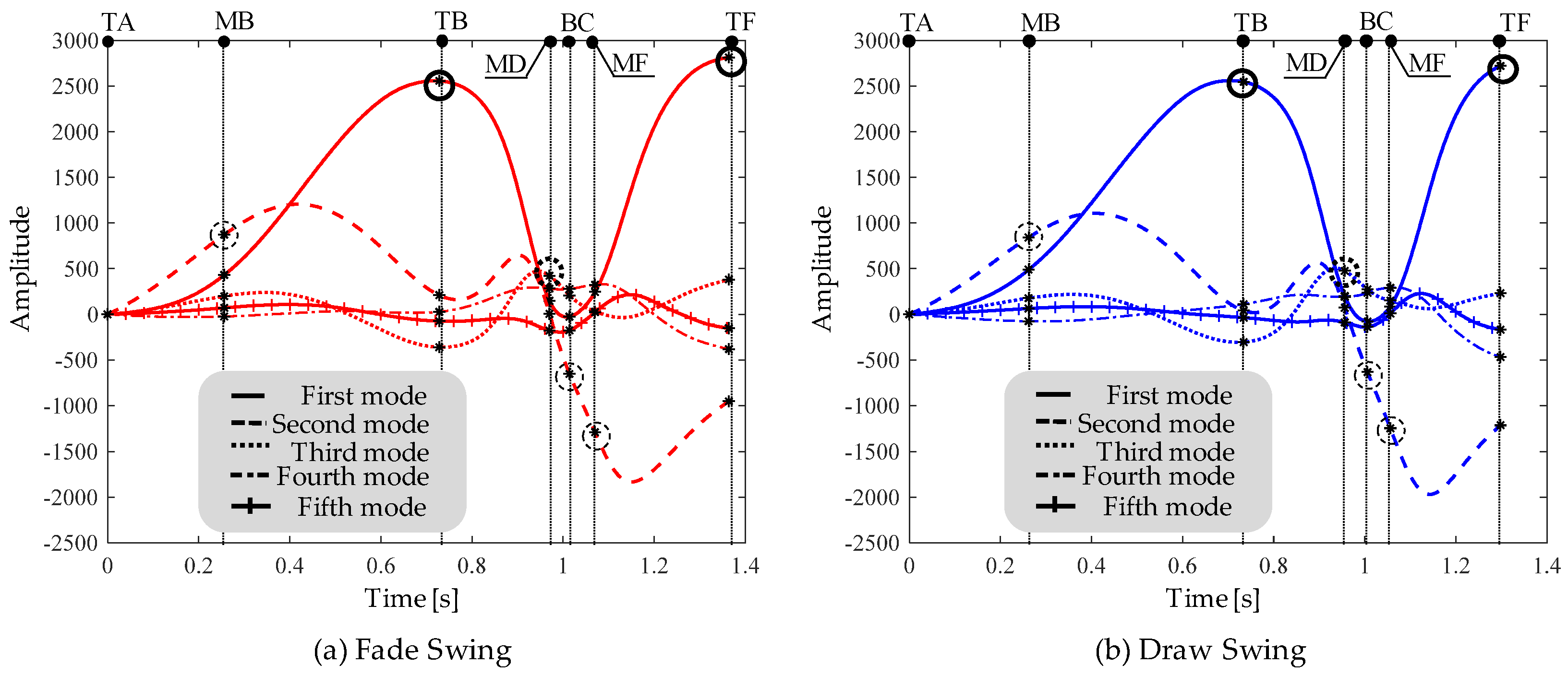
4.4. Comparison of Temporal Behaviors
5. Conclusions
- (1)
- Golf swings can now be analyzed in terms of independent modes which are in each role.
- (2)
- The SVD method can divide the analysis into dominant and accompanying motions.
Author Contributions
Funding
Conflicts of Interest
References
- Betzler, N.F.; Monk, S.A.; Wallace, E.; Otto, S.R. Effects of golf shaft stiffness on strain, clubhead presentation and wrist kinematics. Sports Biomech. 2012, 11, 223–238. [Google Scholar] [CrossRef]
- MacKenzie, S.J.; Sprigings, E.J. Understanding the mechanisms of shaft deflection in the golf swing. Sports Eng. 2009, 12, 69–75. [Google Scholar] [CrossRef]
- Matsumoto, K.; Tsujiuchi, N.; Koizumi, T.; Ito, A.; Ueda, M.; Okazaki, K. The Influence of a Golf Club’s Inertia on Shaft Movement during the Golfer’s Swing. Procedia Eng. 2016, 147, 360–365. [Google Scholar] [CrossRef][Green Version]
- MacKenzie, S.J. Club position relative to the golfer’s swing plane meaningfully affects swing dynamics. Sports Biomech. 2012, 11, 149–164. [Google Scholar] [CrossRef]
- Nesbit, S.M. A Three Dimentional Kinematic and Kinetic Study of the Golf Swing. J. Sports Sci. Med. 2005, 4, 499–519. [Google Scholar] [PubMed]
- Shimono, S.; Kodama, H.; Suzki, K. Optimal design for golf club considering swing motion adjustments by the shaft variations. Trans. JSME 2016, 82, 1–11. (In Japanese) [Google Scholar]
- Ivanenko, Y.; Cappellini, G.; Dominici, N.; Poppele, R.E.; Lacquaniti, F. Modular Control of Limb Movements during Human Locomotion. J. Neurosci. 2007, 27, 11149–11161. [Google Scholar] [CrossRef] [PubMed]
- Funato, T.; Aoi, S.; Oshima, H.; Tsuchiya, K. Variant and invariant patterns embedded in huma locomotion through whole body kinemtic coordination. Exp. Brain Res. 2010, 205, 497–511. [Google Scholar] [CrossRef] [PubMed]
- Shibata, K.; Harakawa, T.; Kawaguti, T. Dynamics and Motion Control of Golf Swing (1st Report)—A Study for Modelling to Reproduce Golf Swing. J. Jpn. Soc. Precis. Eng. 2002, 68, 397–402. [Google Scholar] [CrossRef]
- Matsumoto, K.; Tsujiuchi, N.; Ito, A.; Oshima, H.; Ueda, M.; Okazki, K. Motion Analysis of a Golf Swing using Singular Value Decomposition for Designing the Golf Club. J. Jpn. Soc. Des. Eng. 2018, 53, 447–462. [Google Scholar]
- Matsumoto, K.; Tsujiuchi, N.; Ito, A.; Kobayshi, H.; Ueda, M.; Okazaki, K. Analysis of Cooperative Action generating Trajectory in a Golf Swing. In Proceedings of the Symposium on Sports and Human Dynamics 2019, Fukuoka, Japan, 27 October 2019. [Google Scholar]
- Healy, A.; Moran, K.A.; Dickson, J.; Hurley, C.; Smeaton, A.F.; O’Connor, N.E.; Kelly, P.; Haahr, M.; Chockalingam, N. Analysis of the 5 Iron Golf Swing when Hitting for Maximum Distance. J. Sports Sci. 2011, 29, 1079–1088. [Google Scholar] [CrossRef] [PubMed]


| Height [cm] | Weight [kg] | Average Score |
|---|---|---|
| 171 | 70 | 75 |
| Action | |
|---|---|
| First mode | Steady rotation of legs, waist and rotation of arms in a swing as a whole |
| Second mode | Rotation of shoulders in a swing as a whole |
| Third mode | Extrusion and rotation of legs and waist from TB to TF |
| Forth mode | Rotation of shoulders and arms around BC |
| Fifth mode | Extension of arms from BC to TF |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matsumoto, K.; Tsujiuchi, N.; Ito, A.; Kobayashi, H.; Ueda, M.; Okazaki, K. Proposal of Golf Swing Analysis Method Using Singular Value Decomposition. Proceedings 2020, 49, 91. https://doi.org/10.3390/proceedings2020049091
Matsumoto K, Tsujiuchi N, Ito A, Kobayashi H, Ueda M, Okazaki K. Proposal of Golf Swing Analysis Method Using Singular Value Decomposition. Proceedings. 2020; 49(1):91. https://doi.org/10.3390/proceedings2020049091
Chicago/Turabian StyleMatsumoto, Kenta, Nobutaka Tsujiuchi, Akihito Ito, Hiroshi Kobayashi, Masahiko Ueda, and Kosuke Okazaki. 2020. "Proposal of Golf Swing Analysis Method Using Singular Value Decomposition" Proceedings 49, no. 1: 91. https://doi.org/10.3390/proceedings2020049091
APA StyleMatsumoto, K., Tsujiuchi, N., Ito, A., Kobayashi, H., Ueda, M., & Okazaki, K. (2020). Proposal of Golf Swing Analysis Method Using Singular Value Decomposition. Proceedings, 49(1), 91. https://doi.org/10.3390/proceedings2020049091




