Exploration of Center of Gravity, Moment of Inertia, and Launch Direction for Putters with Ball Speed Normalizing Face Properties ^†

Abstract

The forgiveness of golf putters is traditionally achieved through weight distribution. Putters are often designed with large footprints, which help to increase the moment of inertia (MOI), but consequently move the center of gravity (CG) farther behind the face. The use of higher MOI putters will result in less ball speed loss on impacts away from the sweet spot (i.e., more forgiveness). It has been shown that certain face properties, such as milling patterns, grooves, or soft inserts, can be leveraged to have a similar effect. This paper explores the relationships between impact location, MOI, CG depth, discretionary mass placement, and launch direction for these putters. A novel design strategy is proposed. Minimizing CG depth for putters with ball speed normalizing face properties, even at the expense of MOI, can result in more consistent launch direction and distance control for the average player.

1. Introduction

Putting accounts for more shots taken during a round of golf than any other type of shot [1]. One of the primary difficulties faced by amateur golfers is swing variability. In particular, amateurs tend to impact the putter face over a relatively large area, increasing the need for performance on poor strikes. For a golfer of handicap 18 and greater, this impact zone approximately resembles an oval with a width of 1.5 in and a height of 0.75 in [2]. These mishits lead to errors in both speed and direction [3,4].

The primary metric for forgiveness in golf clubs is moment of inertia (MOI). MOI is a measure of an object’s resistance to angular acceleration (rotation) around an axis for a given torque. It is a function of an object’s mass distribution relative to the axis of rotation. Most modern putters use perimeter weighting to increase MOI around the vertical axis [5]. Mass is often concentrated towards the heel and toe or rearward relative to the face. A golf club with large MOI will twist less when presented with a torque due to an off-center strike [4]. As a result, energy is transferred more efficiently to the ball, decreasing the penalty for a poor swing.

It has also been shown that the material properties of the clubhead can have a small influence on the energy transfer to the golf ball [2,6]. Putters with polymer inserts or deep grooves on the face, for example, perform slightly differently to those with a flat metal face. Efforts have been made by manufacturers to exploit this to improve ball speed consistency, with varying success. Other approaches to normalize ball speed have been considered as well, including a flexible impact surface [7] and a variable milling pattern [8].

With the increasing popularity of putters with ball speed normalizing face properties, it becomes prudent to reevaluate design strategy with respect to MOI and center of gravity (CG). A good putt must start the ball rolling on the target line and at the proper speed [1]. If a mishit putt can launch at the proper speed, greater emphasis can be put on the ball starting on the target line. This paper explores the relationships between MOI, CG, and launch direction, while assuming ball speed is constant over some region of the putter face.

2. Materials and Methods

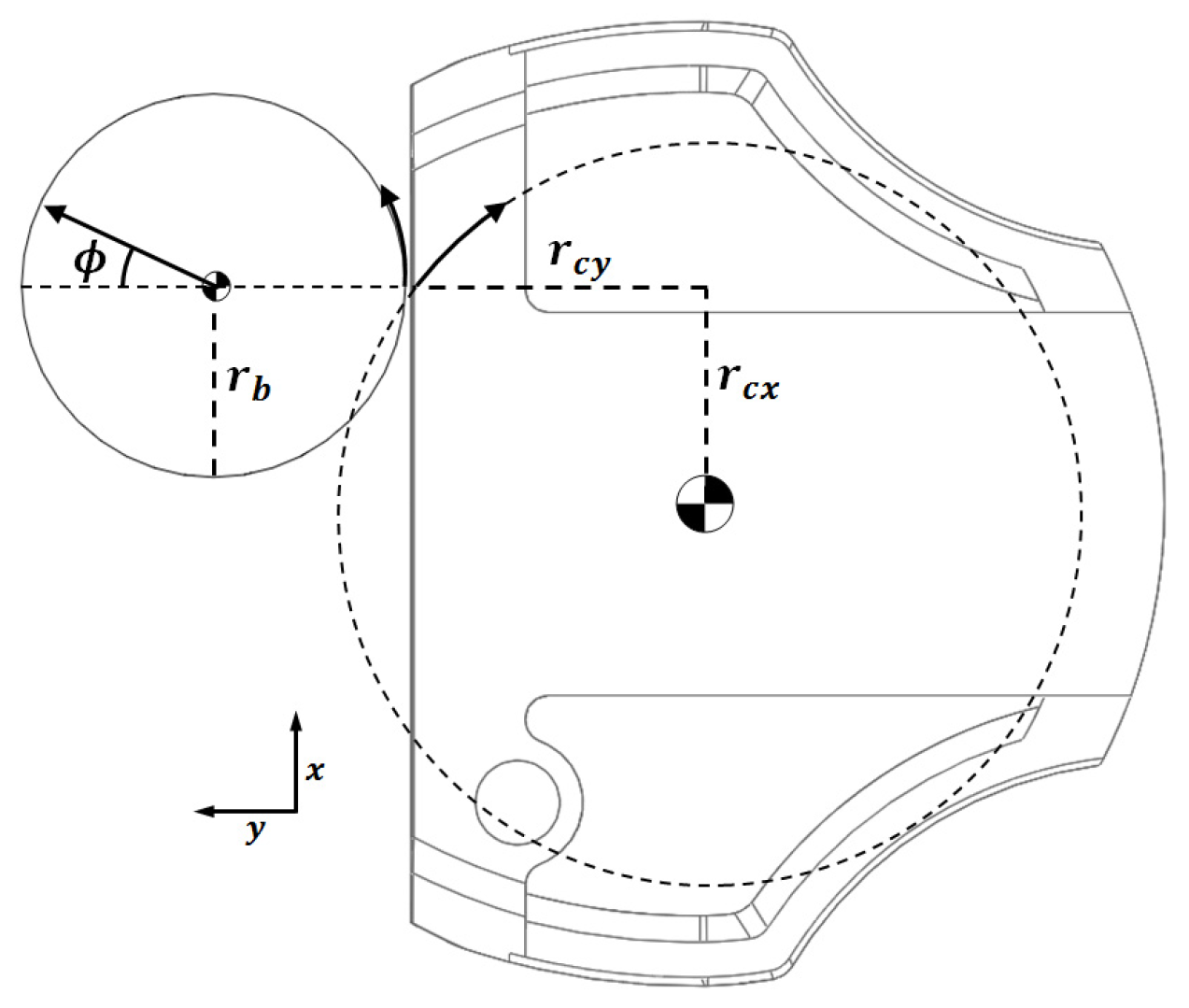
2.1. Impact Model

Due to the large forces and short duration of impact, a golf clubhead behaves largely like a free body, and the shaft has little effect [3,4]. The tendency for the clubhead to behave like a free body becomes very important for collisions away from the sweet spot, where a torque is introduced on the clubhead. The clubhead’s resulting rotation around its CG, if offset from the plane of the face, leads to a tangential velocity component at the impact location. The consequential frictional force on the ball leads to changes in spin and launch angle/direction; this is commonly referred to as gear effect. Various impact models have been developed that include this effect [9,10]. Figure 1 shows the gear effect for a deep CG mallet putter, along with some associated variables and notation.

Although widely treated as insignificant, the shaft has been shown to suppress the gear effect [5,11,12]. In addition, the forces on the clubhead are much smaller on a putt than a driver. Nonetheless, the CG depth of a putter will influence the ball’s spin [5] and launch direction [9] on a mishit.

For this paper, we will consider a free rigid body eccentric impact model with no slippage between the ball and clubface, developed by Penner [10]. For simplification, we will only consider normal impacts. That is, there is no loft at impact, and the face is square to the target line. With these assumptions, the launch direction of the ball simplifies to:

$$\varphi ={\tan }^{-1}\frac{I_b{m}_c{m}_b{r}_{cx}{r}_{cy}}{I_{cz}{m}_c{m}_b{r}_b^2+I_b{m}_c{m}_b{r}_{cy}^2+I_b{I}_{cz}{m}_c+I_b{I}_{cz}{m}_b},$$

where $I_b$ is the centroidal MOI of a golf ball, $m_c$ is the mass of the clubhead, $m_b$ is the mass of a golf ball, $r_b$ is the radius of the golf ball, $r_{cx}$ is the distance from the club CG to the impact location in the heel-toe direction, $r_{cy}$ is the CG depth, and $I_{cz}$ is the centroidal MOI of the clubhead around the vertical axis (i.e., heel-toe MOI). It is interesting to note that the launch direction becomes independent of the coefficient of restitution (COR) and clubhead speed. Also, because we are dealing with small angles, $\varphi \propto r_{cx}$. For this analysis, we assume that the mass of the clubhead is a constant 360 g, and the ball is a uniformly dense solid sphere with mass of 46 g, radius of 21.35 mm, and MOI of $0.4 m_b{r}_b^2$. The launch direction is then:

$$\varphi ={\tan }^{-1}\frac{r_{cx}{r}_{cy}}{r_{cy}^2+0.079 I_{cz}} .$$

The launch direction is calculated for many potential values of clubhead heel-toe MOI ($I_{cz}$) and CG depth ($r_{cy}$). Figure 2 shows these relationships for a 15 mm toe impact ($r_{cx}=15 \mathrm{mm}$).

As expected, the launch direction shrinks with an increase in MOI or a decrease in CG depth. Based on this model and impact, the ball will launch 0.5° offline for both a 4000 g cm² putter with a CG depth of 18.5 mm and a 6000 g cm² putter with a CG depth of 28.0 mm. On a straight putt and standard sized golf hole (4.25” diameter), a putt launched at this angle relative to the center of the hole will intersect the edge of the hole at approximately 20 ft.

2.2. Discretionary Mass Placement

Designing a putter with minimal CG depth and/or maximum MOI is not complicated. Clubhead designers, however, are restricted based on the visual preferences of the target player. A larger, deeper shape, for example, is often preferred for alignment.

It is common for the required mass to achieve the desired shape to be less than the target mass of the clubhead. The result is a certain amount of extra discretionary mass that can be strategically placed to improve performance. Assuming ball speed is constant for any reasonable mishit, discretionary mass should be placed to minimize offline launch direction. From (2), the launch direction is a function of both the CG depth and MOI, but they are not easily isolated because moving mass in the clubhead affects both. Consider a clubhead with discretionary point masses placed symmetrically about the heel and toe. The new CG depth can be calculated as:

$$r_{cy}^{\text{'}}=\frac{m_c{r}_{cy}+m_p{r}_{py}}{m_c+m_p} ,$$

where $m_c$ is the initial clubhead mass, $r_{cy}$ is the normal distance from the face plane to the initial clubhead CG, $m_p$ is the total discretionary point mass, and $r_{py}$ is the normal distance from the face plane to the point mass. The new MOI of the clubhead is then:

$$I_{cz}^{\text{'}}=I_{cz}+m_c{\left(r_{cy}-r_{cy}^{\text{'}}\right)}^2+m_p\left(r_{px}^2+{\left(r_{py}-r_{cy}^{\text{'}}\right)}^2\right).$$

The effect of discretionary mass placement on launch direction, given an initial clubhead mass, CG, and MOI, can be determined from (2)–(4). A few scenarios are considered in Figure 3. For each plot, negative and positive values for $r_{px}$ are shown as a visual aid, but because heel-toe symmetry is assumed in (4), it is not necessary. Scenarios 1 and 2 have small discretionary mass and thus larger initial MOI. Scenarios 3 and 4 have large discretionary mass and thus smaller initial MOI. Scenarios 1 and 3 have a shallow initial CG similar to a blade or small mallet. Scenarios 2 and 4 have a deep initial CG similar to a large mallet.

It is clear from the charts above that discretionary mass should be placed as far towards the heel and toe as possible to minimize launch direction on a mishit. This is to be expected because increasing $r_{px}$ increases $I_{cz}^{\text{'}}$ but has no effect on $r_{cy}^{\text{'}}$. An interesting observation comes from the optimal value for $r_{py}$. For each scenario, increasing $r_{py}$ eventually becomes most effective for decreasing launch direction, but this occurs outside the usual footprint for putters. In most instances, it appears that launch direction is minimized when mass is placed towards the face and at the heel and toe. The exception in the above plots occurs in (b), where a small amount of mass is available and the original CG depth is somewhat large. If placed more than 100 mm behind the face, the launch direction becomes smaller than if placed at the face. Of course, this is only possible if the shape of the putter extends to this range. Due to the proportionality between $r_{cx}$ and $\varphi$, the optimal location for discretionary mass placement does not change based on impact location.

2.3. Physical Testing

A putter with adjustable weights was used to test the validity of the above model and assumptions. The putter has a mass of 360 g and allows for many different configurations to adjust CG location and MOI. Two configurations of this putter, shown in Figure 4, were tested. They represent mass concentrated towards the face and heel/toe versus mass concentrated away from the face and central. Configuration B has 20% larger heel-toe MOI than Configuration A, but it also has a much deeper CG location.

The putters were tested with a putter pendulum with magnetic release for consistent head delivery (head speed of 3.6 mph). A golf ball without dimples was used to remove any inconsistencies that may result from contacting the edge of a dimple differently from shot to shot. Ten putts were hit at face center, heel (−15 mm), and toe (+15 mm) for both putter configurations. A flat brushed mat allowed the ball to leave a trace which could then be accurately measured for launch direction.

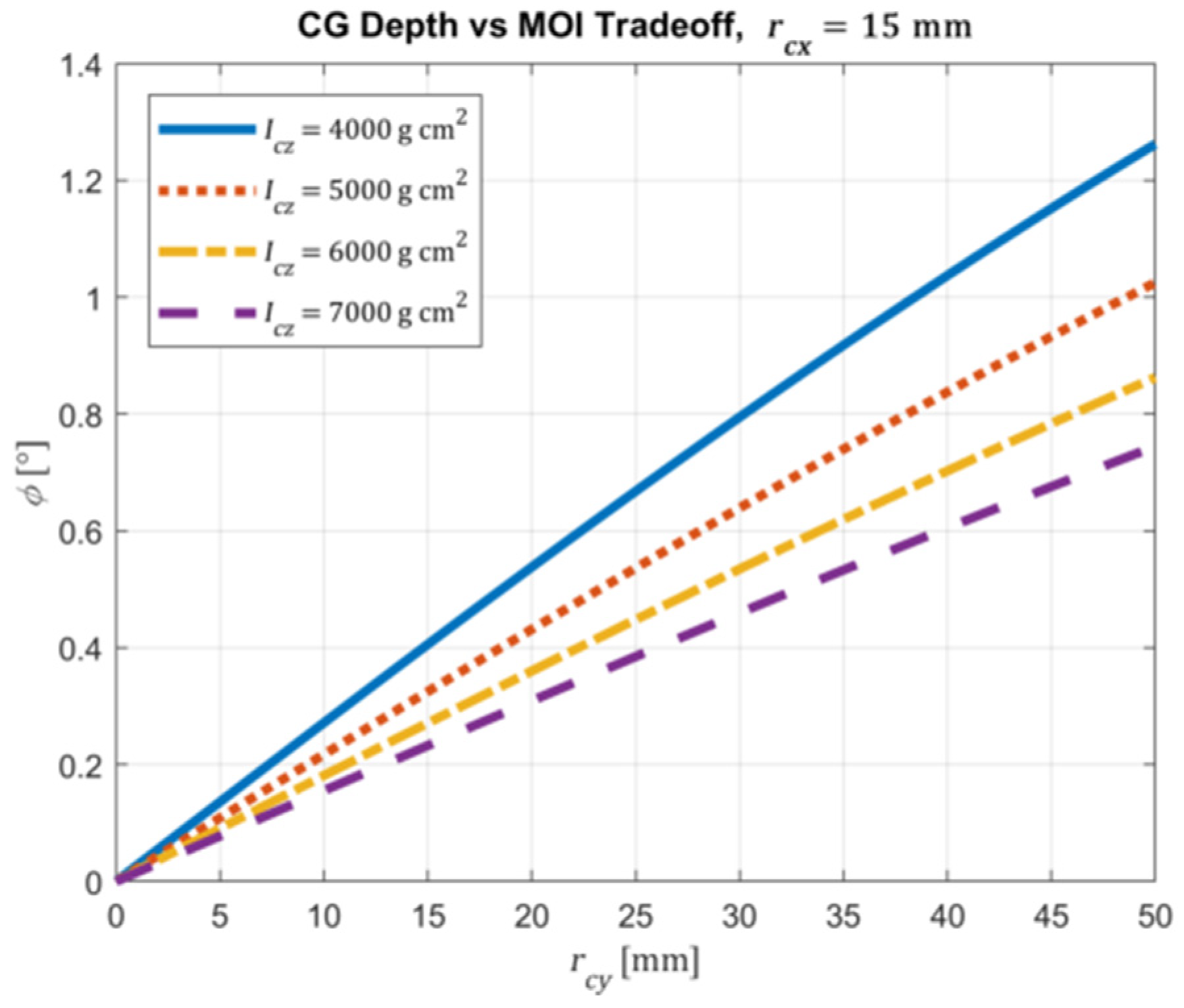
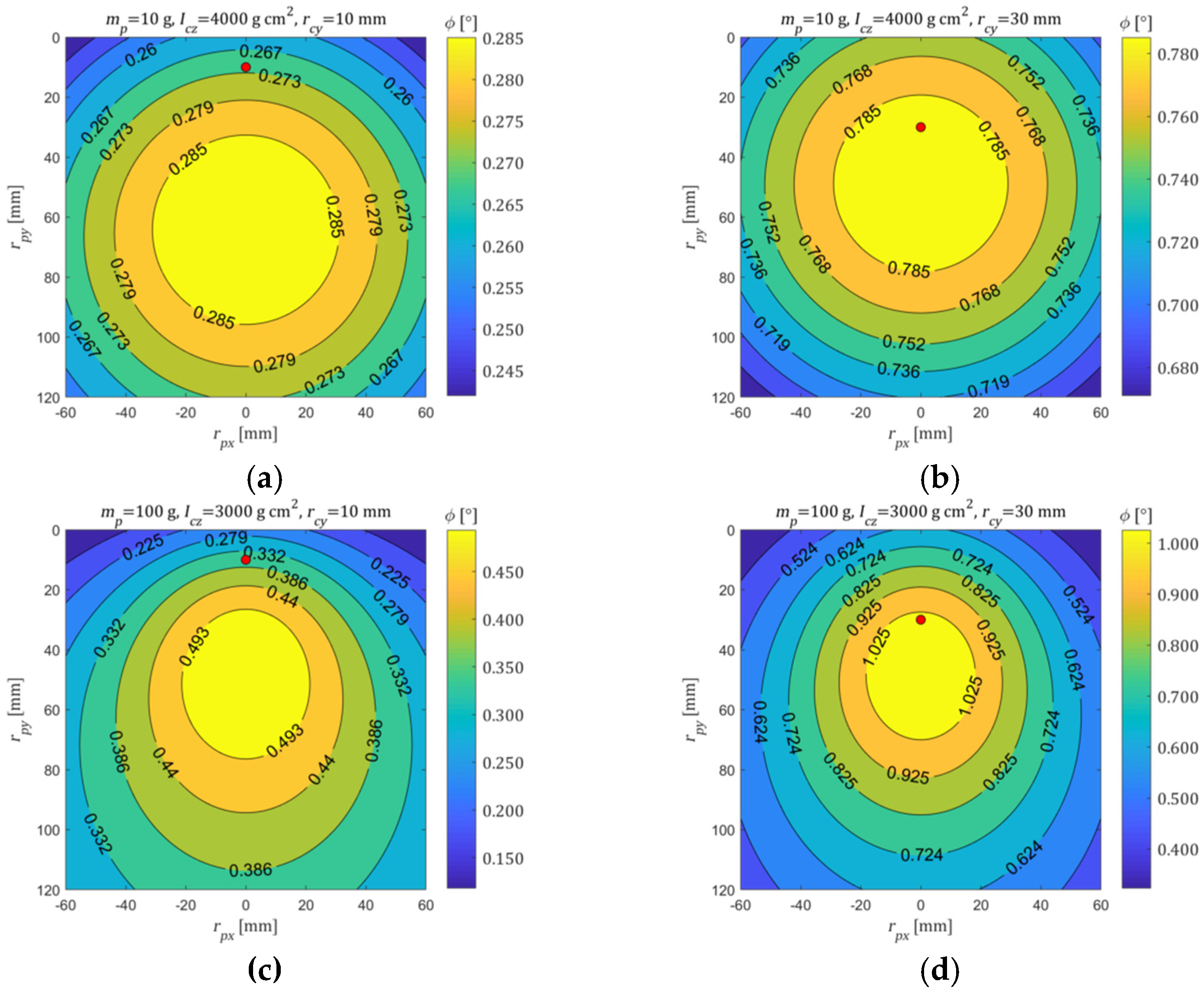
3. Results

The average launch direction ($\varphi$) for each impact location and putter configuration with the pendulum is shown in

Table 1. Test results of putter configuration 1 and putter configuration 2.

Putter	${\mathit{r}}_{\mathit{c}\mathit{x}}\left(\mathbf{Impact}\mathbf{Location}\right)$	$\mathbf{Test}\mathit{\varphi }$ ± 95% CI	$\mathbf{Simulated}\mathit{\varphi }$	Difference
Configuration A	−15 mm (Heel)	−0.58° ± 0.13°	−0.30°	−0.28°
	0 mm (Center)	0.00° ± 0.10°	0.00°	0.00°
	15 mm (Toe)	0.23° ± 0.18°	0.30°	−0.07°
Configuration B	−15 mm (Heel)	−0.72° ± 0.18°	−0.56°	−0.16°
	0 mm (Center)	0.00° ± 0.05°	0.00°	0.00°
	15 mm (Toe)	0.59° ± 0.10°	0.56°	0.03°

. The launch direction is normalized to the average value for center impacts for each putter and compared to the corresponding simulated launch direction from (2).

The test results agree fairly well with the simulated impacts, considering the small magnitudes of the data and the associated difficulties of accurate measurement. Heel impacts tend to pull the ball left, while toe impacts push the ball right. According to (2), Configuration B will have a greater gear effect than Configuration A, despite its larger MOI. This is due to its significantly deeper CG. The test results show the same trend, where heel and toe impacts lead to a greater off-line launch direction for Configuration B than Configuration A.

On average, the heel impacts for both putters tend to travel further off-line than expected, while the toe impacts more closely match the impact model. As the putter shaft is adhered at the heel of the clubhead, one would expect that any asymmetry in launch direction would be in the opposite direction of what this test shows. It is possible this is the result of inconsistencies in the test setup or measurement process, but it should be investigated further. In addition, certain predictions seen in the model are not tested, including proportionality between impact location and launch direction as well as independence between launch direction and impact speed. To more accurately quantify the benefits of a shallow CG design, a more thorough validation of the model should be done.

4. Discussion

It is apparent from physical testing that the gear effect can be significant and follows the trends predicted from the rigid free body impact model. Based on the physical testing, a 15 mm impact towards the toe launched 0.23° offline for a shallow CG putter and 0.59° offline for a deep CG putter, even though the deep CG putter had 20% larger heel-toe MOI. Putts that start 0.23° and 0.59° offline will travel outside the radius of the hole at 47 and 18 ft, respectively. Although reading the green correctly and delivering the clubhead as intended are certainly the most important parts of putting well, the resulting directional error due to a mis-hit is significant. In addition, the impact scenario under consideration (15 mm away from the sweet spot) is inside the horizontal impact error seen for many amateur golfers [2].

For the purpose of this paper, it is assumed that ball speed is constant relative to the impact location. However, there are limits to ball speed normalization via progressive face properties. This generally appears to be around 20 mm horizontally from the sweet spot, depending on the MOI of the specific putter [7,8]. In addition, progressive face properties may be limited or avoided altogether based on feel preferences. In these instances, the relationships between impact location, ball speed, and launch direction must all be considered.

To better quantify the benefits of this design approach, a strokes gained metric [13] may be used in future analysis. For any subset of golfers, one may consider their impact distribution, head delivery variability, and green reading tendencies, ultimately predicting a net difference in strokes per round or shot. This, of course, is much more complicated than predicting launch conditions from a putter pendulum. Nonetheless, one can conclude from this analysis that many amateur golfers may benefit from a shallow-CG design, especially when ball speed is normalized.

5. Conclusions

Due to the increasing popularity of putters with ball speed normalizing face properties, putter design was explored with a focus on launch direction. A rigid body impact model was used to determine the relationships between impact location, CG depth, heel-toe MOI, and launch direction. A hypothetical scenario was considered where a putter with initial mass, CG depth, and MOI has a certain amount of discretionary mass available for placement. Under the scenarios considered, the preferred placement of the discretionary mass to minimize launch direction on a mishit was close to the face and towards the heel and toe.

A physical test was conducted with an adjustable CG/MOI putter set to two different configurations. Launch direction was recorded for impacts at heel, center, and toe. The heel and toe impacts represented realistic mishits for an amateur golfer. It was found that the gear effect predicted via the impact model was present, and the higher MOI putter with deeper CG launched more offline for the heel and toe impacts. Further investigation and testing should be performed to more accurately model the gear effect in putters. Nonetheless, putters with ball speed normalizing face properties should be designed with greater emphasis on decreasing CG depth rather than increasing MOI to improve overall performance.