Shoe–Surface Tribology in Hardcourt Tennis †
Abstract
1. Introduction
2. Materials and Methods
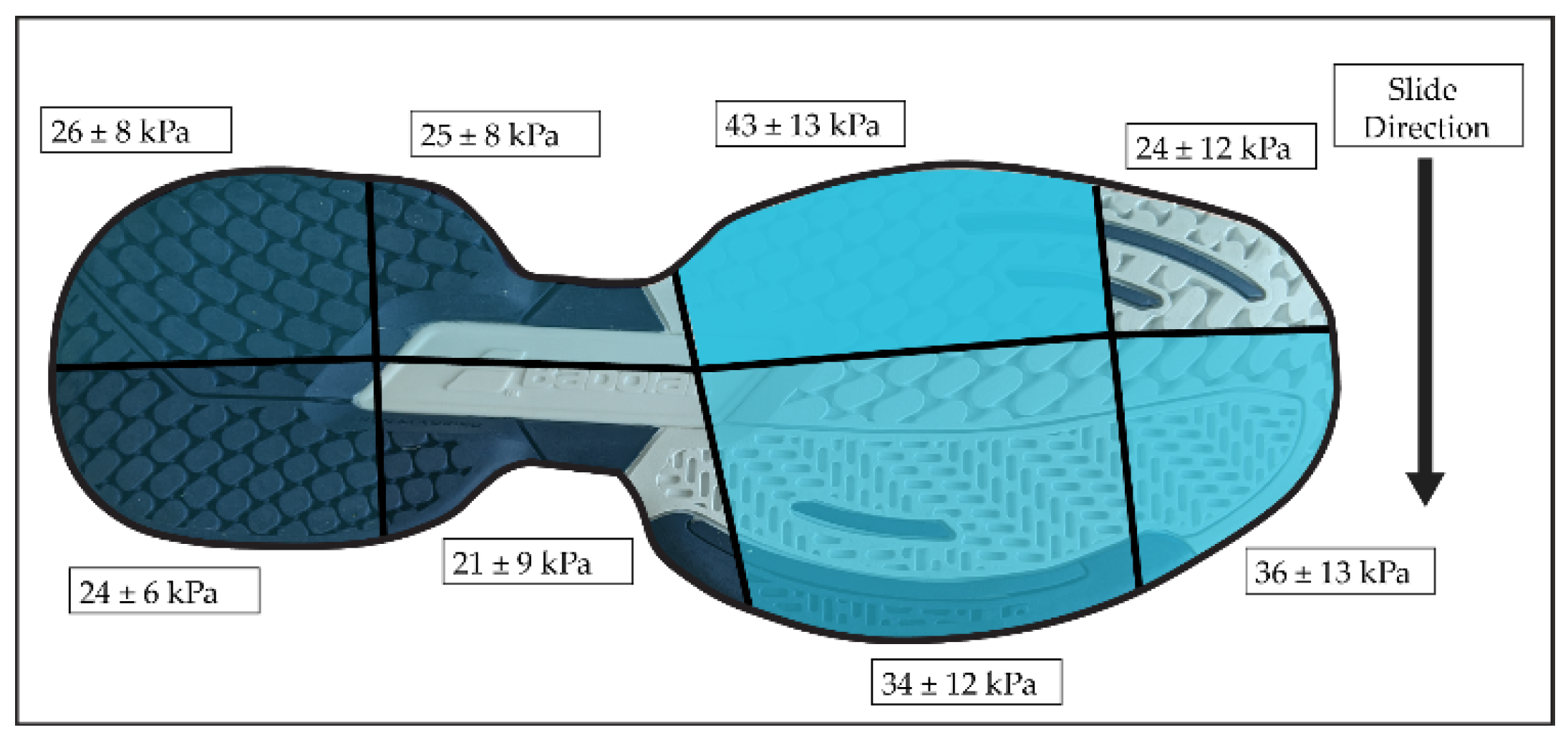
2.1. Tread Elements and Hardcourt Surface
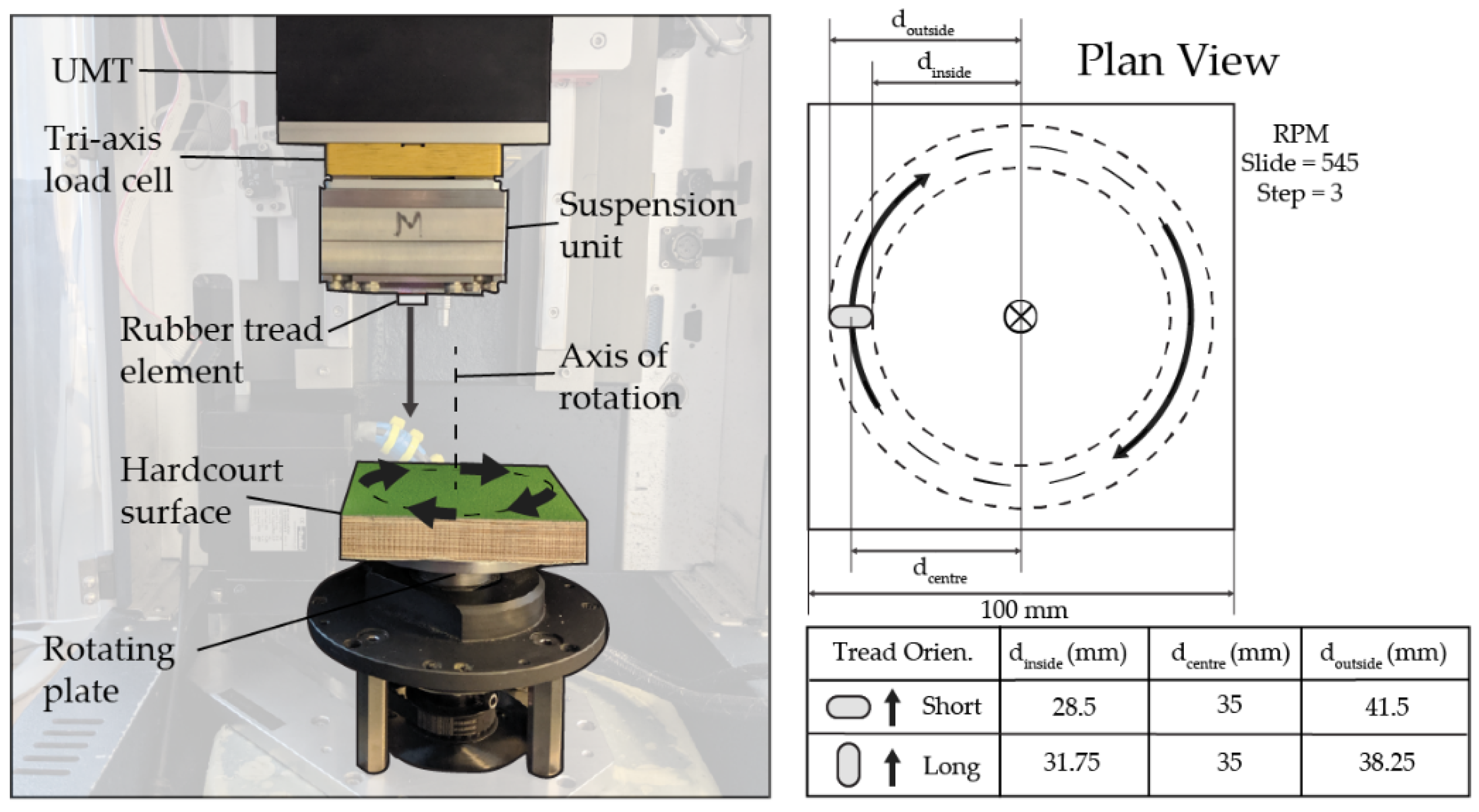
2.2. Experimental Set-Up
2.3. Experiment Summary
3. Results
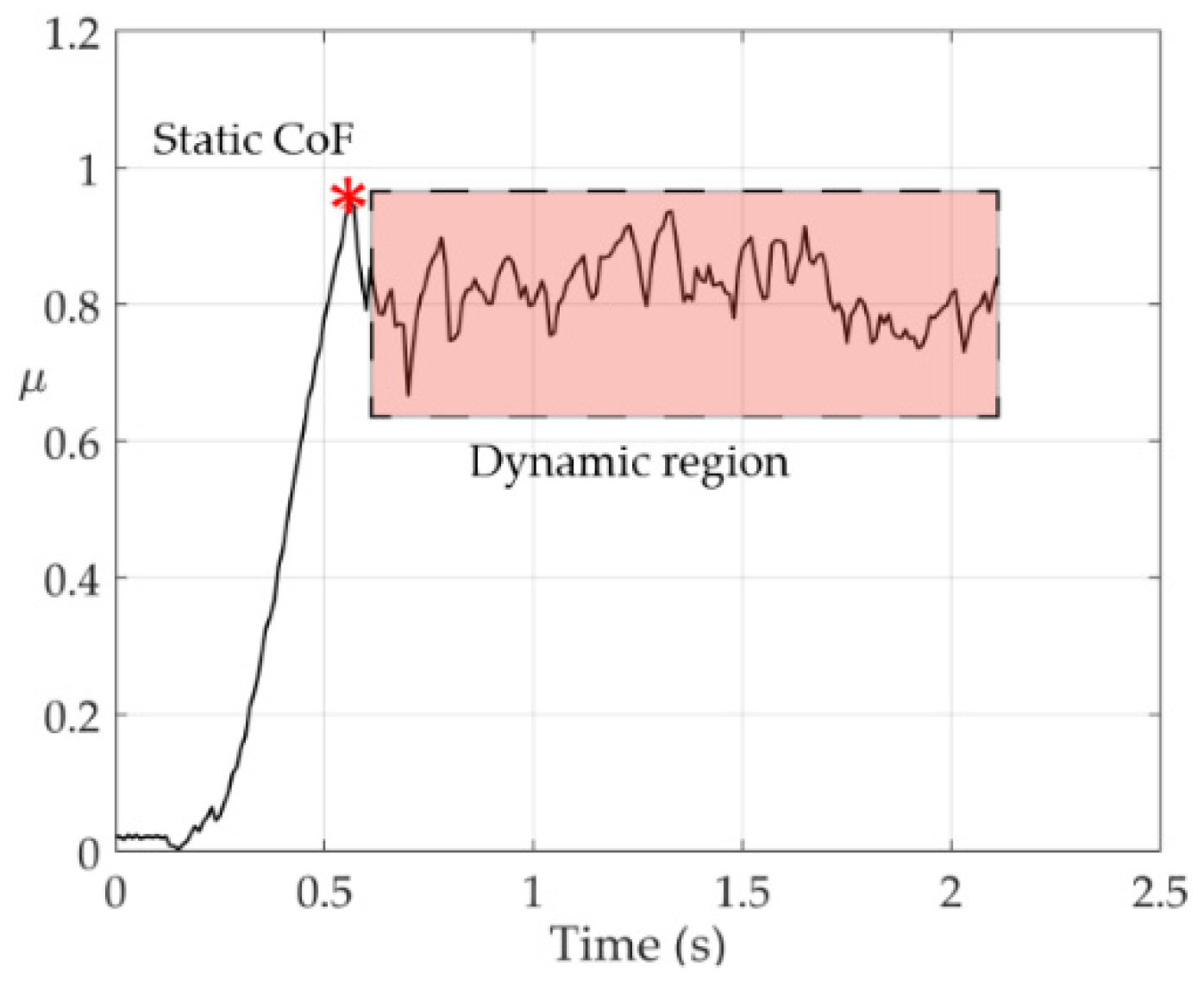
3.1. Step Movement Coefficient of Friction
3.2. Slide Movement Coefficient of Friction
3.3. Tread Orientation
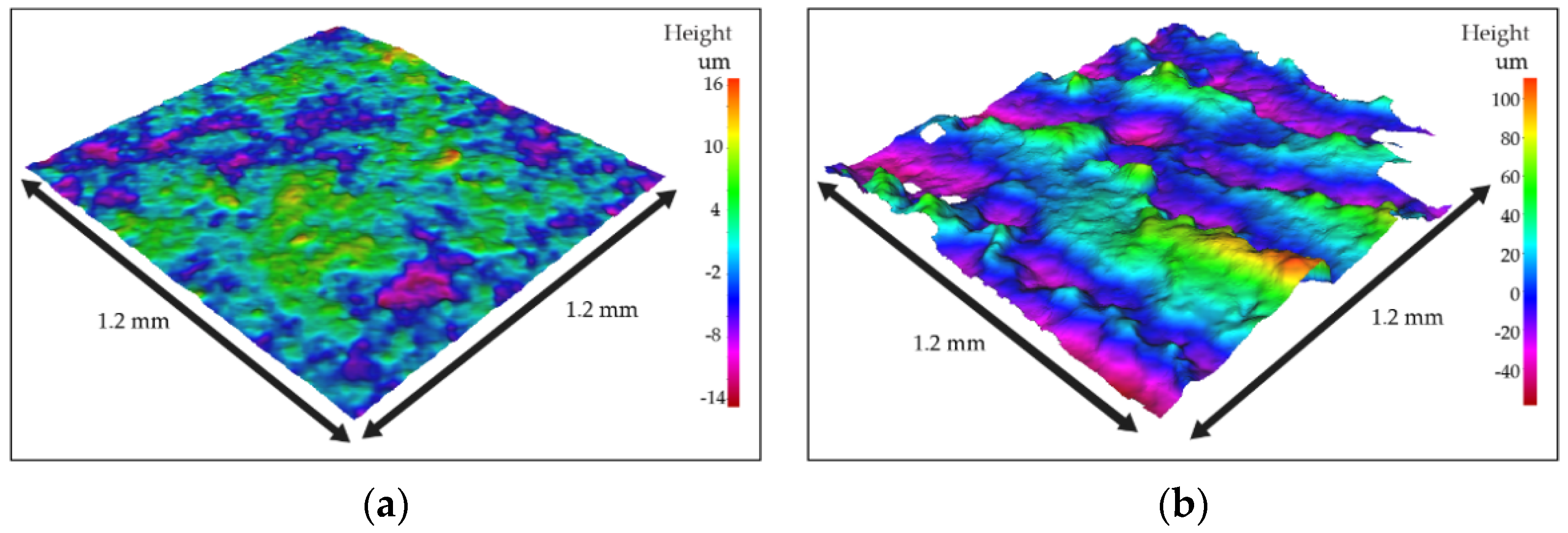
3.4. Wear Analysis
4. Discussion
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Nigg, B.M.; Stefanyshyn, D.J.; Rozitis, A.I.; Mündermann, A. Resultant knee joint moments for lateral movement tasks on sliding and non-sliding sport surfaces. J. Sports Sci. 2009, 27, 427–435. [Google Scholar] [CrossRef] [PubMed]
- Luo, G.; Stefanyshyn, D. Identification of critical traction values for maximum athletic performance. Footwear Sci. 2011, 3, 127–138. [Google Scholar] [CrossRef]
- Worobets, J.; Wannop, J.W. Influence of basketball shoe mass, outsole traction, and forefoot bending stiffness on three athletic movements. Sport Biomech. 2015, 14, 351–360. [Google Scholar] [CrossRef] [PubMed]
- Goff, J.E.; Ura, D.; Boswell, L.; Carré, M.J. Parametric Study of Simulated Tennis Shoe Treads. Procedia Eng. 2016, 147, 443–448. [Google Scholar] [CrossRef]
- Goff, J.E.; Boswell, L.; Ura, D.; Kozy, M.; Carré, M. Critical shoe contact area ratio for sliding on a tennis hard court. Proc. Inst. Mech. Eng. Part P J. Sport Eng. Technol. 2018, 2, 112–121. [Google Scholar] [CrossRef]
- Ura, D.; Clarke, J.; Carré, M. Effect of shoe orientation on shoe-surface traction in tennis. Footwear Sci. 2013, 5, 86–87. [Google Scholar] [CrossRef][Green Version]
- Hale, J.; Lewis, R.; Carré, M.J. Rubber friction and the effect of shape. Tribol. Int. 2020, 141, 1–6. [Google Scholar] [CrossRef]
- Starbuck, C.; Damm, L.; Clarke, J.; Carré, M.; Capel-Davis, J.; Miller, S.; Stiles, V.; Dixon, S. The influence of tennis court surfaces on player perceptions and biomechanical response. J. Sports Sci. 2016, 34, 1627–1636. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Clarke, J.; Carré, M.J.; Damm, L.; Dixon, S. The development of an apparatus to understand the traction developed at the shoe-surface interface in tennis. Proc. Inst. Mech. Eng. Part P J. Sport Eng. Technol. 2013, 227, 149–160. [Google Scholar] [CrossRef]
- Emami, A.; Khaleghian, S. Investigation of tribological behavior of Styrene-Butadiene Rubber compound on asphalt-like surfaces. Tribol. Int. 2019, 136, 487–495. [Google Scholar] [CrossRef]
- Fortunato, G.; Ciaravola, V.; Furno, A.; Lorenz, B.; Persson, B.N.J. General theory of frictional heating with application to rubber friction. J. Phys. Condens. Matter. 2015, 27, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Needham, J.A.; Sharp, J.S. Watch your step! A frustrated total internal reflection approach to forensic footwear imaging. Sci. Rep. 2016, 6, 1–7. [Google Scholar] [CrossRef]
- Ura, D. Development of a Test Device to Measure the Tribological Behaviour of Shoe-Surface Interactions in Tennis. Ph.D. Thesis, University of Sheffield, Sheffield, UK, 2014. [Google Scholar]



| Movement | Test Parameters | ||
|---|---|---|---|
| Normal Load (N) | Slide Velocity (mm/s) | Total Slide Time (s) | |
| Step | 33 | 10 | 10 |
| Slide | 25 | 2000 | 0.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hale, J.; Lewis, R.; Carré, M.J. Shoe–Surface Tribology in Hardcourt Tennis. Proceedings 2020, 49, 90. https://doi.org/10.3390/proceedings2020049090
Hale J, Lewis R, Carré MJ. Shoe–Surface Tribology in Hardcourt Tennis. Proceedings. 2020; 49(1):90. https://doi.org/10.3390/proceedings2020049090
Chicago/Turabian StyleHale, John, Roger Lewis, and Matt J. Carré. 2020. "Shoe–Surface Tribology in Hardcourt Tennis" Proceedings 49, no. 1: 90. https://doi.org/10.3390/proceedings2020049090
APA StyleHale, J., Lewis, R., & Carré, M. J. (2020). Shoe–Surface Tribology in Hardcourt Tennis. Proceedings, 49(1), 90. https://doi.org/10.3390/proceedings2020049090






