Measurement of Flight Dynamics of a Frisbee Using a Triaxial MEMS Gyroscope †
Abstract
1. Introduction
2. Materials and Methods
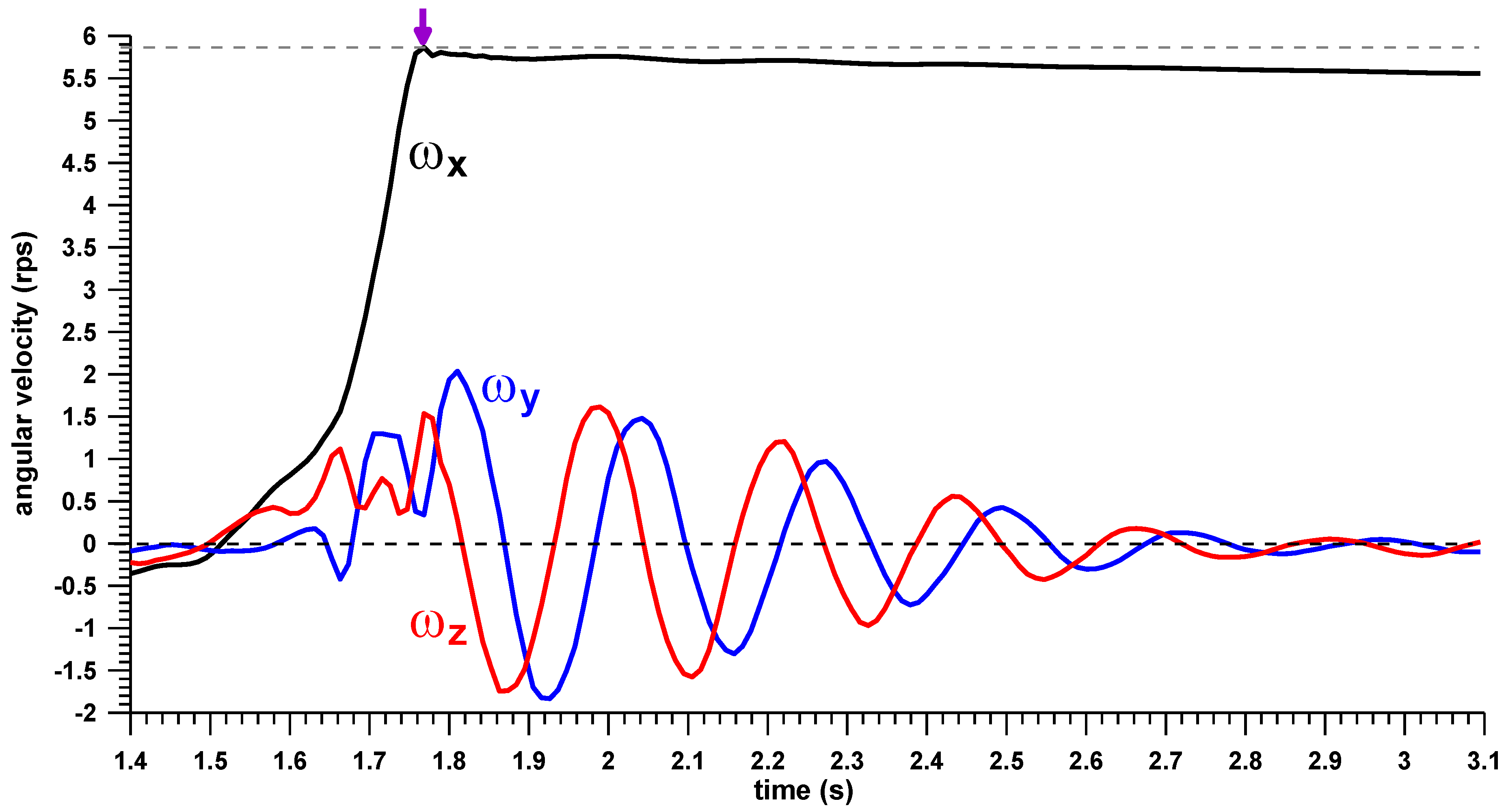
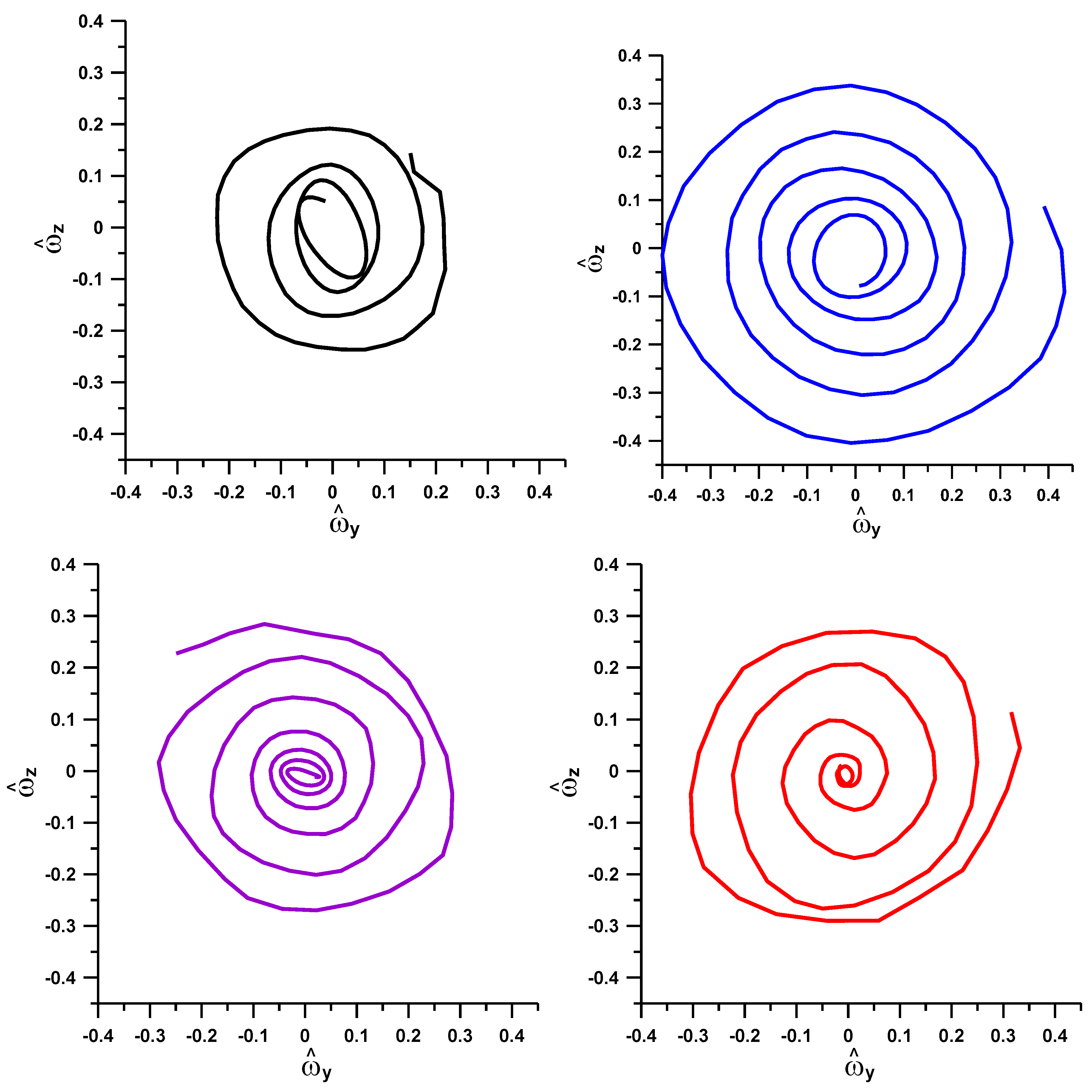
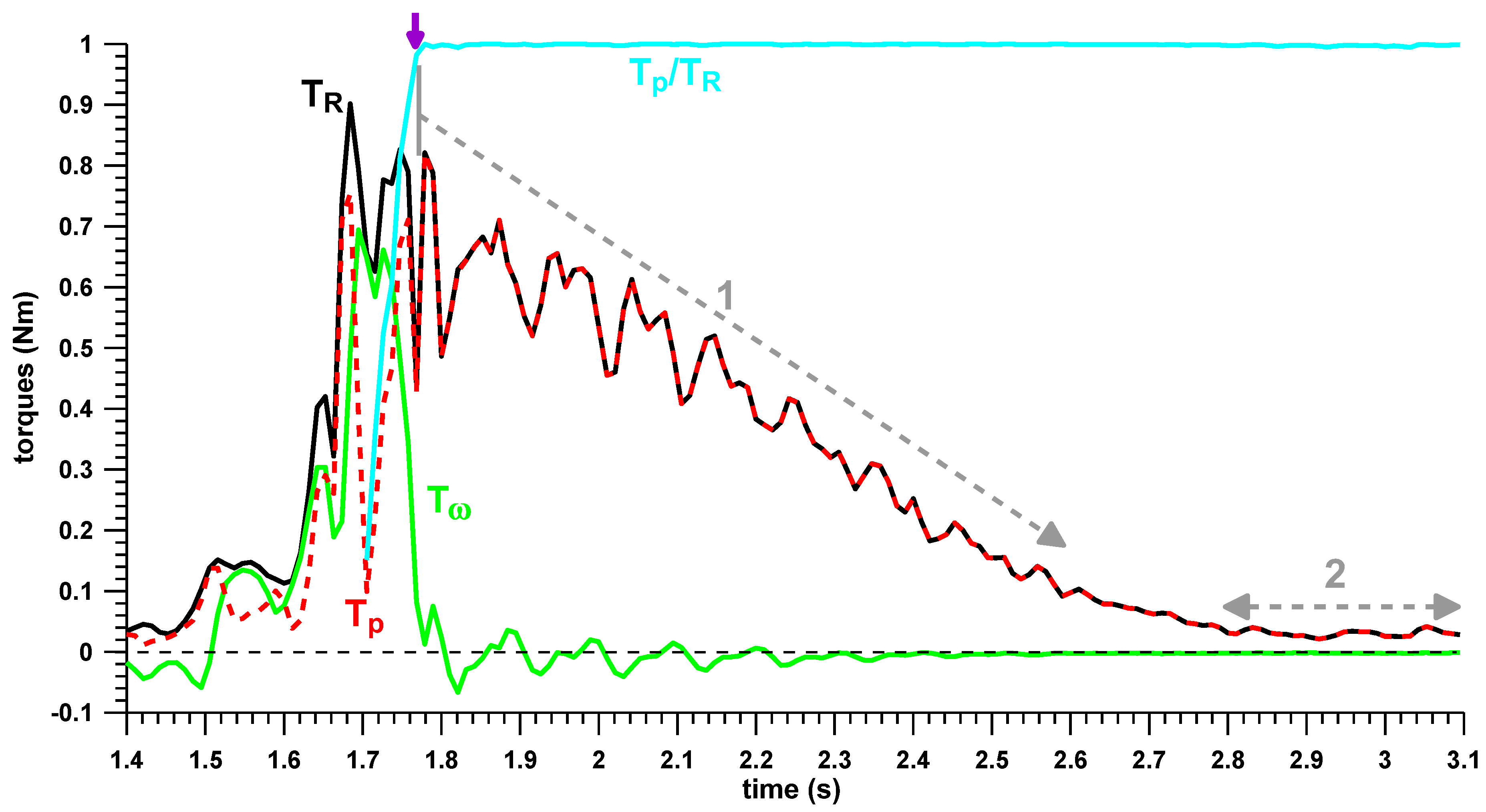
3. Results
4. Discussion
Funding
Conflicts of Interest
References
- Baumback, K. The Aerodynamics of Frisbee Flight. Undergrad. J. Math. Model. One Two 2010, 3. [Google Scholar] [CrossRef]
- Hubbard, M.; Hummel, S.A. Simulation of Frisbee flight. In Proceedings of the 5th Conference on Mathematics and Computers in Sport, University of Technology, Sydney, Australasia, 14–16 June 2000; pp. 124–134. [Google Scholar]
- Hummel, S.A. Frisbee Flight Simulation and Throw Biomechanics. Master’s Thesis, University of California, Davis, CA, USA, July 2003. [Google Scholar]
- Nakamura, Y.; Fukamachi, N. Visualization of the Flow Past a Frisbee. Fluid Dyn. Res. 1991, 7, 31–35. [Google Scholar] [CrossRef]
- Potts, J.R.; Crowther, W.J. Visualisation of the Flow Over a Disc-wing. In Proceedings of the Ninth International Symposium on Flow Visualization, Edinburgh, Scotland, UK, 22–25 August 2000. [Google Scholar]
- Koyanagi, R.; Seo, K.; Ohta, K.; Ohgi, Y. A Computer Simulation of the Flying Disc Based on the Wind Tunnel Test Data. Procedia Eng. 2012, 34, 80–85. [Google Scholar] [CrossRef][Green Version]
- Hummel, S.; Hubbard, M. Identification of Frisbee Aerodynamic Coefficients Using flight data. In Proceedings of the 4th International Conference on the Engineering of Sport, Kyoto, Japan, 3–6 September 2002; Volume 20. [Google Scholar]
- Lorenz, R.D. Flight and Attitude Dynamics Measurements of an Instrumented Frisbee. Meas. Sci. Technol. 2005, 16, 738. [Google Scholar] [CrossRef]
- Koyanagi, R.; Ohgi, Y. Measurement of Kinematics of a Flying Disc Using an Accelerometer. Procedia Eng. 2010, 2, 3411–3416. [Google Scholar] [CrossRef]
- Fuss, F.K.; Doljin, B.; Ferdinands, R.E.D.; Beach, A. Dynamics of spin bowling: The normalized precession of the spin axis analysed with a smart cricket ball. Proc. Eng. 2015, 112, 196–201. [Google Scholar] [CrossRef][Green Version]
- Doljin, B.; Fuss, F.K. Development of a smart cricket ball for advanced performance analysis of bowling. Proc. Technol. 2015, 20, 133–137. [Google Scholar] [CrossRef]
- Fuss, F.K.; Doljin, B.; Ferdinands, R.E.D. Effect of the grip angle on off-spin bowling performance parameters, analysed with a smart cricket ball. Proceedings 2018, 2, 204. [Google Scholar] [CrossRef]
- Fuss, F.K.; Doljin, B.; Ferdinands, R.E.D. Effect on Bowling Performance Parameters When Intentionally Increasing the Spin Rate, Analysed with a Smart Cricket Ball. Proceedings 2018, 26, 226. [Google Scholar] [CrossRef]
- Fuss, F.K.; Smith, M.R. Development of a smart oval ball for assessment of angular flight dynamics and precision of kick execution. Sports Technol. 2011, 4, 151–158. [Google Scholar] [CrossRef]
- Fuss, F.K.; Smith, M.R.; Leali, F. Kick Precision and Spin Rate in Drop and Torpedo Punts. Procedia Eng. 2013, 60, 448–452. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weizman, Y.; Tan, A.M.; Fuss, F.K. Measurement of Flight Dynamics of a Frisbee Using a Triaxial MEMS Gyroscope. Proceedings 2020, 49, 66. https://doi.org/10.3390/proceedings2020049066
Weizman Y, Tan AM, Fuss FK. Measurement of Flight Dynamics of a Frisbee Using a Triaxial MEMS Gyroscope. Proceedings. 2020; 49(1):66. https://doi.org/10.3390/proceedings2020049066
Chicago/Turabian StyleWeizman, Yehuda, Adin Ming Tan, and Franz Konstantin Fuss. 2020. "Measurement of Flight Dynamics of a Frisbee Using a Triaxial MEMS Gyroscope" Proceedings 49, no. 1: 66. https://doi.org/10.3390/proceedings2020049066
APA StyleWeizman, Y., Tan, A. M., & Fuss, F. K. (2020). Measurement of Flight Dynamics of a Frisbee Using a Triaxial MEMS Gyroscope. Proceedings, 49(1), 66. https://doi.org/10.3390/proceedings2020049066





