Abstract
Experimental analyses of motions of a double-leg circle were conducted for a smooth and dynamic movement. A motion capture system provided the data for two different gymnasts; one is well trained and the other has an average skill level. Lissajous analysis was done for a tip-toe circling motion and a rolling motion around a longitudinal axis of a body. The results show that synchronization between the tip-toe circling and the body-rolling around the body’s longitudinal axis is crucial. Muscle activity was also analyzed from electromyogram data when the gymnasts performed double-leg circles, and the muscle activity characteristics of synchronized rolling-type circles were uncovered.
1. Introduction
There are various ways to perform the double-leg circle, which is a basic movement on the pommel horse in gymnastics [1]. A major change in the performance of this activity involved moving from the hip-bending technique to the hip-straightening one [2]. With this change, a grander and more graceful performance can be achieved.
However, most double-leg circles are currently not always performed gracefully, although they are performed in a hip-straightening manner. They appear to reflect the basic problem of indecision with respect to which type of performance to exhibit; this problem can be analytically solved.
We previously proposed an evaluation method that uses the relationship between the tiptoe circling and hip rotation movement in double-leg circles [3]. To perform a smooth circular motion with a hip-straightening form, effectively rolling the body around the body’s longitudinal axis is crucial; this movement is referred to as a synchronized rolling-type circle in this paper. This evaluation method was employed to assess and compare the performance of two gymnasts, one performing a synchronized rolling-type circle and the other performing an asynchronized rolling-type circle; experimental data obtained from a motion capture system were evaluated. Furthermore, detailed analysis focusing on body rotation around the body’s longitudinal axis was conducted. From these results, the synchronized rolling-type circle characteristics were revealed. On the basis of electromyogram data, an analysis was conducted to determine muscle activity when performing double-leg circles. This analysis identified the muscle activity characteristics of synchronized rolling-type circles.
2. Evaluation Method
Figure 1a illustrates the performance of a double-leg circle in which the gymnast circles clockwise from an ideal geometrical point of view. The tiptoe moves in a circular orbit with its center on a vertical line or z-axis passing through the center of the pommel horse body.
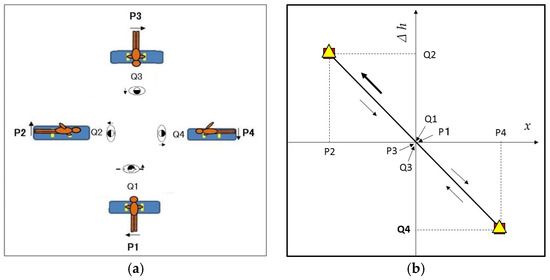
Figure 1.
(a) Performance of double-leg circle (b) Lissajous diagram from the ideal geometrical point of view.
The origin of the coordinates is the floor surface below the center of a pommel horse body. The x-axis is the longitudinal direction of the horse body, and the y-axis is perpendicular to the x-axis on the horizontal plane.
In Figure 1a, the symbols P1–P4 designate tiptoe positions for x = 0 or the circling angle = 0°, y = 0 or the circling angle = 90°, x = 0 or the circling angle = 180°, and y = 0 or the circling angle = 270°, respectively.
The performance of double-leg circles is associated with counterclockwise rotation around the body’s longitudinal axis. In Figure 1a, the body’s rotational postures are displayed from a head to tiptoe direction indicated by the symbols Q1, Q2, Q3, and Q4. As the body turns around its longitudinal axis counterclockwise, the rotation angle of the direction of both hips changes from 0° at Q1 to −90° at Q2, −180° at Q3, and −270° at Q4.
The figure indicates that the Q1–Q4 positions coincide with those of P1–P4, respectively. Therefore, the tiptoe-circling motion and hip rotation synchronize with respect to the absolute values of circling and rotation angles. In a real performance, this synchronization is not always achieved because crossing over both the pommel and end of the horse body on either the right or left side in a smooth motion is difficult. Overcoming this difficulty requires key skills in synchronizing the tiptoe-circulating motion and hip rotation.
Figure 1b illustrates the synchronization analyzed with respect to the relationship between the x-axis value of the tiptoe position in the abscissa and the height difference from the left to right hip, Δh, in the ordinate. The synchronization is expressed by a straight line in the ideal double-leg circle. This type of figure is a Lissajous figure. The path in the second quadrant of the Lissajous double-leg circle is in the “flank in” phase, and the path in the fourth quadrant is in the “flank out” phase.
3. Experiment
To analyze double-leg circle performance, two gymnasts were selected. They were designated Gymnasts A and B. Gymnast B was trained by Yamawaki, one of the authors, so as to rotate as constantly as possible around the longitudinal axis of the body, while performing the tiptoe circling motion, especially during the flank in and the flank out phases. On the other hand, Gymnast A was not trained to perform the exercise in this manner.
Motion capture measurements were conducted on the movements of these gymnasts by using the following measuring points (each point has a right- and left-side marker): 35 points were applied to body parts, namely the wrist, shoulder, breast, hip, and tiptoe; and 18 points were analyzed for myoelectric potential and applied to the trapezius, latissimus dorsi, obliquus externus abdominis, adductor magnus, rectus femoris, and biceps femoris.
The markers were recorded at a rate of 200 frames/s by 12 video cameras fixed over the pommel horse. The sampling rate for myoelectric potential was 1 kHz, which synchronized with the video image. The muscle activities were integrated every 5 ms and normalized according to the maximal voluntary contraction of every muscle.
Motion analysis was conducted using an assumed model with a set of mass properties consisting of mass, center of mass, or center of gravity (here after COG), and the inertia tensor of each segment of the body. In total, 51 segments were recorded. Mass properties were computed from the simplified segment shapes by using spheres, cylinders, and cones and adopting a constant density. The kinematic model comprised tree-structured rigid-body segments connected by spherical joints. For this analysis, only the time-dependent coordinates of the entire body’s COG were used.
4. Comparison of the Performances by Gymnasts A and B
4.1. Height of the Center of Gravity and Lissajous Figure
Figure 2a,b illustrate the vertical movement of the COG of Gymnasts A and B, respectively. The horizontal axis represents time, t, and the vertical axis represents the COG height, z, from the floor. The bold line represents a height of 1500 mm from the floor as reference. A period for one cycle is 988 ms for gymnast A and 880 ms for gymnast B. as shown in each figure caption. Then, the rotational speed of Gymnast B was faster than that of Gymnast A.
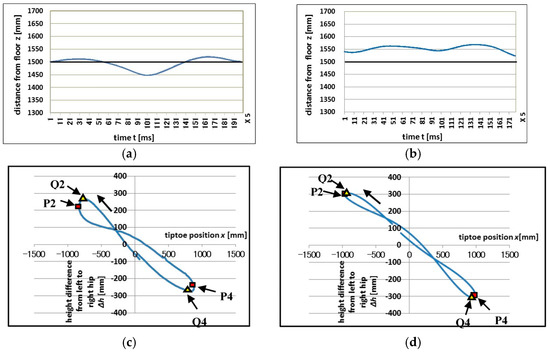
Figure 2.
(a) Vertical movement of COG, Gymnast A (Period for one circle is 988 ms); (b) Vertical movement of COG, Gymnast B (Period for one circle is 880 ms); (c) Lissajous diagram, Gymnast A [3]; (d) Lissajous diagram, Gymnast B.
It is seen in the figure that the average height of COG for Gymnast B was higher than that of Gymnast A, and that the height variation of COG for Gymnast B is smaller than that of Gymnast A. This difference seems to come from the difference in the rotational speed of the double-leg circles. It can be said that Gymnast B exhibits smoother and more dynamic performance than that of Gymnast A.
Figure 2c,d present the Lissajous figures for double-leg circle performances by gymnast A and B, respectively. A large bulge is evident in the fourth quadrant for Gymnast A. This signifies that hip rotation was delayed relative to tiptoe circling motion in the flank out phase. On the other hand, the large bulge in the second quadrant indicates that the hip rotation progressed earlier than the tiptoe rotation. In this process, the delay in the later part of the flank out phase was rapidly recovered in the early part of the flank in phase. This rapid motion enabled the gymnast to catch up with the rotation by adjusting one hip rotation to one tiptoe-circling motion. In contrast to Gymnast A, Gymnast B’s Lissajous exhibits no large bulge in the second or fourth quadrants. Gymnast B’s Lissajous is approximately a straight line, which indicates that the hip rotation and tiptoe-circling motion were synchronized. In addition, sudden hip rotations were not observed during the synchronized motion, and this resulted in smoother double-leg circle performance.
4.2. Hip Rotation Angle
Figure 3a,b display the time history of the hip rotation angles of Gymnasts A and B, respectively. The horizontal axis represents time normalized by one double-leg circle period. The vertical axis represents the angle of hip rotation in degree. The green lines indicate constant angular velocity or average angular velocity as a reference line.
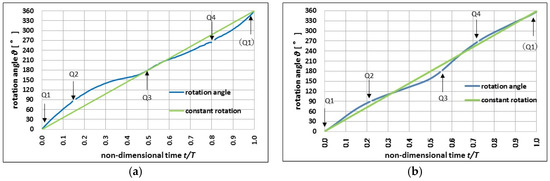
Figure 3.
Time history of rotation angle around the body axis. (a) Gymnast A; (b) Gymnast B.
Figure 3a,b indicate that rotation angle deviations from the straight line for constant angular velocity are considerably larger for Gymnast A than those for Gymnast B. This may explain why Gymnast A’s movement was not synchronized but that of Gymnast B was. Constant rotation around the longitudinal axis of the body is critical factor in synchronized double-leg circles, as well as the constant angular velocity of the tiptoe-circling motion is essential.
4.3. Twist Angle between Upper and Lower Body
Thus far, we have discussed only hip rotation and have yet to consider the entire body because hip rotation does not necessarily signify upper body rotation. To examine this condition, the twisting motion was investigated.
The body is separated into two parts: The upper and lower body. The twisting motion between these two parts was investigated. The upper body is represented by a triangle plane formed by the edge of both shoulders and the midpoint of the hips. The lower body is represented by a triangle plane formed by the edge of both hips and the midpoint of the tiptoes. We calculated the twist angle Δα between these two planes.
Figure 4 shows time histories of the change in Δα. In the figure, the horizontal axis represents nondimensional time, and the vertical axis represents Δα in degree, which is positive when the lower body is twisted counterclockwise against the upper body. Hip rotation precedes upper body changes when this value is positive, and hip rotation follows upper body changes when the value is negative.
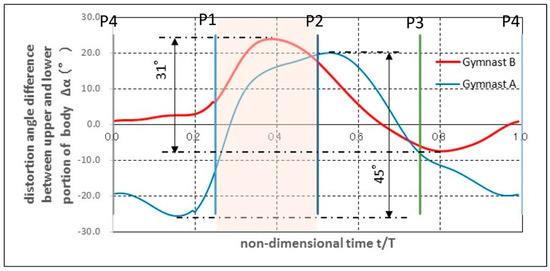
Figure 4.
Distortion angle between the upper and lower body.
It is observed in the figure that for Gymnast B, the twisting angle is 0° during the later part of the flank out phase (P4). By contrast, this angle is seen to be −20° for Gymnast A. During this phase, Gymnast B experienced no twisting between the upper and lower bodies. However, Gymnast A’s upper and lower bodies twisted from each other, which delayed the hip rotation.
The next action of both gymnasts is preparation for the flank in phase, as indicated in the pink area of Figure 4. It is seen that in this phase, Gymnast A recovers from the delayed hip rotation (Δα < 0) y twisting his lower body into the non-twisting condition Δα = 0 and proceeds to rotate his hips in advance of tiptoe rotation (Δα > 0). To achieve this matching (one hip rotation for one tiptoe rotation), a steep change in twisting is seen from P1 to P2 with a negative value to a positive value. On the other hand, Gymnast B exhibits only a small value of Δα during P4 to P1 period and hardly needs to rotate his lower body for recovery, executing moderate twisting from P1 to P2 in advance of tiptoe rotation. As indicated in the figure, the swings in Δα is 45° for Gymnast A and 31° for Gymnast B.
It can be said that Gymnast B continues his performance with less twisting than Gymnast A does in overall double-leg circle performance. Thus, Gymnast B performed the rolling movement around his body by maintaining a nearly straight posture.
4.4. Muscle Activity
Murai et. al [4] pointed out the important role of the external oblique muscle in performing a double-leg circle. We also focused on the external oblique muscle, which appeared to be closely related to hip-rolling movements. Figure 5a,b display the behavior of the external oblique muscle. In each figure, the axis represents the time for one double-leg circle cycle, and the vertical axis represents muscle activity. In each figure, P1–P4 are represented by vertical straight lines. Short lines signify Gymnast A, and long lines signify Gymnast B. Because the rotation direction differed between Gymnasts A and B, comparing muscle activity depicted in the same figure required that the data for Gymnasts A and B change. For Figure 5a, the graph shows the left muscle activity of Gymnast A and the right muscle activity of Gymnast B.
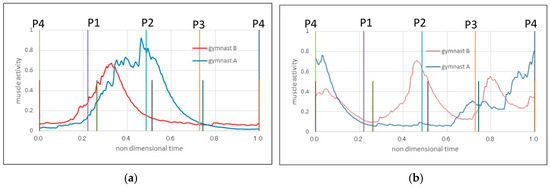
Figure 5.
Muscle activity of the external oblique muscle of Gymnasts A and B. (a) Left side; (b) Right side.
By comparing Figure 5a with Figure 4, which indicates the distinct feature of the hip twisting motion, it is evident the graph trend in Figure 5a is very similar to that in Figure 4: both gymnasts peaked between P1 and P2, with little time difference.
By comparing Figure 5b and Figure 3, a relationship between the acceleration of hip rotation and muscle activity is observed. For example, for Gymnast B, the doubled acceleration at Q2 and Q4 in Figure 3 appears to be caused by the muscle activity peak at P2 and P4 depicted in Figure 5b. However, for Gymnast A, such a relationship was not observed.
5. Conclusions
By comparing two gymnasts, one performing a synchronized rolling-type double-leg circle and the other performing an asynchronized one, the following synchronized rolling-type double-leg circle features were revealed:
- (1)
- Fast tiptoe circling speed and high COG position facilitate the synchronized rolling-type double-leg circle performance.
- (2)
- The rolling movement around the synchronized gymnast’s body is performed with less twisting between the upper and lower body in overall synchronized double-leg circle compared with an asynchronized one.
- (3)
- Electromyogram data analysis of gymnasts performing a synchronized rolling-type double-leg circle indicates that the external oblique muscle is involved in the hip rotation acceleration and the twisting motion.
References
- Nawa, M.; Nishiwaki, K.; Yamawaki, K.; Iegami, Y.; Nakamura, Y.; Murai, A.; Ayusawa, K.; Yamasaki, T. The mechanism of a double-leg circle on a pommel horse, and its variation of performance. In Proceedings of 2015 Conference on Sports Engineering and Human Dynamics; Japan Society of Mechanical Engineers: Tokyo, Japan, 2015; p. C-3. (In Japanese) [Google Scholar]
- Sano, T.; Watanabe, Y. A study of trends in the historical development of elements and techniques related to two-leg systems on the pommel horse. Jpn. J. Phys. Educ. Health Sport Sci. 2019, 64, 501–519. (In Japanese) [Google Scholar] [CrossRef]
- Nawa, M.; Nishiwaki, K.; Yamawaki, K.; Ikegami, Y.; Nakamura, Y.; Murai, A.; Ayusawa, K.; Yamasaki, T. An evaluation of performance of a double-leg circle on a pommel horse, and a desirable performance proposal. In Proceedings of the 19th International Conference on Biomechanics in Sports (ISBS-2016 Tsukuba), Tsukuba, Japan, 18–22 July 2016. Paper No. P0621374. [Google Scholar]
- Murai, A.; Ayusawa, K.; Nakamura, Y. Dynamics and biomechanical analysis of circles on pommel horse. In Proceedings of 2013 Conference on Sports Engineering and Human Dynamics; Japan Society of Mechanical Engineers: Tokyo, Japan, 2013; p. 316. (In Japanese) [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).