Abstract
Soccer/football is one of the most popular sports in the world. Any sport requires continuous adjustments to rules to keep the game safe and engaging. Increased awareness of concussions in the American National Football League (NFL) has consequently raised attention to concussion-related injuries in other sports. One of the first steps the United States Soccer Federation (USSF) has taken to reduce head injuries is to implement age restrictions on heading. This encourages safer play but discourages an important skill until players are a certain age which is not good for player development. An alternative is to ensure mean head acceleration from a header is reduced with minimal rule changes. This paper presents a dynamic model of a player heading a soccer ball to examine the general relationship between ball pressure and mean head acceleration toward the purpose of motivating a more complex and comprehensive analysis of heading in soccer.
1. Introduction
Soccer is one of the most popular sports in the world. Head injuries in the sport are more prevalent at the professional level, but the concern about concussions extends to recreational and young players as well. One way that US Youth Soccer has tried to mitigate this issue is by strongly suggesting that leagues ban heading for players below a certain age (U12, U11, U10 being most common). While most concussions in soccer are due to head-to-head collisions deemed legal under the current rules in place [1], some evidence suggests that engaging in headers at a young age may cause minor head injuries which exert their effects in a cumulative fashion over time [2]. However, it is important to note that there is no evidence so far to prove that heading as a youth player will directly cause problems later on. While there have been various studies on concussions in professional soccer players [3,4], there has only recently been research on younger athletes [5]. Previous studies have identified the mass of the ball relative to the player as a factor in the head acceleration, indicating younger athletes may be more at risk, even when using smaller size balls. The previous study by Babbs, however, does not consider the dynamics of the player’s head. Rather, Babbs models the entire player as a single rigid body. This paper will consider using a lumped mass model for the head to capture the significant variation in neck strength/stiffness in youth players, which may result in even more extreme head accelerations. FIFA laws state that the air pressure in a regulation ball must be between 8.5 psi and 15.6 psi. A deterministic study of men, women and youth players heading balls is followed by Monte Carlo simulations, focusing on youth players, in order to understand how the acceleration of the head changes as the pressure in the ball changes.
2. Materials and Methods
A simplified lumped mass dynamic model was proposed to capture the important dynamics of a soccer player heading a soccer ball, as illustrated in Figure 1:
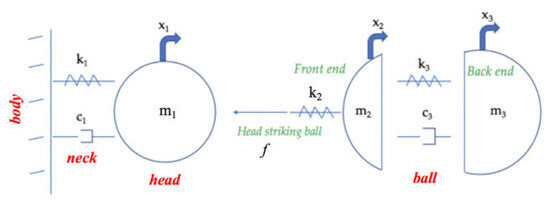
Figure 1.
Proposed lumped mass representation of a soccer ball impacting a player’s head.
From Newton’s second law, the dynamic set of equations of motion of the system shown in Figure 1 can be written as:
where m1 is the mass of the player’s head, m2 is the mass of the deformed portion for the ball during impact, m3 is the mass of the remainder portion of the ball, k1 and c1 are the stiffness and damping of the player’s head, k3 and c3 are the stiffness and damping of the ball between the two ball masses, and f is the force the head applies to the front end of the soccer ball. The mass of the soccer ball, m, is related to masses m2 and m3 through mass ratio μ as:
The stiffness of the soccer ball is determined from the natural frequency of a ball, f3, estimated to be 150 Hz [6]. As such the stiffness, k3, is determined as
The stiffness of the player’s head is determined from prior research identifying the rotational stiffness of men, women and youth necks to applied moments [7]. The linear stiffness, k1, is then determined, with an estimate of the length from the neck rotation to location on the head that strikes the ball, r = 25.4 cm, as
Linear viscous damping is assumed for the damping coefficients such that:
where z1 and z2 are the damping ratios for the head and ball, respectively, and and are the circular natural frequencies of the ball and head, respectively. The force the front end of the ball applies to the head, f, can be defined by the nonlinear function as:
where the stiffness k2 of the head acting on the ball is set to the same internal stiffness of the ball, k3, and when x2 is larger than x1 (the otherwise case in Equation (8)), the head is no longer in contact with the front end of the ball.
The equations of motion in Equations (1)–(3) can be solved simultaneously in MATLAB Simulink while simulating the interface force in Equation (8). The parameters are identified from various prior research and the values selected for this study are given in Table 1.

Table 1.
Values for header simulation.
It is assumed that the air pressure in a soccer ball, p, affects both the stiffness and damping of the ball. The stiffness of the ball, k3, at the prescribed air pressure is determined from Equation (5) such that . Babbs [5] showed that the ball stiffness is equal to the product of the air pressure and the circumference of the ball. As such, k3 is directly proportional to air pressure, with the baseline at 10 psi.
The relationship between the pressure and damping of a soccer ball is more complex. While it is reasonable to assume that the damping of the ball is inversely related to the pressure, an experiment was designed in the author’s prior research [8] to better quantify this relationship. In the experiment, balls of varying ball pressure are dropped from a fixed height,, and the height of the first rebound, y1, is measured such that the coefficient of restitution (CoR), , can be calculated. The damping ratio, shown by Nagurka and Huang [6] depends only on the CoR, determined as:
From this study the damping ratio of the ball is found to be a second order function of the ball pressure as
We are mostly concerned with headers which mostly occur as the y-component of the ball’s flight as negative. In this paper, soccer ball speeds of 6.7, 6.7, and 7.6 m/s are used for male, female, and youth, respectively, with a standard deviation of 2.2 m/s for all cases. Goldstein used values for the weight of a human head in a helmet study between 35.6 and 53.4 N (8 and 12 pounds) on average [9]. By the age of 5, the skull has grown to over 90% of the adult size [10]. While head mass might be surprisingly similar between children and adults, it is important to note that the neck stiffness in children is only 50% that of its adult value [11]. McGill found flexion stiffnesses for adult males and females [7] which we will use for our program. Additionally, in this paper, we used head masses of 44.5, 44.5 and 40.0 N (10, 10 and 9 lbs) for male, female, and youth, respectively, with a standard deviation of 1.5 lbs for all.
3. Results/Discussion
The simulation is conducted for a typical male soccer player and a standard ball pressure of 10 psi. The results are shown in Figure 2. The ball is given an initial velocity of −6.7 m/s. The simulation begins (t = 0) when the ball and head initiate impact. The impact lasts approximately 13.7 m/s, before the ball leaves the player’s head. It is observed that the displacement of the front and back ends of the ball have a relative displacement during the impact, and after leaving the head, they move away from the head and converge. The head is displaced backward during heading. The velocity of the front and back ends of the ball are initially at −6.7 m/s and during the header, the front end of the ball oscillates more predominantly than the back end. After leaving the head, the front and back ends converge to a constant velocity of 5.3 m/s. The dynamics of the head are less noticeable in the displacement and velocity responses. However, the acceleration response clearly shows the head dynamics in play as the acceleration oscillates during the impulsive event, reaching a peak acceleration of 11.54 g. Of importance to concussive injuries is the mean acceleration [5], the average acceleration over the duration of the ball impact. For the example shown in Figure 2, the mean acceleration is 6.04 g. These simulation results are verified through comparison to the simulation results in [5], whereby the displacement magnitudes and time duration of impact are consistent. Further experimental verification would be beneficial.
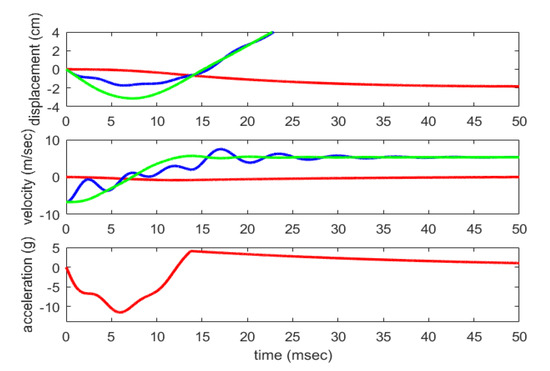
Figure 2.
The effect of a ball pumped to 10 psi on the displacement of ball (blue and green) and head (red), the velocity of ball (blue and green) and head (red), and the acceleration of a head for a male heading a soccer ball.
Simulations are conducted for male, female, and youth players and for soccer balls at various pressures. Figure 3a shows the time histories for a header for these three different player types. It is evident that the peak acceleration for a youth head is larger than that of a female or male head which are relatively similar. The peak accelerations of the male, female and youth players heading their respective soccer balls are 11.54 g, 11.80 g, and 12.27 g, respectively. The mean accelerations of the male, female and youth players heading their respective soccer balls are 6.04 g, 6.33 g, and 6.77 g, respectively. The female player experiences a 4.9% increase in mean head acceleration from the male player, while the youth player experiences an 11.2% increase in mean head acceleration over the male player. Figure 3b shows the time histories for a header for a youth player at three different ball pressures; one at the lowest end of the FIFA range (8.5 psi), one in the middle (10 psi), and one at the maximum pressure in the FIFA range (15.6 psi). The peak accelerations for the 8.5 psi, 10 psi, and 15.6 psi pressures are 11.08 g, 12.27 g, and 15.90 g, respectively. The mean accelerations for the 8.5 psi, 10 psi, and 15.6 psi pressures are 6.11 g, 6.77 g, and 8.880 g, respectively. Over the FIFA pressure range, this is a 45.3% increase in mean head acceleration. Even larger increases in mean head acceleration (49.9% and 47.6%) are observed for the male and female players as the ball pressure increases from the minimum FIFA pressure of 8.5 psi to maximum FIFA pressure of 15.6 psi.
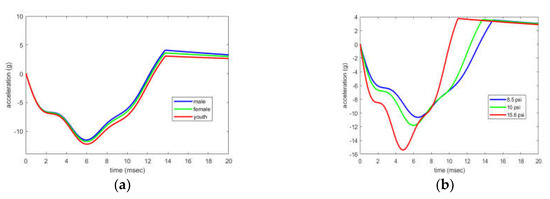
Figure 3.
The effect of a ball pumped to 10 psi (a) on the displacement of the head of men, women, and youth and the effects of different ball pressures (b) within the FIFA range on the acceleration n of the head in youth. Peak accelerations for the 8.5 psi, 10 psi, and 15.6 psi are 11.12 g, 12.31 g, and 15.92 g respectively.
Considering the variability in the speed of the ball and properties of the player’s head, Monte Carlo Simulation (MCS) is used to capture the variability in the resulting mean head acceleration. Considered here are random variables for ball speed, head mass, and neck stiffness for youth in order to capture the variation for the mean head acceleration across different scenarios. Figure 3a shows a histogram of the results of 10,000 simulations of a youth player heading a soccer ball pumped to a pressure of 10 psi. The ball speed range for these simulations was from −0.2 m/s to −15.5 m/s. It is observed that the probability of a header event exceeding a mean acceleration of 10 g is 10%. Figure 4b shows the results of a series of MCSs conducted for the youth player at various levels of ball pressure, where the probability of exceeding a mean head acceleration of 10 gs is shown. Babbs [5] suggests the use of mean head acceleration during impact and the authors propose that mean head accelerations under 10 gs can be considered ‘safe’. At 8.5 psi, 10 psi and 15.6 psi, the probabilities of exceeding 10 g are 4.7%, 9.2%, and 35.5%, respectively. This indicated over a 30% increase in the probability of a youth player heading a ball exceeding 10 g mean acceleration over the FIFA specified ball pressure range.
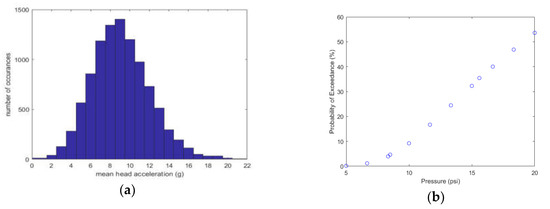
Figure 4.
A histogram (a) showing the distribution of peak head accelerations through a Monte Carlo simulation with random variables for ball speed, head mass, and neck stiffness for youth. Also from the Monte Carlo simulation, is the probability (b) that a certain mean head acceleration exceeds (10 g).
4. Conclusions
A computational model for heading the soccer ball is developed and a simulation is conducted showing the extent to which youth are more susceptible to injuries from headers. Youth mean head acceleration is 11.2% larger than adult male mean head acceleration. There is a 45.3% increase in mean head acceleration over the specified FIFA pressure range. When considering the variation in ball speed and player’s heads, it is observed that over the FIFA pressure range, from 8.5 psi to 15.6 psi, the probabilities of mean head acceleration exceeding 10 g are 5% and 35%, respectively. Further analytical, laboratory and field studies are warranted to further explore the effect of ball pressure on the safety of heading in the game of soccer.
References
- Patlak, M.; Institute of Medicine. Is Soccer Bad for Children’s Heads?: Summary of the IOM Workshop on Neuropsychological Consequences of Head Impact in Youth Soccer; The National Academies Press: Washington, DC, USA, 2002. [Google Scholar]
- Bunc, G.; Ravnik, J.; Velnar, T. May Heading in Soccer Result in Traumatic Brain Injury? A Review of Literature; Clinical Department of Neurosurgery, University Medical Centre: Maribor, Slovenia, 2017. [Google Scholar]
- Coffew, N.; Lawless, M.; Kelly, S.; Buggy, C. Frequency of Self-Reported Concussion Amongst Professional and Semi-Professional Footballers in Ireland During the 2014 Season: A Cross-Sectional Study. Sports Med.-Open 2018, 4. [Google Scholar] [CrossRef] [PubMed]
- Does Heading Soccer Balls Hurt Women’s Brains? US Soccer stars Take Part in New Study. Available online: https://www.nbcnews.com/health/health-news/does-heading-soccer-balls-hurt-women-s-brains-u-s-n1071621 (accessed on 14 November 2019).
- Babbs, C.F. Biomechanics of Heading a Soccer Ball: Implications for Player Safety. In Weldon School of Biomedical Engineering Faculty Publications; Hindawi: London, UK, 2001; p. 34. [Google Scholar]
- Nagurka, M.; Huang, S. A Mass-Spring-Damper Model of a Bouncing Ball. Int. J. Eng. Educ. 2006, 22, 393–401. [Google Scholar]
- McGill, S.M.; Jones, K.; Bennett, G.; Bishop, P. Passive stiffness of the human neck in flexion, extension, and lateral bending. Clin. Biomech. 1994, 3, 193–198. [Google Scholar] [CrossRef]
- Christenson, A.; Cao, P.; Tang, J. Optimal Football Pressure as a Function of a Footballer’s Physical Abilities. In Proceedings of the 12th Conference of the International Sports Engineering Association, Brisbane, Queensland, Australia, 26–29 March 2018. [Google Scholar]
- Goldstein, J.P. The effect of motorcycle helmet use on the probability of fatality and severity of head and neck injuries. Eval. Rev. 1986, 10, 355–375. [Google Scholar] [CrossRef]
- Huelk, D.F. An Overview of Anatomical Considerations of Infants and Children in the Adult World of Automobile Safety Design. Assoc. Adv. Automot. Med. 1998, 42, 93–113. [Google Scholar]
- Lavallee, A.V.; Ching, R.P.; Nuckley, D.J. Developmental biomechanics of neck musculature. J. Biomech. 2013, 46, 527–534. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).