Applicability of Thermoplastic Elastomers to Impact Load Reduction in Sports Equipment ^†

Abstract

In this paper, mechanical properties of thermoplastic elastomers were investigated to expand the applicability of thermoplastic elastomers to the impact load reduction for the sports equipment. The thermoplastic elastomers show both thermoplastic and elastomeric properties. These are expected to apply to the impact load reduction in sports equipment due to good processability and less-smell. In this study, thermoplastic elastomers were applied for monotonic and cyclic tensile loading tests. The thermoplastic elastomer (TPE) materials in this study were newly developed for the specific purpose of impact load reduction. The nonlinear hyperelastic model considering the viscosity and damage model was applied to the tensile loading test results. finite element analysis (FEA) results of TPE specimens with periodic geometric shapes to reduce impact load were investigated.

1. Introduction

In this paper, mechanical properties of thermoplastic elastomers (TPEs) were investigated to expand the applicability of the TPEs to the impact load reduction for the sports equipment. The finite element analysis (FEA) of thermoplastic elastomer specimens was conducted to evaluate the applicability of the TPEs to the impact reduction in sports equipment. Foaming materials like polyurethane have been applied to face guards, headgears and catcher’s chest protectors [1,2,3]. The foaming materials in these sports protectors show higher stiffness due to consolidation under a larger impact load.

TPEs show the mechanical properties of both rubber and plastic materials. The design of stiffness and viscous properties of TPEs is possible to adjust under the requirement of higher impact load in sports. Thus, impact load reduction in sports equipment is one of the main expected applications of the TPEs due to having good processability and a reduced smell.

In this study, thermoplastic elastomers were applied for monotonic and cyclic tensile loading tests. The TPE materials in this study were newly developed for the specific purpose of impact load reduction. The nonlinear hyperelastic model considering viscosity and damage model was applied to the tensile loading test results. FEA results of TPE specimens with periodic geometric shapes to reduce impact load were investigated.

2. Materials and Methods

In this study, the viscoelastic model with a damage model were applied to the FEA simulation, in order to reproduce the mechanical properties of TPEs. The following elastic energy function for the incompressible visco-elastic material has been applied to the TPEs in this study [4,5]:

$$W\left(\overline{\mathit{C}},{\Xi }^m,{\mathit{Q}}_i\right)={\overline{W}}^0\left(\overline{\mathit{C}},{\Xi }^m\right)-{\displaystyle \sum }_{i=1}^{N_d}\frac{1}{2}\overline{\mathit{C}}:{\mathit{Q}}_i$$

(1)

where $W$ is the elastic energy function, the symbol ${\left(\right)}^0$ means the elastic component, ${\overline{W}}^0$ is the elastic energy function of deviation component of the hyperelastic constitutive equation, ${\Xi }^m$ is the internal variable for a damage function like the Mullins effect, ${\mathit{Q}}_i$ is the viscous stress and $N_d$ is number of the dashpots. $\overline{\mathit{C}}$ is the volume-preserved right Cauchy-Green tensor calculated as $\overline{\mathit{C}}=J^{-\frac{2}{3}}{\mathit{F}}^T\mathit{F}$. $\mathit{F}$ and $J$ are the deformation gradient tensor and the determinant of the deformation gradient tensor $\mathit{F}$, respectively.

From the cyclic tensile loading test results, the stress-strain relationships of the TPEs were confirmed to depend on the maximum stretch [5]. To represent this behavior, the following elastic potential function was applied to elastic part of TPEs:

$$\begin{gathered} {\overline{W}}^0\left(\overline{\mathit{C}}, {\Xi }^m\right)=g\left({\Xi }^m\right)\overline{W}\left(\overline{\mathit{C}}\right) \\ =g\left({\Xi }^m\right)\left\{C_{11}\left({\overline{I}}_1-3\right)+C_{12}{\left({\overline{I}}_1-3\right)}^2+C_{21}\left({\overline{I}}_2-3\right)\right\}. \end{gathered}$$

(2)

$\overline{W}\left(\overline{\mathit{C}}\right)$ is the pure elastic energy without damage of the TPEs. The damage function $g\left({\Xi }^m\right)$ was introduced as an exponential form as follows:

$$g\left({\Xi }^m\right)=\beta +\left(1-\beta \right)\frac{1-\exp \left(-{\Xi }^m/\alpha \right)}{{\Xi }^m/\alpha }.$$

(3)

The internal variable $\Xi$ was given by the following equation [5]:

$$\Xi =\sqrt{2\overline{W}\left(\overline{\mathit{C}}\right)}.$$

(4)

Now, let ${\Xi }^m$ be the maximum value of $\Xi$ over the past history up to the current time. Here, $\alpha$ and $\beta$ are material parameters of the damage model. From the cyclic tensile loading test results, material parameters $C_{11}$, $C_{12}$ and $C_{21}$ were determined as 0.555 MPa, −0.003 MPa, 0.22 MPa, respectively. The parameters of viscosity were determined as $N_d=2$, ${\gamma }_1=0.34, {\tau }_1=12\mathrm{s}$, ${\gamma }_2=0.12, {\tau }_2=350\mathrm{s}$, respectively. Also, the parameters of damage model $\alpha$ and $\beta$ were determined as 0.735 and 0.0243. The 2nd Piola-Kirchhoff stress is given by the partial derivative of $W\left(\overline{\mathit{C}},{\Xi }^m,{\mathit{Q}}_i\right)$ with respect to the right Cauchy-Green tensor $\mathit{C}$ as follows:

$$\mathit{S}=2\frac{\partial W\left(\overline{\mathit{C}}, {\Xi }^m, {\mathit{Q}}_i\right)}{\partial \mathit{C}}.$$

(5)

3. Results and Discussion

The monotonic tensile loading tests and the cyclic tensile loading tests were conducted to evaluate the mechanical properties of TPEs. First, monotonic tensile loading tests on the TPE specimens were conducted using a uniaxial tensile loading machine. The strain rates of tensile loading tests were set to 0.1%/s, 1.0%/s and 10%/s, respectively. Figure 1 shows the relationship between stress and strain given by the tensile loading test and the proposed viscoelastic model.

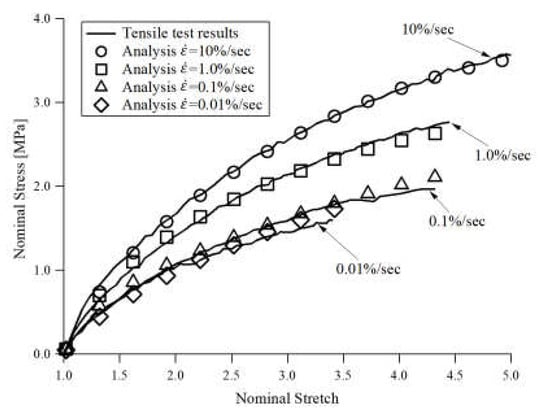
Figure 1. Tensile loading test results of thermoplastic elastomer (TPE).

The cyclic tensile loading tests of which stretch for cyclic deformations were 150%, 200% and 250% were conducted. Four cycle of deformation were applied to the tensile specimen continuously and the maximum stretch was increased from 150% to 250%. The cyclic loading test results of which the strain rate is 10%/s for the first cycle and the third cycle are shown with theoretical calculation obtained by the proposed viscoelastic model in Figure 2. Calculated results given by the proposed viscoelastic model show good agreement with the tensile loading test results and cyclic loading test results.

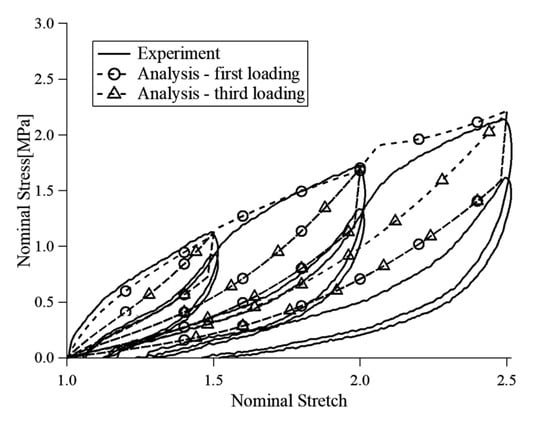
Figure 2. Cyclic tensile loading test results (Strain rate = 10%/s.).

Drop weight impact testing method is the major method to investigate the dynamic properties of materials. It is also applicable to the TPEs in high strain rate [6,7,8,9]. This test method is good for obtaining the dynamic properties of materials but is difficult to use to obtain microscopic-deformation or stress-distribution of materials. Thus, four kind sof FEA models for the TPE specimens which have a periodical hole structure were prepared (Figure 3). Geometrical shapes of the specimens were determined while considering the impact loading test facilities by using a real baseball ball, as shown in Figure 4 [10]. The size of all the FE models was 50 mm × 50 mm × 8 mm. These specimens were developed to apply to the load-reduction material in the catcher’s chest protectors. The relative density $\mathsf{\rho }$ of specimens A, B, C and D were 100%, 50%, 37% and 25%, respectively. The diameter of holes in the specimen B, C and D were just 10 mm, a set of 5 mm and 10 mm and a set of 7 mm and 10 mm, respectively. The boundary condition of FE analysis is shown in Figure 5. All nodes of bottom surface of specimens were constrained and nodes in the virtual baseball ball were also constrained to represent contact of the baseball ball to the TPE specimens. The number of elements of TPE specimens A, B, C and D were 2500, 2680, 2880 and 3240, respectively. The speed and diameter of the virtual baseball ball was assumed to be 0.8 mm/s and 74 mm, respectively. Displacement of 10 mm in the vertical direction was applied to the center of the virtual baseball ball under a quasi-static condition. Mean stress contributions of FE analysis are shown in Figure 6. Relationships between vertical load and displacement were shown in Figure 7. The simulated results were calculated under the viscous effect of the TPE which is shown in Figure 1 and Figure 2. The strain rate of all simulated results was 10%/s, which was same as the cyclic tensile loading test results shown in Figure 2. The speed of the virtual ball in the FEA was assumed to correspond to the same strain rate of cyclic tensile loading test shown in Figure 2, and differed from the drop weight impact test [10]. From the load-displacement relationships, stiffness reduction of the TPE specimens caused by the periodical holes were confirmed. From Figure 6, impact load reduction can be expected because the periodic hole structures cause deformation of the TPE.

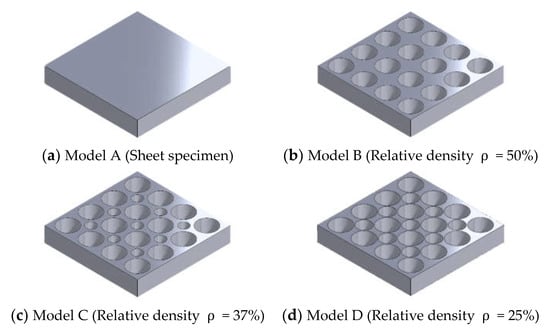
Figure 3. TPE specimens for finite element analysis (FEA).

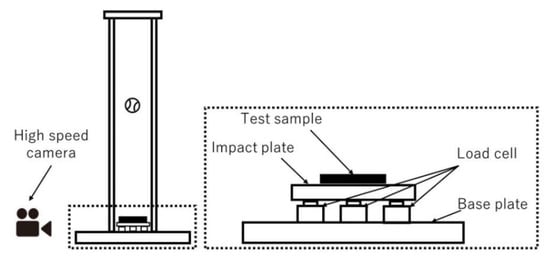
Figure 4. Drop weight impact test machine [10].

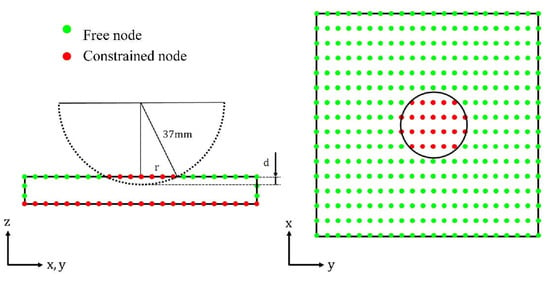
Figure 5. Boundary condition of FEA.

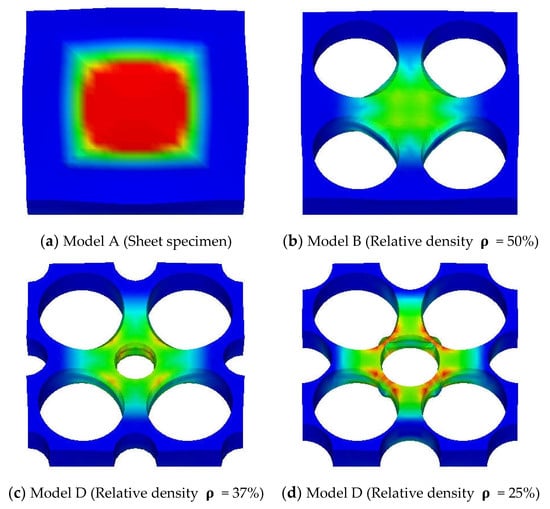
Figure 6. Stress distribution of FEA of TPE specimen.

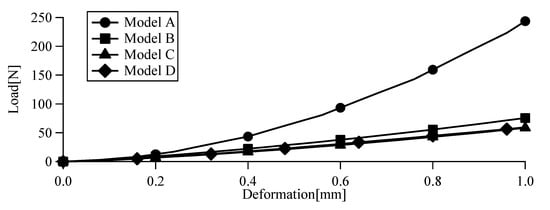
Figure 7. Relationships between deformation and load (Strain rate = 10%/s).

4. Conclusions

In this study, monotonic and cyclic tensile loading tests of TPEs and FEA simulation of TPE specimens with periodical holes were carried out to expand the applicability of TPEs to impact load reduction for sports equipment. FEA simulations of TPE specimens were conducted to investigate mechanical characteristics of TPE specimens with periodical structures. Stress distribution of each specimens were predicted by the FEA when the load was applied by a virtual baseball. The effect of the relative density of the TPEs and geometrical shapes of periodical holes on the mechanical characteristics of the TPE specimens were able to be predicted by the proposed viscoelastic model. The proposed structures are useful for applications in sports equipment because the periodic hole structure contributes to weight reduction.