Influence of Surface Properties on Soccer Ball Trajectories ^†

Abstract

In this paper, we summarize our recent research work on soccer balls. Employing wind tunnels and analyses of simulated trajectories, we have gained an understanding of how various surface features influence soccer ball aerodynamics. Wind tunnels provide aerodynamic coefficients for non-spinning soccer balls. The coefficients then help determine the trajectories of various simulated kicked balls. Surface features include panel texturing, seam width, and seam depth. We have determined that small changes in surface texturing can lead to hard-kicked soccer balls experiencing lateral deflections as large as 10%–20% of their horizontal ranges. We have also found that the critical Reynolds number for soccer balls is more strongly correlated with seam width than with seam depth.

1. Introduction

Sports such as baseball, basketball, and American football employ balls whose designs are rigidly specified by their respective governing bodies. In other words, players who participate in those sports use balls that feel and move the same throughout the players’ entire careers. Soccer, or Association Football, has no such standardized ball. Beyond specified ranges for circumference, mass, and internal pressure, a soccer ball may have a myriad of possible panel designs, seam characteristics, and panel texturing. Each installment of the World Cup sees a new ball that players must get used to prior to the start of the tournament because the ball will be different from what they used during their normal club games. Understanding how changes to a soccer ball affect the playing of the game is of interest to players, governing bodies, ball manufacturers, and sports fans who possess even a passing interest in the science of soccer.

For more than six years, the authors of this paper have collaborated in an attempt to understand how various surface properties of soccer balls influence their trajectories [1,2,3,4,5,6]. The manifestation of that influence resides in the aerodynamic coefficients associated with the components of the air’s force on a soccer ball as it moves along its trajectory. Air is treated as a continuous fluid at the macroscopic level. Modelling the air’s force on a soccer ball is challenging because of the complex ways in which the air’s influence on the ball changes from the ball’s surface to areas far from the ball. A boundary layer of air separates off the back of the ball while in flight, and the location of that separation depends both on ball speed and on surface features. Buoyancy and chaotic swirling of air in the boundary layer’s wake are also ways in which the air influences a ball’s trajectory. A popular model takes the air to exert a single force on the ball, and that force is broken into three Cartesian components. Those components depend on the ball’s speed, v. Engineers usually prefer the use of Reynolds number over speed. The Reynolds number (Re) is defined as $\mathrm{Re}=vD/\nu$, where D = 0.22 m is a soccer ball’s diameter and $\nu =1.57\times {10}^{-5}{\mathrm{m}}^2/\mathrm{s}$ is the air’s kinematic viscosity at 29 °C [7]. Because $\mathrm{Re}\gg 1$ for essentially all speeds, a soccer ball would have, while in flight above the pitch, an inertial drag on a ball that completely dominates viscous drag [7]. The drag force, $F_D,$ on a soccer ball is thus modelled as [7]:

$$F_D=\frac{1}{2}{C}_D\rho A{v}^2,$$

(1)

where $\rho =1.2 \mathrm{kg}/{\mathrm{m}}^3$ is the density of air, $A=\pi D^2=0.038 {\mathrm{m}}^2$ is the cross-sectional area of a soccer ball, and $C_D$ is the dimensionless drag coefficient, which, for a soccer ball, depends on the ball’s speed and on the ball’s angular speed about its center of mass. The drag force points opposite to the ball’s velocity through air.

Ignoring the small buoyant force on a soccer ball, which is only about 1.5% of a ball’s weight, the other two components of the air’s force on a ball are the side force, $F_S,$ and the lift force,$F_L,$ which are modelled as [7]:

$$F_S=\frac{1}{2}{C}_S\rho A{v}^2$$

(2)

and [7]:

$$F_L=\frac{1}{2}{C}_L\rho A{v}^2,$$

(3)

where $C_S$ and $C_L$ are the dimensionless side coefficient and the dimensionless lift coefficient, respectively. Like the drag coefficient, the side and lift coefficients are functions of ball speed and ball angular speed. The side and lift forces arise from the same mechanism, namely an asymmetric shedding of the boundary layer of air off the back of the ball. The side force is perpendicular to the plane formed by the drag force and the ball’s weight. The lift force is in the plane formed by the drag force and the ball’s weight; the lift force is perpendicular to the drag force. A ball with pure topspin or backspin has essentially no side force, whereas a ball with pure sidespin has essentially no lift force. It is common to use the term Magnus force for the lift and side forces in the two aforementioned cases.

If one wishes to fundamentally understand how air acts on a soccer ball, and if one wishes to model the flight of a soccer ball through air, one must find the drag, side, and lift coefficients as functions of the center-of-mass translational speed and the angular speed about the center of mass. Those coefficients depend on the surface features of a soccer ball, such as the panel geometry, panel texturing (if any), and seam geometry. Because the size of the aerodynamic forces is intimately tied to the way in which the boundary layer of air separates from a soccer ball, a ball’s surface features not only influence how and where the boundary layer separates, but also the ball’s trajectory.

This paper’s authors have provided copious references to a myriad of strategies employed by researchers for determining the aerodynamic coefficients. Readers are referred to previous works [1,2,3,4,5,6] for those references. The authors of this work have used a wind tunnel as the primary tool for finding the aerodynamic coefficients.

2. Experimental Methods and Discussion

Figure 1 shows a soccer ball mounted on a support rod and placed in front of the wind tunnel at the University of Tsukuba (Japan). The open end of the wind tunnel has an area of 1.5 m × 1.5 m, which means only approximately 1.7% of that wind tunnel area was blocked. Regardless of the temperature at the time of any given test, all Reynolds numbers were scaled to 29 °C. Over the years in which tests were performed, temperature variations contributed less than 2% variation in the kinematic viscosity, so the results in this work are not strongly dependent on temperature fluctuations.

All tests on soccer balls were performed in the speed range 7 m/s $\le$ v $\le$ 35 m/s, which corresponds roughly to ${10}^5\le \mathrm{Re}\le 5\times {10}^5$. Data were obtained in 9-s time intervals using a six-component, sting-type balance (LMC-6522; Nissho Electric Works Co., Ltd., Tokyo, Japan) with a 1000 Hz sampling rate. For any given ball with a user-specified orientation, once forces were determined in the three Cartesian directions shown in Figure 1, Equations (1)–(3) were then used to extract the aerodynamic coefficients. Because wind speeds were varied in 1-m/s increments, a reasonably good determination of the aerodynamic coefficients’ dependences on speed were found. All tests were performed on balls without spin; testing balls with spin will be part of a future work.

This paper’s authors have reported wind tunnel results for nearly two dozen different soccer balls during the course of their collaboration [1,2,3,4,5,6]. Ball types have included those used in recent editions of the World Cup, match balls for professional leagues, inexpensive balls used by amateurs, and bespoke balls designed specifically to tease out the aerodynamic influence of a particular surface feature on a ball. 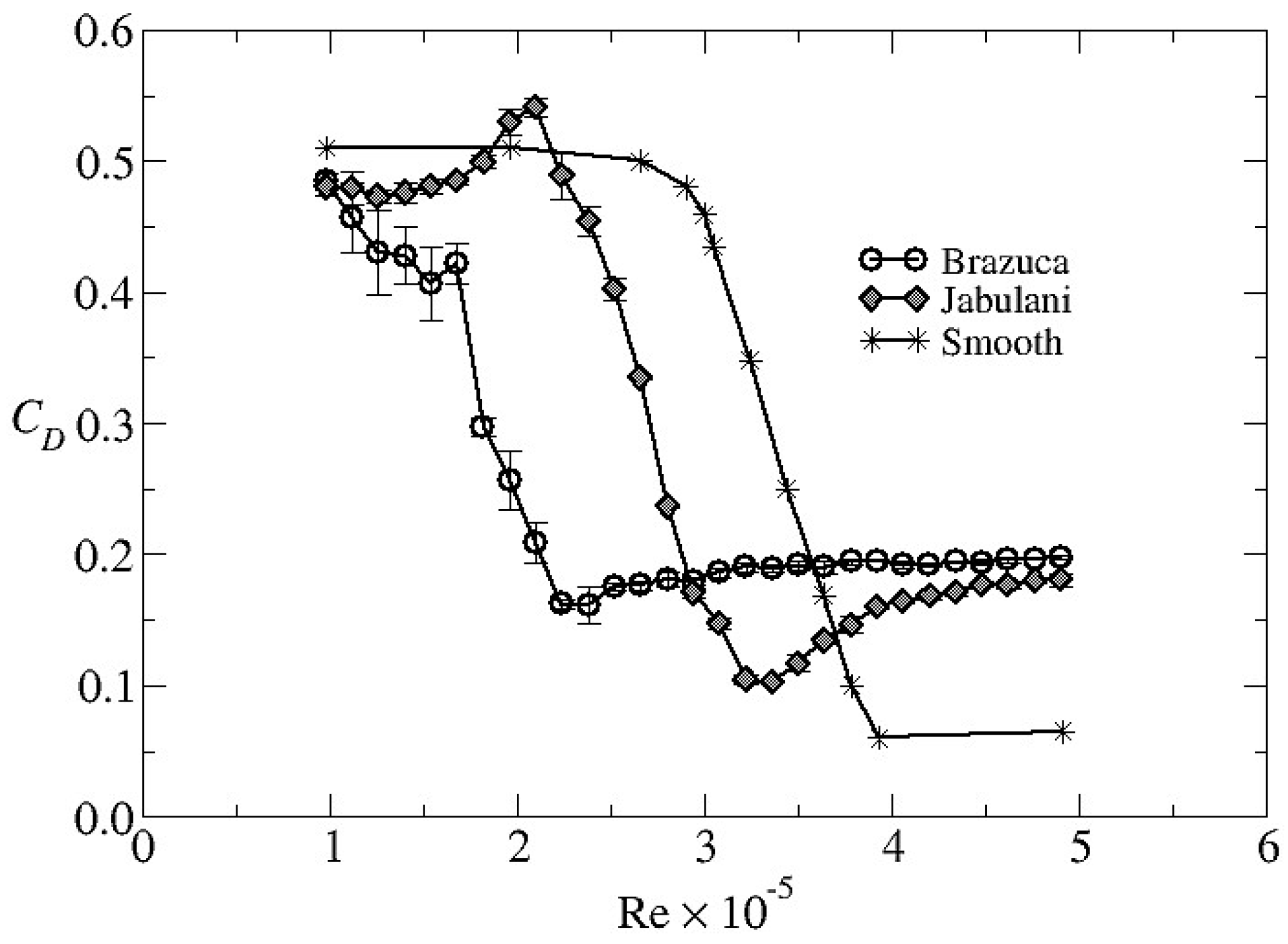Space limitations prevent us showing data from all balls tested, but Figure 2 does show typical drag coefficient data for two World Cup soccer balls (2010’s Jabulani and 2014’s Brazuca) [1] and a smooth ball of the same diameter as a soccer ball [8]. Experimental error bars are shown for the soccer ball data.

Much may be gleaned from Figure 2. The precipitous drop in the drag coefficient as the Reynolds number increases is called the drag crisis, and it represents a change in air flow around a ball. As the speed of air flow increases around a ball through the drag crisis, boundary layer separation changes from laminar flow to turbulent flow. A turbulent boundary layer of air separates farther back on a ball compared to the case of laminar flow. The critical Reynolds number corresponds to the Reynolds number at the minimum value of the drag coefficient, just after the precipitous drop. Note from Figure 2 that the smooth ball has the largest critical Reynolds number. It is well known that adding roughness to balls reduces their critical Reynolds number, which is why dimples and stitches help golf balls and baseballs, respectively, travel farther than if those balls were smooth. Similar results have been seen by many other researchers; see, for example, reference [9]. Note also from Figure 2 that Jabulani’s drag crisis occurred at a larger Reynolds number, and hence a larger speed, than it did for Brazuca. That partially explains why there were problems with Jabulani during the 2010 World Cup because the drag crisis occurred in the middle of the speed range for typical long kicks, free kicks, and corner kicks [1]. The improvement with Brazuca was a longer total seam length and coarser texturing, despite the fact that Brazuca had two fewer panels compared to Jabulani.

The observation about Jabulani made in the previous paragraph partially motivates this paper’s upcoming meta-analysis. Besides gaining a fundamental understanding of how air flow interacts with a surface, such as on a soccer ball, understanding how a soccer ball’s surface features, like seams, panel shapes, panel texturing, and total seam length, influence a ball’s trajectory is crucial if ball manufacturers are to produce new balls that have very similar aerodynamic properties to the balls players are accustomed to using.

3. Meta-Analysis

The focus of the following meta-analysis will be on the critical Reynolds number and how the various surface features of a soccer ball influence that number.

Table 1. Balls tested during several studies [1,2,3,4,5,6], each with their critical Reynolds number (Re_c), panel type (p is number of panels), total seam length, seam width, and seam depth.

Ball	${\mathit{Re}}_{\mathit{c}}\times {10}^{-5}$	Panel Type	Seam Length	Seam Width	Seam Depth
Ball A [4]	2.565	32p, textured	3850 mm	3.3 mm	1.0 mm
Ball B [4]	2.510	32p, textured	3850 mm	3.3 mm	1.0 mm
Ball C [4]	2.385	32p, textured	3850 mm	3.3 mm	1.0 mm
Ball D [4]	2.530	32p, textured	3850 mm	3.3 mm	1.0 mm
Ball E [4]	2.360	32p, textured	3850 mm	3.3 mm	1.0 mm
Brazuca [3]	2.325	6p, textured	3320 mm	4.0 mm	1.4 mm
Brazuca 32p [5]	2.745	32p, smooth	3850 mm	3.30 mm 1	1.05 mm 1
BrilliantSuper [6]	1.7	32p, smooth	3850 mm	5.0 mm	1.9 mm
Cafusa [6]	2.5	32p, textured	4470 mm	3.4 mm	1.1 mm
Conext15 [6]	2.4	6p, textured	3320 mm	8.0 mm	1.6 mm
Finale [6]	2.1	32p, textured	5100 mm	5.9 mm	1.4 mm
Jabulani [1]	3.4	8p, textured	1980 mm	2.2 mm	0.5 mm
Molten 4000 [5]	2.070	32p, smooth	3850 mm	5.88mm 1	1.73 mm 1
Molten 5000 [5]	2.070	32p, smooth	3850 mm	4.98 mm 1	1.30 mm 1
Pelada I [6]	2.2	32p, smooth	3850 mm	5.7 mm	1.7 mm
Pelada II [6]	1.8	32p, smooth	3850 mm	4.0 mm	1.0 mm
Select R [5]	1.780	32p, smooth	3850 mm	6.84 mm 1	1.53 mm 1
SelectNumero [5]	2.190	32p, smooth	3850 mm	4.70 mm 1	1.45 mm 1
Teamgeist2 [6]	3.0	14p, textured	3470 mm	2.3 mm	0.7 mm
Telstar 18 [3]	2.475	6p, textured	4320 mm	3.3 mm	1.1 mm
Vantaggio [6]	2.5	32p, smooth	3850 mm	6.8 mm	1.8 mm

¹ Reference [5] contains an error. The words “depth” and “width” must be switched throughout.

organizes soccer ball data from several studies [1,2,3,4,5,6] undertaken by the authors of this paper. The 21 entries are alphabetized by ball name. Balls listed for studies [3,4,5] have critical Reynolds numbers that are averaged over the orientations tested.

Because soccer balls are not perfectly symmetrical, values of aerodynamic coefficients change when ball orientation is changed in the wind tunnel. Rotating balls 90° about the support rod from one test to the next causes side and lift coefficients to essentially swap magnitudes. Such rotations may lead to changes of 10% in the critical Reynolds number. The challenge facing a meta-analysis of the data in Table 1 is the large number of parameters on which the critical Reynolds number may depend, and space limitations in Table 1 and in this paper do not allow for a full description of all such parameters. There are an infinite number of wind tunnel ball orientations from which a researcher can choose, and each new test that requires any rotation other than a rotation about the support rod requires a new soccer ball. The insertion of a support rod destroys a ball for use other than wind tunnel testing and surface inspection. There are a myriad of surface textures. Balls listed in Table 1 with the “Ball” label were bespoke balls for a study [4] that attempted to keep all features of a 32-panel soccer ball the same, except for the surface texturing. For all the various types of panel textures, balls vary by their panel number, total seam length, seam width, seam depth, and the way in which panels are joined, be they stitched together or thermally bonded. Teasing out the one surface property that influences the critical Reynolds number more than any other ideally requires an experimenter to use a selection of balls that have just one surface property that is different among them. The question of ball orientation in the wind tunnel then arises. Testing multiple orientations requires the use and destruction of many soccer balls. Even if experimenters could test a wide variety of orientations for each of at least half a dozen studies that try to isolate one surface parameter, the meta-analysis could still miss multi-way interactions, and searching for multi-way interactions could require a large data set.

Given all the aforementioned caveats, a meta-analysis may still be performed on the information contained in Table 1. A full analysis of variance on the data contained in Table 1 shows that the critical Reynolds number is influenced more by texturing and seam width than by total seam length and seam depth. The former two parameters give $p<{10}^{-2}$, whereas the latter two parameters give $p>{10}^{-2}$. The fact that increasing surface roughness on a ball reduces its critical Reynolds number has been known for some time [10]. The meta-analysis here and the results of previous work [5,6] reveal a correlation between critical Reynolds number and seam width, such that increasing seam width lowers the critical Reynolds number. Increasing total seam length, texturing panels, and widening seams all contribute to the roughening of a soccer ball, but seam width appears to have the largest effect on a ball’s critical Reynolds number. More investigation is needed to determine exactly how panel texturing alters the critical Reynolds number, as well as if there is a critical width at which increasing seam width beyond a critical value will no longer change the critical Reynolds number.

4. Surface Influences on Ball Trajectory

All previous relevant work published by this paper’s research collaboration [1,2,3,4,5,6] has calculated simulated no-spin trajectories for the entire speed range used by the wind tunnel, and a portion of that previously published work will be synthesized here. Solving Newton’s second law equation numerically for a kicked ball that experiences forces described by Equations (1)–(3), as well as the ball’s weight, is fully described elsewhere [11].

Consider a soccer ball kicked at the maximum air speed the wind tunnel can produce, which is 35 m/s. Such a launch speed would be appropriate for a long free kick or a corner kick. For a launch angle of 25°, all balls listed in Table 1 would travel a horizontal distance in the range 60 m–70 m. For an average range of approximately 65 m, the surface influences on trajectories for the 21 balls listed in Table 1 means that ±8% of the average range is needed to cover all simulated ranges. About half that percentage represents the standard deviation in horizontal ranges. A ball kicked with a launch speed of 35 m/s at 25° above the horizontal travels about 96 m in a vacuum. Turning on air drag knocks 32% off the vacuum horizontal range. A ball’s surface features do not influence the ball’s trajectory nearly as much as the drag itself, but altering those surface features will produce noticeable changes in the ball’s horizontal range.

Side and lift coefficients are much closer to zero for speeds larger than the critical speed than they are for speeds smaller than the critical speed [1,2,3,4,5,6]. However, the fact that the side and lift coefficients are not zero for non-spinning, high-speed kicks means that those coefficients affect both a ball’s horizontal range and its lateral deflection. Turning off the lift coefficient for the 35 m/s kick at 25° above the horizontal alters the horizontal range by 0%–30%, with Ball A in Table 1 representing the 30% change. A nonzero lift coefficient caused by an asymmetric shedding of the boundary layer, influenced by a ball’s surface properties, may cause a ball’s horizontal range to vary by more than the influences those surface properties have on the ball’s drag coefficient. Nonzero side coefficients may cause lateral deflections as large as 20% of the ball’s horizontal range, though the balls in Table 1 that are responsible for such a large percentage are the bespoke balls of reference [4]. Normal league and World Cup soccer balls from Table 1 will see lateral deflections no larger than about 10% of the horizontal range when kicked 35 m/s at 25° above the horizontal.

The fact that a hard-kicked ball that might be expected to travel 65 m could have its horizontal range altered by ±4 m and be laterally deflected by ±4 m, both because of changes made to the ball’s surface, means that elite soccer players will surely notice such alterations in ball trajectory. Soccer ball manufactures will be wise to ensure that the new balls they produce, which will likely possess surface features different from older balls, have aerodynamic properties similar to the balls soccer players have already used. That means that new balls should have critical Reynolds numbers similar to older balls, which was not done for Jabulani, and that the changes in ball surface will not alter post-critical aerodynamic coefficients too much. The authors of this paper hope that the work presented here and in previous studies [1,2,3,4,5,6] will help soccer ball manufacturers better understand how various surface features influence a soccer ball’s trajectory.

5. Conclusions

Several soccer balls were tested in a wind tunnel over a range of air speeds that are congruent with ball speeds in actual soccer matches. After finding the critical Reynolds number for each soccer ball, it was determined that the critical Reynolds number is more strongly correlated with a ball’s seam width than with its seam depth. This information should aid ball manufacturers in designing new balls that possess aerodynamic properties similar to the balls players are accustomed to using. The authors of this work plan to test more balls in the future with the goal of determining the robustness of this paper’s conclusion.