Standard of the Initial Ball Velocity for a Fly Ball in Baseball Hitting ^†

Abstract

This study aimed to determine the minimum required initial velocity to hit a fly ball toward the same field (left-field for right-handed batters), center field, and opposite field (right field for right-handed batters). Six baseball players hit fastballs launched by a pitching machine. The movements of the balls before and after bat-to-ball impact were recorded using two high-speed video cameras. The flight distance was determined using a measuring tape. Seventy-nine trials were analyzed, and the minimum required initial velocities of batted balls were quantified to hit balls 60, 70, 80, 90, 100, 110, and 120 m in each direction through regression analysis. As a result, to hit a ball 120 m, initial velocities of 43.0, 43.9, and 46.0 m/s were required for the same field, center field, and opposite field, respectively. The result provides a useful index for batters to hit a fly ball in each of the directions.

1. Introduction

To win baseball games, batters on one team are required to score more points than the opposing team. Statistics in baseball are well established and reveal vital information, one of which is called a team’s slugging percentage. This percentage evaluates the team’s batting performance and takes into consideration extra base hits, including home runs, and correlates those numbers with those of the team’s scored runs. Thus, hitting a fly ball is one of the most important skills in baseball.

The most important factor influencing the flight distance of a batted ball is its initial velocity. To increase the initial velocity of a batted ball, batters must increase the velocity with which they swing their bat. To that end, there has been a great deal of discussion about how to increase the bat swing velocity [1,2]. On the other hand, not only the initial velocity but also the launch angle and the batted ball’s spin can affect the flight distance. Previous research reported that the maximum distance is obtained with balls hit at a launch angle of about 35° from a horizontal plane [3] (pp. 16–22). Other research that investigated the effect of spin on the flight distance reported that, as the backspin of a batted ball increased, the flight distance also increased for a given initial velocity and launch angle [4]. It was calculated that the flight distances of batted balls were a result of initial velocity when hitting a ball at a launch angle of 35° and a backspin rate of 2000 rpm [3]. Batters dedicate time to improve their bat swing velocity, initial velocity of batted balls, and flight distance. Thus, the flight distance estimated from the initial velocity of the batted ball [3] is a useful index to help batters hit a fly ball.

However, the study mentioned above [3] did not consider the effect of sidespin. In [5], researchers investigated the three-dimensional movement of batted balls, including their sidespin, and compared their characteristics when the balls were hit towards the same field (left field for right-handed batters), center field, and opposite field (right field for right-handed batters). As a result, although the initial velocities of the batted balls did not differ regardless of the direction, sidespin for balls hit towards the opposite field were greater than those for the other fields. In addition, these batted balls were curved horizontally during their flights because of the Magnus effect, and their flight distances tended to be shorter. In this manner, regardless of the same initial velocity, the flight distances were different depending on the direction in which the ball was hit. It would be useful for batters to understand what is required of the initial velocity to hit a fly ball in each direction, because batters need to hit a ball in varying directions, depending on the situation. With this in mind, batters should be able to train more efficiently while pursuing these goals.

The purpose of this study was to determine the minimum required initial velocity of batted balls in order to hit them a long distance toward the same field, center field, and opposite field.

2. Methods

2.1. Participants

Six collegiate male baseball players (age: 20.5 ± 0.3 years, body height: 1.78 ± 0.02 m, and bodyweight: 75.7 ± 3.7 kg) participated in this study. All the participants were right-handed batters. The ethics committee of Chukyo University approved the study protocols. Before conducting the experiment, the participants were apprised of the purpose of the study and experimental protocols. Written informed consent was obtained from each participant.

2.2. Procedure

The experiments were conducted in an outdoor baseball field (left and right field: 91.4 m, and center field: 120 m). After a sufficient warm up, the participants were asked to hit fastballs launched by a two-wheel ball pitching machine. The batters were instructed to hit the ball as far as possible. For the completion of a successful trial, the following two prerequisites were established: (1) the batted ball must land in fair territory; (2) the flight distance must be more than 60 m. The experiment was repeated until at least five successful trials were recorded in all three directions of fair territories. As shown in Figure 1, the fair territories were divided into three sections (i.e., same field, center field, and opposite field for 30$°$ each). The pitching machine was placed approximately 1.5 m in front of the pitcher’s rubber. The mean pitched ball velocity during the experiment was 24.0 ± 1.5 m/s. A wooden bat (1CJWH11184; length = 0.84 m; mass = 0.90 kg; Mizuno, Japan) and official Japan amateur league baseballs (2CH11000; Mizuno, Japan) were used.

2.3. Data Collection

The movements of the balls before and after the bat-ball impact were recorded using two high-speed video cameras (Phantom Miro, Vision Research, Wayne, NJ, USA) with a frame rate of 500 fps and an exposure time of 1/20,000 s. The placement of these cameras is illustrated in Figure 1. To construct the three-dimensional space around the batters, a 2.4-m pole with seven equally spaced markers was erected vertically at six places and photographed successively. The flight distance was determined using a measuring tape; the straight-line distance from the tip of the home plate to the landing points was regarded as the flight distance. A theodolite was used to identify the landing points of the batted balls. To consider the effect of the wind on the flight distance, the wind velocity was measured for each trial. Camera calibration was conducted before the experiment.

2.4. Data Analysis

Any trials, for which the wind velocity was more than 1.5 m/s and the landing points could not be identified (such as home runs), were eliminated from the study, and 79 trials (same field: 24 trials, center field: 29 trials, and opposite field: 26 trials) were analyzed. The three-dimensional coordinates of the center of the balls were obtained using the direct linear transformation method with video motion analysis software (Frame DIAS V, DKH Co., Nerima-ku, Japan). 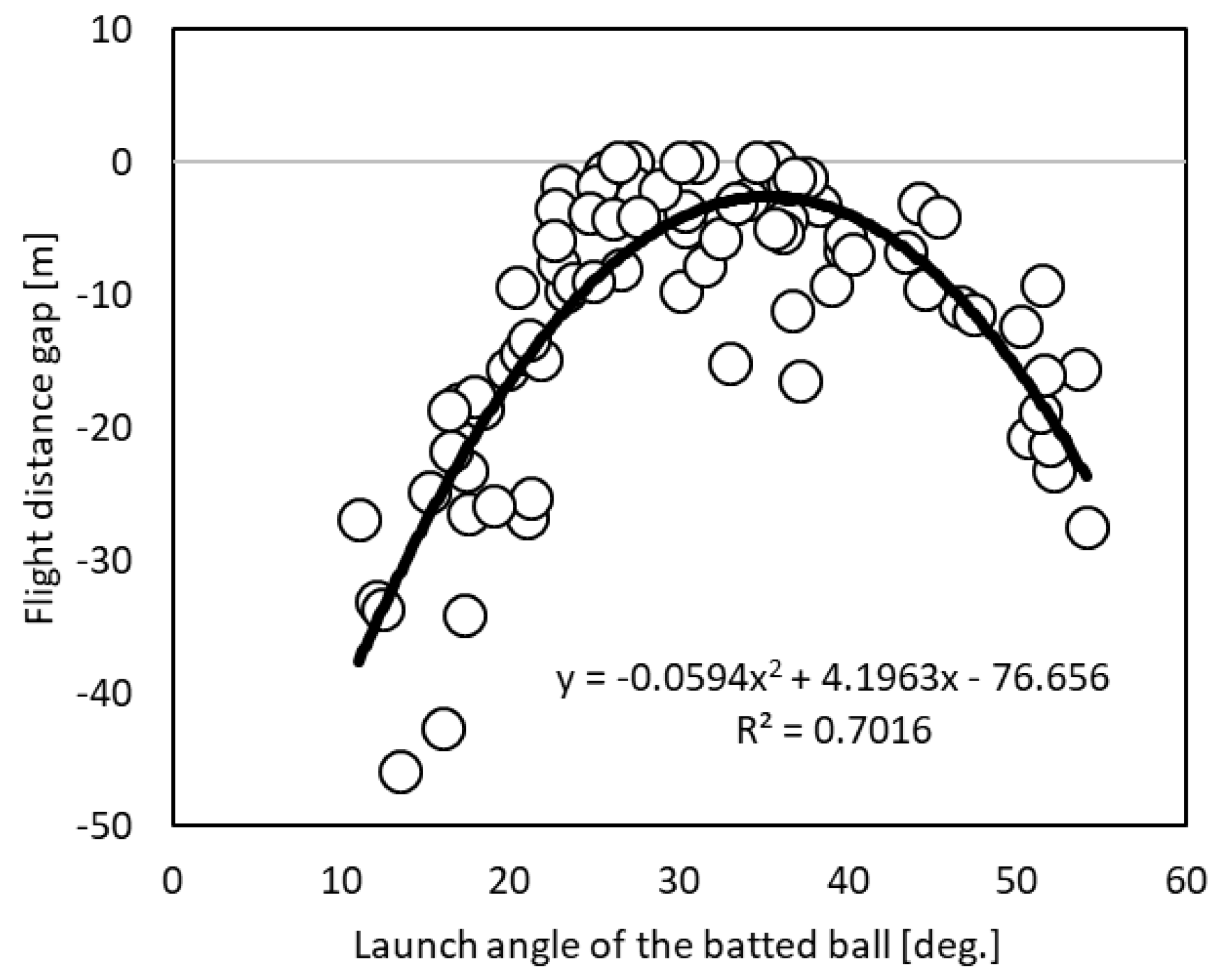The global coordination system was constructed by using Y as the horizontal direction from the home plate to the pitcher’s plate, Z as the vertical direction upward, and X as the cross product of Y and Z (Figure 1). The pitched ball velocity and the initial velocity of the batted balls were calculated based on the displacements of the coordinate immediately before and after the bat-ball impact, respectively. Three linear functions, which estimated the flight distance from the initial velocity of the batted ball for each batted ball direction, were obtained under two conditions: (1) the measured values did not exceed the predictive values and (2) the residual sum of squares between the linear function and the measured values was minimized. In brief, the top edge lines of the flight distance were acquired for each direction by considering the initial velocity and flight distance of the batted balls as the horizontal and vertical axes, respectively. The upper limit of the flight distance expected by a certain batted ball velocity was determined. Additionally, the minimum required initial velocities of batted balls were quantified to hit a ball 60, 70, 80, 90, 100, 110, and 120 m long for each direction. Further, the launch angle of the batted ball, which is the angle between the initial velocity vector of the batted ball and the horizontal plane, was calculated. To determine the appropriate launch angle to hit a fly ball, we carried out the following analysis. First, the flight distance gap, which is the measured flight distance minus the maximum flight distance expected from the initial velocity using the above-mentioned regression lines, was calculated. Then, the relationship between the launch angle and the flight distance gap was investigated.

3. Results

The ranges of flight distance for the same field, center field, and opposite field were 62.2–109.2, 61.2–119.0, and 64.4–96.3 m, respectively. Figure 2 shows the relationship between the initial velocity of batted balls and the flight distance. The lines show the maximum flight distance as a function of the initial velocity of the batted ball for each direction (same field: y = 3.51x − 30.89, center field: y = 3.38x − 28.32, and opposite field: y = 3.19x − 26.78).

Table 1. Minimum required initial velocity of batted ball for hitting a fly ball.

	Same-Field	Center-Field	Opposite-Field
60 m	25.9 m/s	26.1 m/s	27.2 m/s
70 m	28.8 m/s	29.1 m/s	30.4 m/s
80 m	31.6 m/s	32.1 m/s	33.5 m/s
90 m	34.5 m/s	35.0 m/s	36.6 m/s
100 m	37.3 m/s	38.0 m/s	39.8 m/s
110 m	40.2 m/s	40.9 m/s	42.9 m/s
120 m	43.0 m/s	43.9 m/s	46.0 m/s

shows the minimum initial velocities of a batted ball needed to hit a ball 60, 70, 80, 90, 100, 110, and 120 m toward the same field, center field, and opposite field. In Figure 3, the relationship between the launch angle of the batted ball and the flight distance gap is shown.

4. Discussion

In this study, we determined the initial velocity of a batted ball necessary to hit the ball a certain distance toward the same field, center field, and opposite field. Moreover, it was confirmed that a higher initial velocity for the batted ball was required to hit a fly ball toward the opposite field compared to the other fields. For example, to hit a ball 120-m long, an initial velocity of 46.0 m/s was required, whereas only 43.0 m/s was needed to reach that distance for the same field, and 43.9 m/s for the center field was required.

Further, we identified that the batted balls with a launch angle of approximately 20–40$°$ fly farther for their initial velocity. Therefore, it can be inferred that the batters should give the balls a launch angle of 20–40$°$ along with imparting the above-mentioned velocity to hit a fly ball.

In the previous study [6], the relationship between the velocity of the distal end of the bat (bat swing velocity) and initial velocity of the batted ball was investigated using high-speed video cameras. It also quantified the maximum initial velocity of the batted ball expected from a certain bat swing velocity using regression analysis. Specifically, a linear function, which estimates the initial velocity of the batted ball from the bat swing velocity, was obtained under two conditions: (1) the measured value of initial velocity of batted ball did not exceed the predictive values and (2) the residual sum of squares between the linear function and the measured values was minimized. As a result, it could be represented by a linear function, y = 0.872x + 12.984 where y is the initial velocity of the batted ball and x is the bat swing velocity. This equation was considered to be applied when batters could hit a ball with a sweet spot and its ball resulted in a line drive. Because the relationship between the bat swing velocity and initial velocity of batted balls is influenced by the pitched ball velocity and materials of the bat [7], it was difficult to determine the minimum required bat swing velocity to hit a fly ball. Despite these limitations, while applying the results of the present study to this equation, to hit a ball 120 m, the bat swing velocities of 34.4 m/s for the same field, 35.5 m/s for the center field, and 37.9 m/s for the opposite field were required. While considering that batters must impart not only high velocity but also an appropriate launch angle and backspin to the ball, batters must increase their bat head velocity to at least more than the above-mentioned velocity to hit a ball 120 m.

In recent years, sensors have been developed, which easily measure the initial velocity of a batted ball and the bat swing velocity, and players can measure their performance and understand their states. The result of the present study would be helpful for batters to understand how far they can hit a ball and would be a useful index to measure their progress to concrete goals.

This study had two limitations. First, trials for which a landing point could not be measured (such as home runs) were eliminated. Hence, it was considered that the relationship between the flight distance and the initial velocity of batted balls was partly extrapolated, and the flight distance as a function of the initial velocity of batted balls might be underestimated. However, initial velocities of batted balls in home runs trials were the highest in trials hit in the corresponding direction. In the case of the trials of home runs, they would be distributed on an extension of regression lines in Figure 2. Therefore, it was considered that the effect of the eliminated trials on the result of the present study was relatively small. Second, we could not include the effect of the spin of the batted balls. The flight distance was influenced not only by the velocity and the launch angle but also the spin of the batted ball, and we should account for it in our future work.

5. Conclusions

This study determined that the minimum required initial velocities to hit a ball a long distance toward the same field, center field, and opposite field. This provides a useful index for batters to hit a fly ball.