Abstract
An on-site Ring of Fire (RoF) experiment is performed at the Tom Dumoulin bike park in Sittard-Geleen, the Netherlands. The current work investigates the aerodynamic drag of a cyclist following a lead cyclist at different lateral and longitudinal separations; additionally, the athletes’ skills to maintain their position and distance with respect to the preceding riders are evaluated. The effect of the relative size of the lead cyclist on the drag area of the drafting cyclist is also investigated. The results show drag reductions of the trailing cyclist in the range from 27% to 66% depending on the longitudinal and lateral separation from the leading rider. The aerodynamic advantage of the drafting rider decreases with increasing lateral and longitudinal separation between riders, with the lateral separation found to be more relevant. Besides this, the drag reduction of the drafting cyclist benefits from an increase in drag area of the leading cyclist.
1. Introduction
At cycling velocities beyond 15 km/h, the aerodynamic drag of an individual rider becomes the dominant resistance. In these conditions, more than 90% of the athlete’s power is expended to overcome the air resistance [1]. Most research on cycling aerodynamics has been carried out by force balance measurements to quantify the aerodynamic drag of individual riders for different riders’ positions or equipment [2]. More recently, some studies have been reported which investigated the flow mechanisms responsible for the aerodynamic drag [3]. However, in most race events, athletes ride in close proximity to each other, thus benefitting from a significant reduction in aerodynamic drag [4]. Some examples of multiple rider events include the team time trial in road cycling and the team pursuit and team sprint in track cycling. In these events, the effect of drafting on the aerodynamic drag is a key element in the pacing strategy, since drag optimization of each cyclist individual does not lead per se to the lowest drag for the group. The aerodynamic optimization of such a group must take into account three important elements: the spatial position of the riders, i.e., the longitudinal (in travelling direction) and sideways separations among riders [5,6]; the inter-individual size differences [7]; and finally, the athletes’ skills, and in particular how well the athletes are able to maintain their position and distance with respect to the preceding riders [8]. Currently, none of the state-of-the art techniques for investigating cycling aerodynamics (wind tunnel, Computational Fluid Dynamics and track measurements) is able to measure the effect of these three elements simultaneously nor optimize for them.
In the recent years, a measurement concept has been introduced by the authors, named the Ring of Fire (RoF) ([9]). The concept is based on large-scale stereoscopic particle image velocimetry (PIV) measurements in quiescent air where an object or a vehicle travels through it. The analysis of the momentum difference between the conditions prior to and after the passage poses the basis to estimate the aerodynamic drag. The measurement system was shown to provide the aerodynamic drag of an individual cyclist during sport action and returned a quantitative visualization of the flow field in the wake [9]. Thanks to the ability to measure the flow field in the wake of a cyclist, as well as the posture and the relative distances between riders, the Ring of Fire system is in principle suitable for the investigation of the aerodynamics of a group of riders. For this reason, the Ring of Fire system is deployed to evaluate the effects of cyclists’ position and their relative size on the aerodynamic drag.
2. Methodology
The drag evaluation through the Ring of Fire follows those of previous investigations [9]. The instantaneous drag force D(t) is evaluated by invoking the conservation of momentum expressed in a control volume around a cyclist. The cyclists are assumed to move at constant speed with respect to the laboratory frame of reference. In case of an individual cyclist, the air motion prior to the passage features a chaotic velocity , resulting from the environmental effects. After the passage, the flow velocity features a coherent wake with a velocity field that follows the moving cyclist. The drag of a group can be determined in a similar way by invoking the conservation of momentum across surfaces S1 (in front of lead cyclist) and S3 (behind drafting cyclist). The velocity and momentum changes can be written in the cyclist’s frame of reference, enabling the derivation of the following expression for the instantaneous drag of the entire group:
where is the air density. This expression is valid at the condition that the mass flow is conserved across surfaces S1 and S3. The drag of the individual cyclists within the group can be calculated in the same way, namely by enforcing the conservation of momentum across surfaces S1 and S2 for the leading cyclist, and across surfaces S2 and S3 for the drafting cyclist.
In order to achieve a higher degree of statistical convergence, an ensemble average of the drag among multiple passages is performed, followed by a time average in order to reduce the effect of the unsteady fluctuations:
where T is the total number of time instants composing the measurement and N is the number of model passages.
3. Experimental Setup and Procedures
The measurements were conducted at the Tom Dumoulin bike park of Sittard-Geleen in the Netherlands. The facility is built on a 6-hectare area and contains a total of 3.2 km track. Numerous courses are present that vary in difficulty with different surface types, differences in altitude, and challenging turns. The experiment was conducted on the 1.1 km, flat, oval outer lap. Six male subjects were recruited from the development team of the cycling team Sunweb. Subjects were required to perform a series of individual tests as well as six different drafting tests, throughout which the sequence of the athletes was varied. Figure 1 shows one such passage of a drafting group through the RoF. All tests were performed at nominal riding speed of 45 km/h; when drafting, the riders were asked to maintain a wheel-to-wheel spacing of 0.3 m and to stay in-line with the lead rider. In practice, the longitudinal and lateral separations of the drafters varied respectively between 0.35 m and 0.85 m and between ±0.20 m among different runs. Subjects were required to wear the same clothing and to use the same equipment during all testing sessions. In addition to the skin suit and helmet, the riders wore laser safety goggles that absorb the wavelengths of the light emitted by the PIV laser unit. For each measurement configuration, a minimum of 10 trials were performed. For all trials, subjects started pedaling 300 m before the measurement region, accelerated to the prescribed velocity of 45 km/h and maintained such velocity up to about 100 m after the measurement region, where they ceased pedaling. Subjects were also required to maintain a constant racing posture (time-trial posture) within and across all trials. The faulty trials, i.e., those with too little tracer particles in the recorded images, were removed in the data post-processing phase.

Figure 1.
Picture of a drafting configuration passing through the Ring of Fire.
A detailed top view of the experimental setup is given in Figure 2. Velocity data upstream and in the wake of the cyclists were collected by means of a large-scale stereoscopic-PIV system. Neutrally buoyant helium-filled soap bubbles (HFSB) with an average diameter between 0.3 and 0.4 mm were used as flow tracers [10], providing sufficient light scattering to visualize a field of view (FOV) of the order of 4 m2. A tunnel of 8 × 5 × 3 m3 in x, y and z direction (see Figure 1) was used to confine the bubbles near the measurement plane. The tunnel had an open in- and outlet to allow the rider to transit and was equipped with optical access on one side for illumination purposes. The tracers were introduced in the measurement region by a rake with 200 nozzles positioned 1 m upstream of the measurement plane, adjacent to the tunnel side wall. The light source was a Quantronix Darwin Duo Nd:YAG laser emitting a green light with a wavelength of 532 nm with a maximum pulse energy of 25 mJ at a repetition rate of 1kHz. The laser beam was shaped into a 50 mm thick sheet by means of laser optics and light stops. The field of view was imaged by two Photron Fast CAM SA1 cameras (CMOS, 1024 × 1024 pixels, pixel pitch of 20 μm, 12 bits) equipped with 35 mm objectives at f/2.8. Images were acquired at 0.5 kHz and 1 kHz for the individual and drafting measurements, respectively. The pair of cameras was placed 4 m upstream of the measurement plane in an angular-displacement stereo configuration, at a full stereoscopic viewing angle of 2θ = 95 degrees. The resultant field of view captured by both cameras is 1.8 × 1.8 m2, yielding a magnification factor of 0.011 and a digital image resolution of 0.57 px/mm.
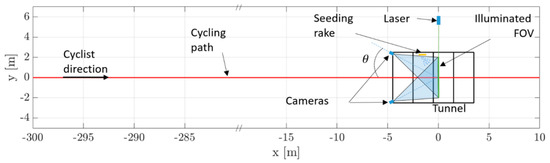
Figure 2.
Detailed top view of the experimental setup.
To maximize the concentration of tracers particles in the measurement domain, the entrance and exit gates of the tunnel were closed before the passage of the cyclist to enable the accumulation of the HFSB seeding for about two minutes. In order to maintain a sufficient seeding density, HFSB production remained running during data acquisition. When the cyclist was approximately 100 m before the entrance of the tunnel, entrance and exit gates were opened and data acquisition was started. The velocity of the cyclist as well as the drafting distance between riders was determined from the PIV recordings with an uncertainty of 0.1 m/s and 2 cm, respectively. The recorded images were processed with the LaVision DaVis 8.4 software by means of a cross-correlation based interrogation algorithm with image deformation, with final interrogation window size of 24 × 24 pixels and 75% overlap factor.
4. Results
This section only discusses the findings of the drafting configurations with two cyclists, although the three-rider group was also investigated. Table 1 summarizes the anthropometric characteristics of the subjects participating in these configurations as well as their individual drag area (CdA). The subjects are categorized from small (S1) to large (L1) in conformity with their height. Based on Equations (1) and (2), and on the procedures described in Section 2, the ensemble average drag area is computed for each cyclist individually. For every passage of the cyclists, only the first meter in the wake is considered for drag calculation. Based on the evolution of the measured drag area along the wake, it is concluded that the windy conditions in the outdoor test facility cause the drag measurements to become unreliable when flow measurements are conducted later than 0.1 s after the passage of the trailing rider. Furthermore, the rider transited the laser sheet with no predefined crank-angle, meaning that the crank-angle at the laser sheet location varied from run to run. The uncertainties of the drag area measurements are similar to those reported for previous RoF experiments, namely below 5% [9].

Table 1.
Subjects’ anthropometric characteristics and individual drag area (m2).
The drag of the drafting cyclist varies significantly as a function of his position with respect to the lead cyclist (see Figure 3 below). This is consistent with the existing literature for other experiments and simulations concerning aerodynamic interactions between multiple cyclist [4,5]. Figure 3a presents the drag savings of the second cyclist for different spatial positions behind the lead cyclist. The grid gives an indication of the separation between the rear wheel of the leading cyclist and the front wheel of the trailing cyclist at the moment they passed through the tunnel.
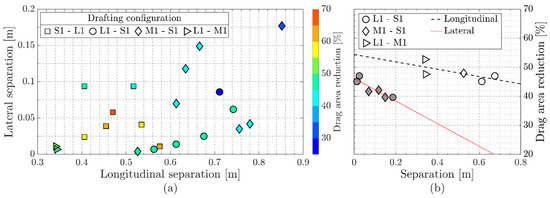
Figure 3.
(a) Reduction in drag area for the drafting cyclist at different positions behind the lead cyclist. (b) Effect of longitudinal and lateral separations on the drag reduction of the trailing cyclist. The filled symbols correspond to varying lateral separation with a longitudinal distance of 0.65 m ± 0.04 m. The empty symbols correspond varying longitudinal separation with a lateral separation of 0 m ± 0.02 m.
Except for the drafting configuration S1–L1, the magnitude of drag savings for the cyclists at the different locations is comparable to the work of Barry et al. (2014) [5]. For no lateral separation, the drag saving of the trailing rider is around 50–55% when he trails by 0.3 m, and it decreases to 45% at 0.7 m separation distance. At this latter longitudinal separation, the drag reduction is lowered to almost 35% when a 0.15 m lateral offset between the riders is present, again in agreement to the findings of Barry et al. (2014) [5]. Figure 3b indicates that the change in drag reduction is more related to the lateral displacement from the centerline than the axial separation distance. The figure shows the effect of longitudinal and lateral distances on drag reduction of the trailing cyclist. The effect of longitudinal distance is investigated at zero lateral distance and the effect of lateral distance is investigated at 0.65 m longitudinal separation. The comparison of the slopes shows that a decrease in longitudinal drafting distance of 10 cm translates to an increase in drag benefit by 1.3%, while a similar decrease in lateral distance translates to 3.9% increase in drag benefit. This shows that the lateral distance is approximately three times more important than the longitudinal distance. The configuration S1–L1 seems to follow the same trend: the drag reduction shows higher dependency on the lateral separation than on the longitudinal one; however, the drag reductions are significantly higher than the ones found by Barry et al. (2014) [5], up to 66%. This is attributed to the larger drag area (0.211 m2) of the leading cyclist; however, further analysis of the flow field interactions is needed to confirm this statement.
Edwards and Byrnes (2007) [11] hypothesized that the inter-individual variability between drafting cyclists is dependent on the drafter’s skill in positioning him- or herself within the leader’s wake because they did not see any correlation between the drafter‘s drag area reduction and anthropometric characteristics.
As mentioned in Section 3, at the start of the experiment all subjects received the same instructions, namely to maintain a constant longitudinal drafting distance of 0.3 m with zero lateral offset. A first look at Figure 3 shows a large variation in drafting distances between different runs from the same configuration as well as between different configurations. The average and standard deviation of drafting distances maintained by each cyclist while trailing another cyclist are obtained from 10 runs and are presented in Table 2.

Table 2.
Mean longitudinal and lateral separations for each cyclist in trailing position and the corresponding standard deviation obtained from 10 runs.
On average, it is noticed that the medium cyclist performed best in following the instructions, while the small cyclist has an average longitudinal drafting distance that is more than double the requested separation. Furthermore, in terms of the lateral separation, the small cyclist is outperformed by the other cyclists. Thus, ranking the three subjects from skilled to less skilled in drafting, subject M1 is the most skilled and S1 the least.
5. Conclusions
Time resolved stereo-PIV measurements are conducted to determine the drafting effect on cyclists when they ride behind a lead cyclist. The conservation of momentum in a control volume is adapted from [9] to determine the individual athletes’ aerodynamic drag. Within the measured spectrum, the savings for the drafting cyclist range from 27% to 66%. The aerodynamic advantage decreases as lateral and longitudinal separation between riders is increased, where the lateral distance is found to be more relevant. Furthermore, it is observed that the larger the isolated drag area of the leading cyclist is, the larger the benefit for the drafting cyclist. Besides these results, the RoF also shows great potential to simultaneously give an indication of the drafting skill level of cyclists, which is infeasible with the current state-of-the-art measurement techniques for cycling aerodynamics.
Funding
This research was funded by the Netherlands Organisation for Scientific Research (NOW) Domain Applied and Engineering Sciences (TTW), project 15583 “Enabling on-site sport aerodynamics with the Ring of Fire”.
Acknowledgments
The support of Team Sunweb who provided the cycling equipment and cyclists for the experiment is kindly acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lukes, R.A.; Chin, S.B.; Haake, S.J. The understanding and development of cycling aerodynamics. Sports Eng. 2005, 8, 59–74. [Google Scholar] [CrossRef]
- Garcia-Lopez, J.; Rodriguez-Marroyo, J.; Juneau, E.; Peleteiro, J.; Martínez, A.; Villa, J. Reference values and improvement of aerodynamic drag in professional cyclists. J. Sports Sci. 2008, 26, 277–286. [Google Scholar] [CrossRef] [PubMed]
- Crouch, T.N.; Burton, D.; Brown, N.A.T.; Thompson, M.C.; Sheridan, J. Flow topology in the wake of a cyclist and its effect on aerodynamic drag. J. Fluid Mech. 2014, 748, 5–35. [Google Scholar] [CrossRef]
- Blocken, B.; Toparlar, Y.; van Druenen, T.; Andrianne, T. Aerodynamic drag in cycling team time trials. J. Wind Eng. Ind. Aerodyn. 2018, 182, 128–145. [Google Scholar] [CrossRef]
- Barry, N.; Sheridan, J.; Burton, D.; Brown, N.A.T. The effect of spatial position on the aerodynamic interactions between cyclists. Procedia Eng. 2014, 72, 774–779. [Google Scholar] [CrossRef]
- Belloli, M.; Giappino, S.; Robustelli, F.; Somaschini, C. Drafting effect in cycling: Investigation by wind tunnel tests. Procedia Eng. 2016, 147, 38–43. [Google Scholar] [CrossRef]
- Fitton, B.; Caddy, O.; Symons, D. The impact of relative athlete characteristics on the drag reductions caused by drafting when cycling in a velodrome. Proc. Inst. Mech. Eng. Part P J. Sports Eng. Technol. 2018, 232, 39–49. [Google Scholar] [CrossRef]
- Broker, J.P.; Kyle, C.R.; Burke, E.R. Racing cyclist power requirements in the 4000-m individual and team pursuits. Med. Sci. Sports Exerc. 1999, 31, 1677–1685. [Google Scholar] [CrossRef] [PubMed]
- Spoelstra, A.; de Martino Norante, L.; Terra, W.; Sciacchitano, A.; Scarano, F. On-site cycling drag analysis with the Ring of Fire. Exp. Fluids 2019, 60, 90. [Google Scholar] [CrossRef]
- Scarano, F.; Ghaemi, S.; Caridi, G.C.A.; Bosbach, J.; Dierksheide, U.; Sciacchitano, A. On the use of helium-filled soap bubbles for large-scale tomographic PIV in wind tunnel experiments. Exp. Fluids 2015, 56, 42. [Google Scholar] [CrossRef]
- Edwards, A.G.; Byrnes, W.C. Aerodynamic characteristics as determinants of the drafting effect in cycling. Med. Sci. Sports Exerc. 2007, 39, 170–176. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).