Difference of Reynolds Crisis Aspects on Soccer Balls and Their Panels †
Abstract
1. Introduction
2. Method
2.1. Fluid Force Experiment 1
2.2. Groove Shape Measurement
2.3. Oil Film Experiment/2D-PIV Measurement
3. Result and Discussion
3.1. Fluid Force Experiment
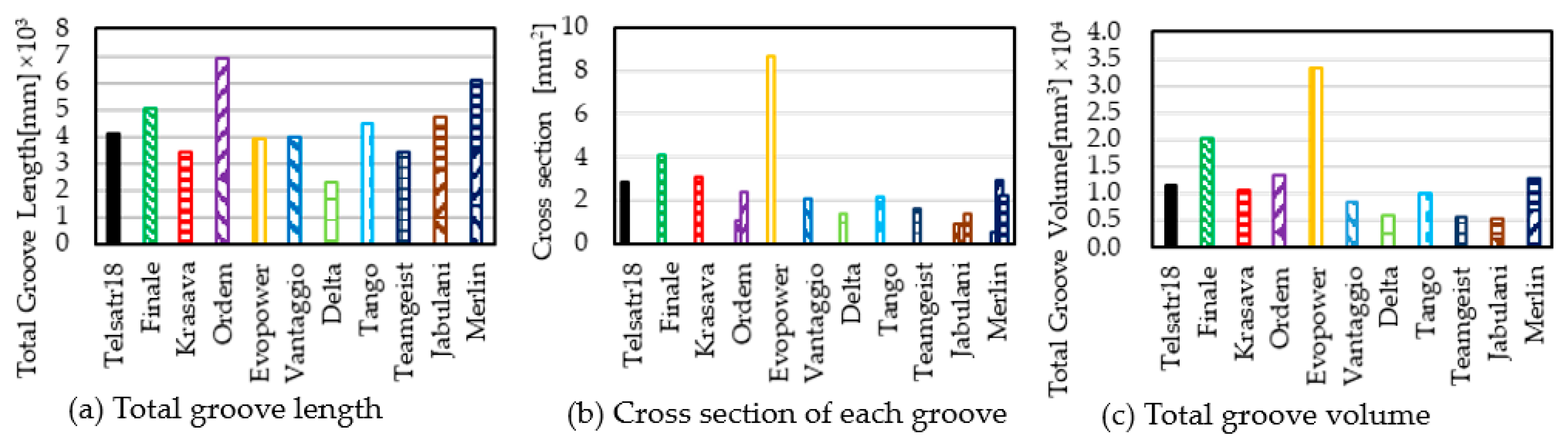
3.2. Groove Shape Measurement
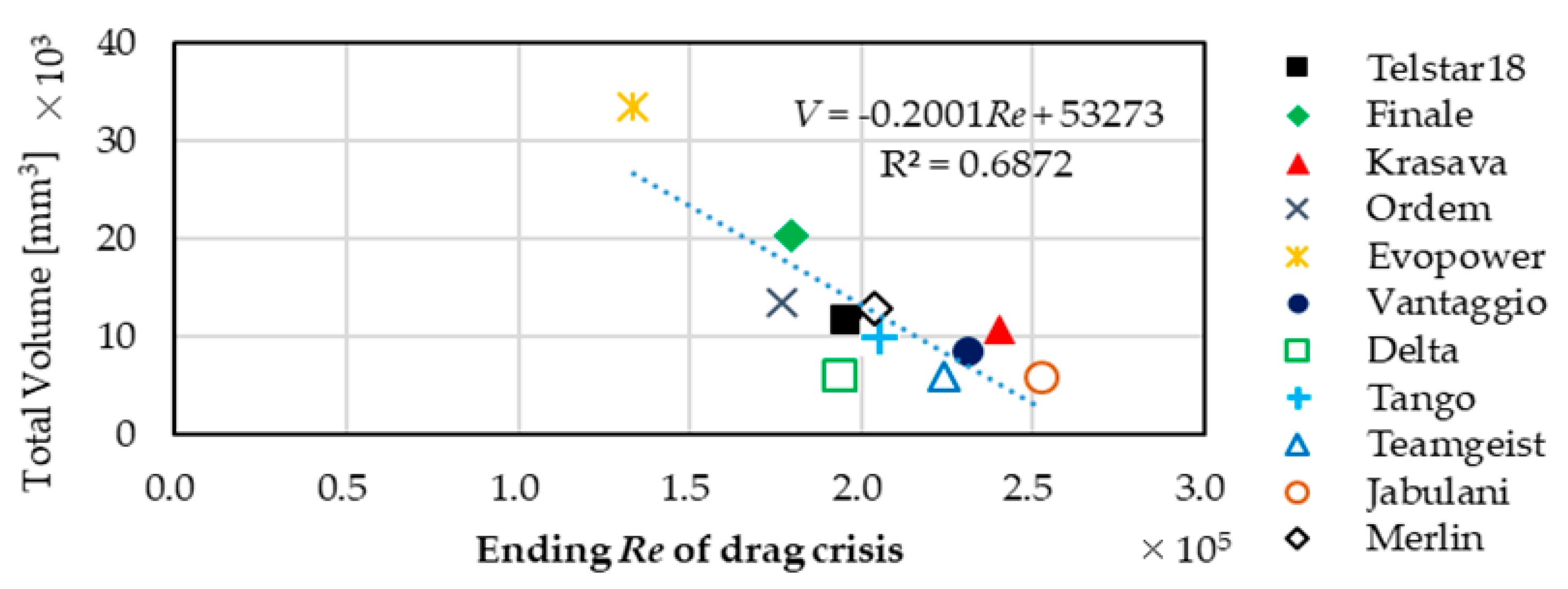
3.3. Oil Film Experiment/2D-PIV Measurement
4. Conclusions
- The CD diagrams and also the aspects of the drag crisis were different from the panel shape.
- The total volume of the groove affects the Reynolds number at which the drag crisis occurs. The panel groove affects the shape of the drag crisis.
- The position of the flow separation point did not change in the subcritical and supercritical regions by the ball orientation.
- The aspect change of the drag crisis in panel difference causes the panel groove mixed with laminar and turbulent regions.
References
- Passmore, M.; Rogers, D.; Tuplin, S.; Harland, A.; Lucas, T.; Holmes, C. The aerodynamic performance of a range of FIFA-approved footballs. J. Sports Eng. Technol. 2012, 226, 61–70. [Google Scholar] [CrossRef]
- Goff, J.E.; Asai, T.; Hong, S. A comparison of Jabulani and Brazuca non-spin aerodynamics. J. Sports Eng. Technol. 2014, 228, 188–194. [Google Scholar] [CrossRef]
- Goff, J.E.; Hong, S.; Asai, T. Aerodynamic and surface comparisons between Telstar 18 and Brazuca. J. Sports Eng. Technol. 2018, 232, 342–348. [Google Scholar] [CrossRef]
- Hong, S.; Asai, T.; Seo, K. Flow Visualization around Panel Shapes of Soccer Ball. Procedia Eng. 2015, 112, 391–394. [Google Scholar] [CrossRef][Green Version]
- Hong, S.; Asai, T.; Seo, K. Visualization of air flow around soccer ball using a particle image velocimetry. Sci. Rep. 2015, 5, 15108. [Google Scholar] [CrossRef] [PubMed]
- Murakami, M.; Kondoh, M.; Iwai, Y.; Seo, K. Measurement of aerodynamic forces and flow field of a soccer ball in a wind tunnel for knuckle effect. Procedia Eng. 2010, 2, 2467–2472. [Google Scholar] [CrossRef][Green Version]


| Name | Merlin | Telstar18 | Krasava | Ordem | Finale | Vantaggio | |
| Design |  |  |  |  |  |  | |
| Exp. | Fluid force | done | done | done | done | done | done |
| Oil film | done | done | done | done | |||
| PIV | done | done | |||||
| Name | Evopower | Delta | Tang12 | Jabulani | TeamGeist | ||
| Design |  |  |  |  |  | ||
| Exp. | Fluid force | done | done | done | done | done | |
| Oil film | |||||||
| PIV | done | done | done | ||||
| No. | Panel Orientation and Laser Position | Subcritical (5 m/s) Re = 7.3 × 104 | Critical (8 m/s) Re = 1.2 × 105 | Supercritical (15 m/s) Re = 2.2 × 105 |
|---|---|---|---|---|
| a |  | |||
| b | ||||
| c | ||||
| No. | Panel Orientation and Laser Position | Subcritical (9 m/s) Re = 1.3 × 105 | Critical (12.5 m/s) Re = 1.8 × 105 | Supercritical (20 m/s) Re = 2.9 × 105 |
|---|---|---|---|---|
| a | 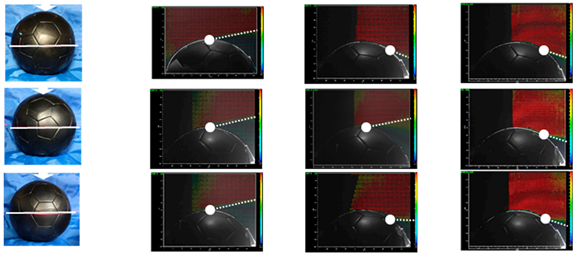 | |||
| b | ||||
| c | ||||
| No. | Panel Orientation and Laser Position | Subcritical (5 m/s) Re = 7.3 × 104 | Critical (14 m/s) Re = 2.1 × 105 | Supercritical (20 m/s) Re = 2.9 × 105 |
|---|---|---|---|---|
| a | 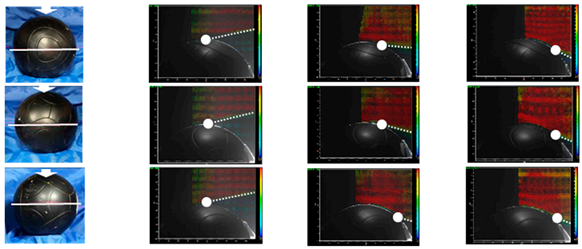 | |||
| b | ||||
| c | ||||
| No. | Panel Orientation and Laser Position | Subcritical (5 m/s) Re = 7.3 × 104 | Critical (12.5 m/s) Re = 1.8 × 105 | Supercritical (20 m/s) Re = 2.1 × 105 |
|---|---|---|---|---|
| a | 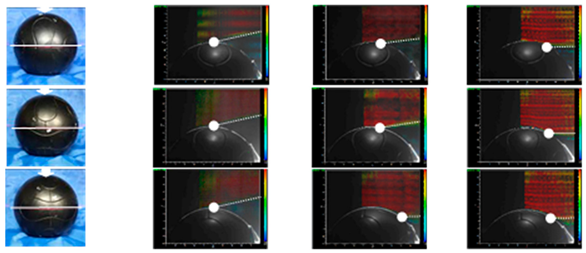 | |||
| b | ||||
| c | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakamoto, Y.; Ito, S.; Hiratsuka, M. Difference of Reynolds Crisis Aspects on Soccer Balls and Their Panels. Proceedings 2020, 49, 117. https://doi.org/10.3390/proceedings2020049117
Sakamoto Y, Ito S, Hiratsuka M. Difference of Reynolds Crisis Aspects on Soccer Balls and Their Panels. Proceedings. 2020; 49(1):117. https://doi.org/10.3390/proceedings2020049117
Chicago/Turabian StyleSakamoto, Yuki, Shinichiro Ito, and Masaki Hiratsuka. 2020. "Difference of Reynolds Crisis Aspects on Soccer Balls and Their Panels" Proceedings 49, no. 1: 117. https://doi.org/10.3390/proceedings2020049117
APA StyleSakamoto, Y., Ito, S., & Hiratsuka, M. (2020). Difference of Reynolds Crisis Aspects on Soccer Balls and Their Panels. Proceedings, 49(1), 117. https://doi.org/10.3390/proceedings2020049117




