Earthquake Magnitude Prediction Using Recurrent Neural Networks ^†

Abstract

The importance of seismological research around the globe is very clear. Therefore, new tools and algorithms are needed in order to predict magnitude, time, and geographic location, as well as to discover relationships that allow us to better understand this phenomenon and thus be able to save countless human lives. However, given the highly random nature of earthquakes and the complexity in obtaining an efficient mathematical model, efforts until now have been insufficient and new methods that can contribute to solving this challenge are needed. In this work, a novel earthquake magnitude prediction method is proposed, which is based on the composition of a known system whose behavior is governed according to the measurements of more than two decades of seismic events and is modeled as a time series using machine learning, specifically a network architecture based on LSTM (long short-term memory) cells.

1. Introduction

Natural disasters are without any doubt a latent danger and become very devastating and threaten the entire ecosystem of one region. That is why the prediction of earthquakes plays such an important role since its goal is to specify the magnitude and geographical and temporary location of future earthquakes with enough precision and anticipation to issue a warning. Despite the efforts made to produce mechanical or computational models of the earthquake process, these still do not achieve real predictive power. Given the highly random nature of earthquakes with relatively high magnitude, their occurrence can only be analyzed using a statistical approach, but any synthetic model must show the same characteristics with respect to its distribution in size, time, and space, which is very hard to achieve [1].

Earthquake prediction can be separated into three main categories, namely, short-term, intermediate-term, and long-term prediction, whose difference is in the type of analysis and the time considered to make the prediction. When we talk about the short-term category, the so-called precursors, which are phenomena or anomalies that precede the earthquake, are the main parameters used for making predictions. Rikitake [2] compiled almost 400 precursors that could give clues of a possible large magnitude earthquake.

The intermediate-term and long-term prediction categories look for trends or patterns in the seismic-related signals recorded during periods that go from 1 to 10 years and from 10 years and above, respectively. There are different techniques for intermediate-term prediction, such as the CN algorithm (earthquakes with M > 6.5 in California and Nevada), MSc (Mendocino Scenario) algorithm and M8 algorithm, whereas for long-term predictions, despite the serious efforts and the several developed models, no efficient technique has yet been established [3].

Currently, with increasing computational power and existing data processing tools, several techniques have been proposed such as the one developed by Wang et al. [4], who used long short-term memory (LSTM) networks to learn the spatio-temporal relationship between earthquakes in different locations and make predictions on the basis of such a relationship. For the prediction of the magnitude of an earthquake in the region of Hindukush, Asim et al. [5] used machine learning techniques, including pattern recognition neural network, RNN (recurrent neural network), random forest, and linear programming boost classifier, formulating the problem as a binary classification task, and making a prediction of earthquakes with magnitudes greater than or equal to 5.5 in a time interval of 1 month. Narayanakumar and Raja [6] evaluated the performance of BP (backpropogation) neural network techniques in predicting earthquakes occurring in the region of the Himalayan belt using different types of input data.

In the present work, we propose a short-term prediction of earthquake magnitude in Italy using a database of seismic events spanning over more than 20 years, by using a recurrent neural network model. The short-term earthquake prediction is very challenging, because large earthquakes cannot be reliably predicted for specific regions over time scales less than decades [7].

2. Methods

2.1. Time Series Modeling with the LSTM Recurrent Neural Networks

Unlike traditional neural networks, the LSTM recurrent neural network is an extremely efficient tool when the information is sequential. The basic condition of LSTM modeling is that all inputs and outputs are independent of each other. However, the dynamic nonlinear system has the following form:

$$y\left(k\right)=\Phi \left[y\right(k-1),\cdots ,y(k-n_y),u(k),\cdots ,u(k-n_u\left)\right]$$

(1)

where $\Phi (\cdot )$ is an unknown nonlinear difference equation representing the plant dynamics, $u\left(k\right)$ and $y\left(k\right)$ are measurable scalar input and output, and $n_y$ and $n_u$ are the last values of the output and input, respectively, to be considered for the system dynamics. Then, the time series can be identified by the following prediction model:

$$y\left(k\right)=N\left[y\right(k-1),\cdots ,y(k-m\left)\right]$$

(2)

where m is the regression order for the output $y\left(k\right)$.

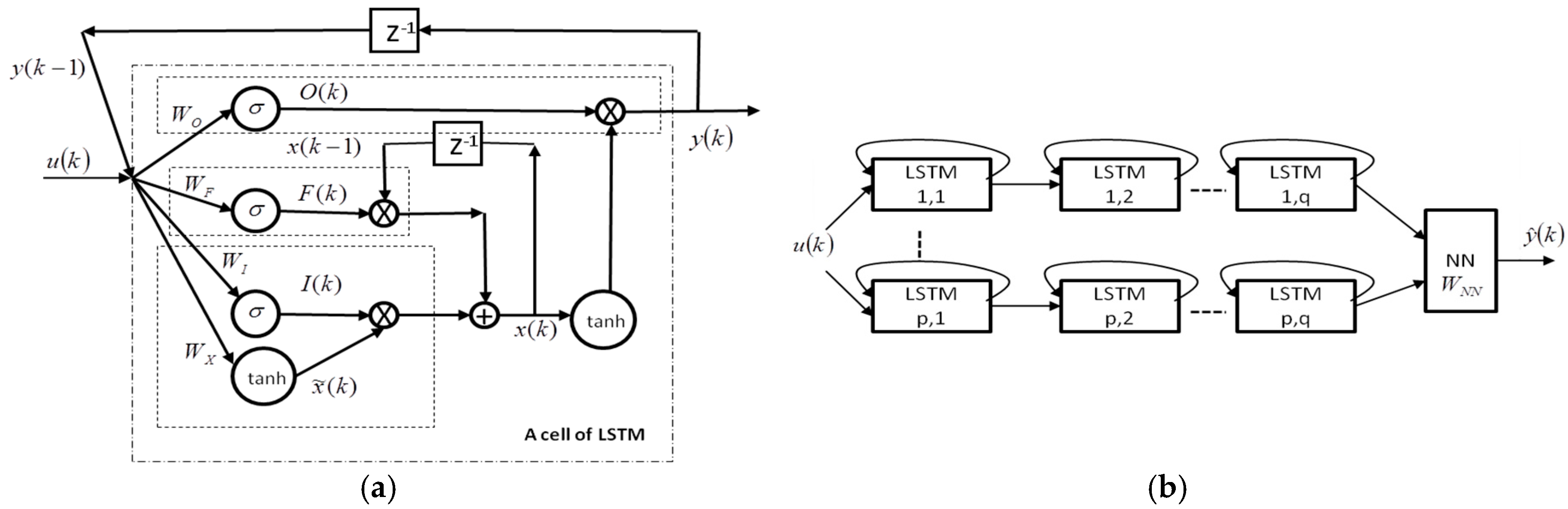
Connecting previous information to the present task depends on many factors, but LSTM recurrent neural networks can learn to use the past information. In theory, any recurrent neural network (RNN) can handle such long-term dependencies by picking certain parameters, but in practice it does not seem to be able to learn them; however, LSTM networks use gate cells to remember them. The key gate to LSTMs is the cell state. An LSTM cell has three gates to protect and control the cell state, namely, forget gate, input gate, and output gate, as shown in Figure 1a.

The object of time series modeling using LSTM is to update the weights $W_F$, $W_I$, $W_X$, and $W_O$, such that the output of the LSTM neural network converges to the system output $y\left(k\right)$ in Equation (1):

$${argmin}_{W_F,W_I,W_X,W_O}\left[y\right(k)-y(k\left)\right]²$$

(3)

$$.$$

(3)

In this paper, we combine classical neural networks with LSTM. This neural model [8] is shown in Figure 1b. Here, we use $p\times q$ LSTMs, which are connected in simple feedforward form. The final $p$ LSTMs are fully connected to a multilayer perceptron.

2.2. Earthquake Magnitude Prediction as a Time Series Modeling Problem

In the present work, we analyzed the Italian seismic catalog of earthquakes with magnitude equal to or larger than 1.5 from 1995 to 2018.

For each seismic event, variables such as latitude, longitude, and depth of the hypocenter, time of occurrence, and magnitude are treated as a function $E\left(P\right(k\left)\right)$ that represents a set of samples over time, where $k=1,...,N$ with $N$ is the total number of samples taken in that period of time, and $P\left(k\right)$ is a vector of parameters derived from those variables.

The goal is to find a relationship between past and future events in order to predict the magnitude of upcoming events, with an acceptable error using the actual information. Given the seemingly random nature of the problem, it is difficult to find such a relationship between the different variables and their derivatives; moreover, it is also difficult to know to what extent they influence the magnitude of a future event.

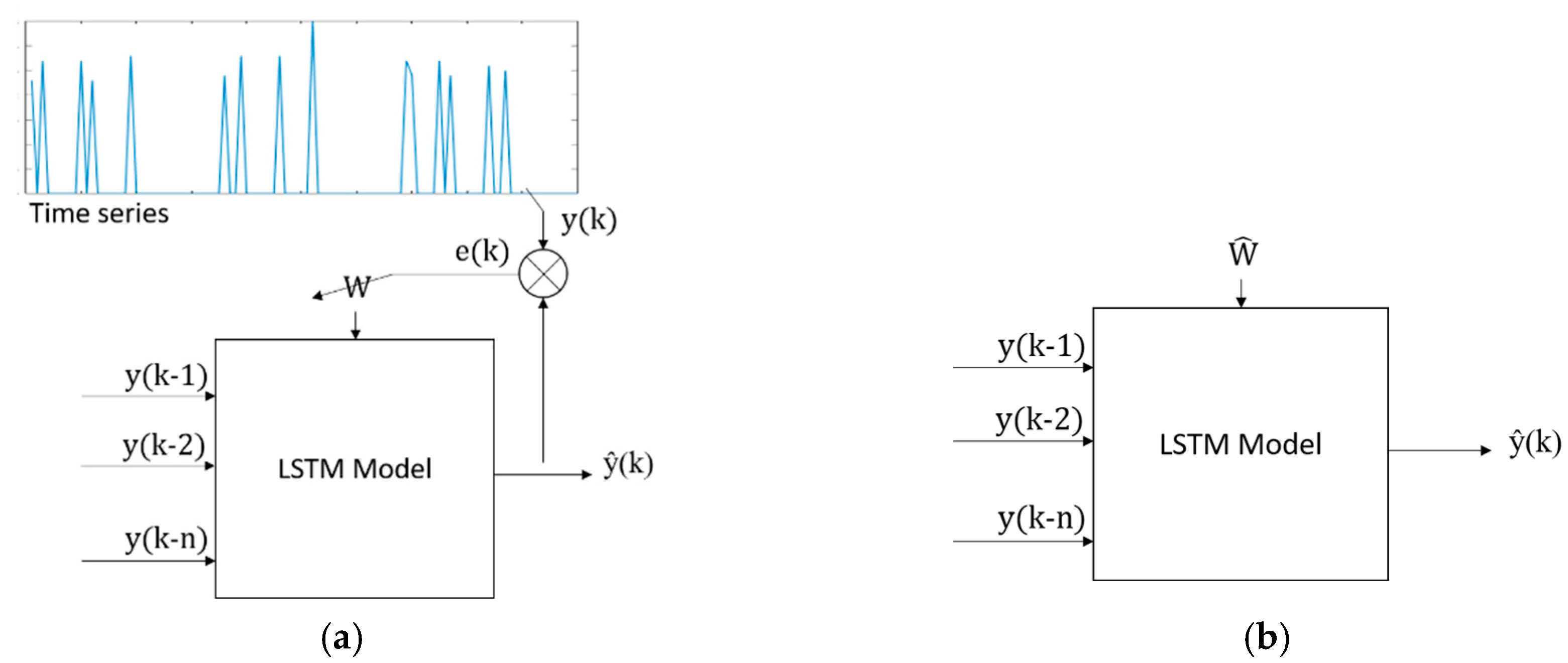
Therefore, the following basic model to be learned is proposed:

$$y\left(k\right)=N\left[y\right(k-1),\cdots ,y(k-n\left)\right]$$

(4)

where $y\left(k\right)$ represents the magnitude of an event at time $k$. Figure 2 represents the model shown in Equation (4) for training (Figure 2a) and prediction (Figure 2b). Such a model will be used throughout the present work.

3. Results and Discussion

In this work, we divided the whole observation period in non-overlapping windows of 1 h duration and considered only the event with the largest magnitude which occurred in each hourly window.

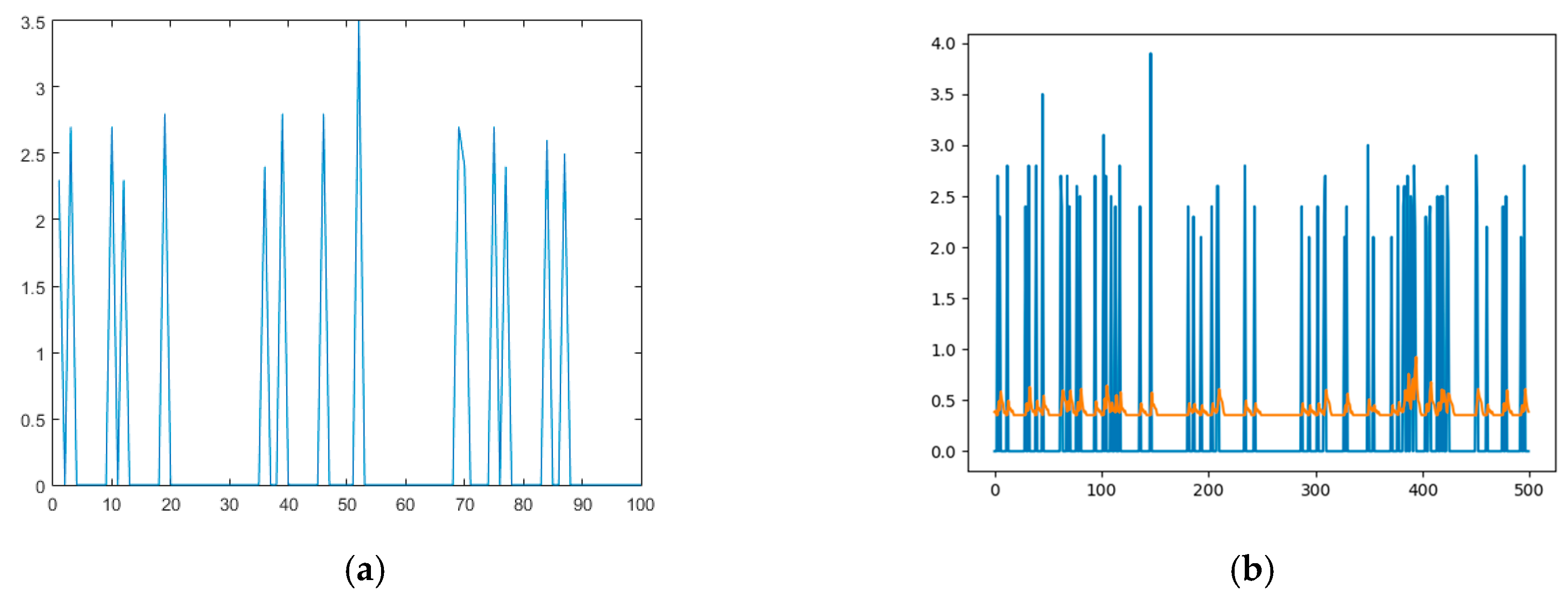
Figure 3a shows, an as example, the first 100 h of our magnitude time series. Some windows have magnitude 0, which means that no earthquakes occurred. Actually, these values are not part of the behavior of the system and they make the training of the network very difficult, as shown in Figure 3b.

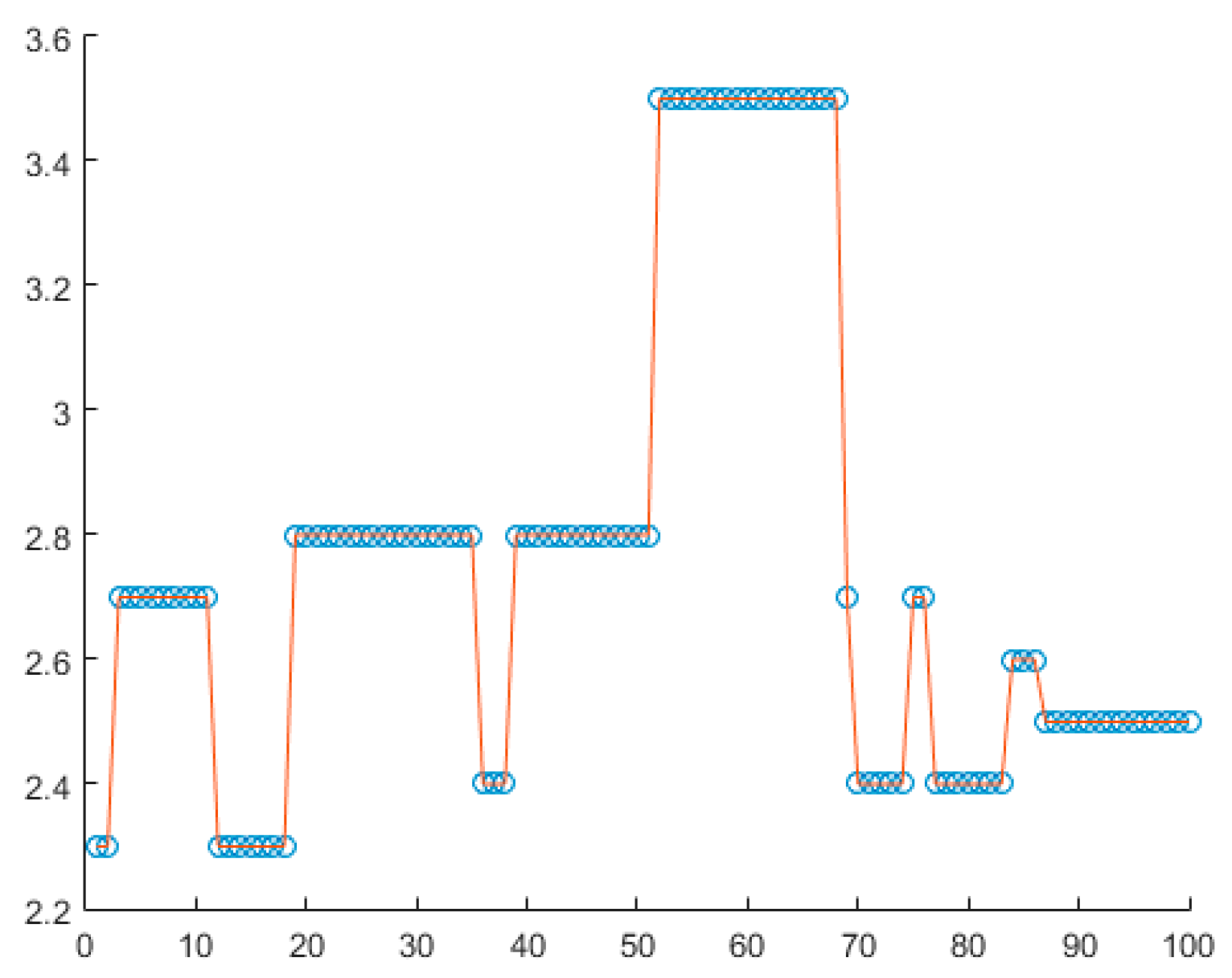
Therefore, it is then possible to take the zero-order hold model of the time series generating a new function that nevertheless reproduces the original behavior, keeping all the peaks that correspond to the magnitudes of the events, see Figure 4.

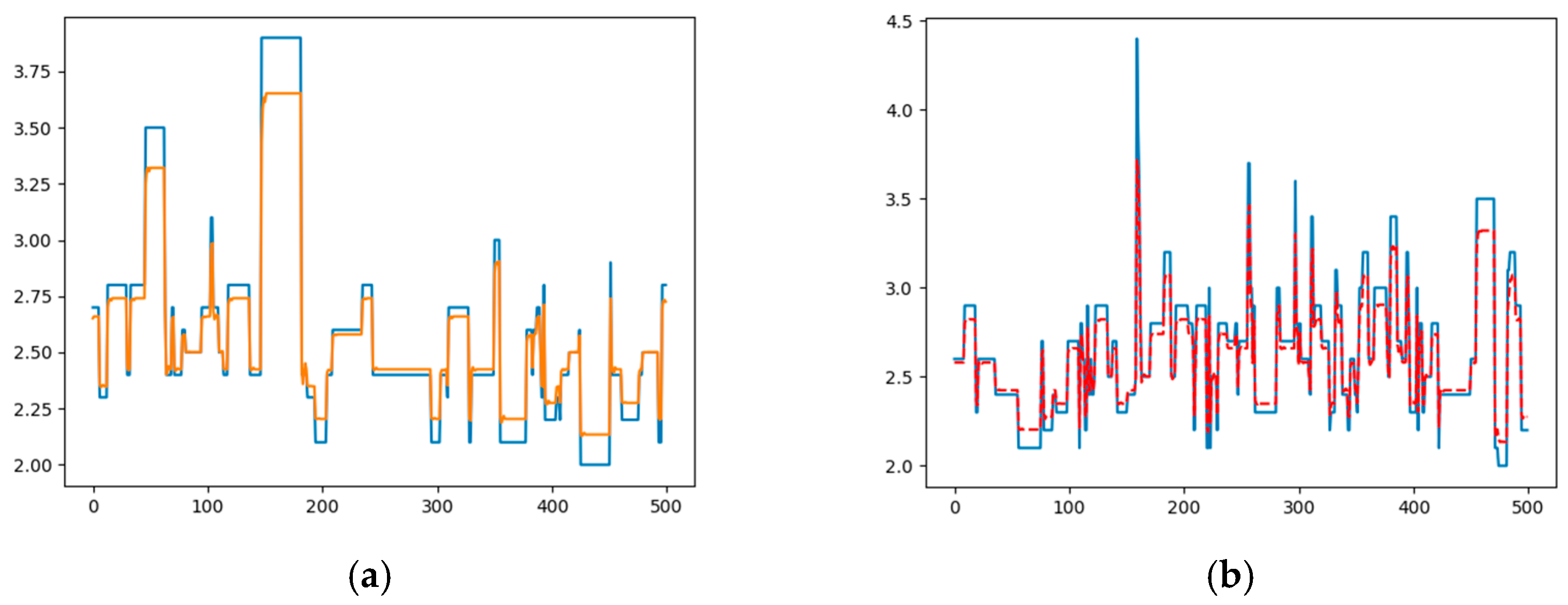
Using the architecture proposed above with $n=5$, which was the minimum delay to get a good result, and with 10% of the data used for training and 2 epochs, we get a training error of 0.002 and a prediction error of 0.003 (Figure 5).

The accuracy of this prediction depends on the absence of contiguous events in the original time series with the same magnitude. However, in our seismic dataset, no contiguous hourly windows were found with the same maximum magnitude.

Then, after training the model, in the prediction we returned to zero all those values that were used to fill the zeros in the original series, obtaining the original model as shown in Figure 6.

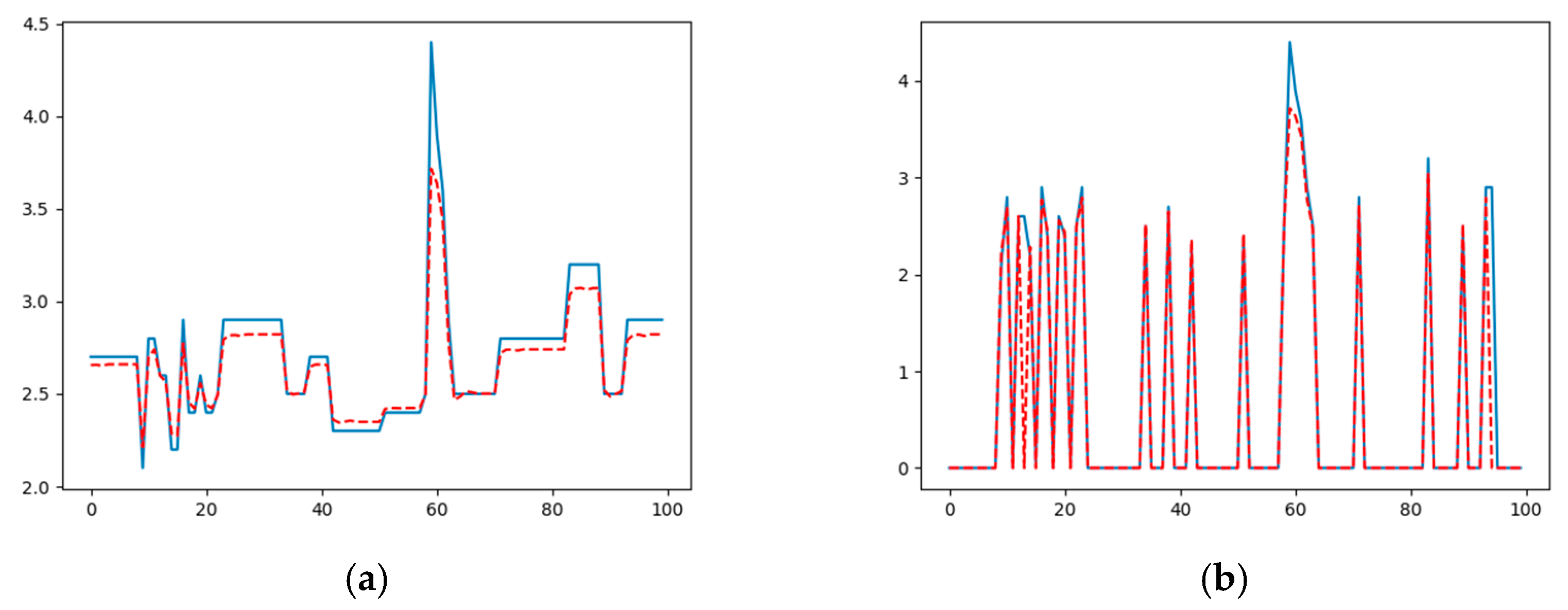
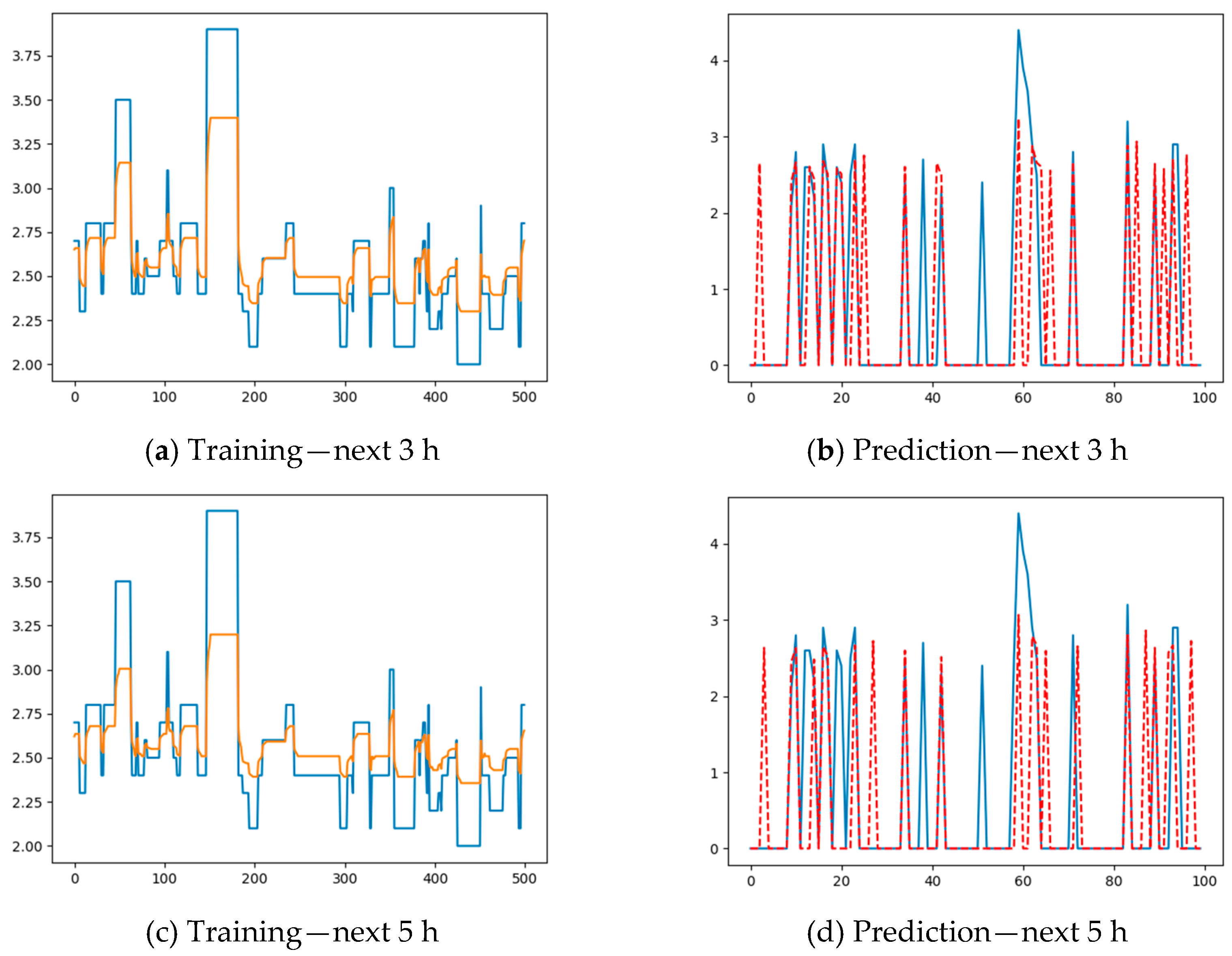
Using this procedure, the prediction of the maximum magnitude in the next hour can be performed with a minimum error. However, the prediction of the maximum magnitude in the next 3 h, using as an input $y(k-3),\cdots ,y(k-8)$, or in the next 5 h, using as input $y(k-5),\cdots ,y(k-10)$, does not furnish good results, since the prediction error grows quite rapidly, as shown in Figure 7b,d.

In the present work, we considered the maximum magnitude of events occurring in 1 h. If the size of the window becomes 1 day, the pattern of the zeros, as shown in Figure 3a, changes, because the zero values become less numerous, and the prediction becomes more complex.

If we raise the magnitude threshold of the catalog from 1.5 to 2, the pattern becomes similar and the same model previously analyzed can be applied. If we need to predict the maximum magnitude of the events on a monthly basis, then the threshold magnitude should be even higher to obtain a similar pattern, but the number of monthly windows would be lower than that of the daily or hourly windows, which is not enough to obtain reliable predictions.

4. Conclusions

In this work, the prediction of the largest magnitude of the events occurring in the next hour was performed by using a recurrent neural network model and applying it to the seismic catalogue of Italy spanning from 1995 to 2018. Our recurrent neural network model was found to be good enough to make a prediction of the magnitude of earthquakes, taking as the only available information the series of magnitudes. However, since earthquakes are characterized by several variables, these could be added to the network and possibly find more robust patterns that could further minimize the prediction error.