Dynamic Fracture Process and Strain Rate Effect of a Porous SiC Ceramic †
Abstract
:1. Introduction
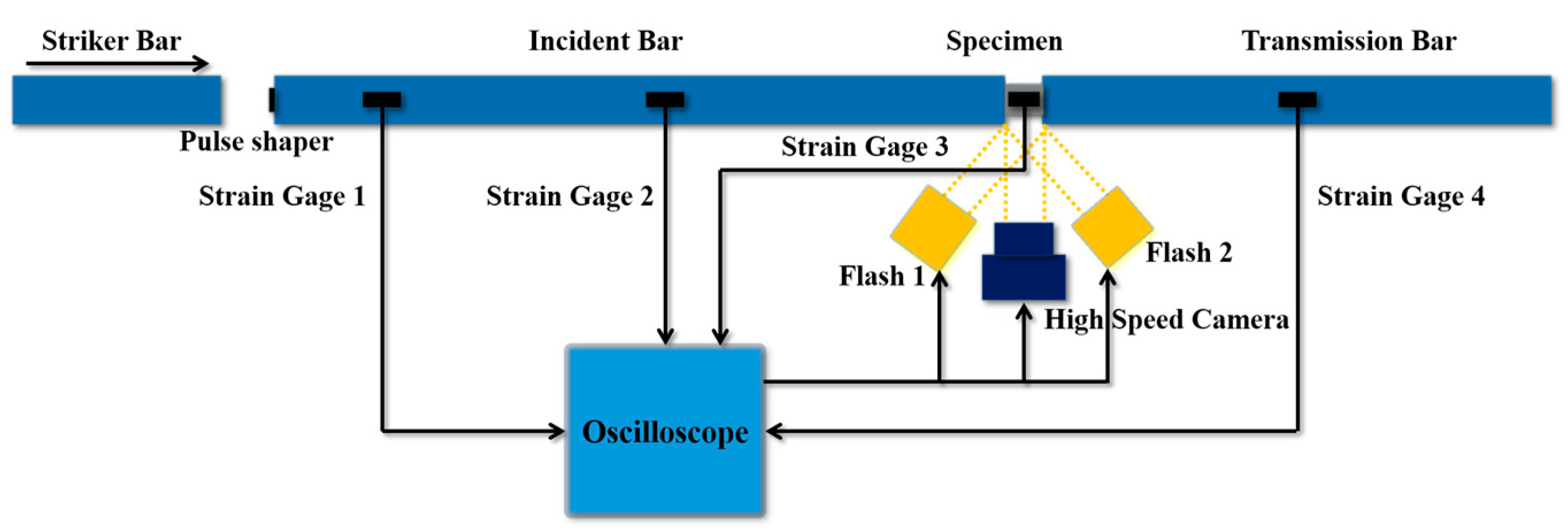
2. Material and Experiment
3. Results and Discussion
3.1. Experimental Data
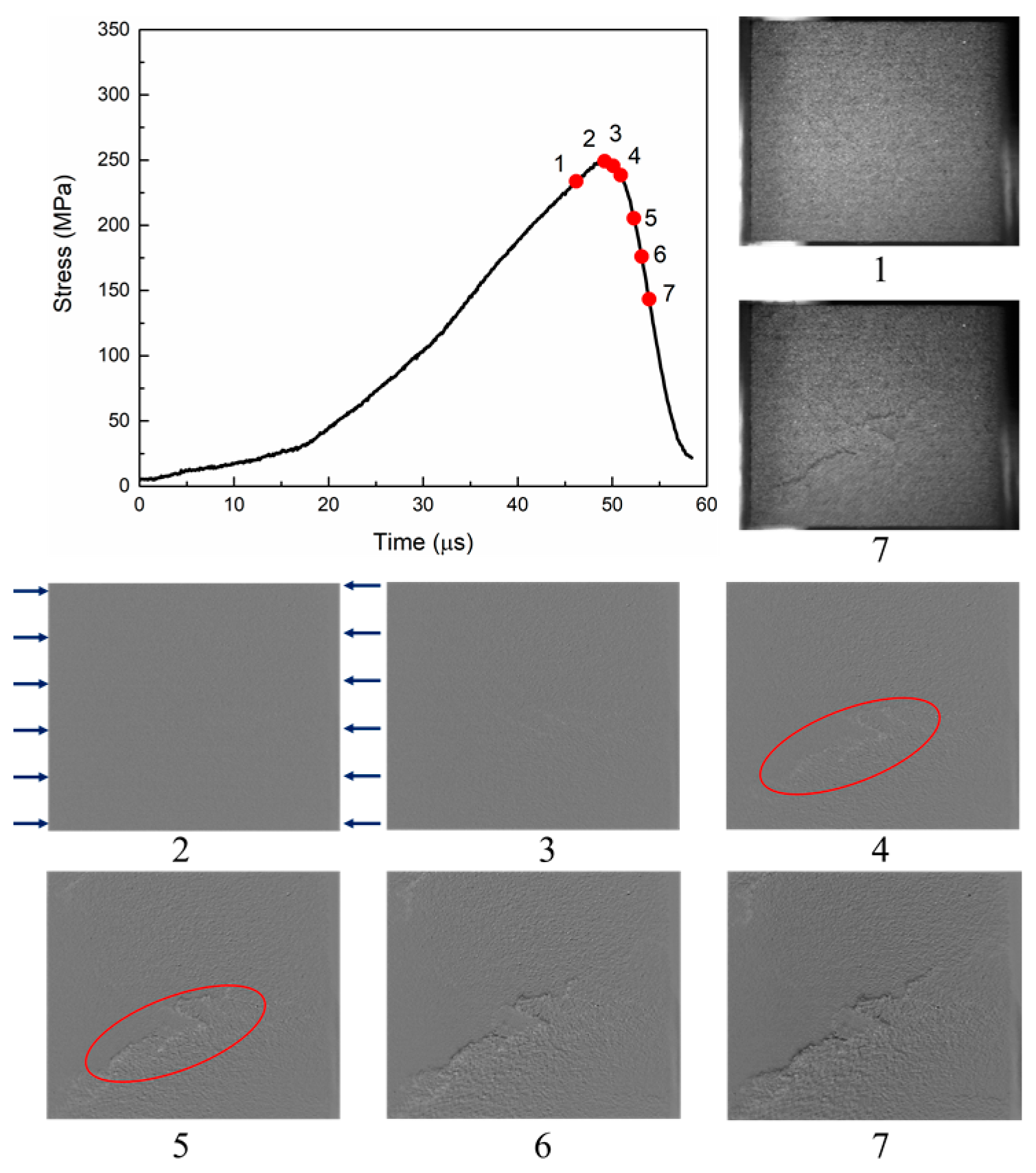
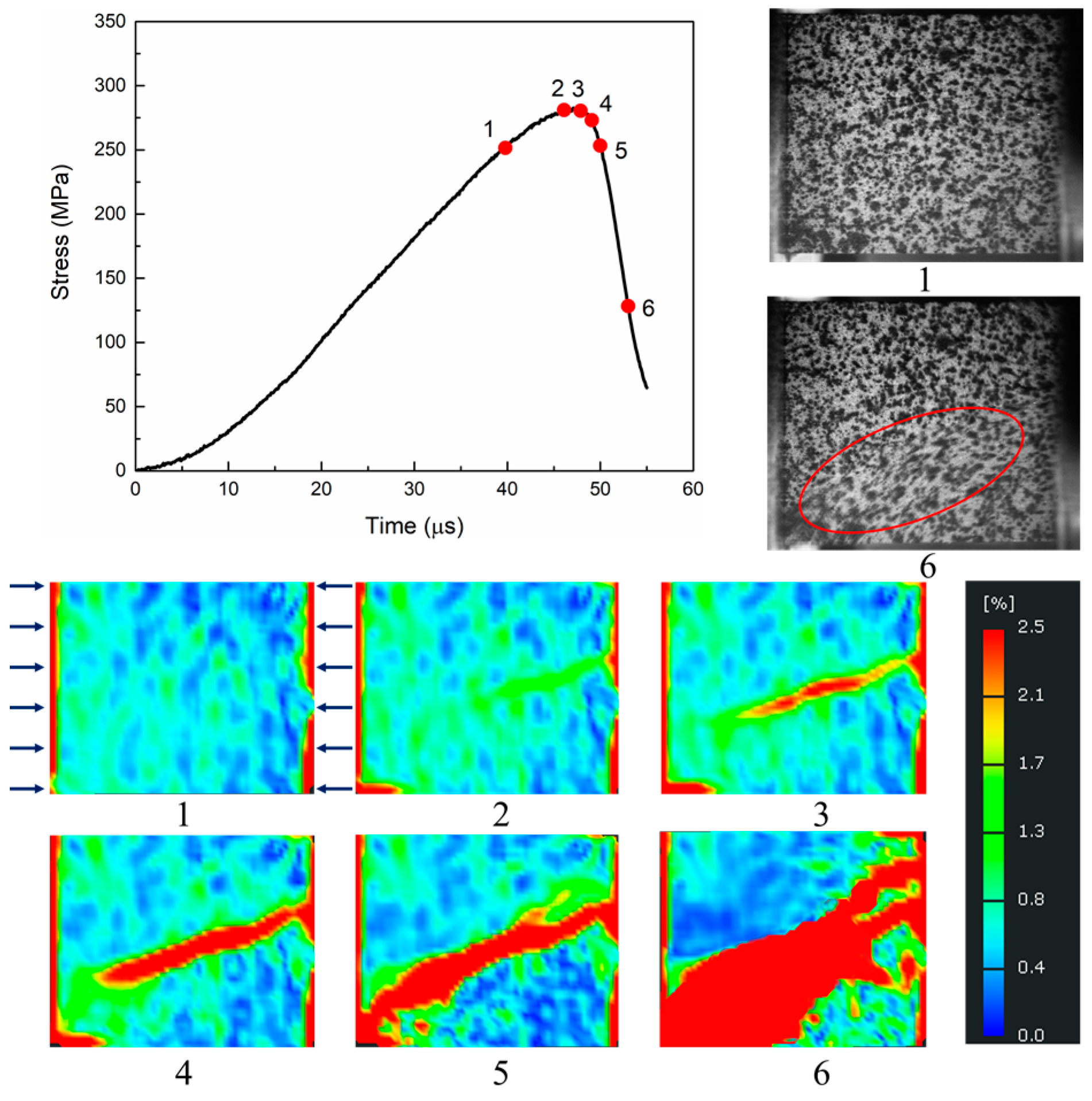
3.2. Fracture Process
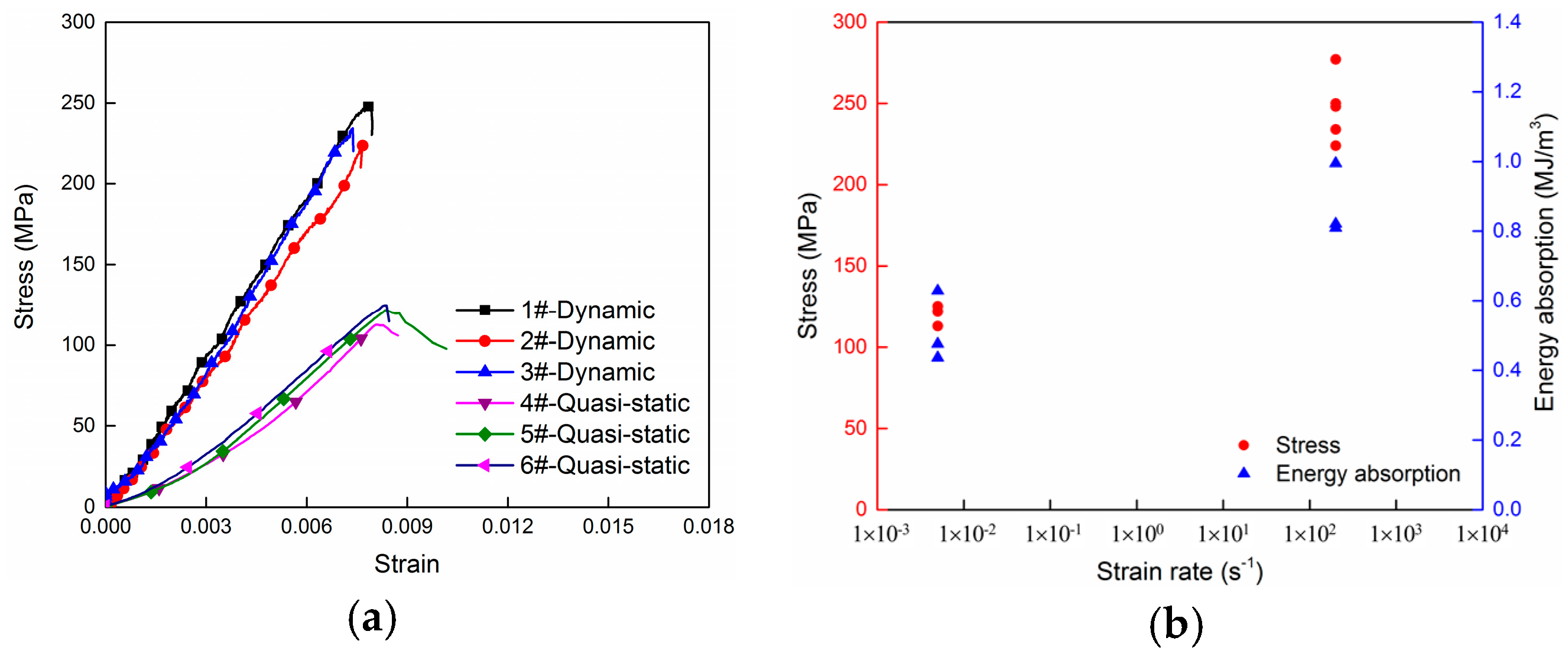
3.3. Strain Rate Effect
4. Conclusions
- Three methods were used to measure the strain of the specimen during deformation and the results show that DIC method is the best while strain gage mounted on the specimen is also reliable. However, strain calculated by SHPB method is not suitable for brittle materials like porous SiC ceramic.
- The high-speed images showed that crack initiates in the center of the specimen and then propagates to the entire specimen under dynamic loading. The velocity of the crack propagation is about 1000 m/s. The zig-zag crack was found on the surface of the specimen. Main cracks occurred after the peak stress was achieved. DIC results verified the failure process.
- Dynamic strength of the material is much higher than the quasi-static strength which shows obviously positive strain rate effect of the porous SiC ceramic. Energy absorption during the deformation process is much larger under dynamic loading.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Wang, F.; Yin, J.; Yao, D.; Xia, Y.; Zuo, K.; Xu, J.; Zeng, Y. Fabrication of porous SiC ceramics through a modified gelcasting and solid state sintering. Mater. Sci. Eng. A 2016, 654, 292–297. [Google Scholar] [CrossRef]
- Wang, F.; Yao, D.; Xia, Y.; Zuo, K.; Xu, J.; Zeng, Y. Porous SiC ceramics prepared via freeze-casting and solid state sintering. Ceram. Int. 2016, 42, 4526–4531. [Google Scholar] [CrossRef]
- Wu, H.; Li, Y.; Yan, Y.; Yin, J.; Liu, X.; Huang, Z.; Lee, S.-H.; Jiang, D. Processing, microstructures and mechanical properties of aqueous gelcasted and solid-state-sintered porous SiC ceramics. J. Eur. Ceram. Soc. 2014, 34, 3469–3478. [Google Scholar] [CrossRef]
- Chi, W.; Jiang, D.; Huang, Z.; Tan, S. Sintering behavior of porous SiC ceramics. Ceram. Int. 2004, 30, 869–874. [Google Scholar] [CrossRef]
- Alvin, M.A. Impact of char and ash fines on porous ceramic filter life. Fuel Process. Technol. 1998, 56, 143–168. [Google Scholar] [CrossRef]
- Li, J.; Lin, H.; Li, J. Factors that influence the flexural strength of SiC-based porous ceramics used for hot gas filter support. J. Eur. Ceram. Soc. 2011, 31, 825–831. [Google Scholar] [CrossRef]
- Deng, Z.-Y.; She, J.; Inagaki, Y.; Yang, J.-F.; Ohji, T.; Tanaka, Y. Reinforcement by crack-tip blunting in porous ceramics. J. Eur. Ceram. Soc. 2004, 24, 2055–2059. [Google Scholar] [CrossRef]
- Martin, S.R. Effects of Porosity Distribution on the Dynamic Behavior of Two Varieties of SiC; Defense Technical Information Center: Fort Belvoir, VA, USA, 2004. [Google Scholar]
- Hu, G.; Ramesh, K.T.; Cao, B.; McCauley, J.W. The compressive failure of aluminum nitride considered as a model advanced ceramic. J. Mech. Phys. Solids 2011, 59, 1076–1093. [Google Scholar] [CrossRef]



| Loading Conditions | σ (MPa) | ε (%) |
|---|---|---|
| Quasi-static | 113 | 0.81 |
| 122 | 0.84 | |
| 125 | 0.84 | |
| Average | 120 | 0.83 |
| Dynamic | 248 | 0.79 |
| 224 | 0.77 | |
| 234 | 0.74 | |
| 250 | 0.81 | |
| 277 | 0.84 | |
| Average | 247 | 0.79 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhou, D.; Liu, H.; Zakir, S.M.; Li, Y. Dynamic Fracture Process and Strain Rate Effect of a Porous SiC Ceramic. Proceedings 2018, 2, 509. https://doi.org/10.3390/ICEM18-05409
Wang Y, Zhou D, Liu H, Zakir SM, Li Y. Dynamic Fracture Process and Strain Rate Effect of a Porous SiC Ceramic. Proceedings. 2018; 2(8):509. https://doi.org/10.3390/ICEM18-05409
Chicago/Turabian StyleWang, Yanpei, Ding Zhou, Huifang Liu, Sheikh Muhamamd Zakir, and Yulong Li. 2018. "Dynamic Fracture Process and Strain Rate Effect of a Porous SiC Ceramic" Proceedings 2, no. 8: 509. https://doi.org/10.3390/ICEM18-05409
APA StyleWang, Y., Zhou, D., Liu, H., Zakir, S. M., & Li, Y. (2018). Dynamic Fracture Process and Strain Rate Effect of a Porous SiC Ceramic. Proceedings, 2(8), 509. https://doi.org/10.3390/ICEM18-05409





