Modelling Local Bending Stiffness of Norway Spruce Sawn Timber Using Scanned Fibre Orientation †
Abstract
:1. Introduction
2. Material and Methods
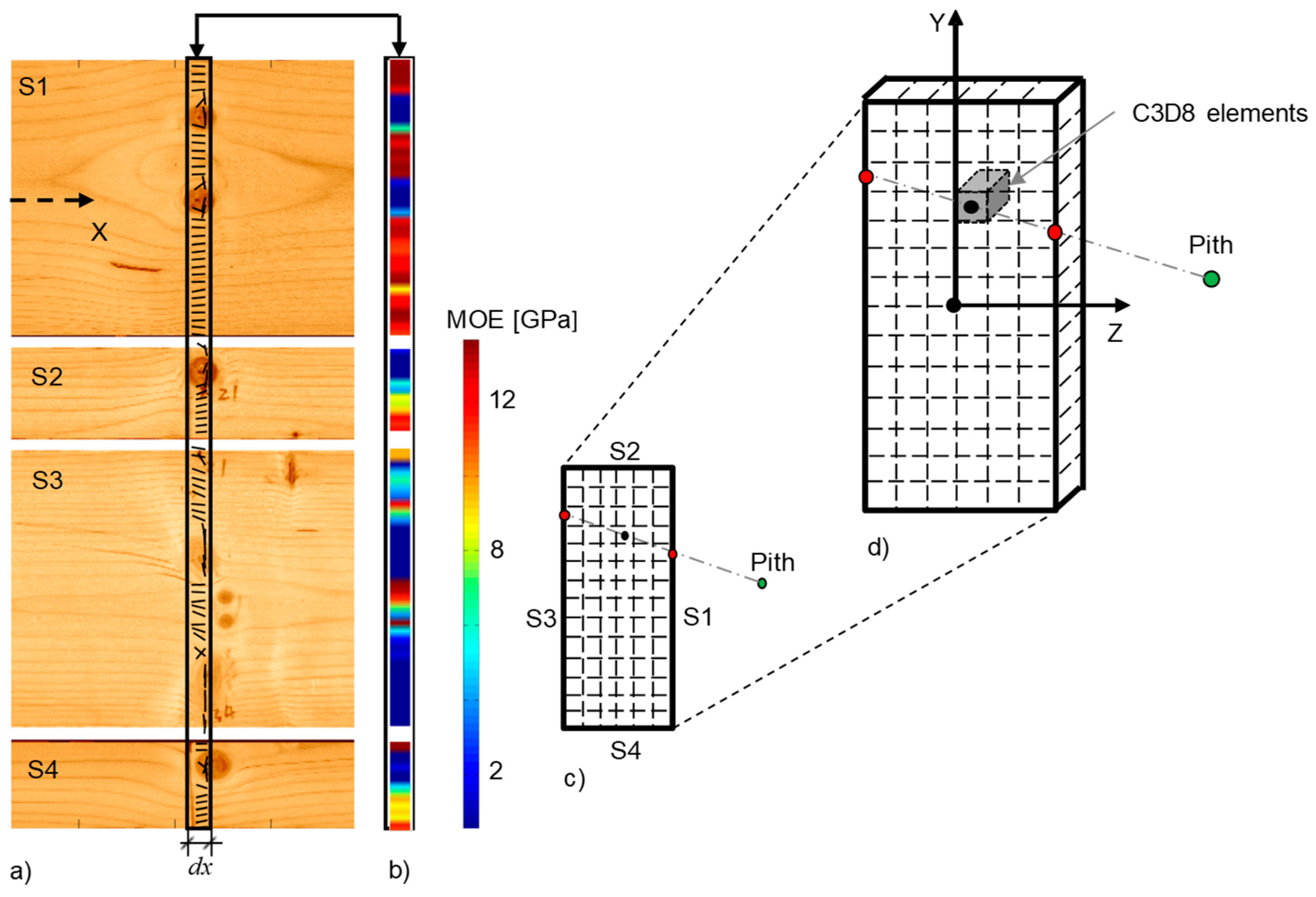
2.1. Material and Introductory Investigation
2.2. Modelling of Interior Fibre Orientation and Material Properties
2.3. FE Modelling
2.4. Laboratory Measurements by DIC
2.5. Calculation of Bending MOE
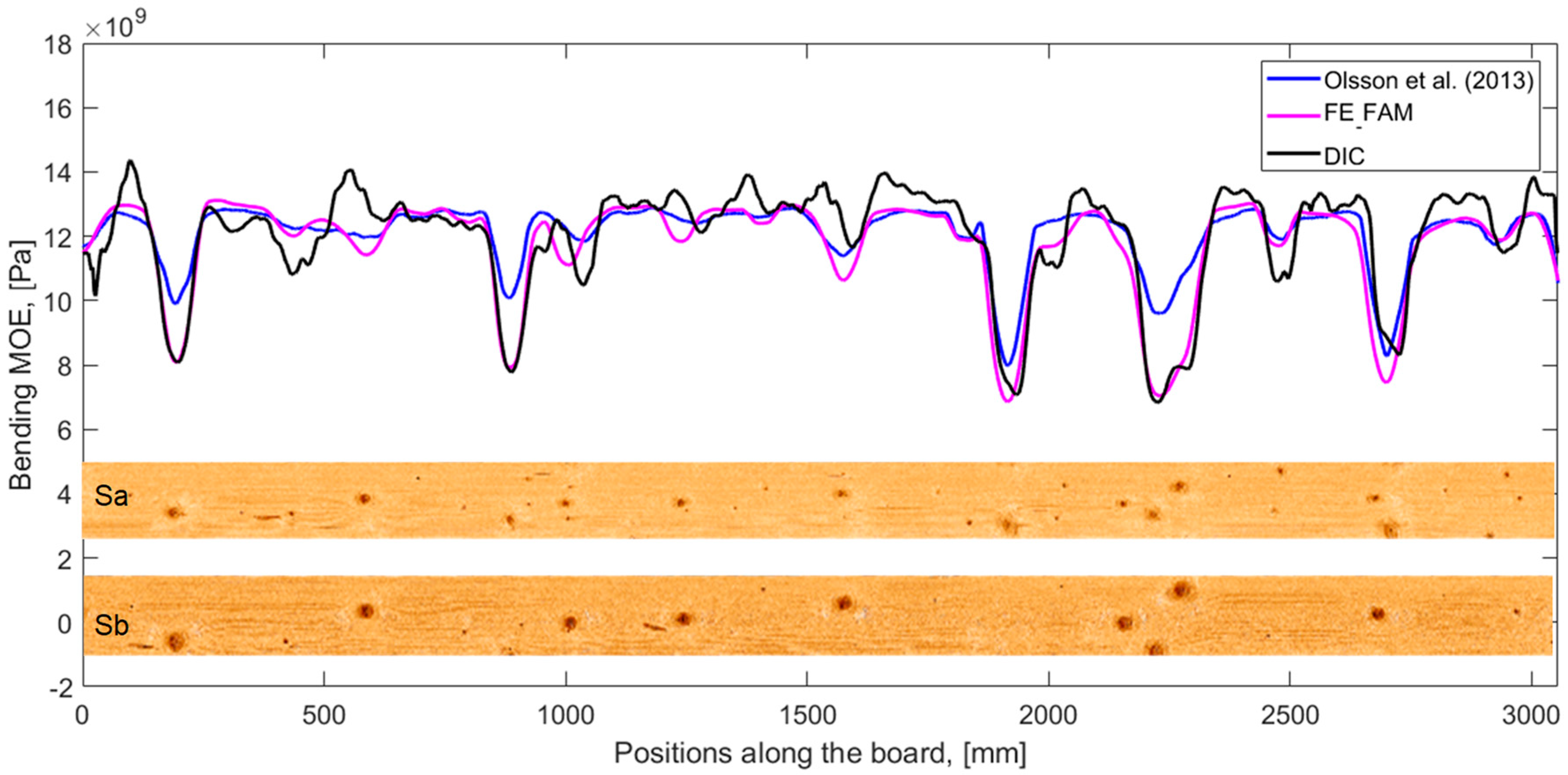
3. Results and Discussion
3.1. Strain Distribution
3.2. Bending Stiffness Variation along Boards
4. Conclusions
References
- Hankinson, R. L. Investigation of crushing strength of spruce at varying angles of grain. In Air Service Information Circular; No. 259; U. S. Air Service: Washington, DC, USA, 1921. [Google Scholar]
- Johansson, C.-J.; Boström, L.; Bräuner, L.; Hoffmeyer, P.; Holmquvist, C.; Solli, K.H. Laminations for Glued Laminated Timber—Establishment of Strength Classes and for Visual Strength Grade and Machine Settings for Glulam Laminations of Nordic Origin; SP Report 1998:38; SP Swedish National Testing and Research Institute: Borås, Sweden, 1998. [Google Scholar]
- Matthews, P.C.; Beech, B.H. Method and Apparatus for Detecting Timber Defects. U.S. Patent No. 3976384, 24 August 1976. [Google Scholar]
- Soest, J.; Matthews, P.C.; Wilson, B. A simple optical scanner for grain defects. In Proceedings of the 5th International Conference on Scanning Technology and Process Control for the Wood Products Industry, Atlanta, GA, USA, 25−27 October 1993. [Google Scholar]
- Olsson, A.; Oscarsson, J.; Serrano, E.; Källsner, B.; Johansson, M.; Enquist, B. Prediction of timber bending strength and in-member cross-sectional stiffness variation on the basis of local wood fibre orientation. Eur. J. Wood Prod. 2013, 71, 319–333. [Google Scholar] [CrossRef]
- Olsson, A.; Oscarsson, J. Strength grading on the basis of high resolution laser scanning and dynamic excitation: A full scale investigation of performance. Eur. J. Wood Prod. 2017, 75, 17–31. [Google Scholar] [CrossRef]
- WoodEye, AB. Available online: http://woodeye.se/en/ (accessed on 4 October 2017).
- Dinwoodie, J.M. Timber: Its Nature and Behaviour; E & FN Spon, New Fetter Lane: London, UK, 2000; p. 109. [Google Scholar]
- Ormarsson, S. Numerical Analysis of Moisture-Related Distortions in Sawn Timber; Publication 99:7; Chalmers University of Technology: Gothenburg, Sweden, 1999. [Google Scholar]


| Board Properties | Value | |
|---|---|---|
| B1 | B2 | |
| Dimension, [mm] | 45 × 145 ×4550 | 45 × 145 ×4550 |
| Board density, ρ [kg/m3] | 458 | 464 |
| Axial frequency, fa1 [Hz] | 548 | 559 |
| Dynamic MOE, Edyn [GPa] | 11.4 | 12.0 |
| Pith location (y, z) [mm] 1 | (−3.5, 77.5) | (−7.5, 41.5) |
| Parameter | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Nominal values | 10,700 | 710 | 430 | 500 | 620 | 24 | 0.025 | 0.31 | 0.38 |
| Adjusted values | 10,700 µ | 710 µ | 430 µ | 500 µ | 620 µ | 24 µ | 0.025 | 0.31 | 0.38 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, M.; Olsson, A.; Johansson, M.; Oscarsson, J. Modelling Local Bending Stiffness of Norway Spruce Sawn Timber Using Scanned Fibre Orientation. Proceedings 2018, 2, 505. https://doi.org/10.3390/ICEM18-05426
Hu M, Olsson A, Johansson M, Oscarsson J. Modelling Local Bending Stiffness of Norway Spruce Sawn Timber Using Scanned Fibre Orientation. Proceedings. 2018; 2(8):505. https://doi.org/10.3390/ICEM18-05426
Chicago/Turabian StyleHu, Min, Anders Olsson, Marie Johansson, and Jan Oscarsson. 2018. "Modelling Local Bending Stiffness of Norway Spruce Sawn Timber Using Scanned Fibre Orientation" Proceedings 2, no. 8: 505. https://doi.org/10.3390/ICEM18-05426
APA StyleHu, M., Olsson, A., Johansson, M., & Oscarsson, J. (2018). Modelling Local Bending Stiffness of Norway Spruce Sawn Timber Using Scanned Fibre Orientation. Proceedings, 2(8), 505. https://doi.org/10.3390/ICEM18-05426




