Numerical Investigations on the Fatigue Life of Lean Duplex Transverse Stiffeners in Bridges †
Abstract
:1. Fatigue Behavior of Stainless Steel Welded Details
1.1. General Introduction
1.2. The Hot Spot Stress Method
2. Design and Fabrication of the Tested Sample
2.1. Design Based on FE Sensitivity Analysis
2.2. Fabrication and Welding Parameters
3. Experimental Determination of the Hot Spot Stress
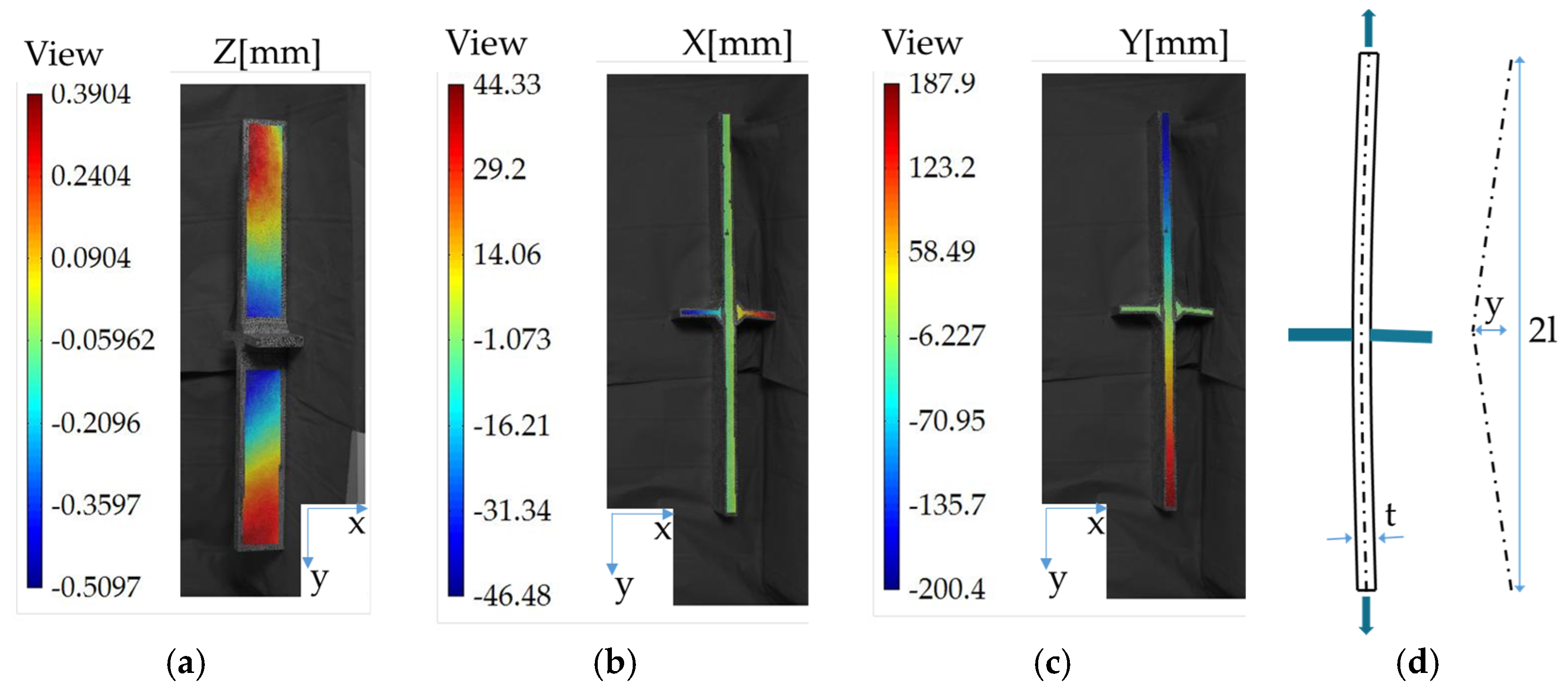
3.1. Test Arrangement and Geometric Imperfection
3.2. Comparison of the Measured and Computed Hot Spot Stress
3.3. Fatigue Strength Modification Factor Due to Misalignment (km)
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Wei, Z.; Laizhu, J.; Jincheng, H.; Hongmei, S. Study of mechanical and corrosion properties of a Fe-21.4Cr-6Mn-1.5Ni-0.24N-0.6Mo duplex stainless steel. Mater. Sci. Eng. 2008, 497, 501–504. [Google Scholar] [CrossRef]
- Lukić, M.; Al-Emrani, M.; Aygül, M.; Bokesjö, M.; Urushadze, S.; Frýba, L.; Škaloud, M.; Collin, P.; Nilsson, M.; Eichler, B.; et al. Bridge Fatigue Guidance—Meeting Sustainable Design and Assessment (BRiFaG); Research Fund for Coal and Steel (RFCS): Brussels, Belgium, 2013. [Google Scholar]
- Pedro, J.O.; Reis, A.; Baptista, C. High strength steel (HSS) S690 in highway bridges: Comparative design. In Proceedings of the Eurosteel, Copenhagen, Denmark, 13–15 September 2017. [Google Scholar]
- Karabulut, B.; Lombaert, G.; Debruyne, D.; Rossi, B. Optimized design and life cycle cost analysis of a duplex welded girder bridge. In Proceedings of the International Symposium on Life-Cycle Civil Engineering, Ghent, Belgium, 28–31 October 2018. [Google Scholar]
- Hobbacher, A.F. Recommendations for Fatigue Design of Welded Joints and Components, 2nd ed.; International Institute of Welding (IIW): Paris, France, 2016. [Google Scholar]
- Zilli, G.; Maiorana, E.; Peultier, J.; Fanica, A.; Hechler, O.; Rauert, T. Application of Duplex Stainless Steel for Welded Bridge Construction (BRIDGEPLEX); Research Fund & Coal and Steel (RFCS): Brussels, Belgium, 2008. [Google Scholar]
- Fricke, W. Fatigue analysis of welded joints: State of development. Mar. Struct. 2003, 16, 185–200. [Google Scholar] [CrossRef]
- Niemi, E.; Fricke, W.; Maddox, S.J. Fatigue Analysis of Welded Components: Designer’s Guide to the Structural Hot Spot Stress Approach, 2nd ed.; International Institute of Welding (IIW): Paris, France, 2018. [Google Scholar]
- Aygül, M.; Al-Emrani, M.; Urushadze; S. Modelling and fatigue life assessment of orthotropic bridge deck details using FEM. Int. J. Fatigue 2012, 40, 129–142. [Google Scholar] [CrossRef]
- Lee, J.; Seo, J.; Kim, M.; Shin, S.; Han, M.; Park, J. Comparison of hot spot stress evaluation methods for welded structures. Int. J. Nav. Archit. Ocean Eng. 2010, 2, 200–210. [Google Scholar] [CrossRef]
- Liu, R.; Liu, Y.; Ji, B.; Wang, M.; Tian, Y. Hot spot stress analysis on rib-deck welded joint in orthotropic steel decks. J. Constr. Steel Res. 2014, 97, 1–9. [Google Scholar] [CrossRef]
- Kotecki, D.J. Some pitfalls in welding of duplex stainless steels. Soldagem Inspeção 2010, 15, 336–343. [Google Scholar] [CrossRef]
- Fortan, M.; Dejans, A.; Debruyne, D.; Rossi, B. The strength of stainless steel fillet welds using GMAW. In Proceedings of the Stainless Steel in Structures: Fifth International Experts Seminar, London, UK, 18–19 September 2017. [Google Scholar]
- MatchID Software. Available online: http://www.matchidmbc.be (accessed on 8 April 2018).
- Poutiainen, I.; Tanskanen, P.; Marquis, G. Finite element methods for structural hot spot stress determination—A comparison of procedures. Int. J. Fatigue 2004, 26, 1147–1157. [Google Scholar] [CrossRef]




| Welding Zone | Ferrite Content (%) | Standard Deviation [2σ] | Suggested Ferrite Content [%] |
|---|---|---|---|
| B.M | 54 | 54 ± 7 | 40 to 60 |
| H.A.Z | 66 | 66 ± 8 | 25 to 75 |
| F.Z | 53.6 | 53.6 ± 8 | 25 to 60 (GMAW) |
| Hot spot Stress [σHS] | Linear [MPa] | Fatigue Life [N] | Comparison to the Experiment |
|---|---|---|---|
| Average experiment | 96.5 ± 4 1 | 2.2 × 106 | - |
| Numerical (theoretical FEM) | 85 | 3.3 × 106 | +3% |
| Modified SHSS (km,eff) | 96 | 2.3 × 106 | +0.1% |
| Modified SHSS (km,default) | 93 | 2.4 × 106 | +0.7% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karabulut, B.; Lombaert, G.; Debruyne, D.; Rossi, B. Numerical Investigations on the Fatigue Life of Lean Duplex Transverse Stiffeners in Bridges. Proceedings 2018, 2, 415. https://doi.org/10.3390/ICEM18-05278
Karabulut B, Lombaert G, Debruyne D, Rossi B. Numerical Investigations on the Fatigue Life of Lean Duplex Transverse Stiffeners in Bridges. Proceedings. 2018; 2(8):415. https://doi.org/10.3390/ICEM18-05278
Chicago/Turabian StyleKarabulut, Burak, Geert Lombaert, Dimitri Debruyne, and Barbara Rossi. 2018. "Numerical Investigations on the Fatigue Life of Lean Duplex Transverse Stiffeners in Bridges" Proceedings 2, no. 8: 415. https://doi.org/10.3390/ICEM18-05278
APA StyleKarabulut, B., Lombaert, G., Debruyne, D., & Rossi, B. (2018). Numerical Investigations on the Fatigue Life of Lean Duplex Transverse Stiffeners in Bridges. Proceedings, 2(8), 415. https://doi.org/10.3390/ICEM18-05278





