Biaxial Compression Tests on Hopkinson Bars †
Abstract
:1. Introduction
2. Hopkinson Bar Set-Up and Obtained Measurements
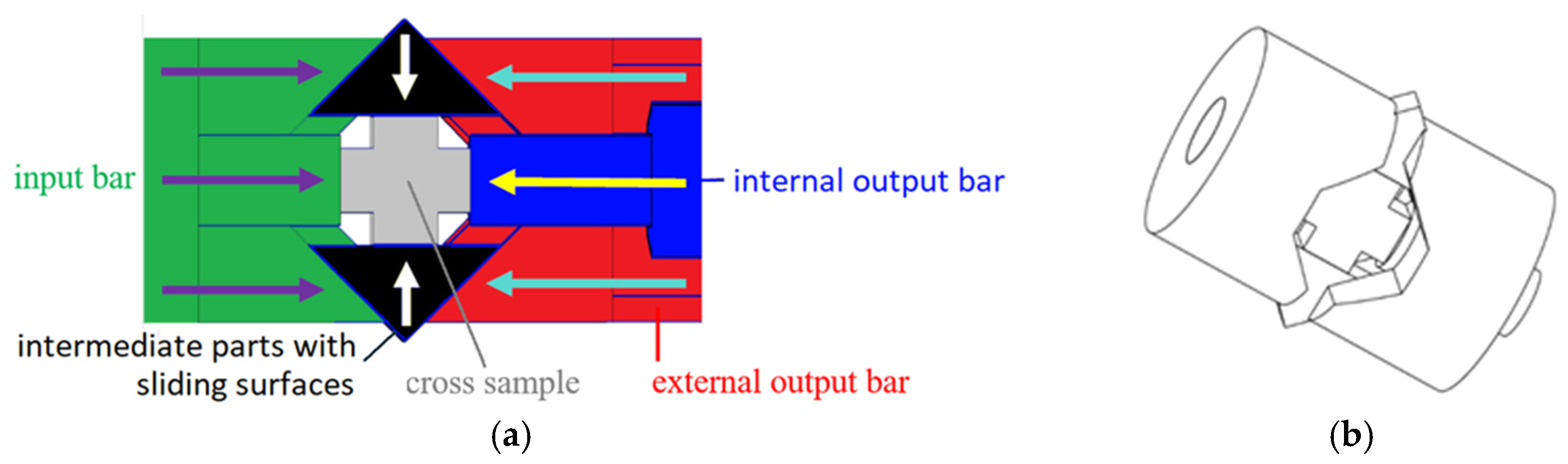
2.1. Set-Up Working and Characteristics
2.2. Forces and Velocities Measurements
2.3. Images Processing
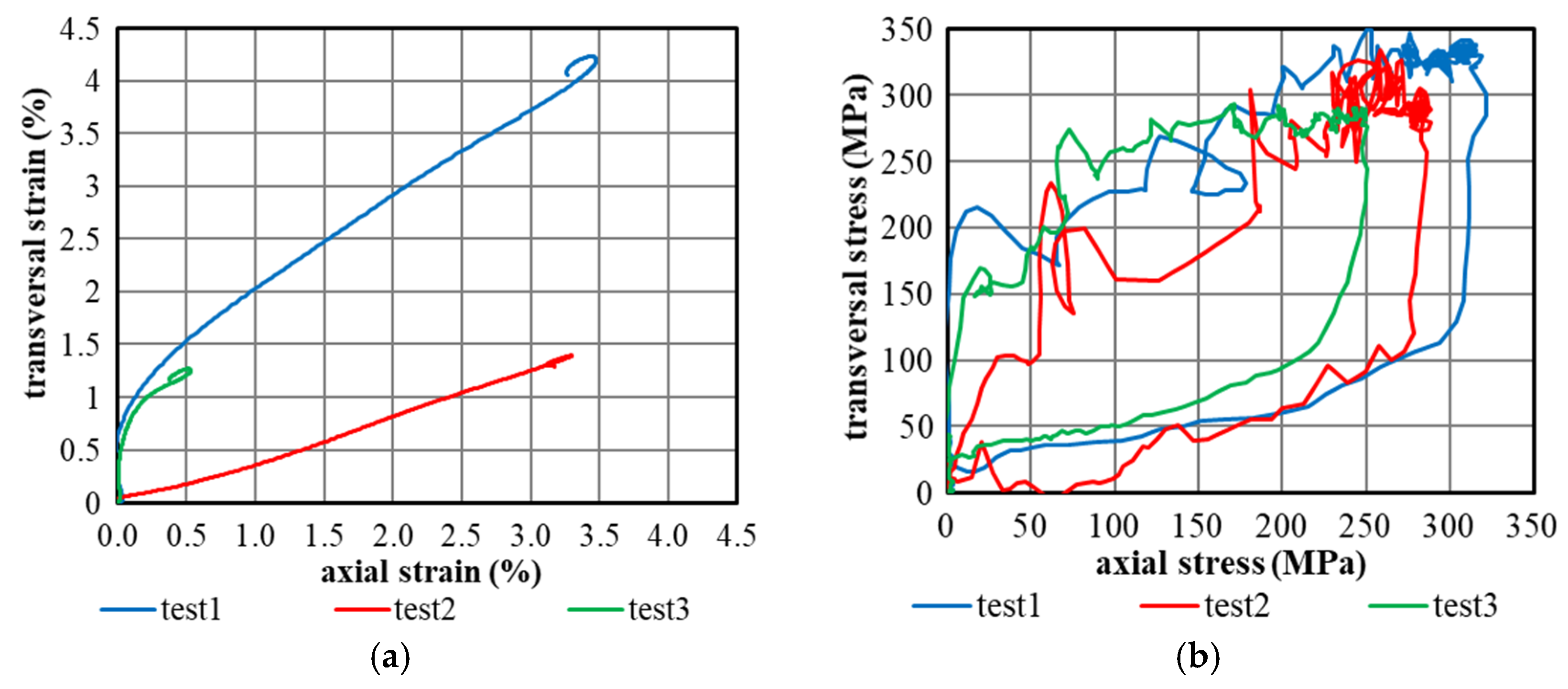
3. Experimental Results
3.1. Forces Equilibrium
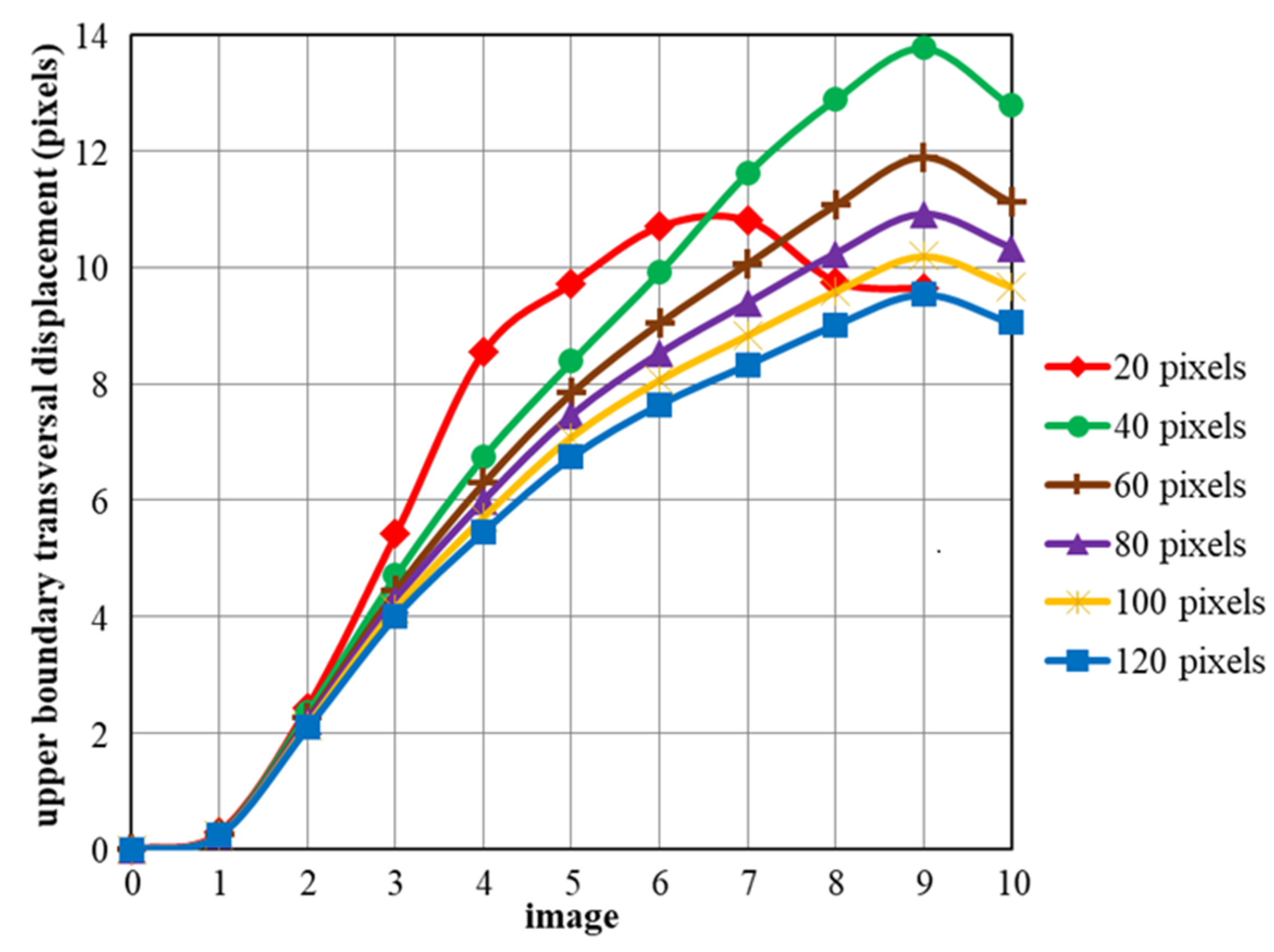
3.2. Images Processing
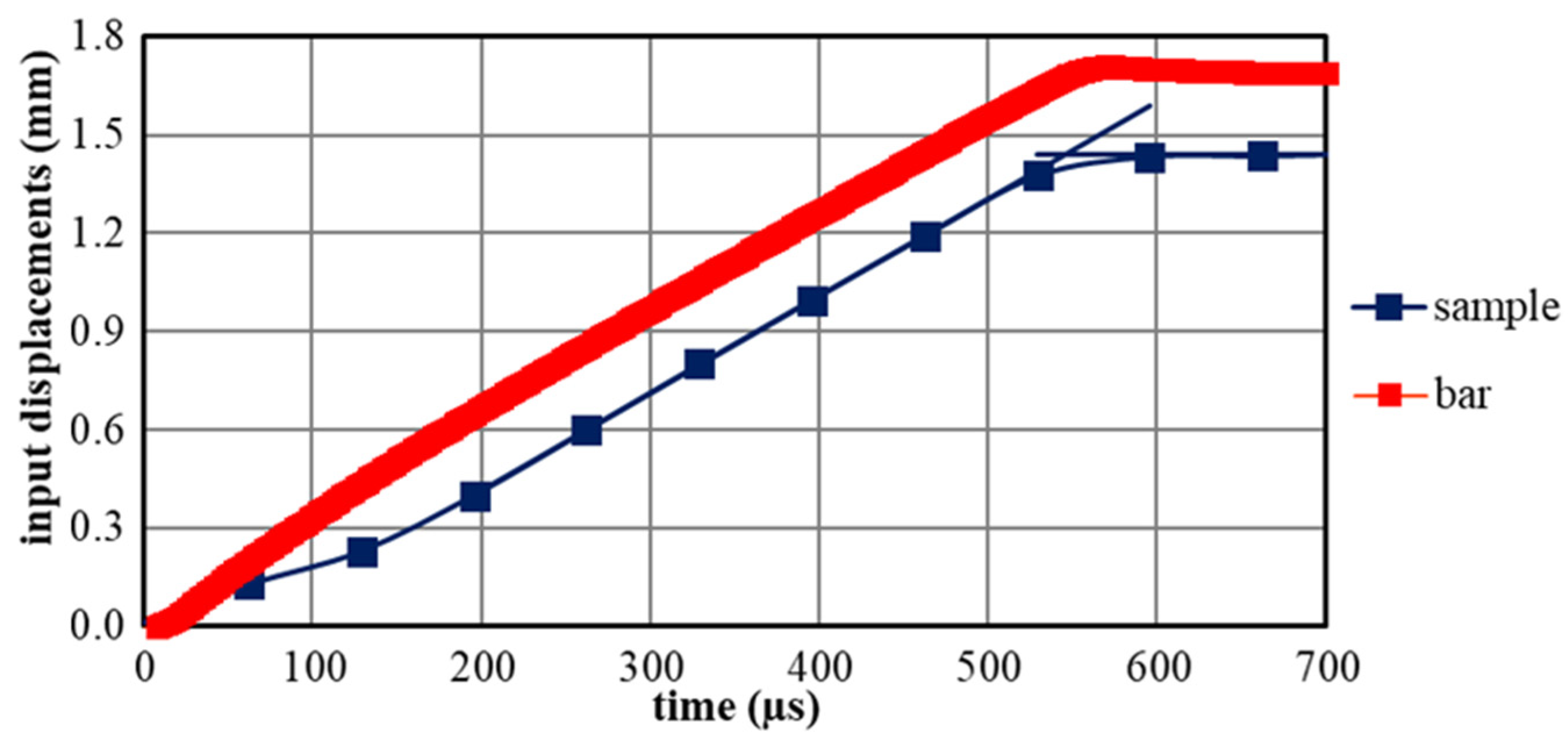
3.3. Time Shifting of the Images Relatively to the Gauges Signals
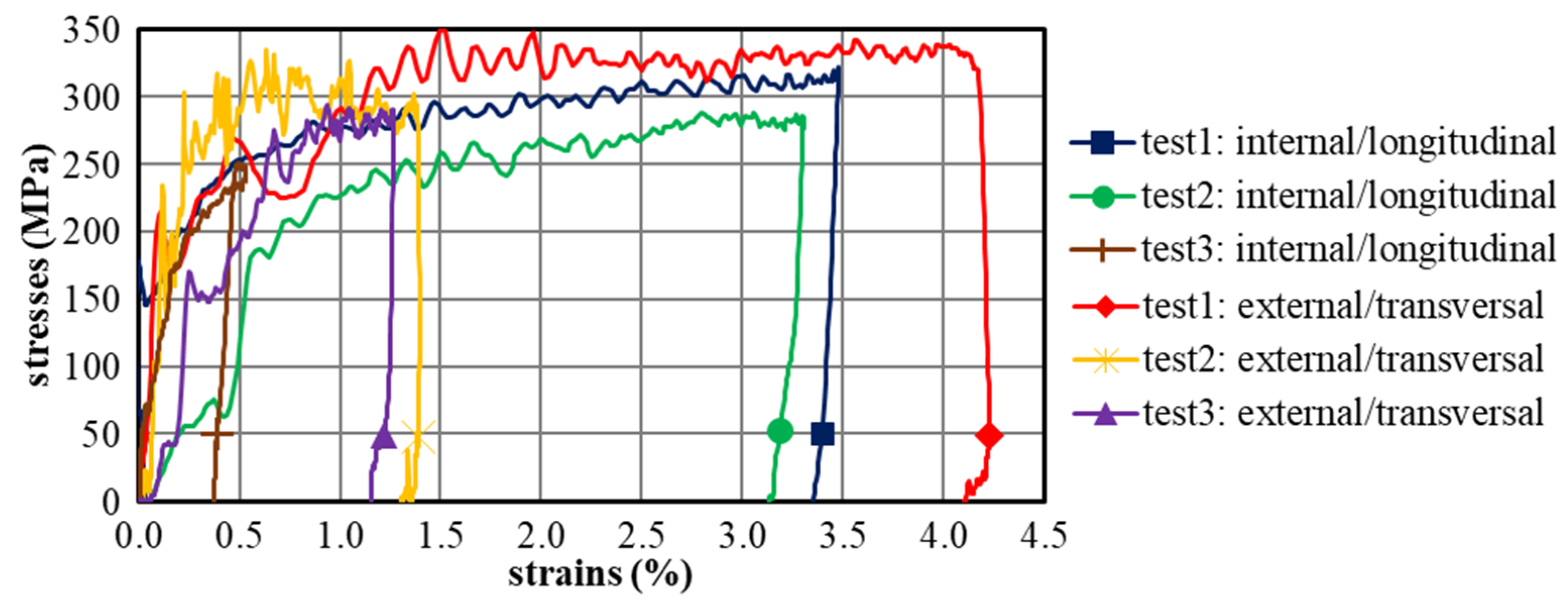
3.4. Stress and Strain State Reached during the Test
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Durrenberger, L. Analyse de la Pré-Déformation Plastique sur la Tenue au crash d’une Structure Crash-Box par Approches Expérimentale et Numérique. Ph.D Thesis, Paul Verlaine University of Metz, Metz, France, 2007. [Google Scholar]
- Albertini, C.; Cadoni, E.; Solomos, G. Advances in the Hopkinson bar testing of irradiated/non-irradiated nuclear materials and large specimens. Phil. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372, 2015. [Google Scholar] [CrossRef] [PubMed]
- Carlo Albertini, M.M. Dynamic Uniaxial and Biaxial Stress-Strain Relationships for Austenitic Stainless Steels. Nucl. Eng. Des. 1980, 57, 107–123. [Google Scholar] [CrossRef]
- Tomicevc, Z.; Hild, F.; Roux, S. Mechanics-aided digital image correlation. J. Strain Anal. 2013, 48, 330–343. [Google Scholar] [CrossRef]



| Bar | Density | Wave Celerity | Radius | Length | |
|---|---|---|---|---|---|
| External | Internal | ||||
| striker | ρi = 8050 kg·m−3 | Ci = 4600 m·s−1 | Ri = 11 mm | 1.25 m | |
| input | 4 m | ||||
| internal output | ρio = 7800 kg·m−3 | Cio = 5100 m·s−1 | Rio = 6 mm | 2 m | |
| external output | ρeo = 7400 kg·m−3 | Ceo = 5200 m·s−1 | Reeo = 11 mm | Rieo = 9 mm | 2 m |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Durand, B.; Zouari, A.; Zhao, H. Biaxial Compression Tests on Hopkinson Bars. Proceedings 2018, 2, 420. https://doi.org/10.3390/ICEM18-05263
Durand B, Zouari A, Zhao H. Biaxial Compression Tests on Hopkinson Bars. Proceedings. 2018; 2(8):420. https://doi.org/10.3390/ICEM18-05263
Chicago/Turabian StyleDurand, Bastien, Ahmed Zouari, and Han Zhao. 2018. "Biaxial Compression Tests on Hopkinson Bars" Proceedings 2, no. 8: 420. https://doi.org/10.3390/ICEM18-05263
APA StyleDurand, B., Zouari, A., & Zhao, H. (2018). Biaxial Compression Tests on Hopkinson Bars. Proceedings, 2(8), 420. https://doi.org/10.3390/ICEM18-05263




