Abstract
In this paper the potential application of experimental modal testing of railway bridges by application of the forced vibration excitation method is proposed to identify reliable and reproduceable values of the natural frequencies and damping coefficients. It will be shown, that the damping values that are determined by in-situ experimental modal testing are in most cases significant higher than the values given in EN 1991-2 and that the normative damping values are quite conservative. The measuring results of a framed concrete bridge with 16.1 m span length are presented and the dependence of dynamic parameters to seasonable temperature changes and to the size of bridge vibration amplitude will be discussed in detail.
1. Introduction
Railway bridges are excited to forced vibrations during train crossing and destabilization of the ballast bed may result. Thus, instability of the rail position may occur that lead to critical states for trains and passengers, respectively. During the design process of new railway bridges that are built on high-speed railway lines in European countries a dynamic analyses of train crossing must be performed and a limit value of 3.5 m/s2 of the maximum vertical bridge deck acceleration must be fulfilled according to EN 1991-2 [1]. A second limit value is the restriction of the bridge end rotations due to train crossing to a value of 6.7 ‰ according to the Austrian guideline “Dynamic calculation of railway bridges due to train crossing [2]”. In addition, the inertial force variables, i.e., bending moments and shear forces, due to train crossing must be smaller than the inertial forces that turn out from static analyses of bridge design.
The arising size of the bridges forced vibration amplitudes due to train crossing depends on both, train specific and bridge specific parameters. Train specific parameters represent the dynamic excitation forces and they are influenced of train speed, axle load and axle distances. The bridge specific parameters are essentially the natural frequencies and the structural damping coefficients. In cases, where the periodic excitation forces due to train crossing meets one of the natural frequencies of the bridge structure, resonant vibrations occur with unwanted large vibration amplitudes.
Within the dynamic analyses of train crossing the natural frequencies of railway bridges are computed on the basis of the ratio of bending stiffness to mass per unit length [3]. Both, the stiffness and the mass are taken from schemes of the bridge design documents If the boundary conditions are realistic defined in the analytical or numerical model, the comparison of calculated natural frequencies with frequencies determined by in-situ modal testing show a good agreement.
The structural damping of bridges is defined by the damping coefficient of Lehr and it cannot be calculated in practical applications. Within numerical simulations of train crossing the damping coefficients are always chosen according to regulations that are given in EN 1991-2. In case of steel and concrete bridges with span lengths L ≥ 20 m a value of 0.5% and of 1.5% has be chosen, respectively. In case of bridges with a smaller span length the damping can be increased by the factor 0.125 · (20 − L) in case of steel bridges and by 0.07 ⋅ (20 · L) in case of concrete bridges.
2. Research Project KOMET
2.1. Aim of the Project
The research project “KOMET” (funded by the Austrian Federal Railways, 2016—ongoing) carried out by the Austrian research company REVOTEC, the Austrian Institute of Technology (AIT) and the Vienna University of Technology aims to show the potential and the benefits of assessing dynamic parameters (natural frequencies and damping coefficients) of railway bridges and their non-linear behavior using modern forced vibration excitation methods. In addition, standard dynamic measurement methods are used and the results of gained natural frequencies and damping coefficients are compared, discussed and valuated in [4,5]. Another focus of the project is to improve the comparability of measurements carried out by different contractors by updating the current Austrian guideline “Dynamic measurements of railway bridges [6]”. A total of 50 railway bridges of different construction type have been measured since 2016 and the project is still ongoing. The span length of the bridges varies from 3 to 40 m and the measured natural frequencies (1st mode) varies from 3 to 80 Hz. As a main project result a table of realistic damping coefficients for railway bridges of different construction type is elaborated and recommendations for choosing the damping values within dynamic analyses of train crossing are specified.
2.2. Applied Experimental Modal Testing Methods
Within the Project KOMET in-situ experimental modal tests by application of the forced vibration excitation method were performed to identify the real values of natural frequencies and damping coefficients of different construction types of railway bridges. In addition, conventional dynamic measurement methods like ambient vibration measurement, time decay after train crossing and impact excitation through impulse hammer and sandbag are also applied to the tested railway bridges. The forced vibrations were mainly generated by use of two long stroke shakers in parallel operation, which are electrodynamic force generators, where the output is directly proportional to the instantaneous value of the applied current (see Figure 1).

Figure 1.
Electrodynamic long stroke shakers for experimental modal testing of railway bridges.
Both long stroke shakers are located, in dependence of the vibration mode of interest, on the railroad sleeper, on the ballast or on the boundary beam of the bridge. The moving mass of a single shaker is 30.6 kg and the dynamic excitation force is limited with 440 N. The long stroke shakers can deliver random or transient as well as sinusoidal waveforms of vertical excitation force in a very wide frequency range from 0.1 to 200 Hz. A closed-loop control is applied and assures a constant excitation force over the total frequency range of. The unit employs permanent magnets and is configured such that the armature coil remains in a uniform magnetic field over the entire stroke range—assuring force linearity. Within the performed bridge measurements, a sine-sweep signal was used to excite the railway bridges and the natural frequencies were identified in the time and the frequency domain. For determination of structural damping a manually sweep was performed within the frequency range of interest and the half power bandwidth method was applied.
In addition to the described electrodynamic long stroke vibration exciters a conventional unbalanced vibration exciter was also applied within a few selected dynamic measurements to study the influence of vibration amplitude size to the value of structural damping (see Figure 2). A maximum vertical dynamic excitation force of 175 kN can be generated over the frequency range from 1–25 Hz. The amount of excitation force is adjusted by proper choosing the number and size of rotating steel weights. The dynamic excitation force is a function of the rotating mass m, the eccentricity e and the excitation frequency Ω, defined by Pex (t) = m⋅e⋅Ω2⋅cosΩt, i.e., Pex,max = m⋅e⋅Ω2.

Figure 2.
Unbalanced vibration exciter for experimental modal testing of railway bridges.
The aim of the proposed forced vibration excitation method for experimental modal testing of railway bridges is beside the reliable determination of natural frequencies especially the reliable and reproducible determination of the structural damping coefficients, also by taking changing environmental conditions (temperature) and nonlinear effects (e.g., size of vibration amplitude) into account. In practice it is often observed, that the application of conventional monitoring methods for modal properties of structures, like ambient vibration monitoring show limits in the evaluation of realistic structural damping values. By use of the proposed forced vibration excitation method, significant vertical vibration amplitudes are generated and the values of structural damping result more realistic.
3. Experimental Modal Testing of a Framed Concrete Bridge
3.1. Identification of Natural Frequencies and Damping Coefficient under Summer Condition
The application of forced vibration excitation method for in-situ experimental modal testing of railway bridges is presented for a single span framed concrete railway bridge with ballast track. Two long stroke shakers in parallel operation and a conventional unbalanced vibration exciter (separate measurement) were used to excite the bridge to forced vibrations. The dynamic measurements were performed in summer (+16 °C) and in winter (−2 °C) condition. The bridge has two tracks and a span length of 16.10 m (see Figure 3). The bridge cross section consists of a 0.8 m thick continuous rectangular concrete plate without any longitudinal joint.
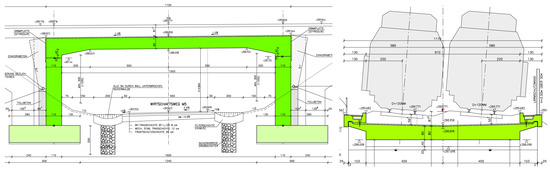
Figure 3.
Schemes of measured single span framed concrete railway bridge.
The two long stroke shakers (Figure 1) and the unbalanced vibration exciter (Figure 2, separate measurement) were positioned on the sleepers of a single track in the bridge midspan. The measurement equipment was placed below the bridge. Accelerometers were installed at different positions to measure the forced vibration response due to excitation by the long stroke shakers and by the unbalanced vibration exciter. To identify the natural frequencies of the framed concrete bridge, at first an automatic sine-sweep was conducted by use of the two long stroke shakers over the frequency range of interest from 5 to 50 Hz. The excitation force amplitude of the two shakers was chosen with F0,total = 433 N. The FFT of the generated acceleration time history indicates three dominant frequency peaks at f1 = 12.59 Hz, f2 = 16.57 Hz and at f3 = 33.13 Hz. These frequencies are the bending and torsional vibration modes of the bridge, respectively. The damping coefficient of Lehr ζ is determined for the relevant first vibration mode and therefore a manual sine-sweep with a total excitation force of F0,total = 866 N was performed (excitation force twice the force within the automatic sine sweep). Within the manual sweep the steady state bridge vibration was produced at every chosen excitation frequency and the maximum vibration amplitude response was recorded. The resulting frequency response function is shown in Figure 4 and the half power bandwidth method was applied to determine the damping coefficient of Lehr ζ.
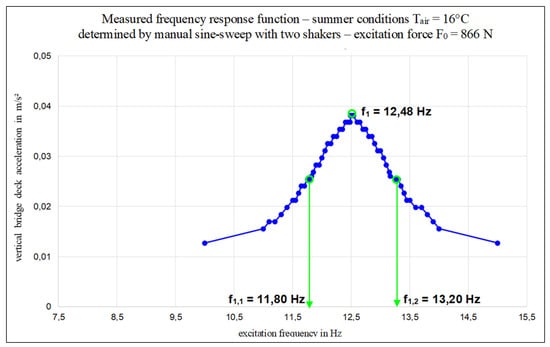
Figure 4.
Measured single span framed concrete bridge—frequency response function of bridge deck; manual sine-sweep by use of two long stroke shakers—summer conditions (+16 °C).
The results of the identified natural frequencies and of structural damping are given in Table 1 for both, the application of two long stroke shakers and the application of the unbalanced vibration exciter. It is seen that the measured structural damping coefficient of the first vibration mode is more than three times higher than the theoretical structural damping given in Eurocode ζEN1991-2 = 1.77%. The significant gap between in-situ measured structural damping coefficients and values given in European codes is detected in every measured framed concrete bridge.

Table 1.
Results of forced vibration excitation measurements by application of both, the two long stroke shakers in parallel operation and the unbalanced vibration exciter; summer conditions (+16 °C).
3.2. Identification of Natural Frequencies and Damping Coefficient under Winter Condition
To investigate the seasonable changes of dynamic bridge parameters a second dynamic measurement was performed under winter conditions (−2 °C). The position of the forced vibration excitation devices (two long stroke shakers and unbalanced vibration exciter) and of the accelerometers fixed to the bottom of the bridge deck was chosen according to the performed summer measurements. The FFT which was calculated from the acceleration time history results the three dominant frequencies with values f1 = 13.91 Hz, f2 = 19.09 Hz and f3 = 38.71 Hz. The structural damping coefficient was determined by application of the half power bandwidth method to the frequency response function generated by a manual sweep of the both long stroke shakers and a value of ζ1,winter = 6.52% results. The measured natural frequencies and structural damping under winter conditions are listed in Table 2 for both, the application of two long stroke shakers in parallel operation and the application of the unbalanced vibration exciter. It is indicated, that the increase of the first natural frequency from summer to winter results an amplification factor of 1.11 and of the structural damping coefficient of factor 1.16 and 1.26, respectively.

Table 2.
Results of forced vibration excitation measurements by application of both, the two long stroke shakers in parallel operation and the unbalanced vibration exciter; winter conditions (−2 °C).
3.3. Investigation of Nonlinear Damping Effects
To study the influence of the size of vibration amplitude to the resulting value of structural damping a series of manual sine-sweeps were performed over the frequency range of interest. Starting with a very low excitation force amplitude of Pex,1 = 0.90 kN by application of the two long stroke shakers in parallel operation, three additional excitation force levels were chosen Pex,2 = 6.58 kN, Pex,3 = 15.94 kN and Pex,4 = 20.81 kN by application of the unbalanced vibration exciter.
Figure 5 shows the frequency response function generated by a manual sine-sweep and every displayed curve indicates the response due to the specific chosen value of excitation force. It is seen that in case of application of the long stroke shakers a very small bridge amplitude in the range of 0.04 m/s2 occurs and that the corresponding damping coefficients results to 5.6%. The application of the unbalanced vibration exciter lead to maximum vibration amplitudes of 0.75 m/s2 and the corresponding damping coefficients results to 5.67%. It is concluded that the damping coefficient is independent from the amount of excitation force and bridge vibration amplitude, respectively.
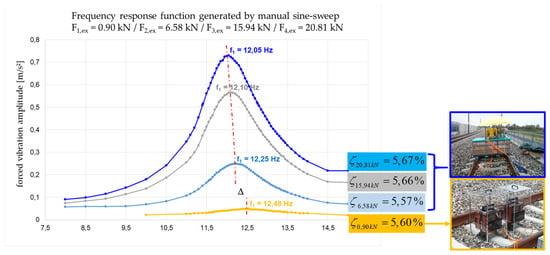
Figure 5.
RMS—Frequency response functions with different excitation forces (0.9 kN to 20.81 kN).
4. Conclusions
The performed work within the research project KOMET (50 railway bridges were under consideration) turn out, that the application of forced vibration excitation methods for experimental modal testing of railway bridges provides reliable and reproducible results for the natural frequencies and for the structural damping. Particularly, the structural damping coefficients that result from application of the half power bandwidth method to the frequency response function generated by manual sine-weeps with long stroke shakers, results in reliable and reproducible values as base for calibrating numerical simulations of train crossing. It is shown, that the in-situ measured structural damping coefficients of framed concrete railway bridges with ballast track are up to 4 times higher than the values given in European codes.
Author Contributions
M.R. conceived, designed and performed the in-situ tests of 30 railway bridges; M.R. performed the data analyzation of 30 railway bridges. M.R. wrote the paper. S.L. conceived, designed and performed the in-situ tests of 12 railway bridges; S.L. performed the data analyzation of 12 railway bridges. J.F. supplied scientific project support and he supported measurement design process. S.-Z.B.-A. supported the measurement design process.
Acknowledgments
The project KOMET was funded by the Austrian Federal Railways.
Conflicts of Interest
The authors declare no conflict of interest.
References
- ÖNORM EN 1991-2, Eurocode 1: Einwirkungen auf Tragwerke, Teil 2: Verkehrslasten auf Brücken (Ausgabe: 2012-03-01); Austrian Standard Institute: Vienna, Austria, 2012.
- Guideline. Dynamic Calculation Dynamic Calculation of Railway Bridges Due to Train Crossing; Austrian Federal Railways: Vienna, Austria, 2011. [Google Scholar]
- Petersen, C. Dynamic of Structures; Friedrich Vieweg & Sohn Verlagsgesellschaft mbH: Braunschweig/Wiesbaden, Germany, 1996; ISBN 3-528-08123-6. [Google Scholar]
- Reiterer, M.; Lachinger, S.; Fink, J.; Bruschetini-Ambro, S.-Z. Forced Vibration Monitoring of Railway Bridges by use of multiple long stroke shakers. In Proceedings of the 11th International Workshop on Structural Health Monitoring, Stanford, CA, USA, 12–14 September 2017. [Google Scholar]
- Reiterer, M.; Lachinger, S.; Fink, J.; Bruschetini-Ambro, S.-Z. Ermittlung der dynamischen Kennwerte von Eisenbahnbrücken mit unterschiedlichen Schwingungsanregungsmethoden. Bauingenieur 2017, 92, 2–13. [Google Scholar]
- Guideline. Dynamic Measurements of Railway Bridges; Austrian Federal Railways: Vienna, Austria, 2007. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).