Remote Sensing of Near-Real-Time Heavy Precipitation Using Observations from GPM and MFG over India and Nearby Oceanic Regions †
Abstract
:1. Introduction
2. Data Used and Study Area
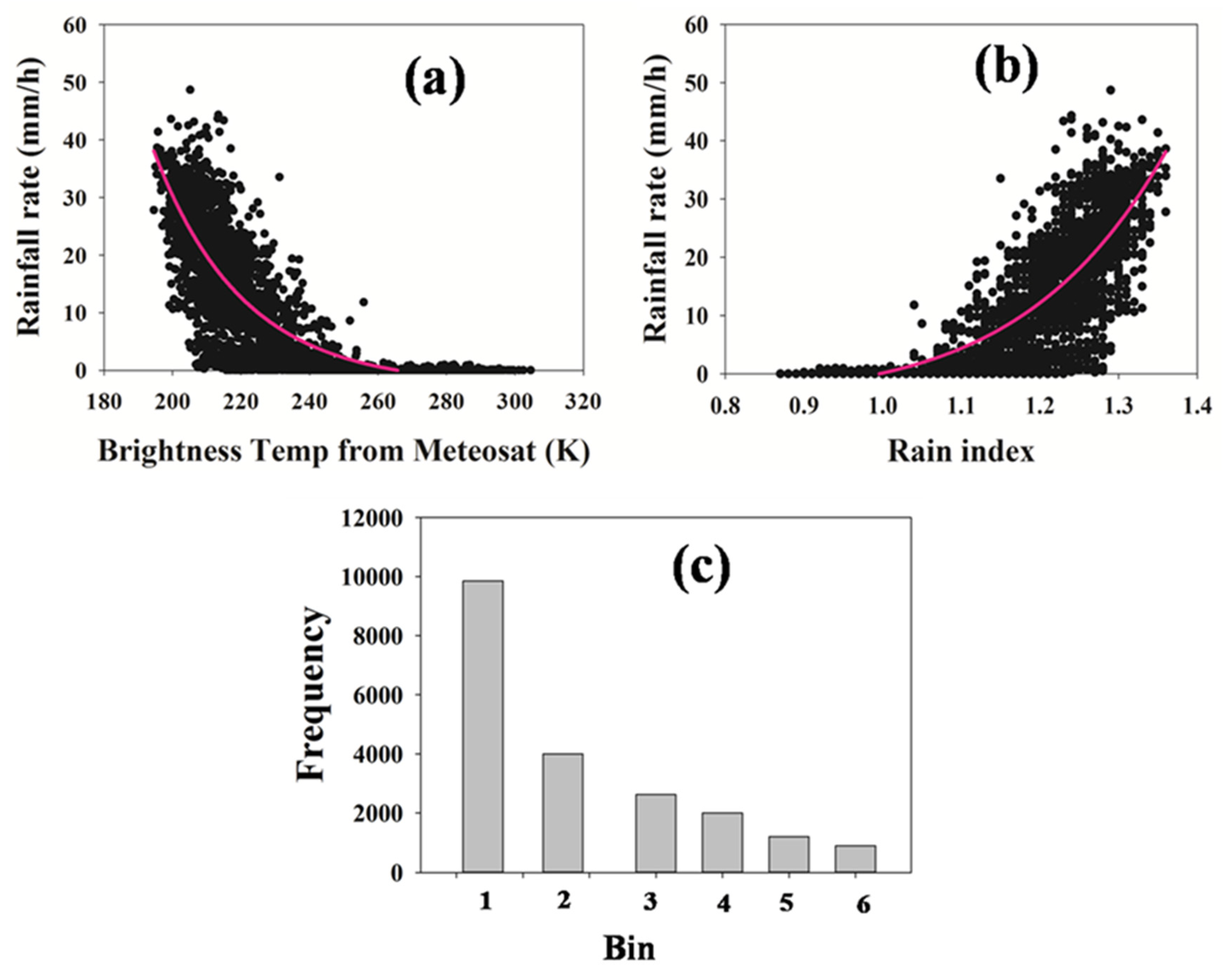
3. Methodology
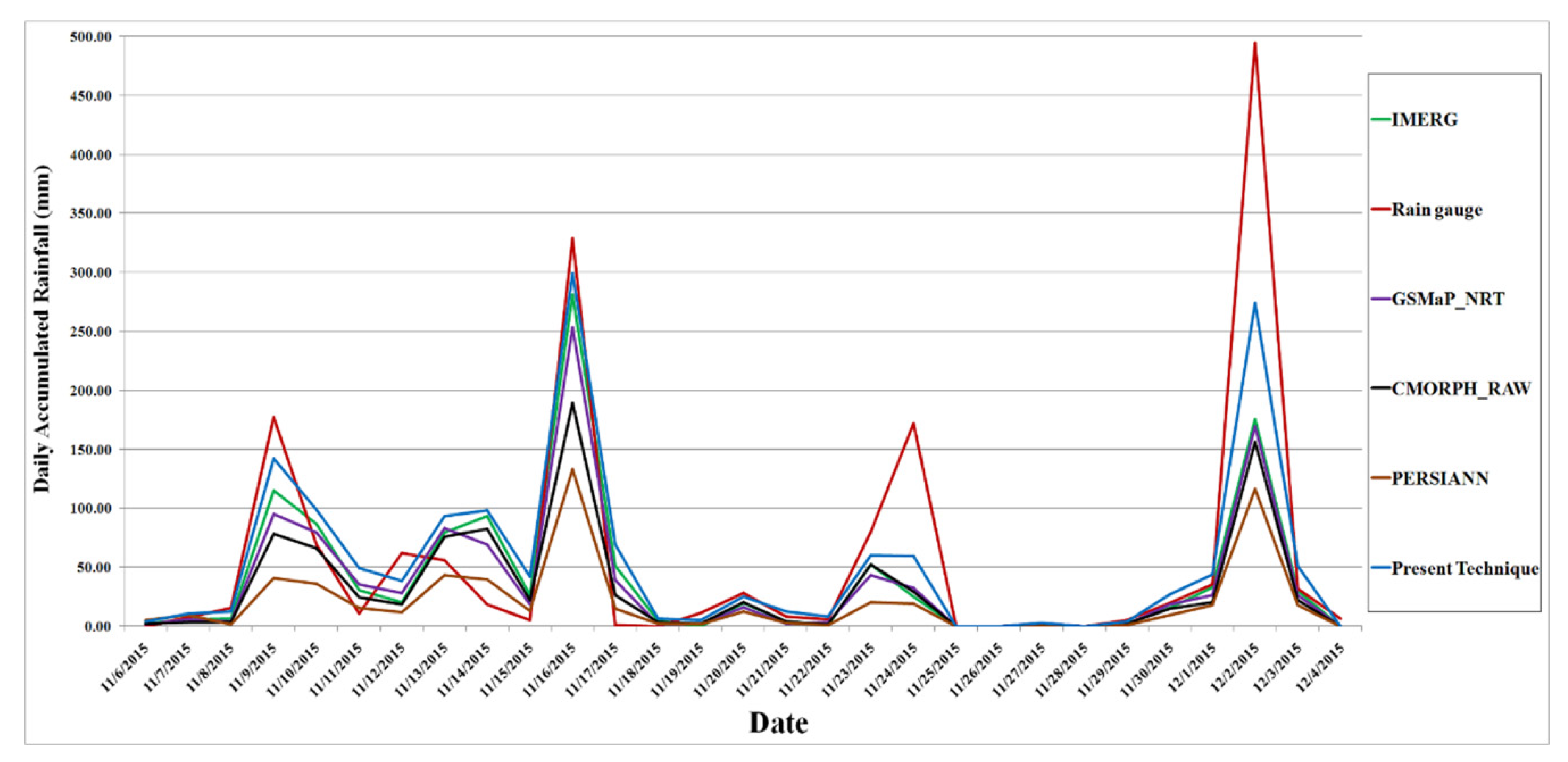
4. Results and Discussion
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Mishra, A. A study on the occurrence of flood events over Jammu and Kashmir during September 2014 using satellite remote sensing. Nat. Hazards 2015, 78, 1463–1467. [Google Scholar] [CrossRef]
- Mishra, A.; Srinivasan, J. Did a cloud burst occur in Kedarnath during 16 and 17 June 2013. Curr. Sci. 2013, 105, 1351–1352. [Google Scholar]
- Mishra, A.; Gairola, R.M.; Varma, A.K.; Agarwal, V.K. Remote sensing of Precipitation over Indian land and oceanic regions by synergistic use of multi-satellite sensors. J. Geophys. Res. 2010, 115, D08106. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G.; Nelkin, E.J.; Bowman, K.P.; Hong, Y.; Stocker, E.F.; Wolff, D.B. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Kubota, T.; Shige, S.; Hashizume, H.; Aonashi, A.; Takahashi, N.; Seto, S.; Hirose, M.; Takayabu, Y.N.; Ushio, T.; Nakagawa, K.; et al. Global precipitation map using satellite-borne microwave radiometers by the GSMaP project: Production and validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2259–2275. [Google Scholar] [CrossRef]
- Aonashi, K.; Awaka, J.; Hirose, M.; Kozu, T.; Kubota, T.; Liu, G.; Shige, S.; Kida, S.; Seto, S.; Takahashi, N.; et al. GSMaP passive microwave precipitation retrieval algorithm: Algorithm description and validation. J. Meteorol. Soc. Jpn. 2010, 87A, 119–136. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Hsu, K.L.; Gao, X.; Sorooshian, S.; Gupta, H.V. Precipitation estimation from remotely sensed information using artificial neural networks. J. Appl. Meteorol. Climatol. 1997, 36, 1176–1190. [Google Scholar] [CrossRef]
- Scofield, R.A.; Kuligowski, R.J. Status and outlook of operational satellite precipitation algorithms for extreme-precipitation events. Mon. Weather Rev. 2003, 18, 1037–1051. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Su, K.H.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Xie, P. NASA Global Precipitation Measurement (GPM) Integrated Multi-satellitE Retrievals for GPM (IMERG), Algorithm Theoretical Basis Document (ATBD) Version 4.5; Kidd, C., Nelkin, E.J., Eds.; NASA: Washington, DC, USA, 2015. Available online: https://pmm.nasa.gov/sites/default/files/document_files/IMERG_ATBD_V4.5_0.pdf (accessed on 2 February 2018).
- Mishra, A.; Gairola, R.M.; Varma, A.K.; Sarkar, A.; Agarwal, V.K. Rainfall Retrieval over Indian land and oceanic regions from SSM/I Microwave data. Adv. Space Res. 2009, 44, 815–823. [Google Scholar] [CrossRef]
- Mishra, A.; Gairola, R.M.; Varma, A.K.; Agarwal, V.K. Study of Intense Heavy Rainfall Events over India Using KALPANA-IR and TRMM- Precipitation Radar Observations. Curr. Sci. 2009, 9, 689–695. [Google Scholar]
- Mishra, A.; Gairola, R.M.; Agarwal, V.K. Rainfall Estimation from combined observations using KALPAANA-IR and TRMM-Precipitation Radar measurements over Indian Region. J. Indian Soc. Remote Sens. 2011, 40, 65–74. [Google Scholar] [CrossRef]
- Mishra, A.K. Monitoring Tamil Nadu flood of 2015 using satellite remote sensing. Nat. Hazards 2016, 82, 1431–1434. [Google Scholar] [CrossRef]
- Mishra, A.; Gairola, R.M.; Varma, A.K.; Agarwal, V.K. Improved rainfall estimation over Indian land oceanic regions using satellite infrared technique. Adv. Space Res. 2011, 48, 49–55. [Google Scholar] [CrossRef]
- Iguchi, T.; Kozu, T.; Kwiatkowski, J.; Meneghini, R.; Awaka, J.; Okamoto, K.I. Uncertainties in the Rain Profiling Algorithm for the TRMM Precipitation Radar. J. Meteorol. Soc. Jpn. 2009, 87, 1–30. [Google Scholar] [CrossRef]
- Grecu, M.; Olson, W.S.; Munchak, S.J.; Ringerud, S.; Liao, L.; Haddad, Z.; Kelley, B.L.; McLaughlin, S.F. The GPM Combined Algorithm. J. Atmos. Ocean. Technol. 2016, 33, 2225–2245. [Google Scholar] [CrossRef]
- Grecu, M.; Olson, W.S.; Shie, C.L.; L’Ecuyer, T.S.; Tao, W.K. Combining Satellite Microwave Radiometer and Radar observations to estimate atmospheric heating profiles. J. Clim. 2009, 22, 6356–6376. [Google Scholar] [CrossRef]
- Roca, R.; Viollier, M.; Picon, L.; Desbois, M. A multisatellite analysis of deep convection and its moist environment over the Indian Ocean during the winter monsoon. J. Geophys. Res. 2002, 107, INX2 11-1–INX2 11-25. [Google Scholar] [CrossRef]
- Rosenfeld, D.; Gutman, G. Retrieving microphysical properties near the tops of potential rain clouds by multispectral analysis of AVHRR data. Atmos. Res. 1994, 34, 259–283. [Google Scholar] [CrossRef]
- Adler, R.F.; Negri, A.J. A satellite infrared technique to estimate tropical convective and stratiform rainfall. J. Appl. Meteorol. 1988, 27, 30–51. [Google Scholar] [CrossRef]
- Laughlin, C.R. On the Effect of Temporal Sampling on the Observation of Mean Rainfall, Precipitation Measurements from Space; Work-Shop, Report; Atlas, D., Thiele, O.W., Eds.; NASA/Goddard Space Flight Cent.: Greenbelt, MD, USA, 1981; pp. 59–66. [Google Scholar]
- Mishra, A.; Rafiq, M. Towards combining GPM and MFG observations to monitor near real time heavy precipitation at fine scale over India and nearby oceanic regions. Dyn. Atmos. Oceans 2017, 80, 62–74. [Google Scholar] [CrossRef]
- Goswami, B.N.; Venugopal, V.; Sengupta, D.; Madhusoodanan, M.S.; Xavier, P.K. Increasing trend of extreme rain events over India in a warming environment. Science 2006, 314, 1442–1445. [Google Scholar] [CrossRef] [PubMed]
- Mishra, A.; Liu, S.C. Changes in precipitation pattern and risk of drought over India in the context of global warming. J. Geophys. Res. Atmos. 2014, 119, 7833–7841. [Google Scholar] [CrossRef]
- Mishra, A. A new technique to estimate precipitation at fine scale using multifrequency satellite observations over Indian land and oceanic regions. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4349–4358. [Google Scholar] [CrossRef]
- Mishra, A.K. Estimation of heavy rainfall during cyclonic storms from microwave observations using nonlinear approach over Indian Ocean. Nat. Hazards 2012, 63, 673–683. [Google Scholar] [CrossRef]
- Rafiq, M.; Mishra, A.K. A study of heavy snowfall in Kashmir, India in January 2017. Weather 2018, 73, 15–17. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rafiq, M.; Mishra, A.K. Remote Sensing of Near-Real-Time Heavy Precipitation Using Observations from GPM and MFG over India and Nearby Oceanic Regions. Proceedings 2018, 2, 327. https://doi.org/10.3390/ecrs-2-05140
Rafiq M, Mishra AK. Remote Sensing of Near-Real-Time Heavy Precipitation Using Observations from GPM and MFG over India and Nearby Oceanic Regions. Proceedings. 2018; 2(7):327. https://doi.org/10.3390/ecrs-2-05140
Chicago/Turabian StyleRafiq, Mohammd, and Anoop Kumar Mishra. 2018. "Remote Sensing of Near-Real-Time Heavy Precipitation Using Observations from GPM and MFG over India and Nearby Oceanic Regions" Proceedings 2, no. 7: 327. https://doi.org/10.3390/ecrs-2-05140
APA StyleRafiq, M., & Mishra, A. K. (2018). Remote Sensing of Near-Real-Time Heavy Precipitation Using Observations from GPM and MFG over India and Nearby Oceanic Regions. Proceedings, 2(7), 327. https://doi.org/10.3390/ecrs-2-05140





