Abstract
This paper deals with the development of a robust optimal control framework for a previously developed multi-body ski jumper simulation model by the authors. This framework is used to model uncertainties acting on the jumper during his jump, e.g., wind or mass, to enhance the performance, but also to increase the fairness and safety of the competition. For the uncertainty modeling the method of generalized polynomial chaos together with the discrete expansion by stochastic collocation is applied: This methodology offers a very flexible framework to model multiple uncertainties using a small number of required optimizations to calculate an uncertain trajectory. The results are then compared to the results of the Latin-Hypercube sampling method to show the correctness of the applied methods. Finally, the results are examined with respect to two major metrics: First, the influence of the uncertainties on the jumper, his positioning with respect to the air, and his maximal achievable flight distance are examined. Then, the results are used in a further step to quantify the safety of the jumper.
1. Introduction
In today’s high-performance sports, the competition level increases steadily requiring the coaches to instruct their athletes with more sophisticated training methods to help them best their opponents. Especially in ski jumping, which is in the scope of this research, the competition level is high, while the possibility for mistakes that can be corrected by the athlete is minimal. As additionally the chances for training sessions is rather limited, the conduction of simulations becomes of paramount importance for the training of the athletes [1].
Normally, a simulation can merely provide a reproduction of the already known results with some limited possibilities for an influence analysis. Therefore, an increasing interest is shifted in the direction of optimal control (OC) of the ski jumper’s posture, because OC provides methods for influence quantification. Here, different levels of fidelity are used: A rather low fidelity point-mass representation of a ski jumper in the longitudinal plane is looked at in [2]. The authors use an indirect optimization method by the Hamiltonian and optimize the flight path to get the maximal jump length using different take-off velocities. Study [3] uses a rigid-body representation in the longitudinal plane to optimize the jump length. The study sets up a direct OC problem defining a Nonlinear Programming Problem (NLP) and solve this numerically. Here, the influence of headwind and tailwind on the jumper’s performance is also considered.
The previous works show that current OC procedures for ski jumping mainly consider simple representations of the ski jumper and only a very limited amount of uncertainties, if at all. But, to give the jumper a detailed feedback on his performance and the possibilities to enhance it, a complex model as well as the uncertainties acting on him during the jump must be considered. Currently, this topic is of growing interest in the ski jumping community. The complex model will be a multi-body simulation (MBS) model, developed by the authors in a recent study [4]. The uncertainty modeling is based on the method of generalized polynomial chaos (gPC) [5]. gPC provides an analytic representation of the uncertainty influence on the optimal trajectory. Thus, it can be calculated a priori and can be evaluated on the jumping hill in real time to give the athlete direct feedback on his jump and the possibilities to enhance his performance. These results will naturally only be a suboptimal representation, which can then be under further examination in an offline optimization. As for the OC itself, the paper will use the direct OC formulation and transcribe the problem into a NLP, which is solved using the MATLAB-based toolbox FALCON.m [6].
2. Theoretical Background
This section gives an overview on the theoretical background of this paper and develops the framework. Section 2.1 considers the modeling and Section 2.2 the OC formulation. The uncertainty framework with gPC and SC is introduced in Section 2.3 and Section 2.4 respectively.
2.1. Modeling
The model for the OC is based on a MBS representation of a ski jumper presented in [4]. The structure of the model that uses a feedforward-feedback nonlinear dynamic inversion (NDI) [7] controller as illustrated in Figure 1. Further details on the implementation can be found in [4].
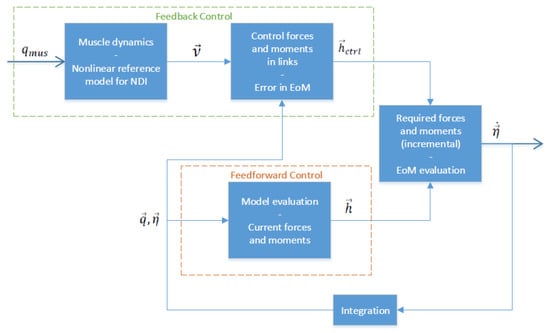
Figure 1.
Structure of feedforward-feedback NDI controller for the MBS ski jumper OC model [4].
We use a symmetric four-body representation of the ski jumper (torso, arm, leg, and ski) with the generalized coordinates:
and the generalized velocities:
Here, are the relative orientation angles (roll, pitch, yaw) between the bodies ( with origin ). The local earth frame is fixed on the take-off table (the x-axis points in hill direction, while the z-axis points up). The distances to the table are given by and with their velocities and respectively. The derivative of the first body angle is the pitch rate , while the other body angles are directly differentated with respect to time.
The initial values are:
These values correspond to the initial steady flight condition on Okurayama hill in Sapporo given in [3] (). Figure 2 illustrates the considered bodies and their movement directions.
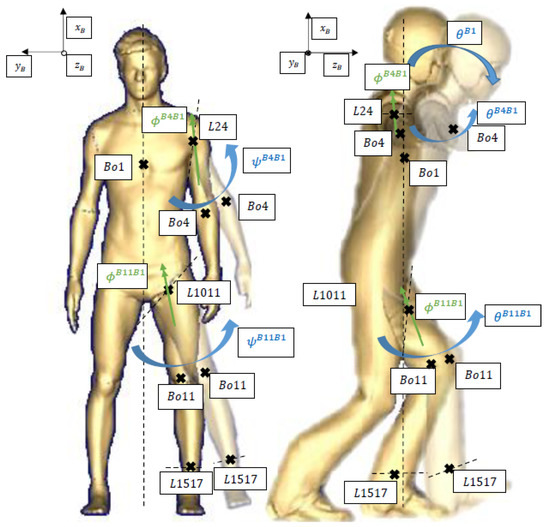
Figure 2.
MBS model of ski jumper with different bodies and movement directions and rotation axes [4].
2.2. Optimal Control
The trajectory optimization is done by means of direct OC. Therefore, the following OC problem is defined [8]:
In Equation (4), the cost functional is depicted by , including Mayer term and Lagrange term , the equality constraints are while the inequality constraints are . Additionally, the optimized trajectory must fulfill the state dynamics , which are represented by the MBS in this work (Section 2.1). These depend on the states (containing and ) and controls (containing the muscle activations ). The uncertain parameters are depicted by . The symbols and are the initial and final time respectively.
This continuous, infinite dimensional OC problem is transcribed by a full discretization direct OC approach into a NLP [8], which can then be used directly within off-the-shelf NLP solver such as IPOpt [9] (tolerances: ). This transcription and successive solution is supported by the Matlab-based toolbox FALCON.m, which was developed at the Institute of Flight System Dynamics of Technical University Munich [6].
2.3. Generalized Polynomial Chaos
The gPC method is a spectral representation of the uncertainties in random space [5]:
Equation (5) shows the decomposition of the uncertain problem into the uncertain parameters that are only related to the orthogonal polynomials and a deterministic part that is described by the expansion coefficients .
Here, the orthogonality relation defined for a scalar orthogonal polynomials is:
The uncertainty is defined by a probability density function (pdf) , which is given over the uncertainty region [5]. The normalizing constants are defined as and create an orthonormal polynomial. Orthonormal polynomials will be assumed throughout this work.
On the other hand, the expansion coefficients are defined by [5]:
The expansion coefficients are calculated by the SC approach introduced in the next paragraph.
2.4. Stochastic Collocation
The non-intrusive SC approach is used to calculate the gPC expansion coefficients. This method allows the sampling at deterministic nodes, as it uses a Gaussian quadrature rule to approximate the integral of Equation 7. The quadrature is based on the pdf of the uncertainty [5]:
In Equation (8), and are a set of Gaussian quadrature nodes and weights. The deterministic OC problem will be directly solved at these nodes, which allows a deterministic sampling.
3. Illustrative Example
This section introduces an illustrative example for the OC of the ski jumper considering uncertainties. We here use a normal distributed mass with a mean of and a standard deviation of . Figure 3a shows the optimized trajectory with the corresponding uncertainty bars around the mean value (solid red). We can observe that the change in mass significantly influences the jump length: For instance, we have a standard deviation of approximately in direction and in direction, which translates into a jump length change of approximately 0.9 m. Thus, a small weight change contributes to a rather significant change in the jumping length. Consequently, this makes up for a major influence in the safety of the athlete. On the other hand, Figure 3b depicts the comparison between gPC and Latin-Hypercube sampling (LHS) over a non-dimensional time . We can see that we get an accurate result from the gPC with only five samples compared to the LHS with 2000 samples. Thus, gPC shows both accuracy and efficiency.
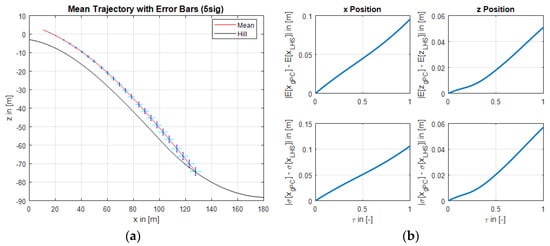
Figure 3.
Optimized trajectory with uncertainty bars (a) and absolute error between gPC solution and LHS over non-dimensional time for position (b) on Okurayama hill.
Now, Figure 4 depicts the development of the upper body angle and rate over the mean time. We can observe that the upper body angle (solid red) is not largely influenced by the uncertain mass, while the angular rate is quite largely influence by the uncertain mass. This yields the conclusion that the optimal posture of the upper body is independent of a varying mass. Therefore, the athlete needs to adapt differently with changing mass to uphold this optimal posture. Such results can be used to improve the performance of the athlete.
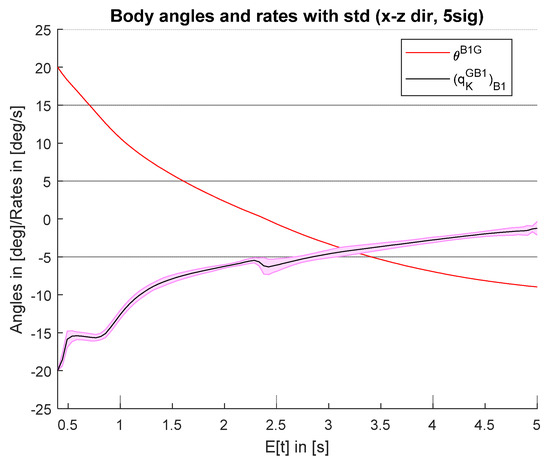
Figure 4.
Upper body angle and rate with uncertainty interval over mean jump time.
4. Conclusions and Perspective
This paper presented the OC under uncertainties of a MBS ski jumper model. The ski jumper was modeled using the constrained Newton-Euler equations combined with a NDI control law that shaped the movement of the jumper’s extremities to be physical. The framework used the Matlab-based OC toolbox FALCON.m combined with the gPC method for the quantification of the influences of uncertainties. By this, optimal trajectories could be generated that are stochastic, i.e., are defined by a mean and a standard deviation. This makes it to possible to get an insight into the jumper’s movement, e.g., when subject to a varying mass.
This can help athletes to adapt their flight style under different competitive conditions. Additionally, it can be used to show competition organizers, if the competition is still safe and fair. This can lead to a definition of the wind corridors and minimal mass, such that the maximal achievable jump length is still within the safe landing area. The results can also be used to define a suitable point metric for the evaluation of the jump in the sense of what could have been possible compared to what the jumper achieved. These evaluations can be carried out fast by the gPC expansion in a suboptimal way. Overall, the results can be used in the future to increase the fairness and safety in ski jumping competitions.
Although the presented results have already shown to be valid by comparing them to published results, they can still be enhanced by more sophisticated models. Additionally, more modeling techniques for uncertainty quantification such as chance constraints or bi-level OC should be considered.
Supplementary Materials
FALCON.m is available from www.falcon-m.com.
Acknowledgments
This research was supported by the Deutsche Forschungsgemeinschaft (DFG) through the TUM International Graduate School of Science and Engineering (IGSSE). The authors want to thank Veronica Bessone, Matthias Bittner, Xiang Fang, Benedikt Grüter, and Johannes Petrat for their support within the ski jumping project.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schwameder, H.; Müller, E. Biomechanics in ski jumping: A review. Eur. J. Sport Sci. 2001, 1, 1–16. [Google Scholar] [CrossRef]
- Jung, A.; Staat, M.; Müller, W. Optimization of the flight style in ski jumping. In Proceedings of the 11th World Congress on Computational Mechanics (WCCM XI), 5th European Conference on Computational Mechanics (ECCM V), 6th European Conference on Computational Fluid Dynamics (ECFD VI), Barcelona, Spain, 20–25 July 2014. [Google Scholar]
- Seo, K.; Murakami, M.; Yoshida, K. Optimal flight technique for V-style ski jumping. Sports Eng. 2004, 7, 97–103. [Google Scholar] [CrossRef]
- Piprek, P.; Glas, F.; Fang, X.; Bessone, V.; Petrat, J.; Bittner, M.; Holzapfel, F. Multi-Body Ski Jumper Model with Nonlinear Dynamic Inversion Muscle Control for Trajectory Optimization. Proceedings 2018, 321, 321. [Google Scholar] [CrossRef]
- Xiu, D. Numerical Methods for Stochastic Computations: A Spectral Method Approach; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Rieck, M.; Bittner, M.; Grüter, B.; Diepolder, J. Fast and Free Optimal Control for MATLAB®. Available online: http://www.fsd.mw.tum.de/software/falcon-m/ (accessed on 22 May 2016).
- Stevens, B.L.; Lewis, F.L. Aircraft Control and Simulation, 2nd ed.; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Betts, J.T. Practical Methods for Optimal Control and Estimation Using Nonlinear Programming, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2010. [Google Scholar]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).