Controlling Density and Modulus in Auxetic Foam Fabrications—Implications for Impact and Indentation Testing †
Abstract
:1. Introduction
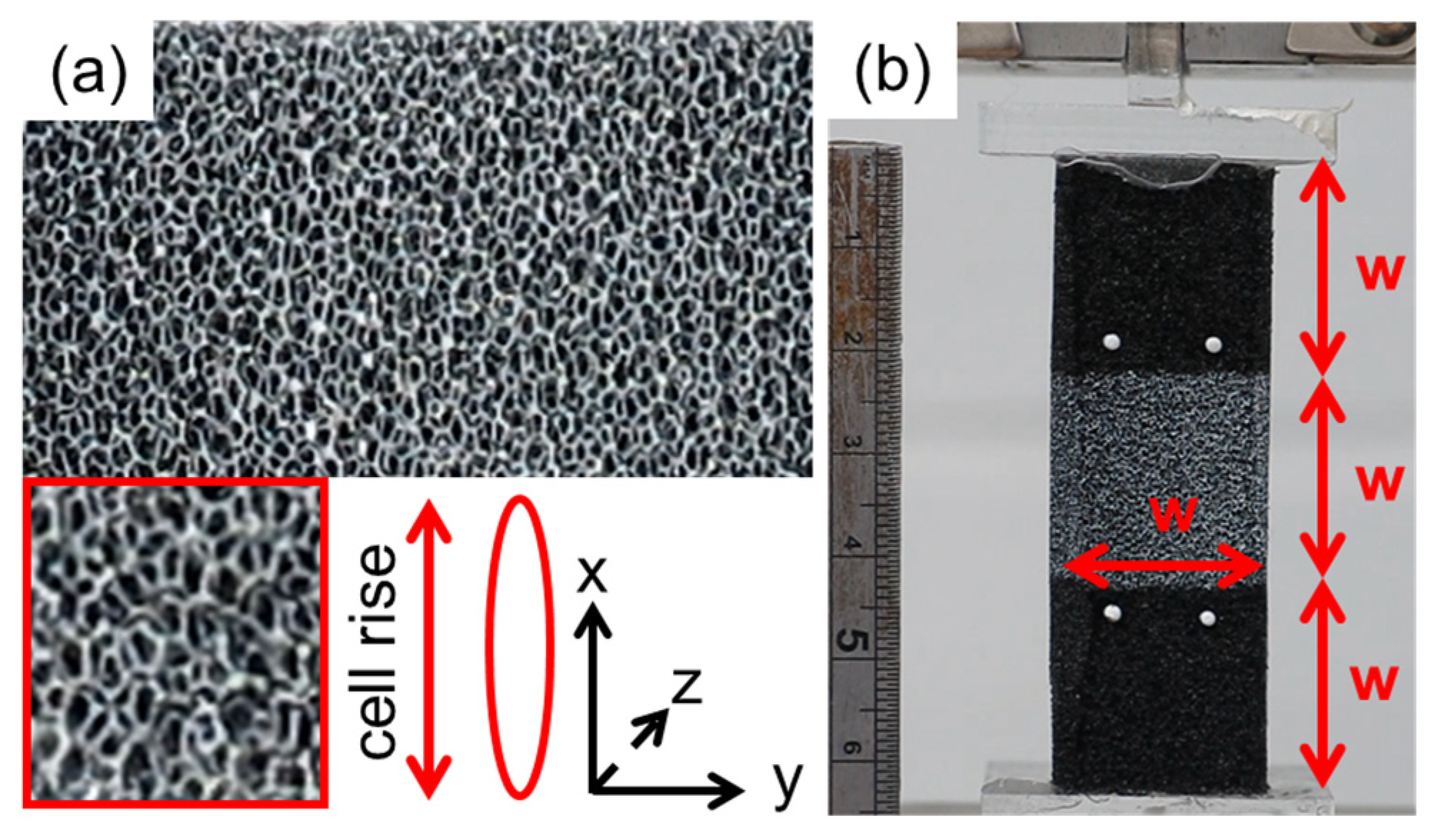
2. Materials and Methods
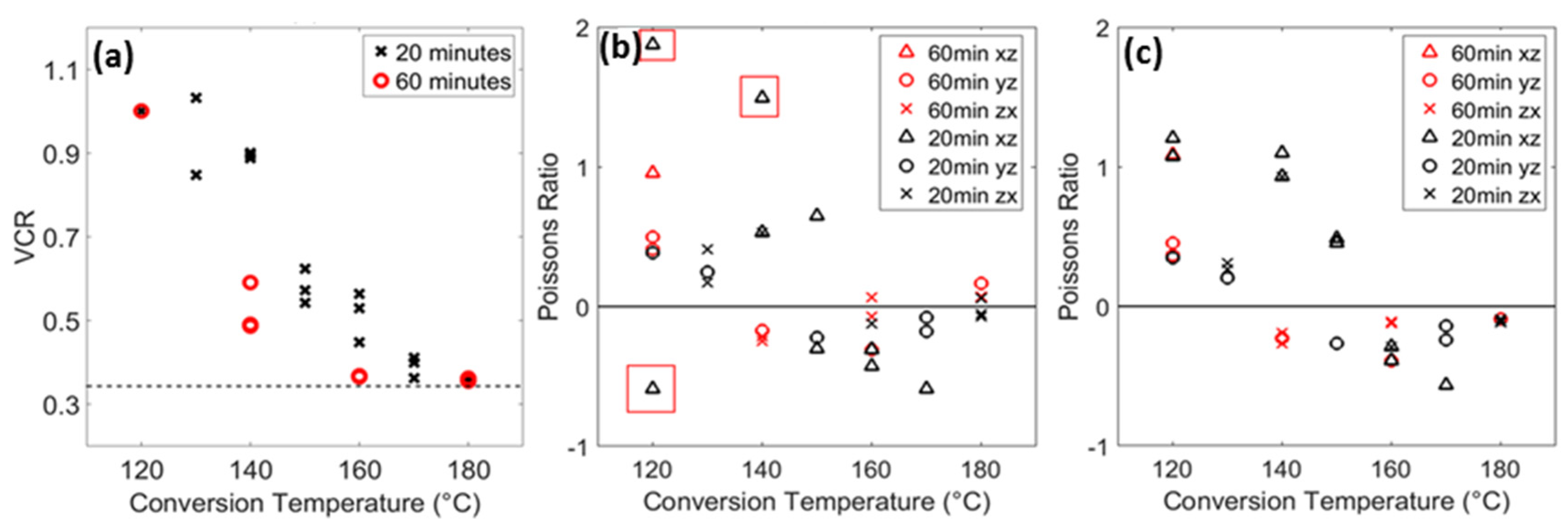
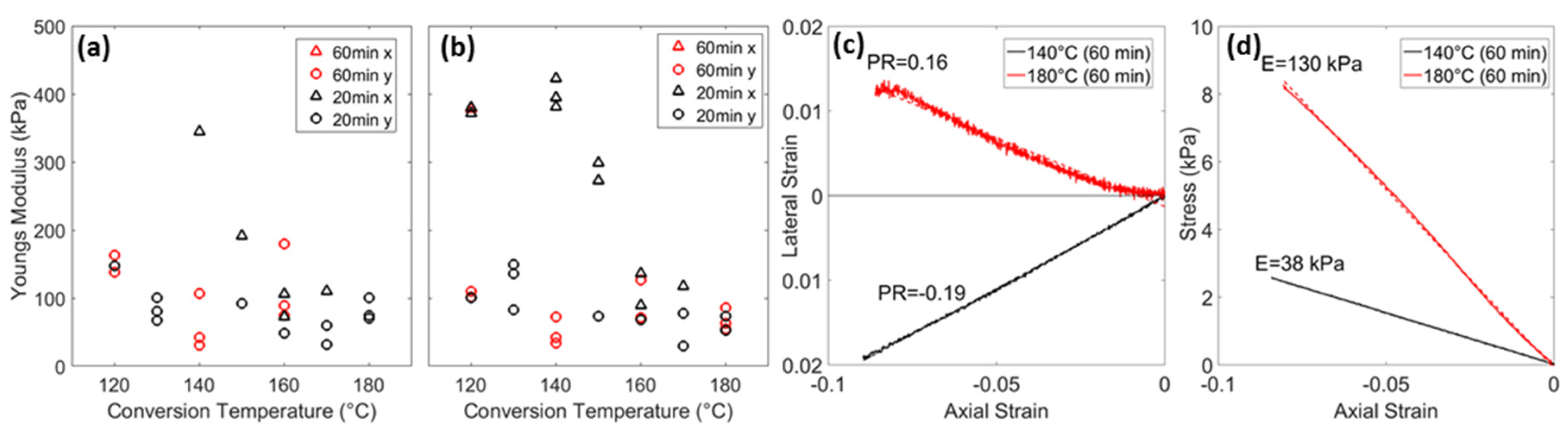
3. Results
4. Discussion
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Schmikli, S.; Backx, F.; Kemler, H.; Van Mechelen, W. National survey on sports injuries in the Netherlands: Target populations for sports injury prevention programs. Clin. J. Sport Med. 2009, 19, 101–106. [Google Scholar] [CrossRef] [PubMed]
- McIntosh, A. Biomechanical considerations in the design of equipment to prevent sports injury. Proc. Inst. Mech. Eng. 2012, 226, 193–199. [Google Scholar] [CrossRef]
- Payne, T.; Mitchell, S.; Halkon, B.; Bibb, R. A systematic approach to the characterisation of human impact injury scenarios in sport. BMJ Open Sport Exerc. Med. 2016, 2, 17. [Google Scholar] [CrossRef]
- Ankrah, S.; Mills, N.J. Performance of football shin guards for direct stud impacts. Sports Eng. 2003, 6, 207–219. [Google Scholar] [CrossRef]
- Ankrah, S.; Mills, N.J. Analysis of ankle protection in Association football. Sports Eng. 2009, 7, 41–52. [Google Scholar] [CrossRef]
- BSI. Protective Equipment for Cricketers; BS 6183-3:2000; BSI: London, UK, 2000. [Google Scholar]
- Adams, C.; James, D.; Senior, T.; Allen, T.; Hamilton, N. Development of a method for measuring quasi-static stiffness of snowboard wrist protectors. Procedia Eng. 2016, 147, 378–383. [Google Scholar] [CrossRef]
- ASTM F 2040-02. Standard Specification for Helmets Used for Recreational Snow Sports; ASTM International: West Conshohocken, PA, USA, 2011. [Google Scholar]
- CEN. Helmets for Alpine Skiers and Snowboarders; EN 1077:2007; CEN: Brussels, Belgium, 2007. [Google Scholar]
- McIntosh, A.; Andersen, T.; Bahr, R.; Greenwald, R.; Kleiven, S.; Turner, M.; Varese, M.; McCrory, P. Sports helmets now and in the future. Br. J. Sports Med. 2011, 45, 1258–1265. [Google Scholar] [CrossRef]
- Dickson, T.; Trathen, S.; Terwiel, F.; Waddington, G.; Adams, R. Head injury trends and helmet use in skiers and snowboarders in Western Canada, 2008–2009 to 2012–2013: An ecological study. Scand. J. Med. Sci. Sports 2017, 27, 236–244. [Google Scholar] [CrossRef]
- Ekeland, A.; Rødven, A.; Heir, S. Injury Trends in Recreational Skiers and Boarders in the 16-Year Period 1996–2012. In Snow Sports Trauma and Safety; Springer: Cham, Switzerland, 2017; pp. 3–16. [Google Scholar]
- Ferguson, J. Impact Shock Absorbing Material. U.S. Patent 8,087,101, 3 January 2012. [Google Scholar]
- Halldin, P. Helmet. U.S. Patent 8,578,520, 12 November 2013. [Google Scholar]
- Evans, K.; Nkansah, M.; Hutchinson, I.; Rogers, S. Molecular network design. Nature 1991, 353, 124–125. [Google Scholar] [CrossRef]
- Allen, T.; Duncan, O.; Foster, L.; Senior, T.; Zampieri, D.; Edeh, V.; Alderson, A. Auxetic Foam for Snow-Sport Safety Devices. In Snow Sports Trauma and Safety; Springer: Cham, Switzerland, 2017; pp. 145–159. [Google Scholar]
- Duncan, O.; Foster, L.; Senior, T.; Allen, T.; Alderson, A. A comparison of novel and conventional fabrication methods for auxetic foams for sports safety applications. Procedia Eng. 2016, 147, 384–389. [Google Scholar] [CrossRef]
- Evans, K.; Alderson, A. Auxetic materials: Functional materials and structures from lateral thinking! Adv. Mater. 2000, 12, 617–628. [Google Scholar] [CrossRef]
- Lakes, R. Foam structures with a negative Poisson’s ratio. Science 1987, 235, 1038–1041. [Google Scholar] [CrossRef] [PubMed]
- Ge, C. A comparative study between felted and triaxial compressed polymer foams on cushion performance. J. Cell. Plast. 2013, 49, 521–533. [Google Scholar] [CrossRef]
- Allen, T.; Shepherd, J.; Hewage, T.; Senior, T.; Foster, L.; Alderson, A. Low-kinetic energy impact response of auxetic and conventional open-cell polyurethane foams. Phys. Status Solidi B 2015, 252, 1631–1639. [Google Scholar] [CrossRef]
- Duncan, O.; Foster, L.; Senior, T.; Alderson, T.; Allen, T. Quasi-static characterisation and impact testing of auxetic foam for sports safety applications. Smart Mater. Struct. 2016, 25, 054014. [Google Scholar] [CrossRef]
- Gibson, L.; Ashby, M. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Choi, J.B.; Lakes, R.S. Non-linear properties of polymer cellular materials with a negative Poisson’s ratio. J. Mater. Sci. 1992, 27, 4678–4684. [Google Scholar] [CrossRef]
- Critchley, R.; Corni, I.; Wharton, J.; Walsh, F.; Wood, R.; Stokes, K. A review of the manufacture, mechanical properties and potential applications of auxetic foams. Phys. Status Solidi B 2013, 250, 1963–1982. [Google Scholar] [CrossRef]
- Bianchi, M.; Scarpa, F.; Smith, C. Shape memory behaviour in auxetic foams: Mechanical properties. Acta Mater. 2010, 58, 858–865. [Google Scholar] [CrossRef]
- Chan, N.; Evans, K. Fabrication methods for auxetic foams. J. Mater. Sci. 1997, 32, 5945–5953. [Google Scholar] [CrossRef]
- Chan, N.; Evans, K. Indentation resilience of conventional and auxetic foams. J. Cell. Plast. 1998, 34, 231–260. [Google Scholar] [CrossRef]
- Alderson, A.; Alderson, K.; Davies, P.; Smart, G. The effects of processing on the topology and mechanical properties of negative Poisson’s ratio foams. In Proceedings of the ASME 2005 International Mechanical Engineering Congress and Exposition, Orlando, FL, USA, 5–11 November 2005; pp. 503–510. [Google Scholar]
- Li, Y.; Zeng, C. On the successful fabrication of auxetic polyurethane foams: Materials requirement, processing strategy and conversion mechanism. Polymer 2016, 87, 98–107. [Google Scholar] [CrossRef]
- Duncan, O.; Allen, T.; Foster, L.; Senior, T.; Alderson, A. Fabrication, characterisation and modelling of uniform and gradient auxetic foam sheets. Acta Mater. 2017, 126, 426–437. [Google Scholar] [CrossRef]
- Boba, K.; Bianchi, M.; McCombe, G.; Gatt, R.; Griffin, A.C.; Richardson, R.M.; Scarpa, F.; Hamerton, I.; Grima, J.N. Blocked shape memory effect in negative Poisson’s ratio polymer metamaterials. ACS Appl. Mater. Interfaces 2016, 8, 20319–20328. [Google Scholar] [CrossRef] [PubMed]
- Allen, T.; Hewage, T.; Newton-Mann, C.; Shepherd, T.; Wang, W.; Duncan, O.; Alderson, A. Fabrication of auxetic foam sheets for sports applications. Phys. Status Solidi B 2017. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duncan, O.; Allen, T.; Foster, L.; Gatt, R.; Grima, J.N.; Alderson, A. Controlling Density and Modulus in Auxetic Foam Fabrications—Implications for Impact and Indentation Testing. Proceedings 2018, 2, 250. https://doi.org/10.3390/proceedings2060250
Duncan O, Allen T, Foster L, Gatt R, Grima JN, Alderson A. Controlling Density and Modulus in Auxetic Foam Fabrications—Implications for Impact and Indentation Testing. Proceedings. 2018; 2(6):250. https://doi.org/10.3390/proceedings2060250
Chicago/Turabian StyleDuncan, Olly, Tom Allen, Leon Foster, Ruben Gatt, Joseph N. Grima, and Andrew Alderson. 2018. "Controlling Density and Modulus in Auxetic Foam Fabrications—Implications for Impact and Indentation Testing" Proceedings 2, no. 6: 250. https://doi.org/10.3390/proceedings2060250
APA StyleDuncan, O., Allen, T., Foster, L., Gatt, R., Grima, J. N., & Alderson, A. (2018). Controlling Density and Modulus in Auxetic Foam Fabrications—Implications for Impact and Indentation Testing. Proceedings, 2(6), 250. https://doi.org/10.3390/proceedings2060250






