Effect of the Grip Angle on Off-Spin Bowling Performance Parameters, Analysed with a Smart Cricket Ball †
Abstract
1. Introduction
2. Material and Methods
2.1. Smart Cricket Ball
2.2. Participants
2.3. Performance Parameters
2.4. Data Analysis and Statistics
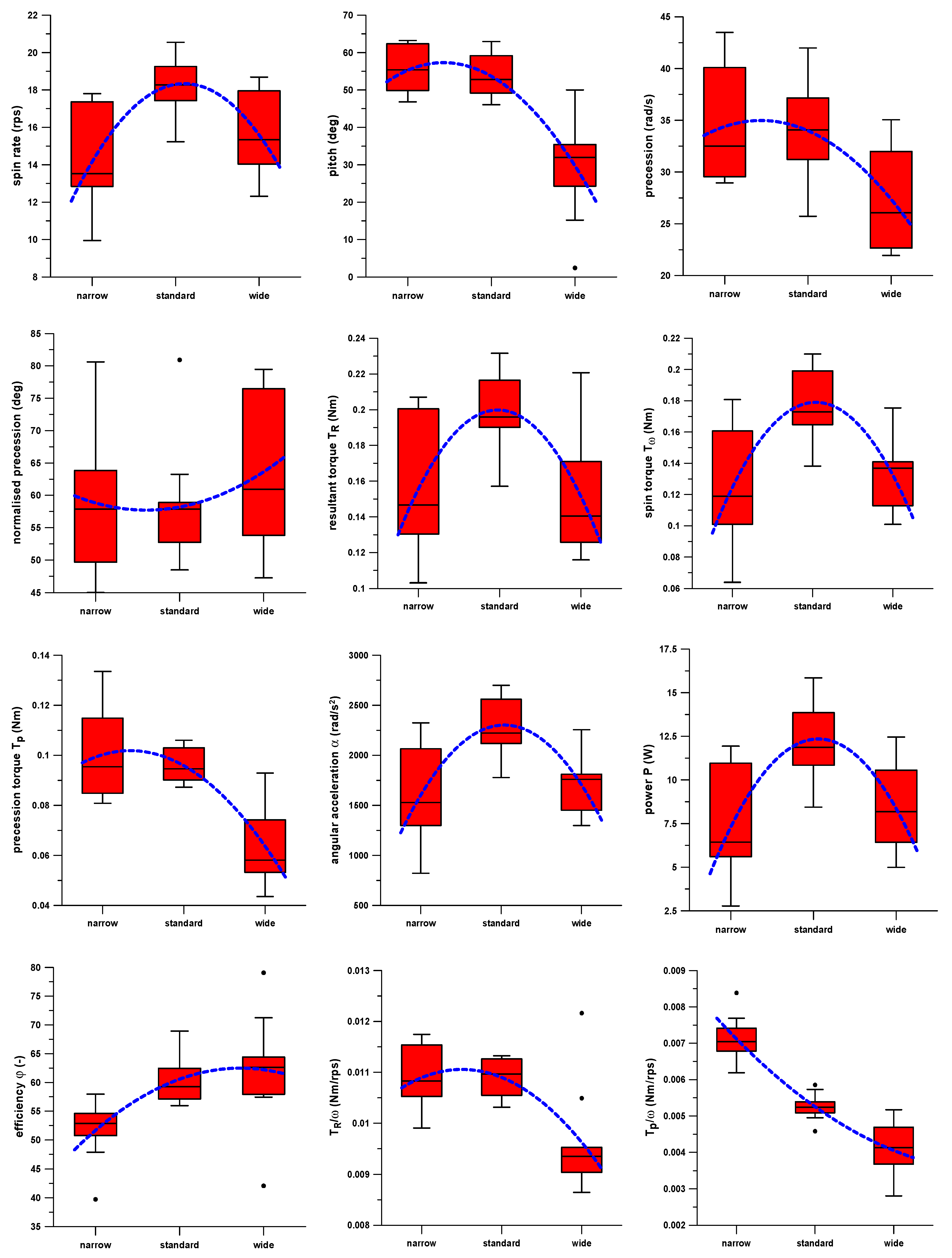
3. Results
- Optimum point (highest performance) at the standard grip and less performance at wide and narrow grips: standard grip performance was significantly higher compared to narrow and wide grips, with insignificant difference between wide and narrow grips. This trend was seen in the spin rate, resultant torque, spin torque, Tω/ω, peak angular acceleration, and peak power.
- Optimum point (highest performance) at the standard and narrow grips and less performance at the wide grip: standard and narrow grip performance was significantly higher compared to the wide grip, with insignificant difference between standard and narrow grips. This trend was seen in pitch and TR/ω.
- Optimum point (highest performance) at the standard and wide grips and less performance at the narrow grip: standard and wide grip performance was significantly higher compared to the narrow grip, with insignificant difference between standard and wide grips. This trend was seen in the efficiency.
- Optimum point (highest performance) at the wide grip and less performance at standard and narrow grips: the wide grip performance was significantly higher compared to standard and narrow grips, with insignificant difference between standard and narrow grips). This trend was seen in the precession and the precession torque.
- Optimum point (highest performance) at the wide grip and decreasing performance over standard to narrow grip: all 3 grip performances were significantly different. This trend was seen in Tp/ω.
- No trend at all (regression p > 0.05; ANOVA p > 0.05), seen in the normalized precession.
4. Discussion
Conflicts of Interest
References
- Fuss, F.K.; Doljin, B.; Ferdinands, R.E.D. Case studies of the centre of pressure between hand and ball in off-spin bowling, analysed with a smart cricket ball. Proc. Eng. 2016, 147, 203–207. [Google Scholar] [CrossRef][Green Version]
- Fuss, F.K.; Doljin, B.; Ferdinands, R.E.D.; Beach, A. Dynamics of spin bowling: The normalized precession of the spin axis analysed with a smart cricket ball. Proc. Eng. 2015, 112, 196–201. [Google Scholar]
- Fuss, F.K.; Lythgo, N.; Smith, R.M.; Benson, A.C.; Gordon, B. Identification of key performance parameters during off-spin bowling with a smart cricket ball. Sports Technol. 2011, 4, 159–163. [Google Scholar] [CrossRef]
- Fuss, F.K.; Smith, R.M. Should the finger pressure be well distributed across the seam in seam bowling? A problem of precession and torque. Proc. Eng. 2013, 60, 453–458. [Google Scholar] [CrossRef][Green Version]
- Fuss, F.K.; Smith, R.M. Accuracy performance parameters of seam bowling, measured with a smart cricket ball. Proc. Eng. 2014, 72, 435–440. [Google Scholar]
- Fuss, F.K.; Smith, R.M.; Subic, A. Determination of spin rate and axes with an instrumented cricket ball. Proc. Eng. 2012, 34, 128–133. [Google Scholar]
- Doljin, B.; Fuss, F.K. Development of a smart cricket ball for advanced performance analysis of bowling. Proc. Technol. 2015, 20, 133–137. [Google Scholar]
- Fuss, F.K.; Doljin, B.; Ferdinands, R.E.D. Unpublished data, 2017.

| Statistics | Regression R2 | Regression p | ANOVA p | Max Posthoc p: Narrow vs. Standard | Max Posthoc p: Narrow vs. Wide | Max Posthoc p: Standard vs. Wide | Narrow Grip (Mean ± Stdev) | Standard Grip (Mean ± Stdev) | Wide Grip (Mean ± Stdev) |
|---|---|---|---|---|---|---|---|---|---|
| ω (rps) | 0.4162 | 0.0001 | 0.0007 | 0.0010 | 0.4373 | 0.0305 | 14.16 ± 2.66 | 18.30 ± 1.53 | 15.60 ± 2.08 |
| pitch (°) | 0.6450 | <0.0001 | <0.0001 | 1.0000 | 0.0010 | 0.0010 | 55.26 ± 6.12 | 53.66 ± 5.97 | 29.73 ± 13.31 |
| max p (rad/s) | 0.2999 | 0.0017 | 0.0081 | 1.0000 | 0.0193 | 0.0284 | 34.39 ± 5.41 | 33.99 ± 5.02 | 27.37 ± 5.12 |
| pn (°) | 0.0536 | 0.2182 | 0.4751 | 1.0000 | 0.9775 | 0.8051 | 58.82 ± 11.37 | 58.20 ± 9.21 | 63.645 ± 11.54 |
| max TR (Nm) | 0.3462 | 0.0006 | 0.0032 | 0.0157 | 1.0000 | 0.0079 | 0.156 ± 0.037 | 0.200 ± 0.022 | 0.151 ± 0.034 |
| max Tωω (Nm) | 0.4445 | 0.0001 | 0.0004 | 0.0010 | 1.0000 | 0.0042 | 0.125 ± 0.038 | 0.179 ± 0.022 | 0.133 ± 0.021 |
| max Tp (Nm) | 0.5628 | <0.0001 | <0.0001 | 1.0000 | 0.0010 | 0.0010 | 0.100 ± 0.018 | 0.096 ± 0.007 | 0.064 ± 0.018 |
| max α (rad/s2) | 0.4445 | 0.0001 | 0.0004 | 0.0010 | 1.0000 | 0.0042 | 1602.9 ± 489.7 | 2301.0 ± 284.5 | 1704.1 ± 273.0 |
| max P (W) | 0.4352 | 0.0001 | 0.0004 | 0.0010 | 1.0000 | 0.0078 | 7.30 ± 3.14 | 12.33 ± 2.22 | 8.36 ± 2.35 |
| η (%) | 0.3468 | 0.0006 | 0.0032 | 0.0220 | 0.0061 | 1.0000 | 51.67 ± 5.04 | 60.57 ± 4.29 | 62.21 ± 9.53 |
| TR/ω (Nm/rps) | 0.4424 | 0.0001 | 0.0004 | 1.0000 | 0.0019 | 0.0018 | 0.0109 ± 0.0006 | 0.0109 ± 0.0004 | 0.0096 ± 0.0010 |
| Tω/ω (Nm/rps) | 0.3745 | 0.0003 | 0.0018 | 0.0115 | 1.0000 | 0.0042 | 0.0086 ± 0.0011 | 0.0098 ± 0.0005 | 0.0085 ± 0.0005 |
| Tp/ω (Nm/rps) | 0.8222 | <0.0001 | <0.0001 | 0.0010 | 0.0010 | 0.0010 | 0.0071 ± 0.0006 | 0.0053 ± 0.0004 | 0.0041 ± 0.0008 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fuss, F.K.; Doljin, B.; Ferdinands, R.E.D. Effect of the Grip Angle on Off-Spin Bowling Performance Parameters, Analysed with a Smart Cricket Ball. Proceedings 2018, 2, 204. https://doi.org/10.3390/proceedings2060204
Fuss FK, Doljin B, Ferdinands RED. Effect of the Grip Angle on Off-Spin Bowling Performance Parameters, Analysed with a Smart Cricket Ball. Proceedings. 2018; 2(6):204. https://doi.org/10.3390/proceedings2060204
Chicago/Turabian StyleFuss, Franz Konstantin, Batdelger Doljin, and René E. D. Ferdinands. 2018. "Effect of the Grip Angle on Off-Spin Bowling Performance Parameters, Analysed with a Smart Cricket Ball" Proceedings 2, no. 6: 204. https://doi.org/10.3390/proceedings2060204
APA StyleFuss, F. K., Doljin, B., & Ferdinands, R. E. D. (2018). Effect of the Grip Angle on Off-Spin Bowling Performance Parameters, Analysed with a Smart Cricket Ball. Proceedings, 2(6), 204. https://doi.org/10.3390/proceedings2060204





