Confinement Effect in a Thick Layer of LC Lanthanide Complex ^†

Abstract

The structure of metallomesogen complexes differs essentially from that of calamitic liquid crystals, which emerges in their physical properties. We studied anomalous features of the transition from the nematic to isotropic phase in the ytterbium-based liquid crystal complex. For this, two approaches were used. In the first approach, we showed that the experimental values of the dielectric and optical anisotropies measured near the phase transition turned out to be substantially smaller than their calculated values. This evidently occurs because the phase transition temperature in the deep region of the experimental cell differs from that near the surface of the cell. Secondly, the temperature of N–I transitions in metallomesogenic layers within glass sandwich cells is obtained directly by means of the polarization microscope method. It was found that the phase transition temperature drops in more than ten degrees when reducing the metallomesogenic layer thickness from 200 to 5 microns. The calamite liquid crystals show the confinement effect only within the interstice of the specific size smaller than one micron. An anomalous confinement effect can be caused by a strong interaction of the molecular complexes with each other.

1. Introduction

The recent years have witnessed considerable progress in the synthesis and studies of liquid-crystalline lanthanide complexes, owing to the progress in the physics of liquid crystals and in coordination and organic chemistry [1,2]. The molecular structure of complexes is considerably more sophisticated than that of classical liquid crystals. This feature, together with the presence of metal atoms in the complexes, account for their peculiar physical properties; in particular, most metallomesogens are smectics. A typical feature of metallomesogenic complexes is the combination of the optical and electrical anisotropies inherent in typical liquid crystals with the magnetic and electronic properties inherent in transition metal complexes. They exhibit efficient luminescence, and the magnetic susceptibility anisotropy of metallomesogens is orders of magnitude higher than that of organic liquid crystals [3,4]. The successful synthesis of nematic metallomesogens [5] opened up the possibility to obtain and study macroscopically ordered liquid-crystalline phases [6]. Systematic studies of metallomesogens revealed one more feature, which has not been deliberately investigated so far and is analyzed in this work. In particular, the first-order phase transition from the liquid-crystalline to isotropic phases can take place within a temperature range of one to several degrees. This should give rise to the coexistence of the anisotropic and isotropic phases and to effective anisotropy of physical properties being lower in this range than the anisotropy of the proper liquid-crystalline phase. In this work, we compared the electro-optical properties of the metallomesogen in the isotropic (I) phase with the optical and dielectric anisotropy of the metallomesogen determined in the nematic (N) phase. The anisotropy measured experimentally near the transition proved to be many times lower than the calculated value.

The cause for phase coexistence was determined by monitoring the phase transition by polarization microscopy. This is the effect of boundaries of the cell containing the sample at the N–I phase transition temperature, i.e., the confinement effect. In the case of classical liquid crystals placed into a thin cell or porous matrix, this effect is manifested if the cell (pore) characteristic dimension is less than a micrometer [7]. The confinement effect found in metallomesogens for layer thicknesses of an order of magnitude greater was a new and unexpected finding.

2. Methods

The liquid-crystalline complex studied in this work was tris[1-(4-(4-propylcyclohexyl) phenyl) octane-1,3-diono]-[5,5′-di(heptadecyl)-2,2′-bipyridineytterbium, designated as Yb(DDk_3-5)₃Bpy_17-17. It has both smectic A and nematic phases [5].

The electro-optical properties of an isotropic melt above the nematic–isotropic melt phase transition temperature were studied by considering the Kerr effect, which serves as a tool for examining phase transitions in mesogens [9,10]. The electric field-induced birefringence Δn_E is related to the Kerr constant K and the electric field strength E by the Kerr equation: Δn_E = KE². The electric birefringence in the isotropic melt was measured in rectangular pulse fields with strengths of up to 5 × 10³ V/cm. In order to eliminate the electrical conductivity and parasitic heating effects, short (0.5 ms) electric pulses with a repetition rate of less than 0.1 Hz were used. The Kerr cell with the sample was maintained at a constant temperature to within 0.1 °C.

For determining the conditions of existence of the two-phase liquid-crystal–isotropic melt system in the Yb(DDk_3-5)₃Bpy_17-17 mesogen, we examined the N–I transition in the planar and wedge-like layers of various thickness, d, by polarization microscopy. The samples were sandwiched between clean glasses whose surfaces were not treated in any way. The sample heating and cooling rates did not exceed 0.5 K/min.

3. Results and Discussion

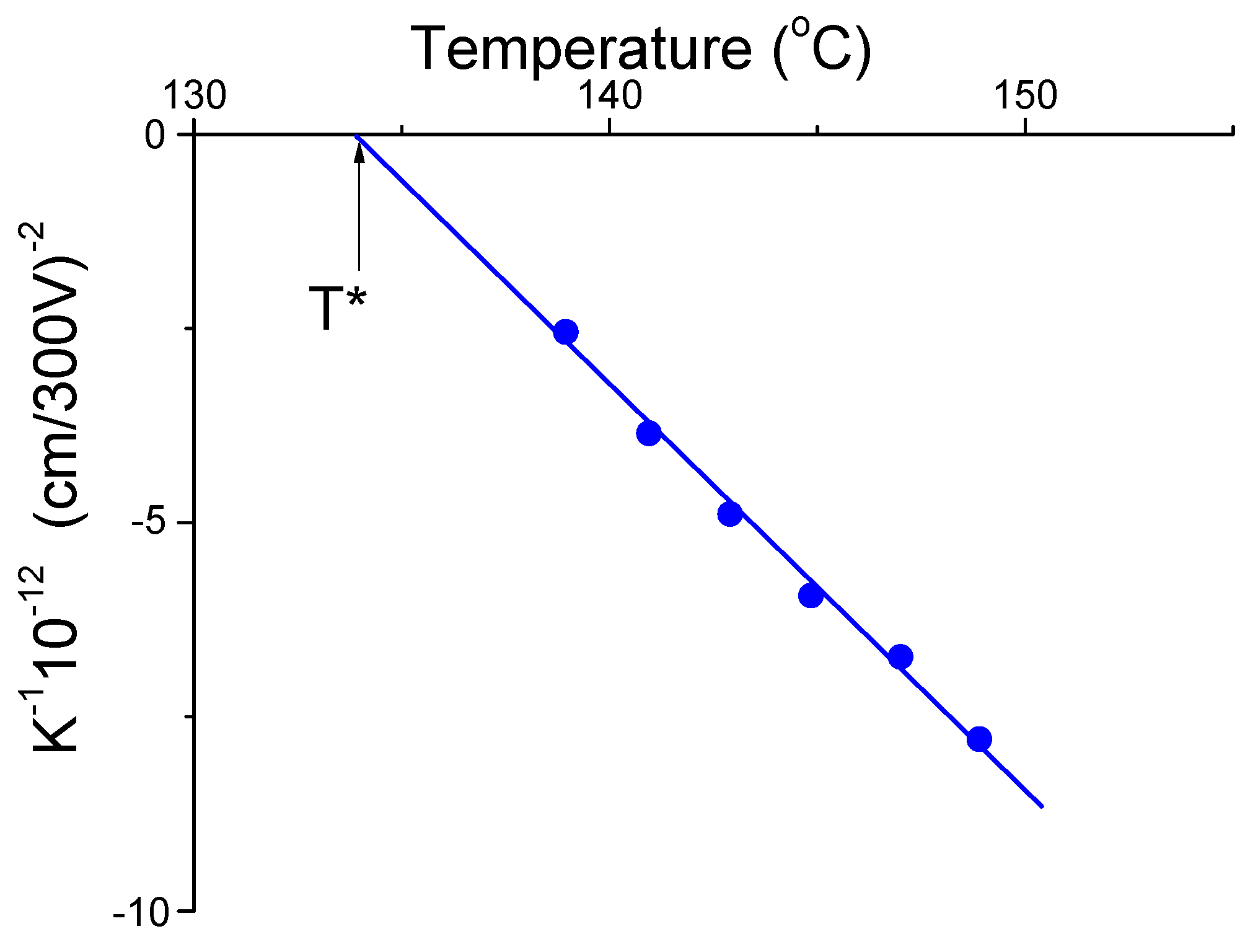
The plot for reciprocal of the Kerr constant 1/K versus temperature T is shown in Figure 1.

The EBR sign is negative, indicating that the permanent dipole moment of the complex forms an angle of more than 55° with its longitudinal axis. As the temperature is lowered, the absolute magnitude of the Kerr constant K increases and the reciprocal of the Kerr constant varies linearly; i.e., the dependence K ~ 1/(T − T*) holds. The electro-optical constant K(T − T*) is −2.0 × 10⁻⁸ (cm/300 V)⁻² K. By extrapolation of the temperature dependence of 1/K, the limiting temperature of existence of the isotropic phase was found to be T* = 133.9 °C.

A phenomenological approach to the description of the pretransition behavior of a liquid crystal was developed by De Gennes on the basis of the Landau phase transition theory [8]. In the I–N phase transition region, the free-energy density F in the presence of an electric field of strength E is expanded in the powers of the orientational order S, and consideration can be restricted to the quadratic term: $F(T)=F_0(T)+\frac{1}{2}a(T-T*)S^2-\frac{1}{12\pi }\Delta \epsilon E^2$ . Here, F₀(T) is the energy of the isotropic phase and Δε is the dielectric anisotropy. The coefficient a in the expansion is related to the heat of melting L in the following way: $L=a{T}_c{S}_c^2/2$ . The order parameter S_c corresponds to the order at the N–I phase transition temperature T_c. The Landau–De Gennes theory makes it possible to express the dielectric Δε_с and optical Δn_с anisotropies of a liquid crystal at temperature T_c in terms of the electro-optical constant of the isotropic phase K(T − T*) in the following way:

$$\Delta n_c\Delta {\epsilon }_c=24\pi LK(T-T*)/T_c$$

(1)

Equation (1) adequately describes the behavior of classical liquid crystals [11]. Using the measured electro-optical constant K(T − T*) and the values L = 8.0 × 10⁶ erg/cm³ and T_c = 127 °C, we calculated the anisotropy from equation (1) to be Δn_сΔε_с = −0.03. An absolutely different result is obtained upon multiplication of the experimentally determined optical [12] and dielectric [6] anisotropy values near the transition: Δn_сΔε_с = −0.00024. Evidently, the presence of the isotropic liquid phase in the anisotropic liquid near the phase transition decreases the value of Δn_сΔε_с by two orders of magnitude. This can be ascertained by using data on the mesophase anisotropy at low temperature, where an isotropic phase impurity is absent. Using the low-temperature values Δn = 0.08 and Δε = −1.9, we converted them to the temperature T_c, bearing in mind that the temperature dependence of Δn and Δε is a function of the order parameter: Δε ~ S and Δn ~ S. The usual values of the order parameter S are 0.7 in the low-temperature region and 0.4 in the close vicinity of T_c; from this, we find that the anisotropy decreases 1.75-fold near the transition, and then Δn_сΔε_с = −0.05. This result is already comparable with the value calculated from Equation (1). Thus, combined analysis of optical, dielectric, and electro-optical data indicates that the isotropic and anisotropic phases coexist in the vicinity of phase transition.

The specific behavior of metallomesogens in the N–I phase transition is manifested most clearly in the case of a cell of variable thickness; this is demonstrated by the micrograph in Figure 2.

As the isotropic melt is cooled, the formation of the liquid-crystalline phase starts at temperature T₁ from the region in which the layer thickness d = 200 μm. With decreasing temperature, the liquid crystal–isotropic phase boundary moves along the arrow towards part of the sample where d = 5 μm. Thus, the phase transition occurs in a ~10 °C temperature interval between T₁ and T₂, where T₁ is the higher temperature at which the mesophase is formed deep in the layer and T₂ is the minimal temperature at which the nematic phase is formed in the narrow part of the layer. The phase transition under the same conditions for a conventional calamitic occurs in an interval of less than 0.1 degrees; see Figure 3.

In 8- and 50-μm thick planar layers, the temperature interval T₁ − T₂ narrows down to reach a minimal value of about 1 °C in the thinnest layer, as one can see in the plot in Figure 4. The T₂ value is almost invariable as it characterizes the transition near the boundaries, whereas T₁ substantially depends on thickness. As follows from the plot, the curve should arrive at saturation near d = 1000 μm upon reaching the limiting temperature T* of the isotropic phase existence; for a nematic, T* differs from the temperature of the N–I transition in the bulk by less than one degree: T* ≈ T_c. In other words, the difference T* − T₂ = 14 °C corresponds to the greatest transition temperature shift for the metallomesogen Yb(DDk_3-5)₃Bpy_17-17 under the boundary conditions specified in the experiment.

The shift of the N–I transition temperature and, in some cases, also the transformation of the first-order phase transition into a continuous transition are caused by the influence of the extensive boundary on the order parameter in the melt [13]. It was found in experiments using thin layers of liquid-crystalline alkyl cyanobiphenyl with one free surface that the shift is determined by a combination of three factors: surface tension, boundary anchoring, and capillary condensation [7]. The shift increases as the characteristic size d decreases and the shift can be both positive and negative. A computer modeling of the N–I transition under confinement [14] demonstrated that there is no single universal scenario that would describe the transition properties as a function of d; the transition behavior being dependent only on intermolecular interaction details. This conclusion is consistent with our assumptions that the probable causes of the above-described phase behavior are related to the sophisticated molecular architecture of metallomesogenic complexes. The result of this study is practically significant, because it implies that the confinement effects can be both manifested under certain conditions and used in the existing electro-optical sensors, modulators, and other devices.