Abstract
Metallomesogenic lanthanide complexes can be used as a basis for developing magneto- and electro-optical devices. The magnitude and sign of the dielectric anisotropy both play a leading role in this case. However, any direct measurements of the dielectric anisotropy for the most part of the metallomesogenic complexes are highly problematic since they only have a smectic phase, and therefore there is no way to produce macroscopic homogeneous samples. This problem can be solved due to the similarity between the mechanism of the dielectric polarization in the liquid crystal phase and that of the electrical birefringence in the isotropic phase. Thereby, one can estimate the dielectric anisotropy in the liquid crystal phase by studying the electrical birefringence in the isotropic melt. We have studied complexes consisting of ions of rare-earth metals such as Dy, Er, Gd, Tb, and of alkylsulfate counterions and Schiff bases as being ligands. The number of methylene groups in aliphatic chains of counterions was varied between 0 and 12. It was found that in the series of the substances under investigation the magnitude as well as the sign of electro- optical effect in the isotropic phase depended on length of the counterions, but not depended on the metal ions used. Thus, dielectric anisotropy of smectic lanthanide complexes can be widely changed by variations of chemical structure of the counterions.
1. Introduction
Electric birefringence is used to study the isotropic melts of substances in a thermotropic liquid crystal state. Within the model of Landau-De Gennes phase transitions [1], it was shown that the properties of the isotropic phase such as the Kerr constant and the relaxation time of the Kerr effect are directly related to the optical and dielectric anisotropies and the rotational viscosity of the mesophase in the same substance [2,3,4,5]. Consequently, the electric birefringence method can also provide information on the characteristics of the liquid crystal phase. In this work, we use the electric birefringence method to study metallomesogenic lanthanide complexes [6,7], whose advantages include paramagnetic properties [8,9] and effective luminescence [10,11]. They are promising for application as liquid crystal materials in electro- and magneto-optical devices. The fundamentally important characteristic for this application is the anisotropy of physical properties, primarily dielectric and magnetic anisotropies, because they determine the possibility of controlling devices where liquid crystal materials are used as active elements. The anisotropy of the physical properties of liquid crystals and the relation of these properties to the molecular structure of these materials can be studied only in the presence of a nematic phase because the homogeneous macroscopic ordering of the optical axis (director) is easily created in a nematic and a liquid single crystal is formed. A macroscopically ordered smectic sample can also be obtained sometimes by cooling a uniformly ordered nematic. However, the synthesis of nematic lantha nide mesogens appeared to be very difficult: the first nematics had narrow intervals of existence in the mesophase and a high clearing temperature at which point they rapidly decomposed [12,13]. Thermostable nematic lanthanide-containing liquid crystals were obtained only recently [14,15]. The first studies of the optical [16] and dielectric [17] anisotropies in the nematic and smectic phases have been reported. However, the overwhelming majority of lanthanide complexes have only a smectic phase and form multidomain macroscopically disordered structures. For this reason, the direct study of the dielectric anisotropy of such metallomesogens and, therefore, the determination of its relation to the molecular structure are serious problems. We propose a possible solution to these problems based on the study and analysis of the electro-optical properties of an isotropic liquid phase of these materials.
2. Methods
In this work, we study a number of smectic-А complexes consisting of a lanthanide ion, alkyl sulfate counterions, and ligands with the general formula Ln(CnH2n+1SO4)2(CkH2k+1O-C6H3(OH)-CH=N-CmH2m+1)3. Their composition includes lanthanides Ln = Dy, Tb, Gd, and Er and various numbers k, m, and n of CH2 elements in aliphatic chains. In addition, we studied the Tb(NO3)2(CkH2k+1O-C6H3(OH)-CH=N-CmH2m+1)2, sample containing a nitrogen acid counterion without aliphatic elements. Electric birefringence in the isotropic phase was measured with a highly sensitive setup using the compensation method, involving a modulator of the elliptical polarization of light [4]. We used a pulsed electric field with the strength up to 2.5 × 103 V/cm, a rectangular pulse duration of 10 ms, and a pulse repetition frequency lower than 1 Hz in order to eliminate the negative effect of the electrical conductivity of the samples. Measurements were performed in a small Kerr cell for 15 mg of a material with an optical path length of 2 mm.
3. Results and Discussion
The Kerr constant K at various temperatures was calculated using the Kerr law ΔnE = КЕ2, where ΔnE is the field-induced birefringence. The Kerr constant K for all samples demonstrates a characteristic temperature dependence (Figure 1) according to which the inverse Kerr constant varies as 1/К ~ (T − T*), where T* is the temperature of the virtual second-order phase transition [1]. Using these data, we determined the temperature-independent electro-optical constant K(T − T*) and used it for the comparison of the electro-optical properties of complexes different in composition.
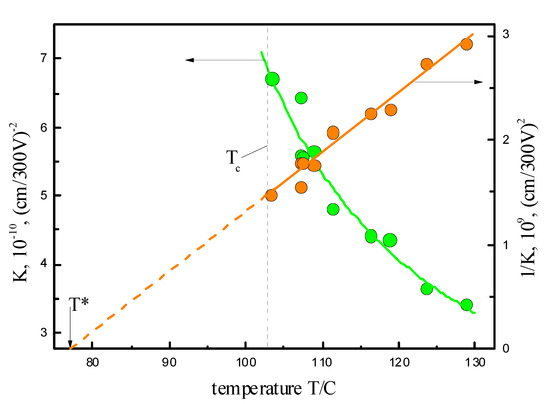
Figure 1.
Temperature dependences of the Kerr constant K and inverse quantity 1/K for the Tb(C2H5SO4)2(C12H25O–C6H3(OH)–CH=N–C17H35)3 complex. The temperature Tc of the smectic-А–isotropic phase transition and the temperature T* of a virtual second-order phase transition are indicated.
As is seen in Figure 2, K(T − T*) strongly depends on the number of aliphatic units n in alkyl sulfate counterions. At large n values, the sign of the Kerr effect is negative and the shortening of a counterion reduces the negative effect. Near n = 7, where the electrooptical effect nearly vanishes, the sign of the constant K changes to positive. These changes occur independently of the nature of the rare-earth metal and the length of the aliphatic ligand chains. The only metallomesogen with the shortest nitrogen-acid counterions, NO3, absent of methylene groups also has these properties. It is noteworthy that the number of CH2 units in counterions varied significantly by a factor of 12 (n = 0, 2, 8, or 12). Relative changes in the length of the aliphatic ligand chains are small (k = 12 or 14, m = 16, 17, or 18). Long aliphatic ligand chains are also involved in the formation of the spatial geometry of a complex and should affect the electro-optical properties. The variation of the length of ligands was very limited because of the choice of the optimal structure of ligands for the formation of a stable liquid crystal phase.
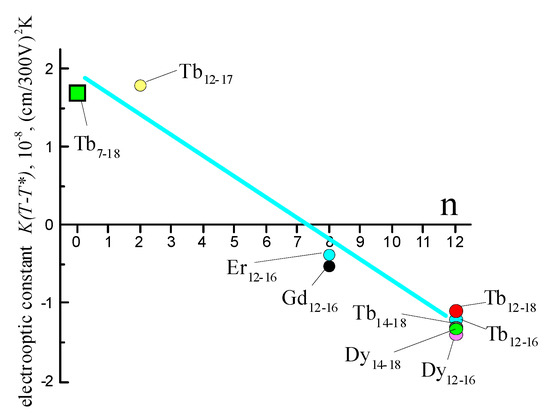
Figure 2.
Electro-optical constant versus the number n of methylene groups CH2 in the aliphatic chain of counterions. The composition of each complex is indicated near the points in the form Lnk−m, where Ln is the lanthanide ion and k and m are the numbers of methylene groups in ligands.
The resulting dependence (see Figure 2) can be interpreted as follows. Using the Landau–De Gennes theory, Chandrasekhar ([18], Chapter 2) proposed the following expression for the Kerr constant K in the isotropic phase of liquid crystals whose molecular structure has the axial symmetry of the optical and dielectric properties:
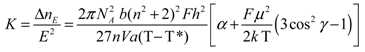
Here, NA is the Avogadro number; k is the Boltzmann constant; V is the molar volume; a is the coefficient in the expansion of the free energy of the melt in a series in the orientational order parameter S; n is the refractive index; b and α are the anisotropy parameters of the optical and electrical polarizabilities, respectively; F and h are the multipliers of the internal field; and μ and γ are the dipole moment and its angle, respectively. The magnitude and sign of K obviously depend crucially on the parameters μ and γ in square brackets in Equation (1) because the anisotropy parameter α is always positive for liquid crystal molecules. The electro-optical constants of the complexes are large, characteristic of polar liquid crystals [19,20]. This indicates the presence of a large dipole moment μ, and a change in the angle of inclination of this dipole moment to the longitudinal geometric axis of the complex leads to variations of the electro-optical constant at the variation of the composition. Equation (1) allows the computer simulation of the effect of the angle of inclination of a static dipole within a range of 0° to 90° on the dependence K(T) with the parameters of well-studied pentylcyanobiphenyl [21]. According to Equation (1) and Figure 3, when 0° < γ < 55°, the expression in square brackets is positive and K > 0. If 90° > γ > 55°, the expression in square brackets becomes negative and, correspondingly, K < 0.
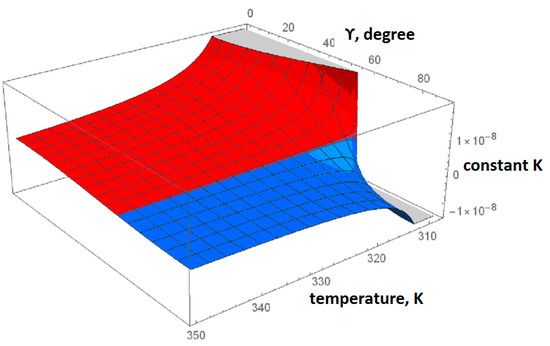
Figure 3.
Temperature dependence of the Kerr constant K at different angles of inclination γ of the static dipole moment to the longitudinal axis of the molecule as calculated by Equation (1) with the parameters of pentylcyanobiphenyl. Red indicates the area where K is positive, blue indicates where K is negative.
The dipole moment of the mesogenic complex is due to the system of coordination bonds inside a coordination sphere whose elements are a rare-earth ion, two alkyl sulfate counterions, and three ligands. The variation of the length of counterions leads to a change in the spatial geometry of the sphere and, thereby, the angle of the dipole moment. Even small deviations of the angle from the critical value γ ≈ 55 are enough to ensure the experimentally observed changes in the sign and magnitude of K.
For our purposes, it is important that the direction of the dipole moment similarly affects the dielectric anisotropy of the liquid crystal phase. The dielectric anisotropy parameter Δε is the difference between the relative permittivities along and across the director of the liquid crystal. The Maier–Meier theory [22], which describes the dielectric properties of a uniformly oriented liquid crystal, gives the following relation between the dielectric anisotropy and molecular parameters:
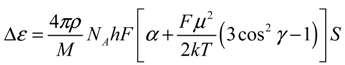
The expressions in square brackets in Equations (1) and (2) are identical because the same orientational mechanism is present both in the dielectric polarization of the mesophase and in the electro-optical effect in the isotropic melt. Previous experimental works [4,23] confirm this conclusion. The comparative analysis of the mechanisms of dipole orientation depending on the temperature and frequency of the electric field was performed by the dielectric spectroscopy and electric birefringence methods in a sinusoidal field for Н-44 and Н-21 calamitic nematics, whose molecules have different angles of inclination γ of dipoles. It was shown that Δε and K at low frequencies are positive for Н-44 (γ = 47°) and negative for Н-21 (γ = 59°).
To summarize, it has been shown that mesogenic lanthanide complexes with Schiff bases and with the necessary signs and magnitudes of the electro-optical effect, as well as the signs and magnitudes of the dielectric anisotropy of the liquid crystal phase, can be obtained by varying the length of the counterions.
Author Contributions
S.P. conceived and designed the experiments; G.P., V.R. and I.L. performed the experiments and analyzed the data; A.Z. performed computer modeling, S.P. wrote the paper.
Acknowledgments
The authors are grateful to Yu. Galyametdinov for providing the samples, and are grateful to E. Rjumtsev for assistance in the work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- De Gennes, P.G. Short range order effects in the isotropic phase of nematics and cholesterics. Mol. Cryst. Liq. Cryst. 1971, 12, 193–214. [Google Scholar] [CrossRef]
- Coles, H.J. Laser and electric field induced birefringence studies on the cyanobiphenyl homologues. Mol. Cryst. Liq. Cryst. 1978, 49, 67–74. [Google Scholar] [CrossRef]
- Yamamoto, R.; Ishihara, S.; Hayakawa, S.; Morimoto, K. The Kerr constants and relaxation times in the isotropic phase of nematic homologous series. Phys. Lett. 1978, 69A, 276–278. [Google Scholar] [CrossRef]
- Tsvetkov, N.V.; Rjumtsev, E.I. Kerr-effect in the isotropic liquid phase of nematogens. Mol. Cryst. Liq. Cryst. 1986, 133, 125–134. [Google Scholar] [CrossRef]
- Ryumtsev, E.I.; Polushin, S.G.; Tarasenko, K.N.; Kovshik, A.P. Equilibrium and dynamic electrooptical properties of nematic and isotropic phases of 4-n-alkoxy-4′-cyanobiphenyls. Zhurnal Fizicheskoi Khimii 1995, 69, 940–943. [Google Scholar]
- Serrano, J.L. Metallomesogenes, Synthesis, Properties and Applications; VCH: New York, NY, USA, 1996. [Google Scholar] [CrossRef]
- Binnemans, K.; Gorller-Walrand, C. Lanthanide-containing liquid crystals and surfactants. Chem. Rev. 2002, 102, 2303–2345. [Google Scholar] [CrossRef]
- Galyametdinov, Y.G.; Haase, W.; Malykhina, L.; Prosvirin, A.; Bikchantaev, I.; Rakmatullin, A.; Binnemans, K. Synthesis, mesomorphism, and unusual magnetic behaviour of lanthanide complexes with perfluorinated counterions. J. Chem. Eur. 2001, 7, 99–105. [Google Scholar] [CrossRef]
- Galyametdinov, Y.G.; Haase, W.; Goderis, B.; Moors, D.; Driesen, K.; Van Deun, R.; Binnemans, K. Magnetic alignment study of rare-earth-containing liquid crystals. J. Phys. Chem. B 2007, 111, 13881–13885. [Google Scholar] [CrossRef][Green Version]
- Bünzly, J.C.; Piguet, C. Taking advantage of luminescent lanthanide ions. Chem. Soc. Rev. 2005, 34, 1048–1077. [Google Scholar] [CrossRef]
- Eliseeva, S.V.; Bünzli, J.C. Lanthanide luminescence for functional materials and bio-sciences. Chem. Soc. Rev. 2010, 39, 189–227. [Google Scholar] [CrossRef]
- Van Deun, R.А.; Parac-Vogt, T.N.; Van Hecke, K.; Van Meervelt, L.; Binnemans, K.; Guillon, D.; Donnio, B. Liquid-crystalline azines formed by the rare-earth promoted decomposition of hydrazide «habbe» ligands: Structural and thermal properties. J. Mater. Chem. 2003, 13, 1639–1645. [Google Scholar] [CrossRef]
- Cardinaels, T.; Driesen, K.; Parac-Vogt, T.N.; Heinrich, B.; Bourgogne, C.; Guillon, D.; Donnio, B.; Binnemans, K. Design of high coordination number metallomesogens by decoupling of the complex-forming and mesogenic groups: Nematic and lamello-columnar mesophases. Chem. Mater. 2005, 17, 6589–6598. [Google Scholar] [CrossRef]
- Galyametdinov, Y.G.; Knyazev, A.A.; Dzhabarov, V.I.; Cardinaels, T.; Driesen, K.; Gorller-Walrand, C.; Binnemans, K. Polarized luminescence from aligned samples of nematogenic lanthanide complexes. Adv. Mater. 2008, 20, 252257. [Google Scholar] [CrossRef]
- Dzhabarov, V.I.; Knyazev, A.A.; Strelkov, M.V.; Molostova, E.Y.; Schustov, V.A.; Haase, W.; Galyametdinov, Y.G. Tris(β-diketonates) lanthanum nematic adducts. Liq. Cryst. 2010, 37, 285–291. [Google Scholar] [CrossRef]
- Kovshik, A.P.; Krainyukov, E.S.; Kovshik, S.A.; Knyazev, A.A.; Galyametdinov, Y.G.; Ryumtsev, E.I. Optical anisotropy of liquid_crystal lanthanide complexes. Opt. Spectrosc. 2014, 116, 56–61. [Google Scholar] [CrossRef]
- Dobrun, L.A.; Sakhatskii, A.S.; Kovshik, A.P.; Ryumtsev, E.I.; Knyazev, A.A.; Galyametdinov, Y.G. Dielectric properties of an ytterbium_based nematic liquid_crystal complex. JETP Lett. 2014, 99, 133–135. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Liquid Crystal; Cambridge University Press: Cambridge, UK, 1977. [Google Scholar]
- Polushin, S.G.; Rogozhin, V.B.; Ryumtsev, E.I.; Galyametdinov, Y.G. Electrooptical properties of mesogenic rare earth complexes in isotropic melts. Dokl. Phys. Chem. 2014, 455, 64–66. [Google Scholar] [CrossRef]
- Polushin, S.G.; Rogozhin, V.B.; Ryumtsev, E.I.; Lezov, A.V. The Kerr effect in the vicinity of the transition from the isotropic to smectic-A phase. Russ. J. Phys. Chem. A 2006, 80, 1016–1020. [Google Scholar] [CrossRef]
- Dunmur, D.A.; Tomes, A.E. The Pretransitional Kerr effect in 4-n-pentyl-4′-cyanobiphyenyl. Mol. Cryst. Liq. Cryst. 1981, 76, 231–240. [Google Scholar] [CrossRef]
- Maier, W.; Meier, G. Eine einfache theorie der dielektrischen eigenschaften homogen orientierter kristallinglussiger phasen des nematischen typs. Z. Naturforsch. 1961, 16A, 262–267. [Google Scholar] [CrossRef]
- Ryumtsev, E.I.; Rotinyan, T.A.; Kovshik, A.P.; Tsvetkov, V.N. Dispersion of electric birefringence in isotropic phase of nematic liquid crystals. Sov. Phys. Crystallogr. 1982, 27, 1143–1147. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).