Multiscale Simulation of Surface Defect Influence in Nanoindentation by the Quasi-Continuum Method †
Abstract
:1. Introduction
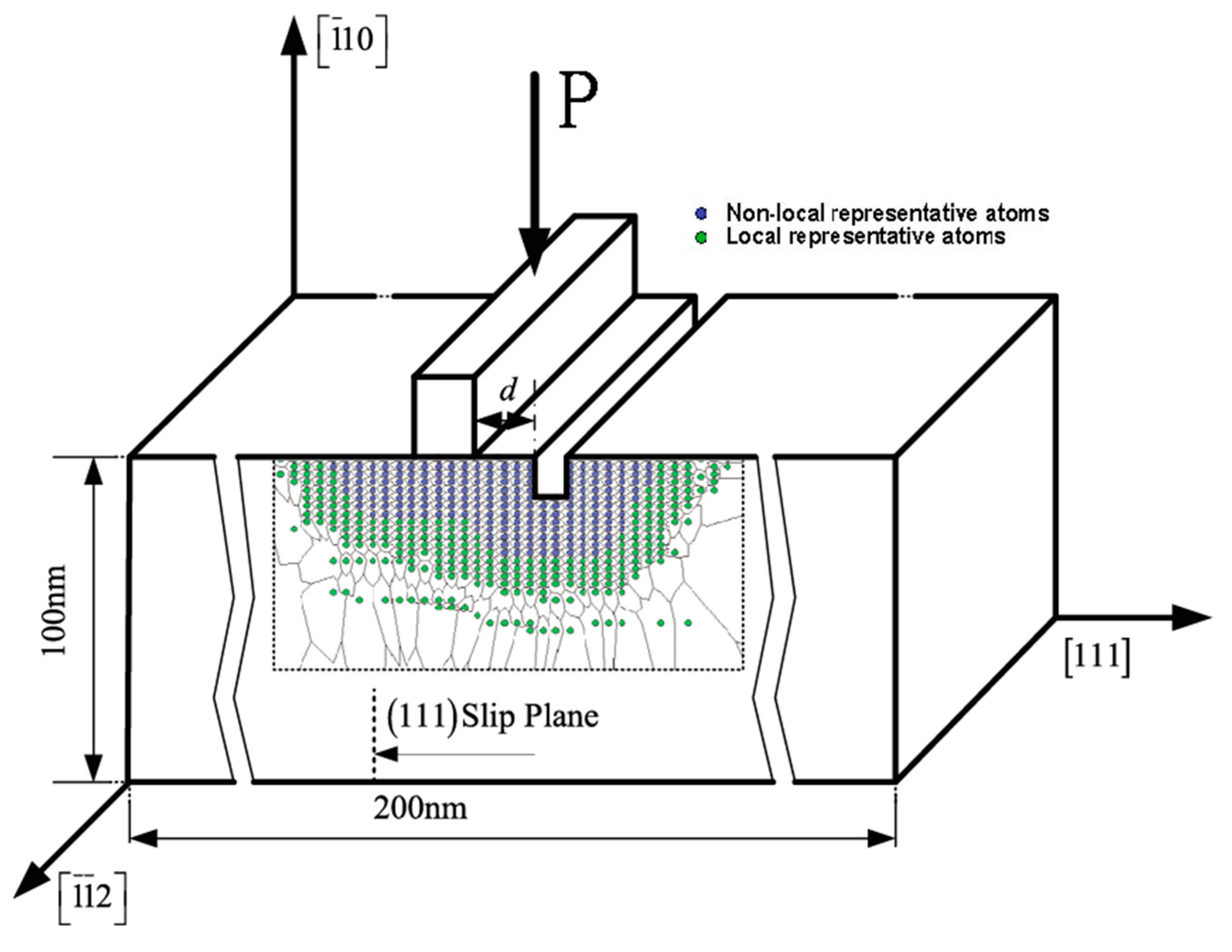
2. Methodology
3. Results and Discussion
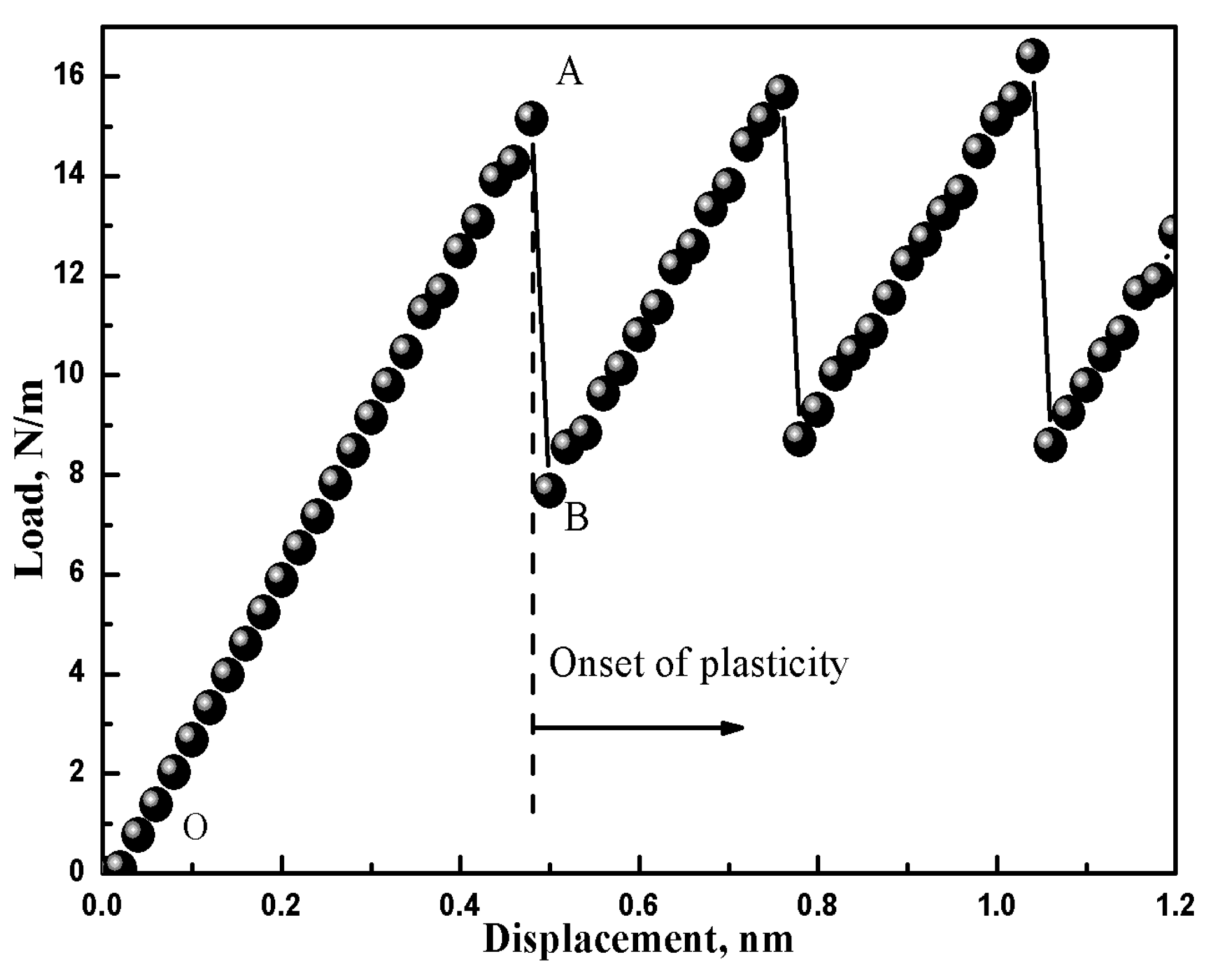
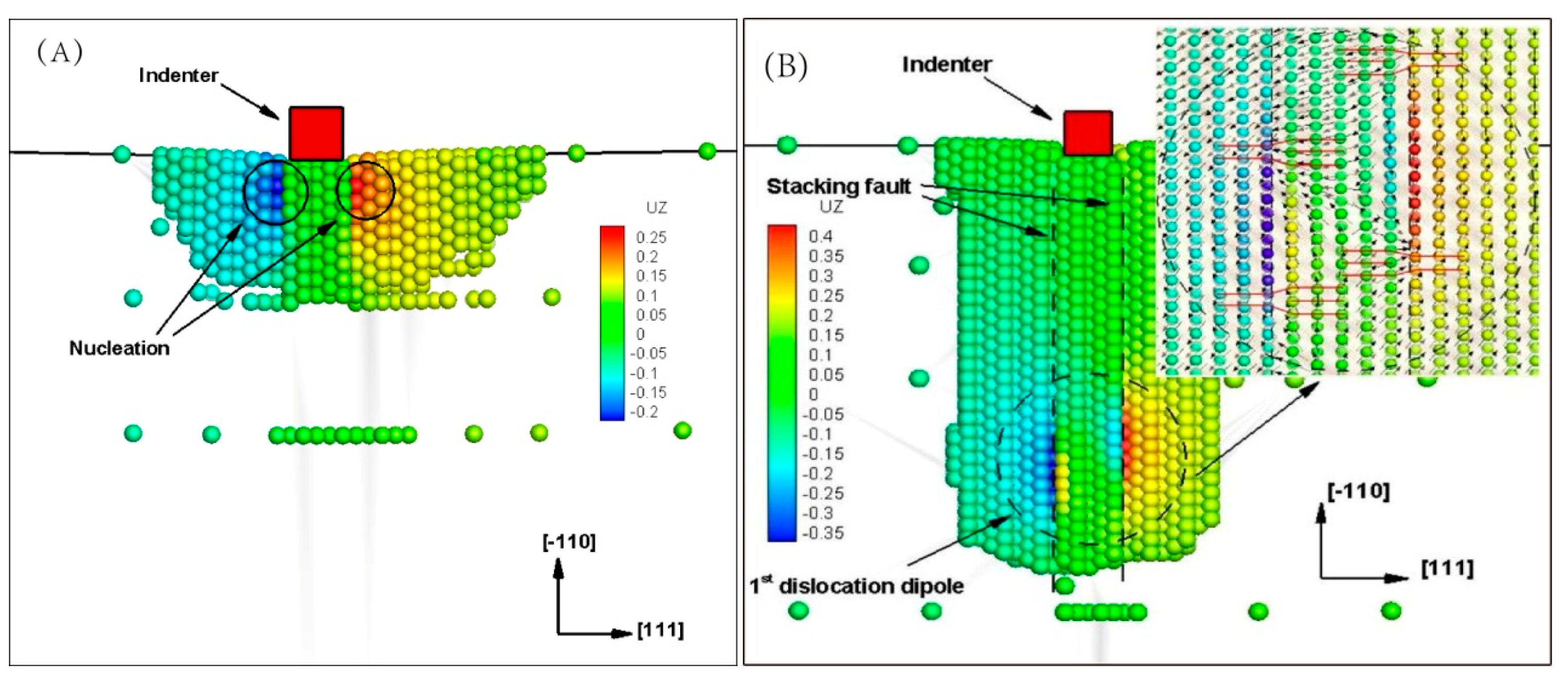
3.1. Nanohardness in the Case of No Surface Defect
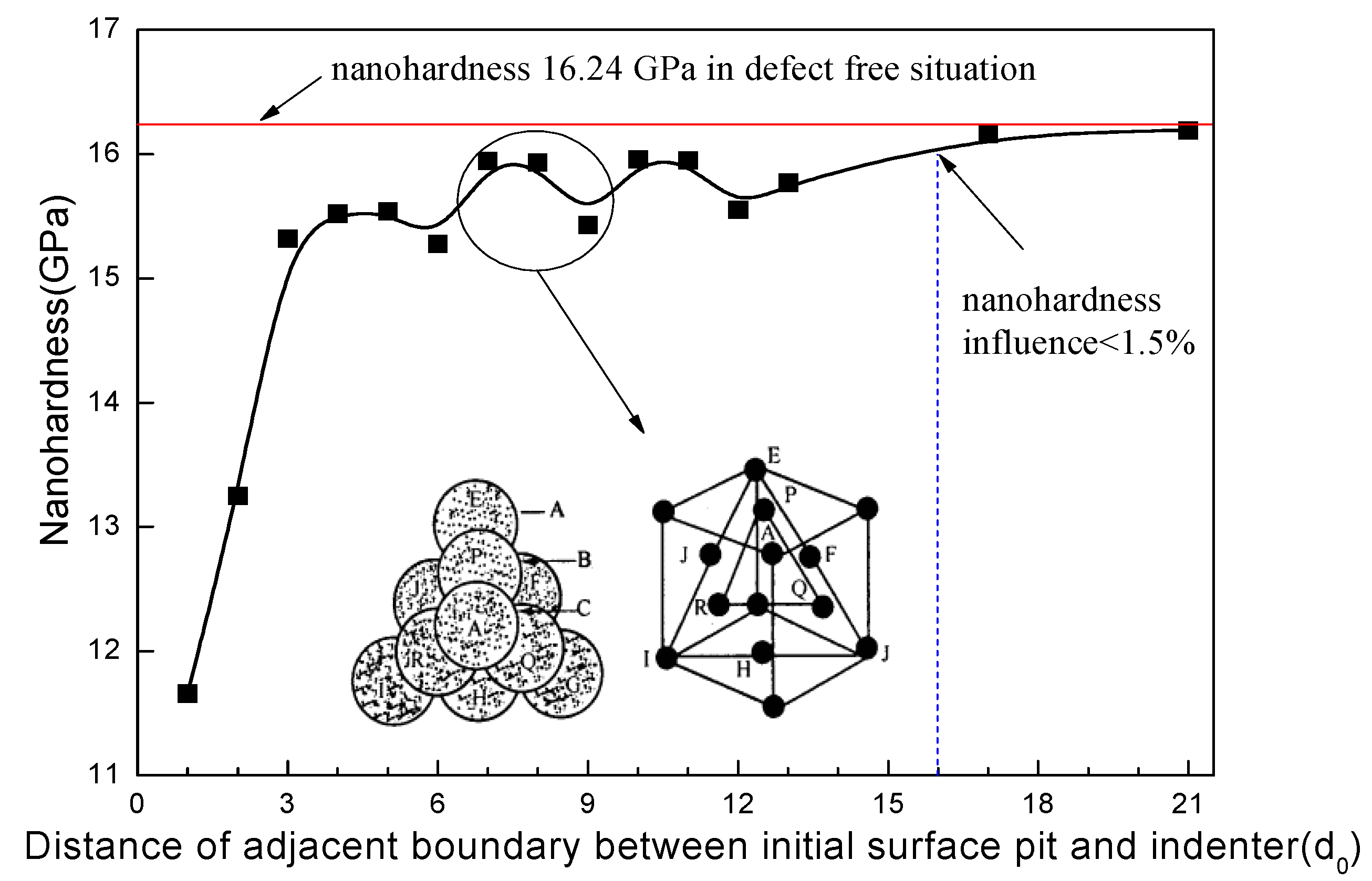
3.2. Nanohardness with Various Distances between Surface Defect and Indenter
3.3. Formula Modification of Necessary Load for Elastic-to-Plastic Transition
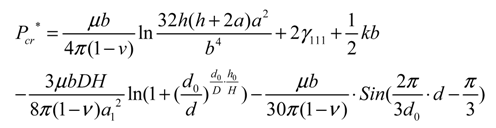
4. Conclusions
- The pitted surface plays a great role in the emission of dislocation that causes a significant reduction in nanohardness, compared with the defect-free situation.
- As the distance between the pit and indenter increases, the nanohardness increases in a wave pattern associated with a cycle of three atoms, which is closely related to periodic atoms arrangement on {111} atomic close-packed planes of face-centered cubic metal; when the adjacent distance between the pit and indenter is more than 16 atomic spacing, there is almost no effect on nanohardness, suggesting that each material has such a critical value.
- The theoretical formula for the necessary load of the elastic-plastic transition of Al film has been reasonably and efficiently modified with an initial surface pit. This modified formula has performed well with regards to the decreasing trend of nanohardness as the distance between the pit and indenter increases, and such a trend greatly agrees with the experimental results of the surface step with various distances. Such modification may contribute to the investigation of material properties with surface defects, particularly in nanoindentation and microchips.
Acknowledgments
References
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Li, X.D.; Bhushan, B. A review of nanoindentation continuous stiffness measurement technique and its applications. Mater. Charact. 2002, 48, 11–36. [Google Scholar] [CrossRef]
- Bamber, M.J.; Cooke, K.E.; Mann, A.B.; Derby, B. Accurate determination of Young’s modulus and Poisson’s ratio of thin films by a combination of acoustic microscopy and nanoindentation. Thin Solid Films 2001, 399, 299–305. [Google Scholar] [CrossRef]
- Zhu, P.Z.; Hu, Y.Z.; Fang, F.Z.; Wang, H. Multiscale simulations of nanoindentation and nanoscratch of single crystal copper. Appl. Surf. Sci. 2012, 258, 4624–4631. [Google Scholar] [CrossRef]
- Chen, J.; Bull, S.J. Assessment of the toughness of thin coatings using nanoindentation under displacement control. Thin Solid Films 2006, 494, 1–7. [Google Scholar] [CrossRef]
- Sangwal, K.; Gorostiza, P.; Sanz, F. Atomic force microscopy study of nanoindentation creep on the (100) face of MgO single crystals. Surf. Sci. 2000, 446, 314–322. [Google Scholar] [CrossRef]
- Zhang, T.H.; Yang, Y.M. The application of nanohardness technology in the mechanical properties testing of surface engineering. Chin. Mech. Eng. 2002, 24, 85–88. [Google Scholar]
- Mitchell, T.E. Dislocations and plasticity in single crystals of face centered cubic metals and alloys. Prog. Appl. Mater. Res. 1964, 6, 117–238. [Google Scholar]
- Mitchell, J.W. Growth and Perfection of Crystals; Doremus, R.H., Roberts, B.W., Turnbull, D., Eds.; Wiley: New York, NY, USA, 1958; pp. 386–389. [Google Scholar]
- Yang, B.; Vehoff, H. Dependence of nanohardness upon indentation size and grain size—A local examination of the interaction between dislocations and grain boundaries. Acta Mater. 2007, 55, 849–856. [Google Scholar] [CrossRef]
- Soifer, Y.M.; Verdyan, A.; Kazakevich, M.; Rabkin, E. Nanohardness of copper in the vicinity of grain boundaries. Scr. Mater. 2002, 47, 799–804. [Google Scholar] [CrossRef]
- Yu, W.S.; Shen, S.P. Multiscale analysis of the effects of nanocavity on nanoindentation. Comp. Mat. Sci. 2009, 46, 425–430. [Google Scholar] [CrossRef]
- Shan, D.; Yuan, L.; Guo, B. Multiscale simulation of surface step effects on nanoindentation. Mat. Sci. Eng. A 2005, 412, 264–270. [Google Scholar] [CrossRef]
- Keily, J.D.; Hwang, R.Q.; Houston, J.E. Effect of surface steps on the plastic threshold in nanoindentation. Phys. Rev. Lett. 1998, 81, 4424–4427. [Google Scholar] [CrossRef]
- Li, J.W.; Ni, Y.S.; Lin, Y.H.; Luo, C. Multiscale simulation of nanoindentation on Al thin film. Acta Metall. Sin. 2009, 45, 129–136. [Google Scholar]
- Zhang, Z.L.; Ni, Y.S. Multiscale analysis of delay effect of dislocation nucleation with surface pit defect in nanoindentation. Comp. Mat. Sci. 2012, 62, 203–209. [Google Scholar] [CrossRef]
- Qin, Z.D.; Wang, H.T.; Ni, Y.S. Multiscale simulations of FCC Al nanoindentation. Chin. Q. Mech. 2007, 1, 46–53. [Google Scholar]
- Tadmor, E.B. The Quasicontinuum Method. PhD Thesis, Brown University, Providence, RI, USA, 1996. [Google Scholar]
- Ercolessi, F.; Adams, J.B. Interatomic potentials from first-principles calculations: The force-matching method. Europhys. Lett. 1994, 26, 583–588. [Google Scholar] [CrossRef]
- Tadmor, E.B.; Ortiz, M.; Phillips, R. Quasicontinuum analysis of defects in solids. Philos. Mag. A 1996, 73, 1529–1563. [Google Scholar] [CrossRef]
- Tadmor, E.B.; Phillips, R.; Ortiz, M. Mixed atomistic and continuum models of deformation in solids. Langmuir 1996, 12, 4529–4534. [Google Scholar] [CrossRef]
- Shenoy, V.B.; Miller, R.; Tadmor, E.B.; Rodney, D.; Phillips, R.; Ortiz, M. An adaptive finite element approach to atomic-scale mechanics—The quasicontinuum method. Mech. Phys. Solids. 1999, 47, 611–642. [Google Scholar] [CrossRef]
- Nanoindentation. Available online: https://en.wikipedia.org/wiki/Nanoindentation (accessed on 2 May 2018).
- Tadmor, E.B.; Miller, R.; Phillips, R. Nanoindentation and incipient plasticity. J. Mater. Res. 1999, 14, 2233–2250. [Google Scholar] [CrossRef]
- Jiang, W.G.; Li, J.W.; Su, J.J.; Tang, J.L. Quasicontinuum analysisi of indenter size effect in nanoindentation tests. Chin. J. Solid Mech. 2007, 4, 375–379. [Google Scholar]
- Crystal Strucrure. Available online: https://en.wikipedia.org/wiki/Crystal_structure (accessed on 20 June 2018).
- Abu Al-Rub, R.K.; Voyiadjis, G.Z. A physically based gradient plasticity theory. Int. J. Plast. 2006, 22, 654–684. [Google Scholar] [CrossRef]


| Distance (d0) | QC Data (N/m) | Theory Load (N/m) | Data Difference (N/m) |
|---|---|---|---|
| 3 | 14.28 | 18.02 | 3.75 |
| 4 | 14.46 | 17.29 | 2.83 |
| 5 | 14.48 | 17.88 | 3.39 |
| 6 | 14.24 | 17.41 | 3.15 |
| 7 | 14.86 | 17.96 | 3.14 |
| 8 | 14.85 | 17.65 | 2.83 |
| 9 | 14.38 | 17.92 | 3.07 |
| 10 | 14.87 | 17.87 | 3.49 |
| 11 | 14.86 | 18.03 | 3.16 |
| 12 | 14.49 | 17.56 | 2.70 |
| 13 | 14.70 | 17.99 | 3.50 |
| 17 | 15.06 | 18.04 | 3.34 |
| 21 | 15.09 | 18.17 | 3.11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Zhang, J.; Ni, Y.; Wang, C.; Jiang, K.; Ren, X. Multiscale Simulation of Surface Defect Influence in Nanoindentation by the Quasi-Continuum Method. Proceedings 2018, 2, 1113. https://doi.org/10.3390/IECC_2018-05246
Zhang Z, Zhang J, Ni Y, Wang C, Jiang K, Ren X. Multiscale Simulation of Surface Defect Influence in Nanoindentation by the Quasi-Continuum Method. Proceedings. 2018; 2(14):1113. https://doi.org/10.3390/IECC_2018-05246
Chicago/Turabian StyleZhang, Zhongli, Jinming Zhang, Yushan Ni, Can Wang, Kun Jiang, and Xuedi Ren. 2018. "Multiscale Simulation of Surface Defect Influence in Nanoindentation by the Quasi-Continuum Method" Proceedings 2, no. 14: 1113. https://doi.org/10.3390/IECC_2018-05246
APA StyleZhang, Z., Zhang, J., Ni, Y., Wang, C., Jiang, K., & Ren, X. (2018). Multiscale Simulation of Surface Defect Influence in Nanoindentation by the Quasi-Continuum Method. Proceedings, 2(14), 1113. https://doi.org/10.3390/IECC_2018-05246




