Abstract
Co-resonantly coupled cantilever sensors have recently been introduced as a very promising concept to strongly increase the sensitivity of dynamic-mode cantilever MEMS sensors (several orders of magnitude experimentally demonstrated) while maintaining the ease of detection. Mechanical coupling and eigenfrequency matching of a micro- and a nanocantilever lead to a coupled system where any interaction at the highly sensitive nanocantilever alters the oscillatory state of the entire system which is detected at the microcantilever with standard laser-based methods. The coupled system’s sensor properties are described by effective parameters which depend on the subsystems’ properties and the degree of eigenfrequency matching. Here, the focus is on the implications of the effective properties on sensor performance with regard to sensitivity and detectability, which will be illustrated by an exemplary sensor model.
1. Introduction
Co-resonant cantilever sensors have been shown to tremendously increase the signal strength in proof-of-principle experiments in cantilever magnetometry and magnetic force microscopy (MFM) [1,2,3]. Since the measurement principle is only based on the coupling and eigenfrequency matching (termed as co-resonance) of a micro- and a nanocantilever, it could potentially by extended to other applications for dynamic-mode cantilever sensors, for example gas sensing (’artificial nose’) [4] or mass sensors [5].
The co-resonant coupling allows to access the high sensitivity of a nanocantilever with regard to external influences like force gradients or mass changes, while the oscillation detection is realized with conventional laser-based methods at the microcantilever. Since two oscillating beams are coupled, the amplitude response curve of the system features two resonance peaks whose amplitude and resonance frequency can be tracked as measurement signal [6].
For a single cantilever, the features of a resonance peak, e.g., the quality factor Q and the frequency shift ∆f in response to an external interaction, are determined by the cantilever properties which include the beam’s spring constant k, effective mass m and damping behavior described by the damping constant d. Consequently, for the coupled system, the features of the two resonance peaks are defined by a mixture of both beams’ properties and depend on the degree of eigenfrequency matching. Hence, each resonance peak can be described by a set of effective properties which in turn determine sensitivity and detectability [7].
From a sensor design point of view, the ability to predict and therefore tailor sensor performance for a desired application is crucial. Consequently, it is necessary to study the interplay between cantilever properties and frequency matching of the co-resonantly coupled system in detail and derive simplified analytical expressions to describe the effective sensor properties.
2. Modelling of a Co-Resonantly Coupled Sensor
For each of its eigenfrequencies, a mechanical oscillation-based sensor can be described by a harmonic oscillator model with lumped elements [8]. Likewise, the co-resonantly coupled system can be represented by a coupled harmonic oscillator with the individual beams’ spring constant k1,2, effective mass m1,2 and quality factor Q1,2, for each of its eigenfrequency matching combinations. Please note that the damping element di and quality factor Qi are related by Qi = /di; i = 1, 2. The model shown in Figure 1a has been used for the derivation of the expressions for effective sensor properties.
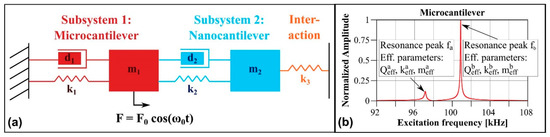
Figure 1.
(a) Coupled harmonic oscillator model for a co-resonantly coupled cantilever system. Each subsystem 1, 2 is represented by a spring k1,2, a damping element d1,2 and effective mass m1,2. The driving force is applied to subsystem 1 and an external interaction applied at the nanocantilever can be modelled by an additional spring k3 which represents a force gradient. (b) Amplitude response curve of the coupled system calculated for the microcantilever (amplitude normalized to the greatest value within the curve) and the parameters given in Table 1 for −2% eigenfrequency deviation, i.e., f2 = 98 kHz. The relevant definitions are indicated.
In order to give some graphical representation of the effective sensor properties, an exemplary sensor with parameters summarized in Table 1 is considered. These numerical values are based on experimental sensor realizations [1,2].

Table 1.
Exemplary sensor parameters based on experimental sensors for the individual micro- (1) and nanocantilever (2) before eigenfrequency matching (upper part). The lower part of the table summarizes the effective properties for both resonance peaks a and b for −2% eigenfrequency matching of micro- and nanocantilever.
Figure 1b depicts an exemplary amplitude response curve of the coupled system obtained for the microcantilever and based on the parameters from Table 1 and for −2% eigenfrequency deviation, i.e., the nanocantilever’s eigenfrequency is 2% lower than that of the microcantilever. Two resonance peaks are clearly visible and to distinguish between the effective properties of these resonance peaks and the properties of the individual beams, the subscript a, b will be used for the former and 1, 2 for the latter. Thereby, a always denotes the left resonance peak at the lower frequency and b the right one (higher frequency) of the coupled system as indicated in Figure 1b.
3. Effective Sensor Properties
The effective sensor properties depend on the degree of eigenfrequency matching and the parameters of the individual beams. The main parameters which determine sensor performance are the effective spring constant (for force sensors)/effective mass (for mass sensors) and effective quality factor, which affect sensitivity and detectability, respectively [9].
Since the complete derivation of all effective properties is outlined in detail in [7], the focus here will be on the practically relevant conclusions for sensor applications. Therefore, the exemplary sensor characteristics summarized in Table 1 will be used.
As it is evident from the amplitude response curve of the microcantilever in Figure 1b, two resonance peaks with different shape and height can be identified, leading to the assumption that each one is described by its own set of effective properties [10].
Graphs for the effective spring constant and quality factor are depicted in Figure 2 for the exemplary sensor parameters from Table 1. In that case, the eigenfrequency ω1 was kept constant while the eigenfrequency of the nanocantilever ω2 was varied, hence ∆ωeigen = (ω2 − ω1)/ω1.
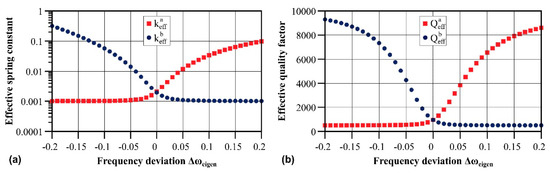
Figure 2.
(a) Effective spring constant and (b) effective quality factor for left (index a, lower frequency) and right (index b, higher frequency) resonance peak of the co-resonantly coupled system with exemplary parameters from Table 1. Please note that the y-axis in (a) has logarithmic spacing for better visibility.
Assuming that the resonance peak with the higher amplitude is experimentally measured (corresponding to the upper branches in Figure 2), the minimal achievable effective spring constant is 2k2. Hence, the nanocantilever’s stiffness mainly defines the sensitivity for each resonance peak of the coupled system, which is described by the frequency shift in response to an external interaction k3:
While Equation (1) relates to a force gradient interaction on the sensor, a similar relation is found for a changeable mass load [11]. In that case, k3 is substituted by the additional mass ∆m and by which is an effective mass for each resonance peak obtained by .
A similar result as for the effective spring constant is found for the effective quality factor (Figure 2b), which is always reduced in comparison to the highest quality factor of the system. However, if the resonance peak with the higher amplitude is considered in a measurement, the effective quality factor will never be smaller than approximately twice the smallest individual quality factor in the system. Hence, while a decrease in cantilever size usually reduces the quality factor, the co-resonant coupling partly counteracts this effect and leads to a better detectability for the coupled system compared to an individual nanocantilever. These consideration show that, depending on the application, a balance has to be found between the increase of sensitivity (lower effective spring constant/effective mass) and the detectability and signal-to-noise-ratio (effective quality factor).
4. Conclusions
Effective sensor properties are crucial for understanding and predicting the sensor performance for a novel co-resonantly coupled dynamic-mode cantilever sensor with regard to sensitivity and detectability. In the framework of the presented investigation, simplified analytical descriptions for the effective sensor properties have been derived, showing their dependence on the degree of eigenfrequency matching and on the individual subsystem’s properties. Here, the focus was on illustrating the effective properties’ implications on sensor performance based on exemplary sensor characteristics to stress the importance of understanding these key parameters. Based on this groundwork, sensor performance can now be estimated and tailored for specific applications in a fast and easy manner, thereby paving the way for many prospective implementations of the co-resonant sensor concept.
Funding
This research was funded by Deutsche Forschungsgemeinschaft DFG grant number KO 5508/1-1.
Acknowledgments
The author would like to thank Christopher F. Reiche for inspiring discussions.
Conflicts of Interest
The author declares no conflict of interest.
References
- Körner, J.; Reiche, C.F.; Büchner, B.; Gerlach, G.; Mühl, T. Signal enhancement in cantilever magnetometry based on a co-resonantly coupled sensor. Beilstein J. Nanotechnol. 2016, 7, 1033. [Google Scholar] [CrossRef] [PubMed]
- Körner, J.; Reiche, C.F.; Ghunaim, R.; Fuge, R.; Hampel, S.; Büchner, B.; Mühl, T. Magnetic properties of individual Co2FeGa Heusler nanoparticles studied at room temperature by a highly sensitive co-resonant cantilever sensor. Sci. Rep. 2017, 7, 8881. [Google Scholar] [CrossRef] [PubMed]
- Reiche, C.F.; Körner, J.; Büchner, B.; Mühl, T. Bidirectional scanning force microscopy probes with co-resonant sensitivity enhancement. In Proceedings of the IEEE 15th International Conference on Nanotechnology, Rome, Italy, 27–30 July 2015; p. 1222. [Google Scholar] [CrossRef]
- Baller, M.K.; Lang, H.P.; Fritz, J.; Gerber, C.; Gimzewski, J.K.; Drechsler, U.; Rothuizen, H.; Despont, M.; Vettiger, P.; Battiston, F.M.; Ramseyer, J.P.; Fornardo, P.; Meyer, E.; Güntherodt, H.J. A cantilever array-based artificial nose. Ultramicroscopy 2000, 82, 1. [Google Scholar] [CrossRef]
- Martínez-Martín, D.; Fläschner, G.; Gaub, B.; Martin, S.; Newton, R.; Beerli, C.; Mercer, J.; Gerber, C.; Müller, D.J. Inertial picobalance reveals fast mass fluctuations in mammalian cells. Nature 2017, 550, 500. [Google Scholar] [CrossRef] [PubMed]
- Reiche, C.F.; Körner, J.; Büchner, B.; Mühl, T. Introduction of a co-resonant detection concept for mechanical oscillation-based sensors. Nanotechnology 2015, 26, 335501. [Google Scholar] [CrossRef] [PubMed]
- Köerner, J. Effective sensor properties and sensitivity considerations of a dynamic co-resonantly coupled cantilever sensor. Beilstein J. Nanotechnol. 2018, 9, 2546–2560. [Google Scholar] [CrossRef] [PubMed]
- Rast, S.; Wattinger, C.; Gysin, U.; Meyer, E. Dynamics of damped cantilevers. Sci. Instrum. 2000, 71, 2772. [Google Scholar] [CrossRef]
- Giessibl, F.J.; Pielmeier, F.; Eguchi, T.; An, T.; Hasegawa, Y. Comparison of force sensors for atomic force microscopy based on quartz tuning forks and length-extensional resonators. Phys. Rev. B 2011, 84, 125409. [Google Scholar] [CrossRef]
- Körner, J.; Reiche, C.F.; Büchner, B.; Mühl, T.; Gerlach, G. Employing electro-mechanical analogies for co-resonantly coupled cantilever sensors. J. Sens. Sens. Syst. 2016, 5, 242. [Google Scholar] [CrossRef]
- Ilic, B.; Yang, Y.; Craighead, H.G. Virus detection using nanoelectromechanical devices. Appl. Phys. Lett. 2004, 85, 2604. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).