Contactless Readout of Passive LC Sensors with Compensation Circuit for Distance-Independent Measurements ^†

Abstract

Contactless readout of passive LC sensors composed of a capacitance sensor connected to a coil can be performed through an electromagnetically coupled readout coil set at distance d. Resonant frequency f_s and Q-factor Q_S of the LC sensor can be extracted from the measurement of the impedance at the readout coil by using a technique theoretically independent of d. This work investigates the effects on the measurement accuracy due to the unavoidable parasitic capacitance C_P in parallel to the readout coil, which makes the measured values of f_s and Q_S dependent on d. Numerical analysis and experimental tests confirm such dependence. To overcome this limitation, a novel electronic circuit topology for the compensation of C_P is proposed. The experimental results on assembled prototypes show that for a LC sensor with f_s ≈ 5.48 MHz a variation of less than 200 ppm across an interrogation distance between 2 and 18 mm is achieved with the proposed compensation circuit.

1. Introduction

Passive LC sensors can be obtained by connecting a capacitive sensor to a coil, thus forming a resonant LC circuit where the measurement information is related to the resonant frequency and the quality factor of the LC circuit. By magnetically coupling the coil connected to the sensor to an external interrogation coil, contactless readout of the LC-sensor can be achieved [1]. This configuration has recently gained particular interest in several fields such as industrial, chemical or biomedical applications. The lack of wired connection to the sensor is attractive in applications where cabled solutions are difficult or unpractical, such as measurement in sealed environments or inside animal/human bodies [1,2]. Additionally, these applications can take advantage on the absence of on-board power supply, allowing in principle for unattended unlimited operation. In-field measurement conditions are typically characterized by uncontrolled distance between the readout and the sensor coils, thus requiring interrogation techniques that desirably are independent of the distance between the coils. Approaches theoretically independent of the distance have been proposed both in the time-domain [3,4] and in the frequency-domain [2]. In the latter case, measuring the real part of the impedance at the readout coil allows to obtain the resonant frequency and the quality factor of the LC sensor [5,6]. The present work investigates on the limitations of such technique when considering unavoidable parasitic capacitances in parallel to the readout coil due to the connected electronics and cables. By means of numerical simulations and experimental tests, it has been demonstrated that the parasitic capacitances introduce dependence on the distance. As a solution, a circuit is proposed to compensate for this unwanted effect.

2. Operating Principle

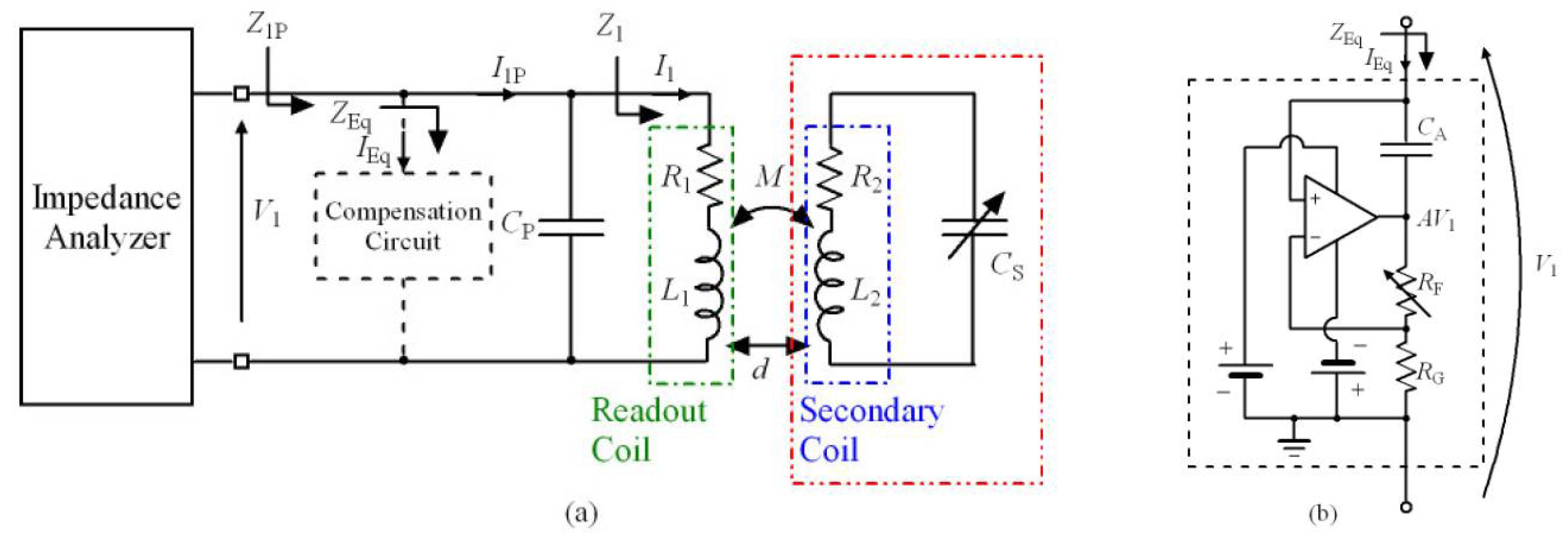
Figure 1a shows the schematic diagram of the proposed contactless readout system for capacitive sensors. It is composed of the interrogation unit made up by an impedance analyzer and the readout coil represented by inductance L1 and series resistance R1. The capacitance CP models the parasitic elements coming from the windings of the coil, cables, and any electronic circuits connected in parallel to the readout coil. The readout coil is magnetically coupled to the secondary coil represented by inductance L2 and series resistance R2. The magnetic coupling is described through the coupling factor k = ±M/(L1L2)^1/2, where the mutual inductance M is a parameter dependent on the interrogation distance d between the two coils, their geometries and orientation. The secondary coil and the connected capacitive sensor CS form a resonant LC circuit with resonant frequency fS and quality factor QS given by:

$$f_s=\frac{1}{\sqrt{L_2{C}_S}}, Q_s=\frac{1}{R_2}\sqrt{\frac{L_2}{C_S}}$$

(1)

In particular, when CP = 0 and without the compensation circuit, the sensor parameters f_S and Q_S can in principle be measured by considering the real part Re{Z₁} of the equivalent impedance Z₁ = V₁/I₁ through the readout coil, which results:

$$\mathrm{Re}\left\{Z_1\right\}=R_1+2\pi f_S{L}_1{k}^2{Q}_S\frac{{\left(f/f_S\right)}^2}{1+Q_S^2{\left(\frac{f}{f_S}-\frac{f_S}{f}\right)}^2}$$

(2)

From (2) it can be seen that k acts only as a scaling factor and both f_S and Q_S can be derived considering the frequency fm of the maximum of Re{Z₁} and the Full Width at Half Maximum (FWHM) bandwidth Δf_m trough the following relations [2]:

$$f_m=\frac{2Q_S}{\sqrt{4Q_S^2-2}}{f}_S, Q_S\approx \frac{f_S}{\Delta f_m}$$

(3)

From (3) it can be observed that for sufficiently large values of QS, it results fm ≈ fS, obtaining a relative deviation (fm – fS₎)/fS < 100 ppm for QS > 50. When CP ≠ 0 again, and without considering the compensation circuit, the real part of the impedance Z1_P = V1/I1_P = Z1//ZCP has the following more complex expression:

$$\mathrm{Re}\left\{Z_{1P}\right\}=\frac{\mathrm{Re}\left\{Z_1\right\}}{{\left(2\pi f{C}_P\mathrm{Re}\left\{Z_1\right\}\right)}^2+{\left(1-2\pi f{C}_P\mathrm{Im}\left\{Z_1\right\}\right)}^2}$$

(4)

From (3) and (4) it can be seen that now k does not act only as a scaling factor and without knowing its value in advance, it is not possible to extract fS and QS.

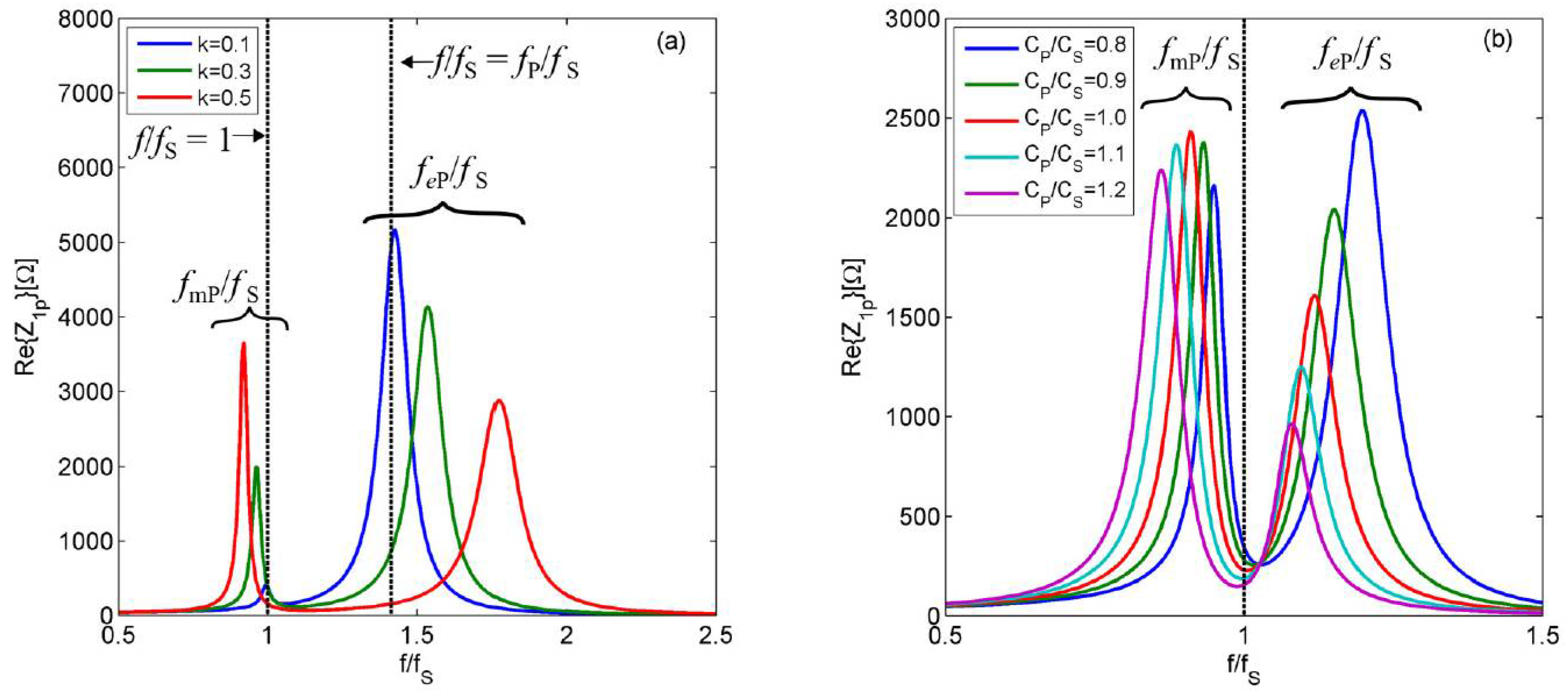
An analysis of the effects of k and CP on Re{Z1_P} has been performed numerically. Figure 2a shows Re{Z1_P} against f/fS, i.e., the frequency normalized to fS, for three different values of k when CP/CS = 0.5. The two vertical dotted lines are for f/fs = 1, i.e., corresponding to the resonant frequency of the LC sensor, and for f/fs = fP/fS, i.e., corresponding to the secondary resonant frequency fP = 1/(2π√(L1CP)) due to L1 resonating with CP. When CP ≠ 0, two peaks are present in Re{Z1_P}. Denoting with fmP/fS the position of the maxima close to f/fS = 1 and with feP/fS those close to fP/fS, it can be observed that for decreasing values of k, fmP/fS moves towards 1 and the associated peak value decreases, while feP/fS tends to fP/fS and the associated peak value increases, proving the distance-dependent behavior. For k = 0 there is no coupling between the readout coil and the sensor coil, and in that case, the height of the peak close to f/fS = 1 vanishes and only the peak at fP/fS can be measured. Figure 2b shows the effect of different values of CP/CS at fixed k = 0.2. From the results, it can be noticed that for increasing CP/CS, the ratio fmP/fS moves towards values lower than 1, while the ratio feP/fS tends to 1.

To avoid the dependence of fmP on CP and hence on the distance, the proposed compensation circuit of Figure 1b is connected in parallel to the readout coil. The circuit operates as a Negative Impedance Converter (NIC) providing the equivalent impedance ZEq = V1/IEq = 1/(j2πf(-CC)), where the negative capacitance −CC = −CARF/RG can be tuned through RF to compensate and possibly cancel CP.

3. Circuit Prototype and Experimental Results

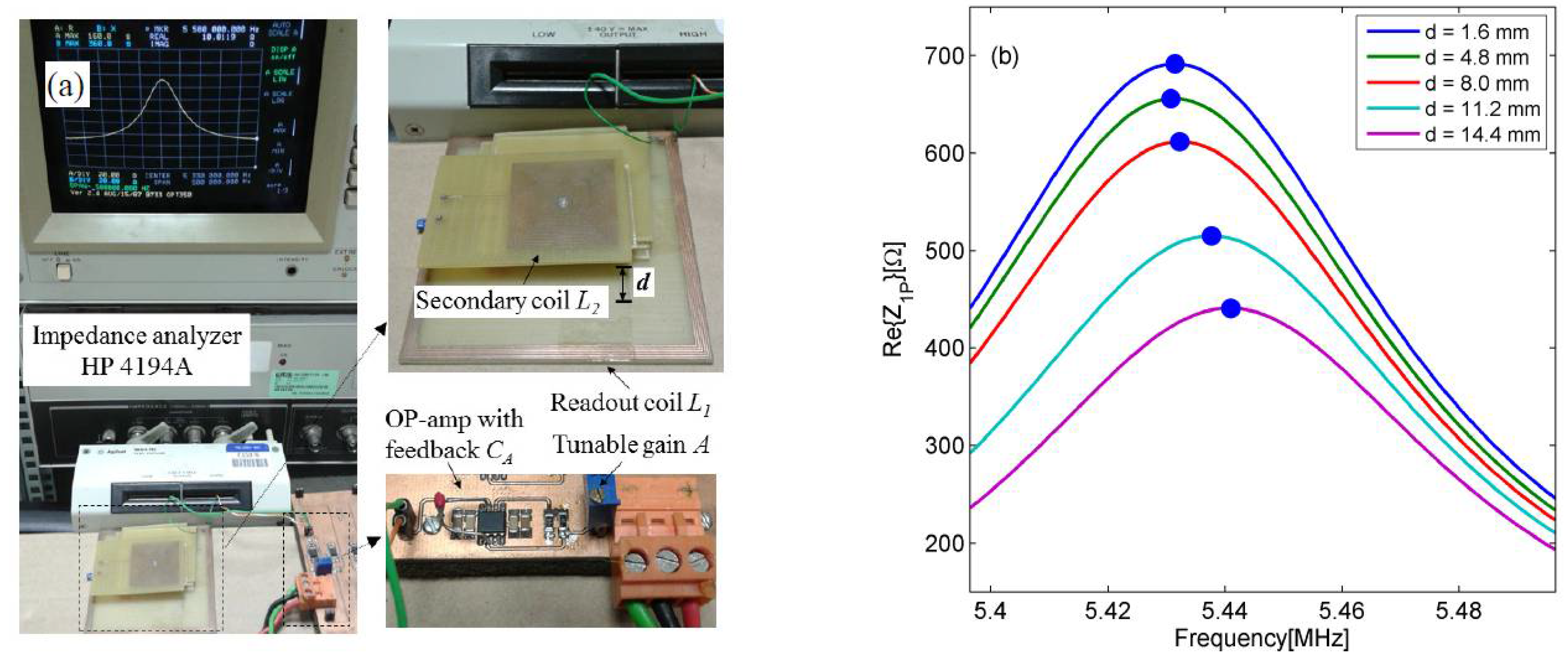
The compensation circuit of Figure 1b has been built by using a high-bandwidth operational amplifier (AD8045). Figure 3a shows the prototype and the experimental setup adopted to validate the proposed technique. The measured equivalent parameters for the readout and sensor coils are L1 = 8.17 µH and R1 = 3.12 Ω, and L2 = 8.50 µH and R2 = 3.20 Ω respectively. For the capacitive sensor, a capacitance CS = 99 pF has been adopted which from (1) gives for the LC resonant circuit fS = 5.48 MHz and QS = 91.5.

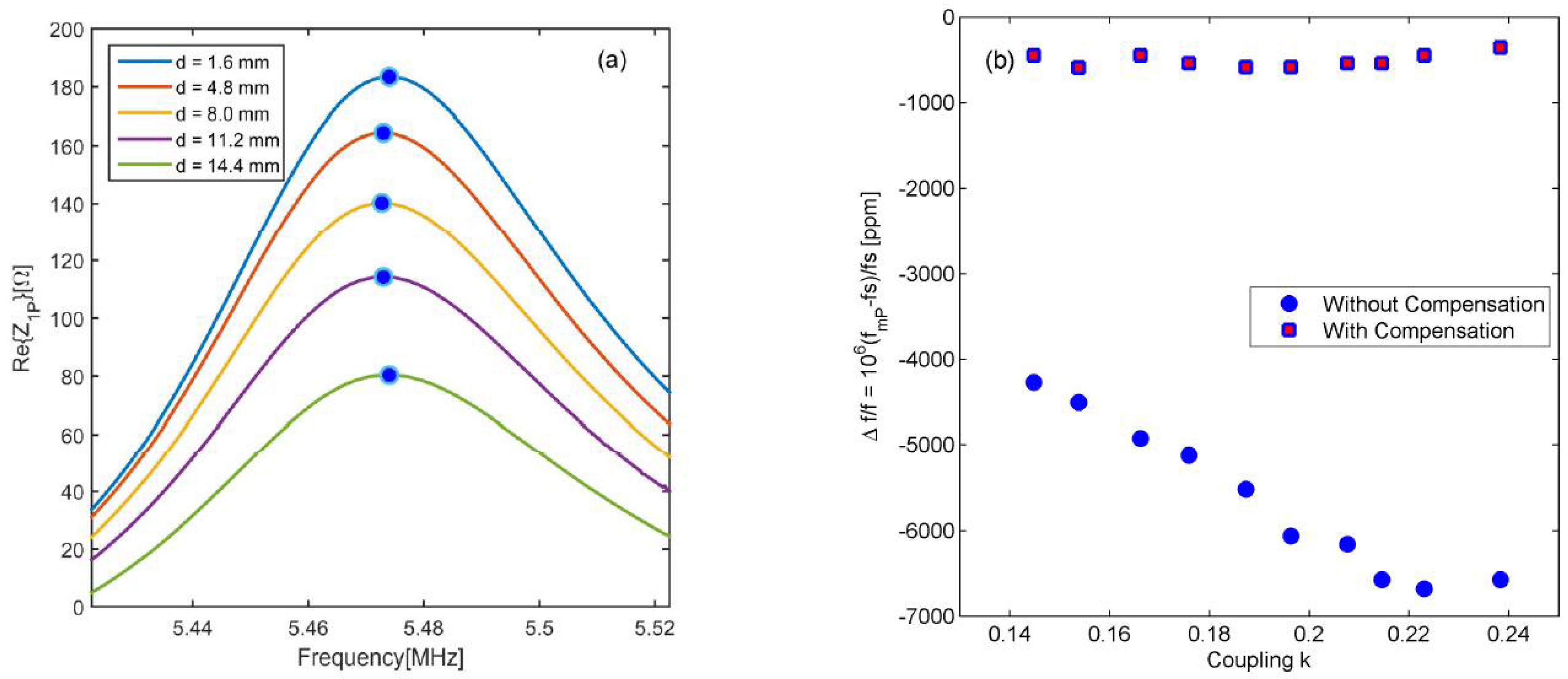
To validate the numerical analysis of Section 2, Figure 3b shows the measured Re{Z1_P} around fS at five different distances when a total parasitic capacitance of CP = 47 pF is present. It can be observed that, in agreement with the predictions of Figure 2a, the frequency of the maximum of Re{Z1_P} shifts towards higher frequencies for increasing distances, i.e., for decreasing values of k. Figure 4a shows the results of the same test with the compensation circuit tuned for the cancellation of CP activated. Figure 4b compares the cases of Figure 3b and Figure 4a, showing the relative frequency deviation Δf/f = 10⁶(fmP − fS)/fS as a function of the estimated coupling factor k. With the compensation circuit connected, a maximum relative deviation Δf/f less than 200 ppm is achieved.

4. Conclusions

The effect of a parasitic capacitance in parallel to the readout coil for contactless measurement of LC passive sensors has been investigated. Numerical analyses and experimental tests show that the parasitic capacitance introduces a dependence of the measured resonant frequency on the interrogation distance. A capacitance compensation circuit is proposed and validated to counteract the effect of the parasitic capacitance, outperforming equivalent systems based on the impedance phase-dip measurement proposed in the literature.