Vibration Mode Investigation of Piezoelectric Ultrasonic Microsensors on Buckled Diaphragms ^†

Abstract

Vibration mode of piezoelectric ultrasonic microsensors was investigated on buckled diaphragm structures from the viewpoint of higher order vibration modes than the fundamental one. Several vibration modes were generated on the diaphragms as the response to an ultrasound pulse, and their natural frequencies changed with increasing the buckling deflection in different rates. The natural frequencies of some modes approached each other, and the modes were accordingly superposed and degraded into a single mode in the large buckling ranges. The large buckling of the diaphragms consequently improves their vibration and thus the output waveforms.

1. Introduction

Piezoelectric ultrasonic microsensors have been fabricated on thin diaphragm structures. Figure 1 illustrates an example of the sensor structure with the piezoelectric diaphragm. Since the static deflection of the diaphragm structure enhances the mechano-electric energy conversion efficiency in vibration [1], the diaphragms were fabricated to have a static deflection by buckling due to the stress of the thermally oxidized silicon. The vibrating piezoelectric diaphragm has an in-homogeneous polarization distribution [2], and the top electrode of the sensor is designed to avoid cancellation of the positive and negative charges in the fundamental vibration mode [3]. A short pulse or burst waveform for ultrasonic measurement, however, has a wide frequency range far beyond the fundamental one, resulting in undesired interference by higher order vibrations. In the phased array ultrasonic measurement, the output signal from the sensors are synthesized by delay and summation [4], and the interference between the sensors detrimentally affects the measurement [5]. In this work, the vibration modes of the piezoelectric diaphragms with various buckling deflections were evaluated and the influence of the buckling to the vibration was investigated.

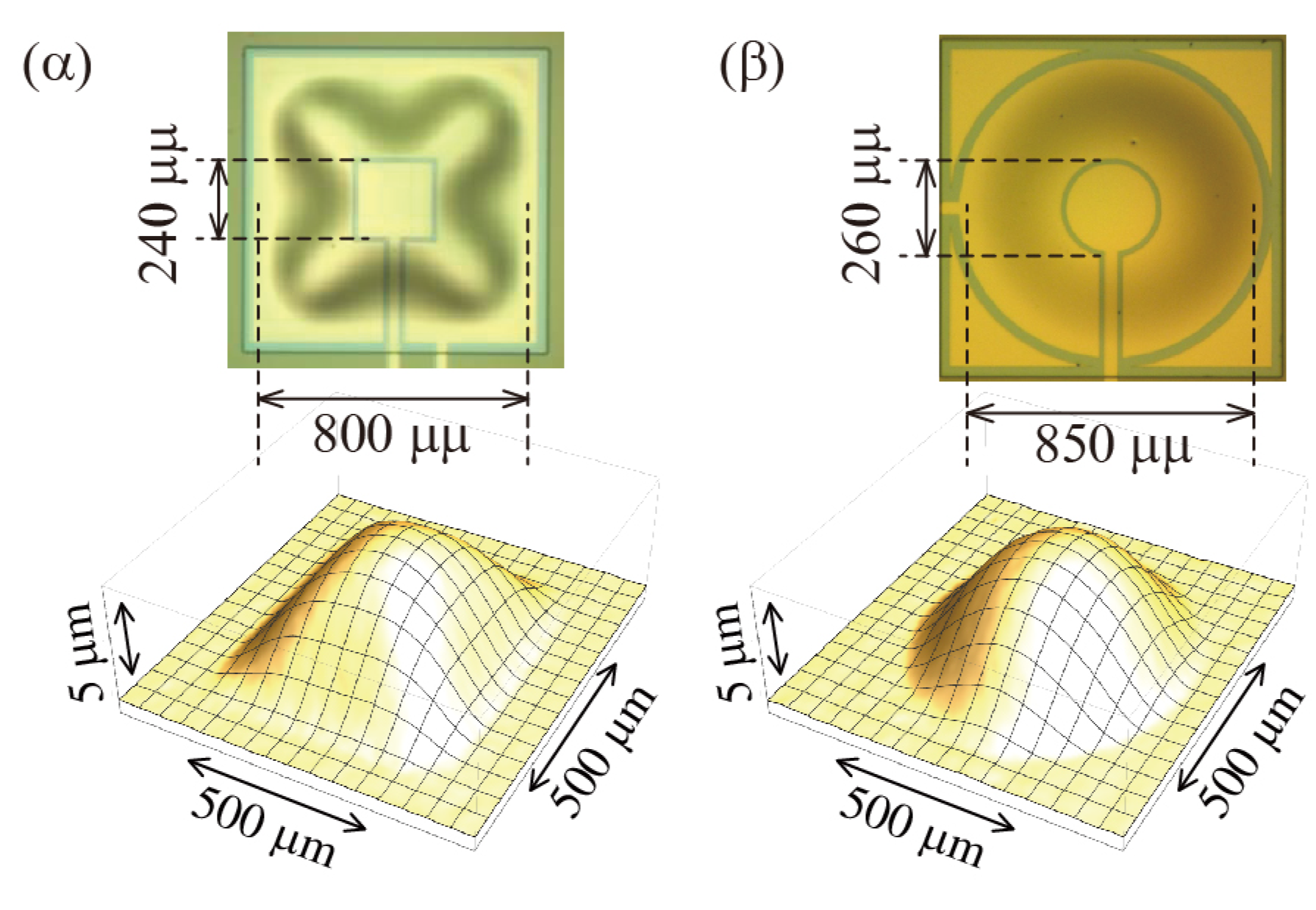
2. Experiments

The diaphragms having the buckling deflection in the range between 1.5 to 13 µm were fabricated. The buckling deflection was controlled by the stress of piezoelectric PZT film through its sol-gel preparation conditions [6]. Typical examples of fabricated square and circular diaphragm sensors are shown in Figure 2, as their top-view photographs and three-dimensional profiles measured by using optical profiler (Keyence, LT-9000, Osaka, Japan). A short ultrasound pulse was generated using electrical discharge and applied to the diaphragm sensors. Mechanical vibration of the diaphragm was measured by using laser Doppler vibrometer (Polytec Japan, MSV-400, Yokohama, Japan) and piezoelectric output waveform was obtained through a conventional amplifier (60 dB) and a storage oscilloscope (Yokogawa, DL850, Musashino, Japan). To evaluate the vibration modes in the transient response to the ultrasound pulse, the two-channel scanning vibrometry and velocity map synthesis technique was used [7]. We are interested in only centrosymmetric vibration modes because an anti-centrosymmetric vibration generates no piezoelectric output on the centrosymmetric top electrode. We evaluated the amount of contribution of each vibration mode by the vibration amplitude at the center of the diaphragm.

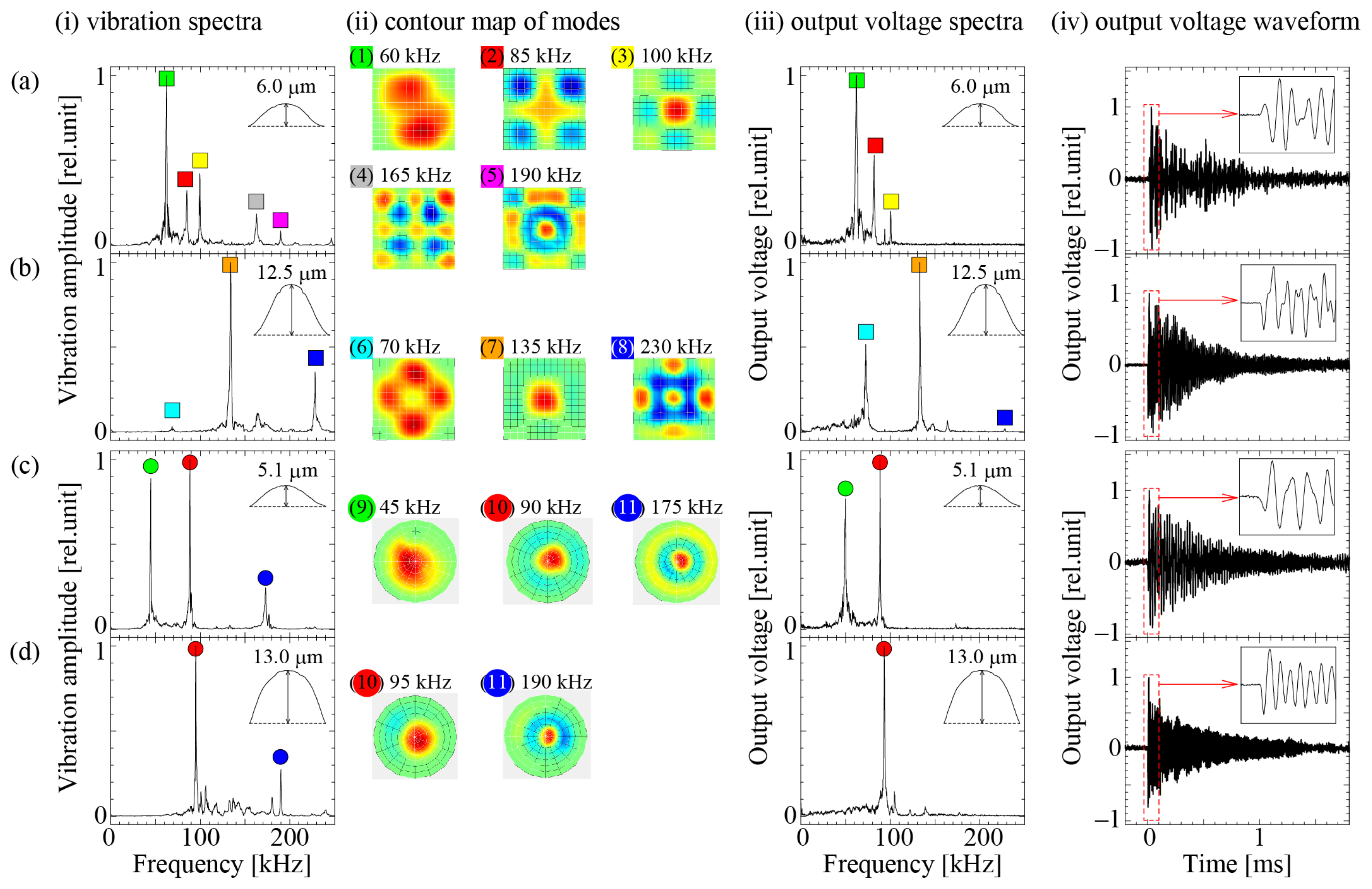
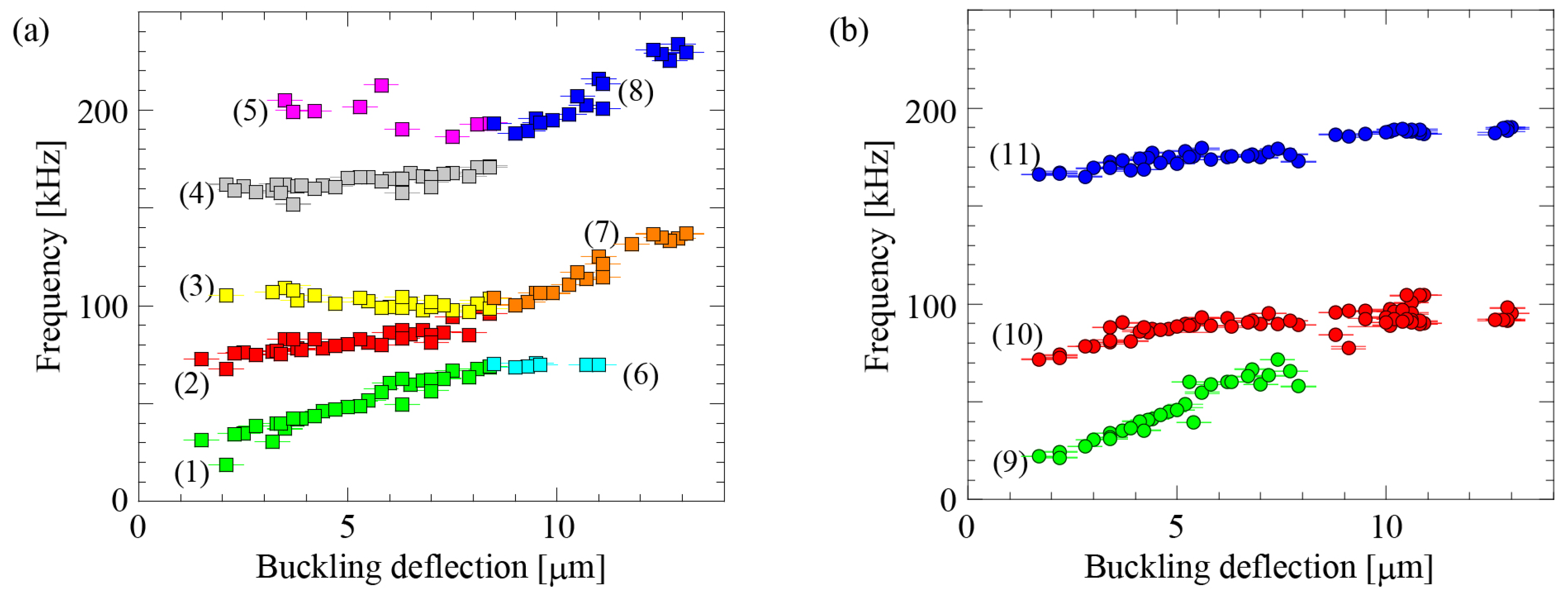
3. Results and Discussion

Figure 3 shows typical examples of the pulse responses of four sensors having square {(a), (b)} or circular {(c), (d)} diaphragms with small {(a), (c)} or large {(b), (d)} buckling deflections. The square diaphragms show larger number of spectral peaks than the circular diaphragms because complicated centrosymmetric modes can be easily induced on the square shape vibrator whereas only radial nodes can be easily induced on the circular shape vibrator. In a comparison of the buckling deflection, the diaphragms having larger deflection generates smaller number of vibration modes in both cases of the square and circular shapes. The piezoelectric responses have smaller number of spectral peaks than the vibration spectra because the high order vibration modes (4), (5), (8) and (11) have both the positive and negative curvature (i.e., polarization) in the top electrode region and no contribution to the output voltage. One exception: mode (6) has a small vibration amplitude at the center of the diaphragm but has a large curvature on the electrode, and thus has a non-negligible contribution to the piezoelectric output. The sensors having smaller number of output spectral peaks, in general, show less distorted damping oscillation in their time course waveforms of the piezoelectric output as shown in Figure 3 (iv), as distortion: (a) > (b) > (c) > (d).

Why the large buckling deflection reduces the number of vibration mode? Figure 4 shows the natural frequencies of the vibration modes versus the buckling deflection. Each vibration mode changes its natural frequency to the buckling deflection in its own rate, which is partially similar to that theoretically explained [8]. As the result, mode (1) changes to mode (6), modes (2) and (3) are superposed into mode (7), modes (4) and (5) are superposed into mode (8), and mode (9) disappears, around the deflection 8 µm. As shown in Figure 3 (ii), the modes (2) and (3) have the same vibration phase near the center of the diaphragm whereas opposite phases in the surrounding area, and thus the superposed mode (7) has a large vibration amplitude only in the central region, resulting in a much simpler vibration shape. The similar superposition is also observed in the case of modes (4) and (5) into (8). Figure 5 shows the relative intensity of the dominant vibration mode versus the buckling deflection. In the large deflection region over 8~10 µm, the relative intensity of the dominant vibration modes drastically increases, and the circular diaphragms having the deflection around 13 µm have almost a single vibration mode with nearly 100% contribution of the dominant mode.

4. Conclusions

Vibration mode and piezoelectric responses of ultrasonic microsensors were investigated on diaphragm structures, which were fabricated to have a buckling deflection for higher sensitivity. Influences of the buckling to the vibration were evaluated in laser Doppler vibrometry and in their piezoelectric responses to a short ultrasound pulse. Several vibration modes were generated on the diaphragms and their natural frequencies changed with increasing the buckling deflection in different rates. Natural frequencies of some modes approached each other in large buckling deflection ranges, and thus the vibration modes were superposed and degraded into a single mode, resulting in a much simpler vibration spectrum than that of the diaphragms having smaller buckling deflections. The results indicate that the diaphragm buckling is useful not only to enhance the sensitivity but also to improve the vibration of the diaphragm resulting in improved output signal waveforms.